
PGA Salad
"Geometric Algebra for Computer Graphics" SIGGRAPH Course Video + Resources

(PG)A: The Prequel
Being a gentle introduction to projective geometry
focusing on the parts that you need to grok PGA
Q: Why am I only learning about this now?
Q: Why am I only learning about this now?
Q: Why am I only learning about this now?
PGA
= P(GA)
= (PG)A
By associativity:

Masaccio 1420 Florence

Ideal elements in the plane

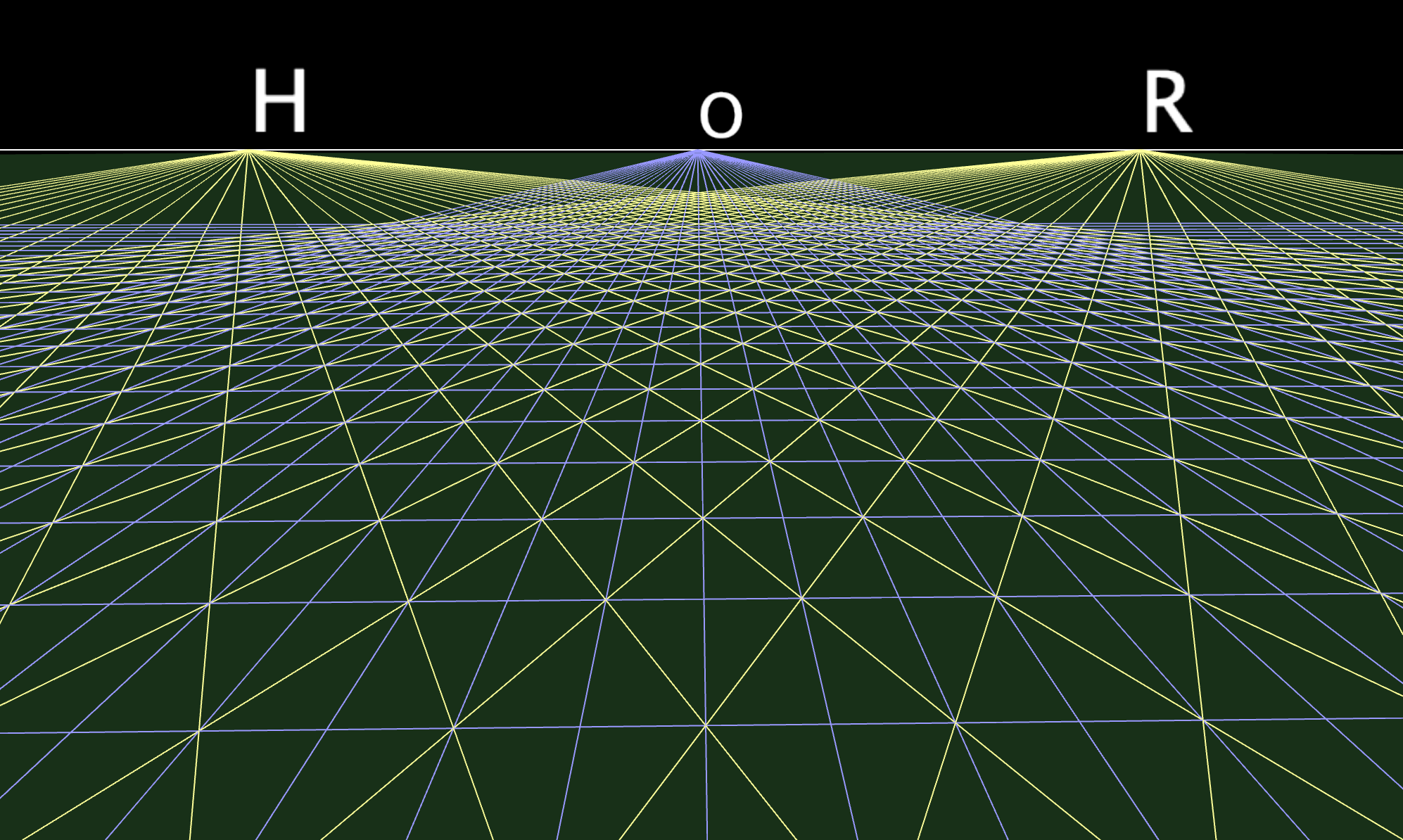
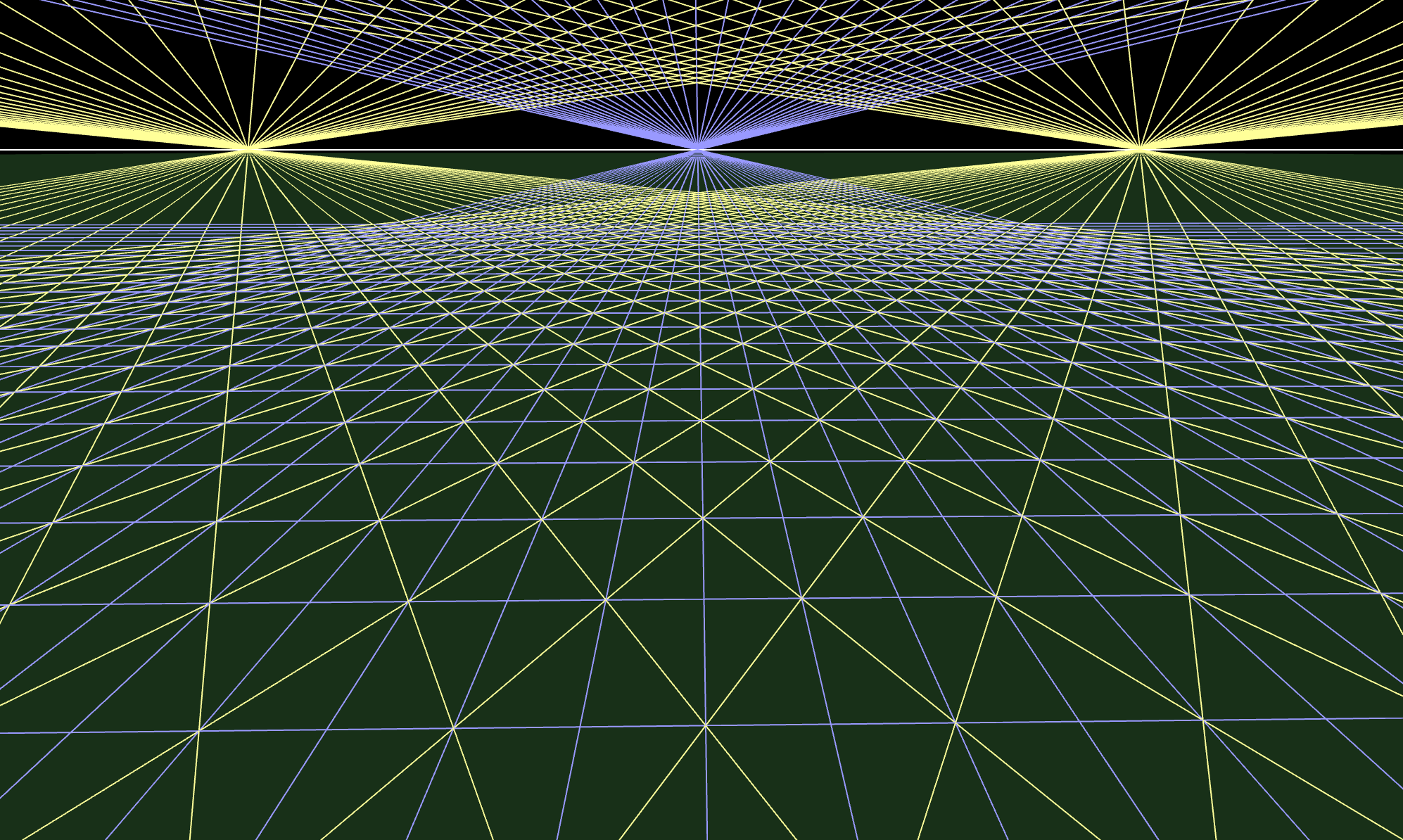
Euclidean vs. Projective geometry

Touch

Henry I (1100-1135) decreed the lawful yard to be the distance between the tip of his nose and the end of his thumb.
Euclidean vs. Projective geometry

Sight




Ideal vs. infinite
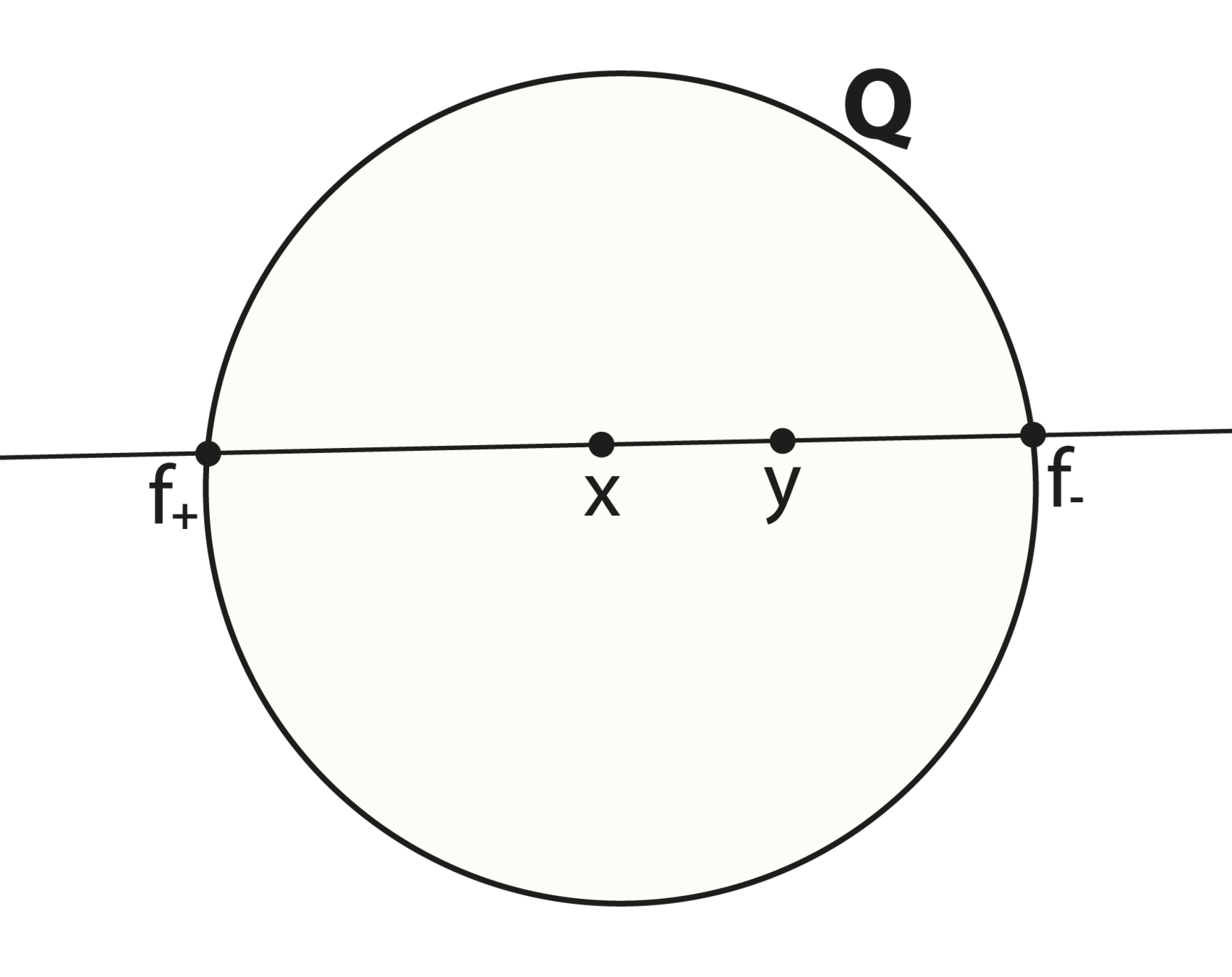
Example of sight vs. touch
Two parallel lines intersect in exactly one ideal point.

Example of sight vs. touch
Two parallel lines intersect in exactly one ideal point.

\(\bf{E^n}+\mathbb{R}P^{n-1}=\mathbb{R}P^{n}\)
\(\mathbb{R}P^0 =\infty\)
\(\bf{E^1}+\mathbb{R}P^{0}=\mathbb{R}P^{1}\)
\(...\)
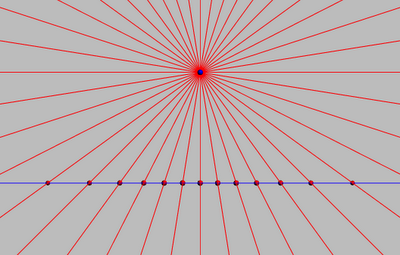
The lines passing through \(P\) are in 1:1 relation to the points of \(m\):
\(P \barwedge m\)
P
m
Perfect partnerships
Here four perspectivities are chained together to create a projectivity \(\Pi\):
\[\Pi: \ell \in P \rightarrow \\ \ell \barwedge m \barwedge Q \barwedge n \barwedge R\]
The points \(\ell \wedge \Pi(\ell)\) form a conic section, shown in black.
You can drag the points.
Perfect partnerships
(Im)Perfect partnerships
\[ax+by+c=0 ~~~(*)\]
For fixed \((a,b,c)\) this is a line equation: the set of all points \((x,y)\) satisfying (*) all lie on this line.
We call \((a,b,c)\) the homogeneous coordinates of the line.
For fixed \((x,y)\) this is a point equation: the set of all lines \((a,b,c)\) satisfying (*) all pass through this point.
We call \((x,y)\) the coordinates of the point.
Can you spot the missing elements?
\[ax+by+cz=0 ~~~(**)\]
For fixed \((a,b,c)\) this is a line equation: the set of all points \((x,y)\) satisfying (**) all lie on this line.
We call \((a,b,c)\) the homogeneous coordinates of the line.
For fixed \((x,y,z)\) this is a point equation: the set of all lines \((a,b,c)\) satisfying (**) all pass through this point.
We call \((x,y,z)\) the homogeneous coordinates of the point.
Now we can get ideal points and line!
(Im)Perfect partnerships
2D Dictionary of duality
point
intersect
lie on
move along
segment
triangle
line
join
pass through
rotate around
fan
trilateral
A line segment is the set of all points that are traversed when a point moves along a line from one point to another.
Two points determine two disjoint segments depending on which direction the point moves.
A point fan is the set of all lines that are traversed when a line rotates around a point from one line to another.
Two lines determine two disjoint fans depending on which direction the line rotates.
2D Duality Example: segment and fan
A line segment is the set of all points that are traversed when a point moves along a line from one point to another.
Two points determine two disjoint segments depending on which direction the point moves.
A point fan is the set of all lines that are traversed when a line rotates around a point from one line to another.
Two lines determine two disjoint fans depending on which direction the line rotates.
The "other" segment and fan
A triangle is determined by three points, its vertices. The pair-wise joining lines of the vertices are the sides of the triangle.
A trilateral is determined by three lines, its sides. The pairwise intersection points of the sides are the vertices of the trilateral.
2D Duality Example: triangle and trilateral
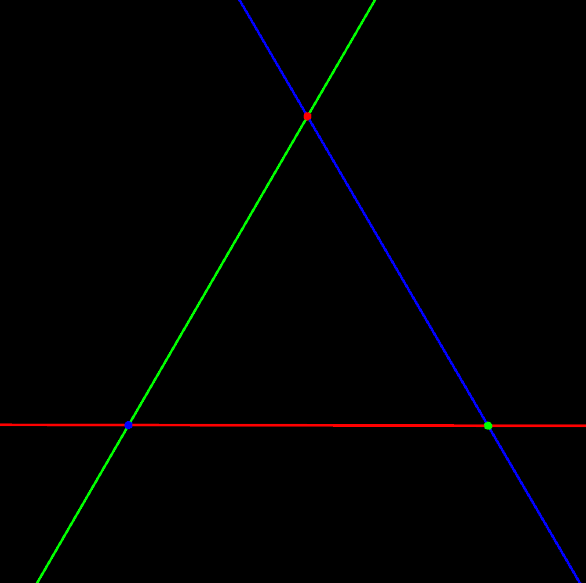

This is a self-dual configuration.
To traverse the boundary of the triangle, move a point from one vertex to the next vertex along their common side, then shift over and continue moving along the next side. Continue until arriving back at the original vertex.
To traverse the boundary of the trilateral, rotate a line from one side to the next around their common vertex, then shift over and continue rotating round the next vertex. Continue until arriving back at the original side.
2D Duality Example: triangle and trilateral
The center of gravity of a triangle is the average of its vertices ... A point is said to be inside the triangle if ... etc.
The center of levity of a trilateral is the average of its edges ... A line is said to be inside the trilateral if ... etc.
Triangle and trilateral: Further Extensions
Axioms of 3D projective geometry
- Two points are joined by a unique line.
- Three non-collinear points are joined by a unique plane.
- Two lines lying in a plane intersect in a unique point.
- ...
- Two planes intersect in a unique line.
- Three non-collinear planes intersect in a unique point.
- Two lines passing through a point are joined by a unique plane.
- ...
Perfect partnerships
The 3+7 basic forms of \(\mathbb{R}P^3\)
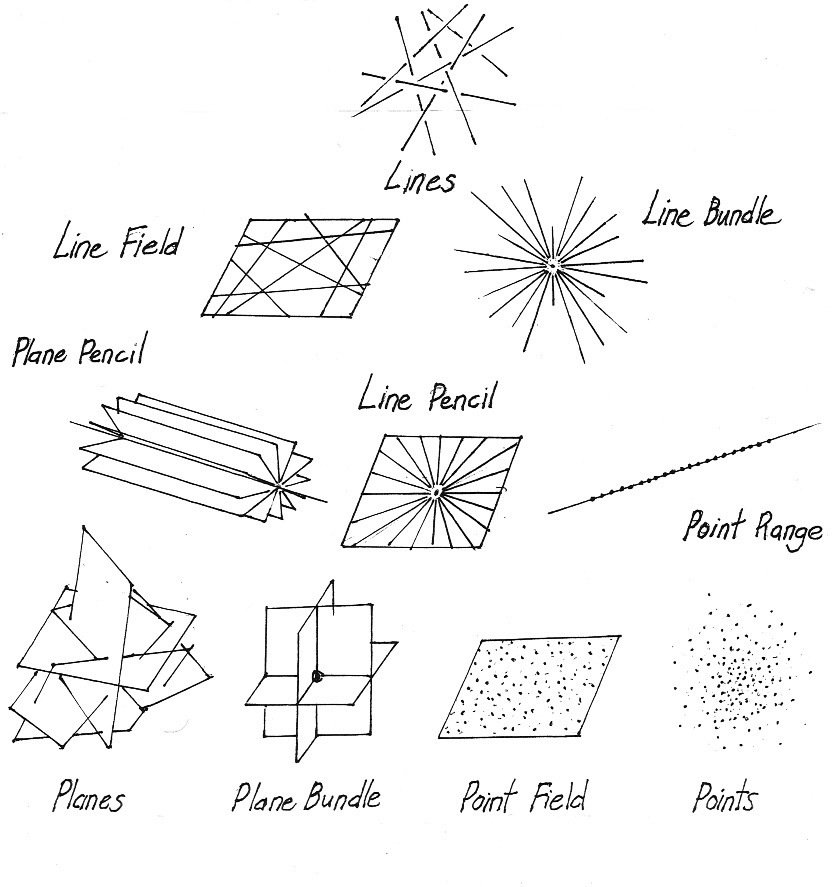
Start with the 3 basic spaces on the corners: points, lines, planes.
Drop an element from one space into another space and mark the incident elements.
This produces the six forms on the edges.
The line pencil arises from an incident point/plane pair dropped into line space.
3D Dictionary of duality
point
line of points (spear)
intersect
lie on
move along
segment
vertex
edge
plane bundle
line bundle
point range
plane
line of planes (axis)
join
pass through
rotate around
fan
face
edge
point field
line field
plane pencil
3D duality example
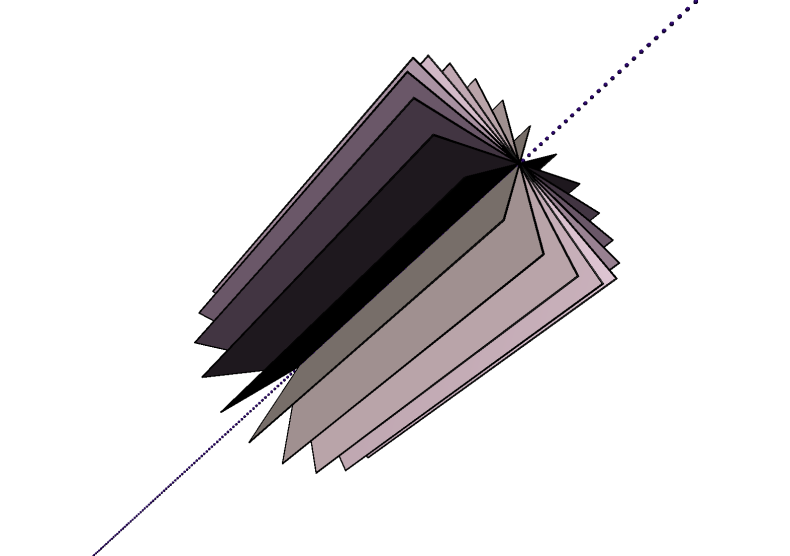
spear
axis
A velocity state in euclidean kinematics is an axis
A momentum/force state in euclidean dynamics is a spear.
Riddle: When is a line not a line?
Answer: When its a spear or an axis.
Cube and octahedron



The three joining lines of opposite vertices of the octahedron pass through the center point of the octahedron.
The three ______ ______ of opposite ______ of the cube _____ the center ______ of the cube.
Exercise
Fill in the blanks on the right.
Forward link: Counting subspace dimensions
In PGA, 1-vectors are
0-dimensional
indivisible
simple
whether they are point or plane.
The wedge operator \(\wedge\) determines how the world constructed.
| grade | standard GA | dual GA |
|---|---|---|
| 1 | point | plane |
| 2 | point range | plane pencil |
| 3 | point field | plane bundle |
The cross ratio: a projective invariant
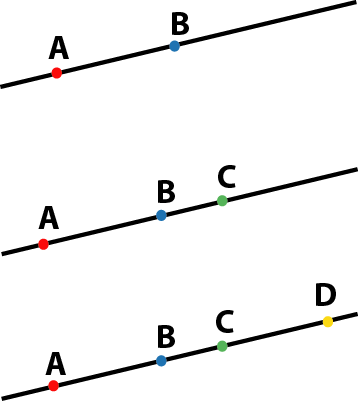
Metric geometry:
the distance \(AB\) is invariant.
Metric+uniform scaling:
the ratio \(\frac{AC}{AB}\) is invariant.
Projective geometry:
the double ratio \(\frac{AC}{AB}:\frac{DC}{DB}\) is invariant, also called cross ratio.
Harmonic points: cross ratio = -1
For further study
Being a gentle introduction to non-euclidean geometry and how spherical, hyperbolic, and euclidean geometries are all
PGA: Equal
*
*
equal
citizens in PGA.
Noneuclidean (metric) geometry
1820: Proving the parallel postulate.
Given a line and a point not on the line there exists exactly one line through the point parallel to the line.
Noneuclidean (metric) geometry
Euclid's fifth postulate can't be proved.
There are three possibilities.
| Name | Elliptic | Euclidean | Hyperbolic |
|---|---|---|---|
| # parallels | 0 | 1 | 2 |
| sum of angles | >180 | =180 | <180 |
| curvature | +1 | 0 | -1 |



Noneuclidean (metric) geometry



236
euclidean
235
elliptic
237
hyperbolic
The three triangle groups
3D: Three regular pentagon dodecahedra
euclidean
\(\alpha = 116.57^\circ\)
elliptic
\(\alpha = \frac{2\pi}{3}=120^\circ\)
hyperbolic
\(\alpha = \frac{\pi}{2}=90^\circ\)


Why learn about noneuclidean geometry?
- It's cool!
- Elliptic geometry \(\cong \frac12\) spherical geometry.
- Google: "hyperbolic geometric graph".
- "Almost all" 3-dimensional topological manifolds are hyperbolic. Poincare conjecture, Thurston's geometrization program, "Not Knot".
- Euclidean geometry is a limiting case of noneuclidean geometries.
"Not Knot" (Geometry Center, 1992)
Cayley-Klein geometry:
Metric geometry inside
projective geometry


"Projective geometry is all geometry."
Arthur Cayley (1821-1895)
Cayley-Klein geometry:
Metric geometry inside projective geometry


| Name | elliptic | euclidean | hyperbolic |
|---|---|---|---|
| signature | (3,0,0) | (2,0,1) | (2,1,0) |
| null points | |||
| null lines |
\(x^2+y^2+z^2\)=0
\(x^2+y^2-z^2\)=0
Cayley-Klein geometries for n = 2



\(a^2+b^2+c^2\)=0
\(x^2+y^2-z^2\)=0
\(a^2+b^2-c^2\)=0
\(a^2+b^2\)=0
\(z^2\)=0
PGA for Cayley-Klein spaces
\(P(\mathbb{R}^*_{n,1,0})\) or \(P(\mathbb{R}_{n,1,0})\): hyperbolic n-space
\(P(\mathbb{R}^*_{n+1,0,0})\) or \(P(\mathbb{R}_{n+1,0,0})\): elliptic n-space
We use the noneuclidean dual models since we want to generate the motion group using reflections in planes, not points.
The noneuclidean dual and standard algebras are equivalent since the metric is non-degenerate, i. e., \(\bf{X} \Rightarrow \bf{X}\bf{I}\) is an isomorphism.
\(P(\mathbb{R}^*_{n,0,1})\): euclidean n-space
\(P(\mathbb{R}_{n,0,1})\): dual euclidean n-space
PGA: multiplication by \(\bf{I}\)
Multiplication with \(\mathbf{I}\): For any k-vector \(\mathbf{x}\), \(\mathbf{x}^\perp := \mathbf{x}\mathbf{I}\) is the orthogonal complement of \(\mathbf{x}\).
This map is called the polarity on the metric quadric.
Example: \(\mathbf{e}_0 \mathbf{I} = \kappa\mathbf{e}_1\mathbf{e}_2\). The only thing left in \(\mathbf{I}\) is what isn't in \(\mathbf{X}\).
In noneuclidean PGA, multiplication by \(\bf{I}\) is a perfect partnership. Every element has a unique complement.
Appllied to the whole algebra, you obtain another geometry with the same signature.
But in euclidean and dual euclidean, NOT. Multiplying by \(I\) in the euclidean PGA collapses onto the ideal plane \(\bf{e}_0\).
Metric-neutral point and line calculations
\(\ell\) = line (vector)
\(P\) = point (bivector)
\(\ell P\) = line through \(P, \perp\) to \(\ell\)
\(\ell P\ell\) = reflection of \(P\) in \(\ell\)
\(P\ell P\) = reflection of \(\ell\) in \(P\)
\((\ell \cdot P)\ell\) = projection of \(P\) on \(\ell\)
\((P \cdot \ell)P\) = projection of \(\ell\) on \(P\)
Metric-neutral point and line calculations
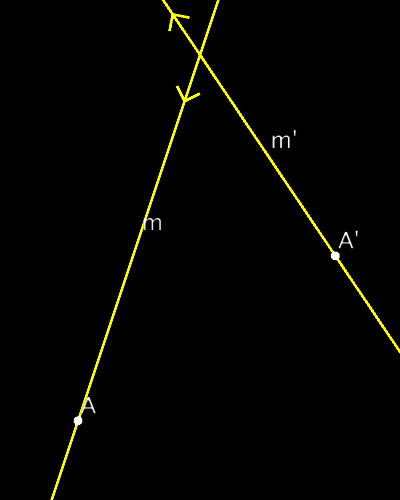
Metric-neutral 2D PGA example
//Main idea: "rotation" center has to lie on
//perpendicular bisector of AA' AND
// on angle bisector of mm'
// Find intersection of m and m2 and
// line through a and a2
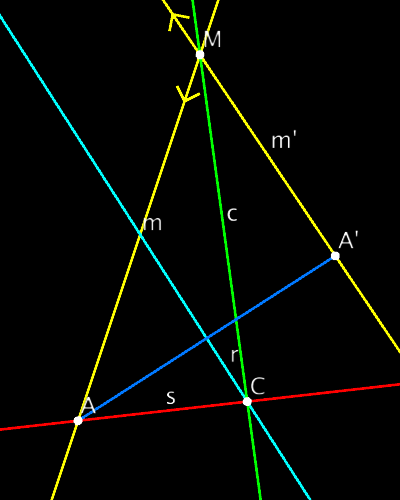
M=()=>(m^m2), a=()=>join(A,A2),
// Find the midpoint between A and A2 and the
// orthogonal line through it (| is inn. prod.)
Am=()=>(A+A2), r=()=>(a|Am),
// c is angle bisector of m and m2. Cut that
// with r to find the center point of isometry
c=()=>(m-m2), C=()=>(r^c),
// Construct the transformation as a "rotation"
// fixing C. (metric- and ideal-neutral)
s=()=>join(A,C), g=()=>(r*s),
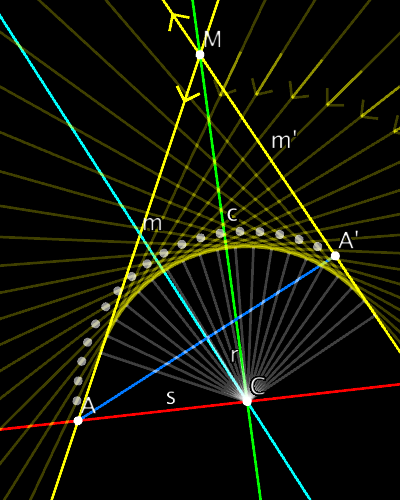
Metric neutral 2D PGA example
For further study
Charles Gunn, "Metric-neutral Visualization"
Charles Gunn, "Discrete groups and the visualization of 3-dimensional manifolds", SIGGRAPH 1993
Metric-neutral
rigid body mechanics
with PGA
Poinsot motion of the Euler top
Poinsot motion of the Euler top

The Euler top via PGA
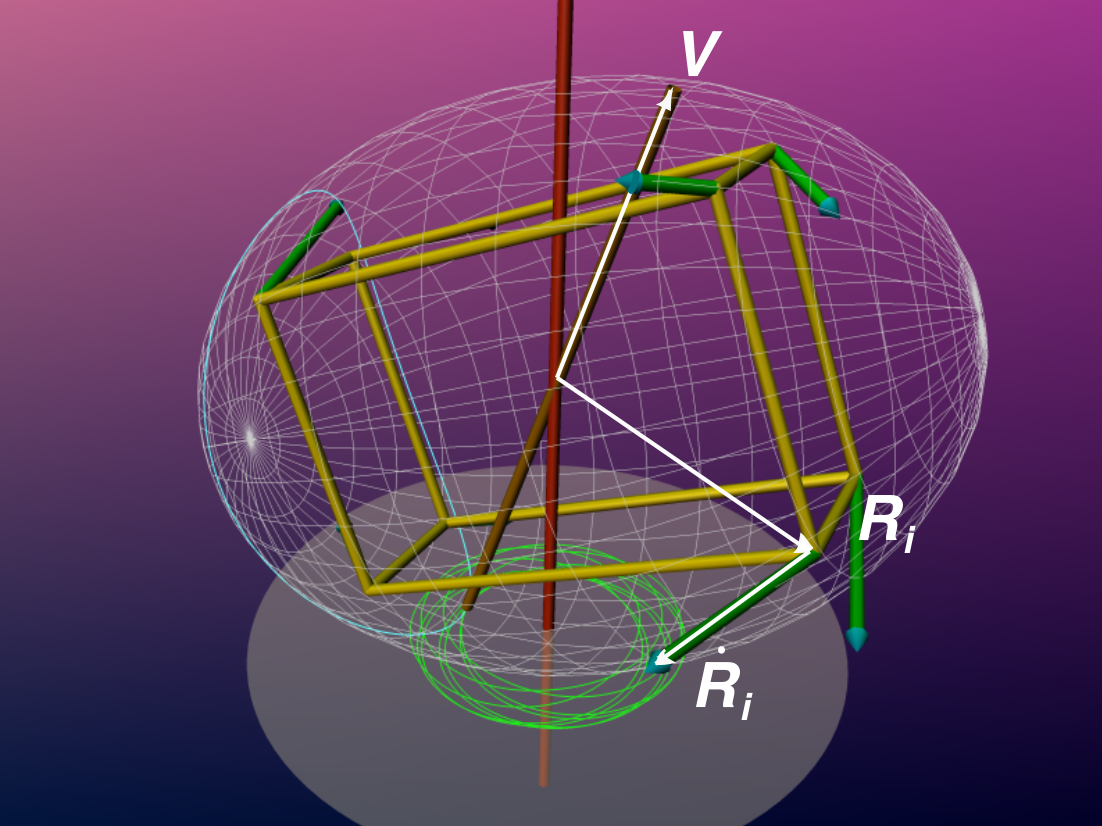
The global velocity state \(V\) is a line thru origin.
The velocity vector at R:
\[\dot{\bf{R}_i}=(\bf{R}_i\times \bf{V}) \] \[=(\bf{R}_i\vee \bf{V})\bf{I} \]
The momentum line:
\[\bf{M}_i := \dfrac{m_i}{2}(\dot{\bf{R}}_i \vee\bf{R}_i)\]
Kinetic energy of particle:
\[E_i = \bf{M}\vee\bf{V}\]
using inertia tensor:
\[E_i = A_i(\bf{V},\bf{V}) \]
\[\bf{M}_i = A_i(\bf{V},\circ) \]
*Note: \(\bf{X}\times\bf{Y} := \frac12 (\bf{X}\bf{Y} - \bf{Y}\bf{X})\)
The Euler top via PGA

Global momentum & energy
\[E := \sum_i E_i\]
\[ \bf{M} := \sum_i \bf{M}_i\]
\[ A := \sum_i A_i\]
\[ m := \sum_i m_i\]
Then by linearity:
\[ \bf{M} = A(\bf{V}, \circ)\]
\[E= \bf{M} \vee \bf{V}\]
Rigid body motion using 3D line geometry
The free top via PGA
All of the formulas derived for the Euler top remain true for the free top!
The only difference is that the velocity state \(\bf{V}\) can be any bivector (any arbitrary screw motion in space).
Also valid in any metric: behavior begins to be very different in the different metrics.
We look now at how the equations of motion look in PGA ...
Quaternion ODE's for Euler Top
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
Quaternion equations for the Euler top in \(\mathbb{R}^3\):
$$\dot{\mathbf{g}} = \mathbf{g} \mathbf{V}$$ $$ \dot{\mathbf{M}} = \frac12(\mathbf{V}\mathbf{M} - \mathbf{M} \mathbf{V}) $$
where \(\mathbf{g} \in \mathbb{U}\) and \(\mathbf{M}, \mathbf{V} \in \mathbb{IH}\) are the momentum, resp., velocity vectors in the body frame.
(\(\mathbf{M}={A}\mathbf{V}\) for inertia tensor \(A\)).
Metric-neutral Euler equations
for the free top in PGA
Given a rigid body with inertia tensor \(A\) under the influence of a global velocity state \(\bf{V}\).
Then the equations for the motion \(\bf{g}\) are given by the following ODE's:
\[\dot{\bf{g}} = \bf{g}\bf{V}_c\]
\[\dot{\bf{M}_c}=2(\bf{\bf{M}_c} \times \bf{V}_c) \]
where \(\bf {X_c}\) indicates use of body frame, \( \bf{\bf{M}_c} := A(\bf{\bf{V}_c})\) is the momentum state, and \(X \times Y := \frac12 (XY - YX)\) is the commutator product.
Noneuclidean rigid body motion
Advantages of PGA approach to kinematics and rigid body mechanics
It's metric-neutral.
In the euclidean case, it unifies many special cases:
It unifies linear and angular parts of momentum and velocity.
Force couples are forces carried by ideal lines.
Translations are "rotations" around ideal lines.
It also unifies many cases in the noneuclidean case too:-).
It has great numerical properties: 12D solution \(\subset\) 14D phase space
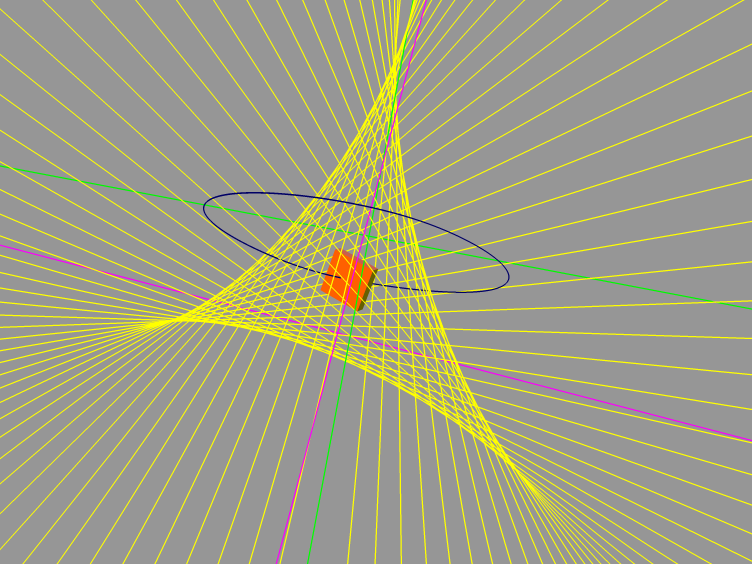


3D
Poinsot motion (?)
For further study
Charles Gunn, "Geometry, Kinematics, and Rigid Body Mechanics in Cayley-Klein Geometries", Ph. D. Thesis, 2011. On researchgate/charlesgunn
Looking to the future
PGA: Sequel
This section has been omitted due to its unfinished form.
It focused on novel applications of dual euclidean space.
For an introduction to previous work in this direction, see Ch. 10 of my Ph. D. thesis here.
If you would like to be notified when something more publishable of this new research is available, drop me a line at projgeom@gmail.com.
That's all folks