


My career in six pictures
1978: UNC-CH undergrad
hidden surface algorithm
mainframe + punch cards
1978: UNC-CH undergrad
Moebius band visualization
Vector display + PDP 11
1983: UNC-CH M. S. project
2D wallpaper groups
frame buffer + VAX
microcode assembler
1986: Pixar software developer
REYES software for "Red's Dream"
Pixar Image Computer
assembler
1992: Geometry Center, U MN
technical director "Not Knot"
SGI workstations
Geomview: 3D scene graph in C++
2003-15: TU-Berlin Math
software/movies/teaching
Macs
jReality: 3D scene graph in Java
1997-2003: high school teacher
no computers
study of projective geometry

HISTORICAL RE-ENACTMENT

2003
2010
"Geometric Algebra for Computer Graphics" SIGGRAPH Course Video + Resources

(PG)A: The Prequel
Being a gentle introduction to projective geometry
focusing on the parts that you need to grok PGA
Q: Why am I only learning about this now?
Q: Why am I only learning about this now?
Q: Why am I only learning about this now?
PGA
= P(GA)
= (PG)A
By associativity:

Masaccio 1420 Florence

Ideal elements in the plane

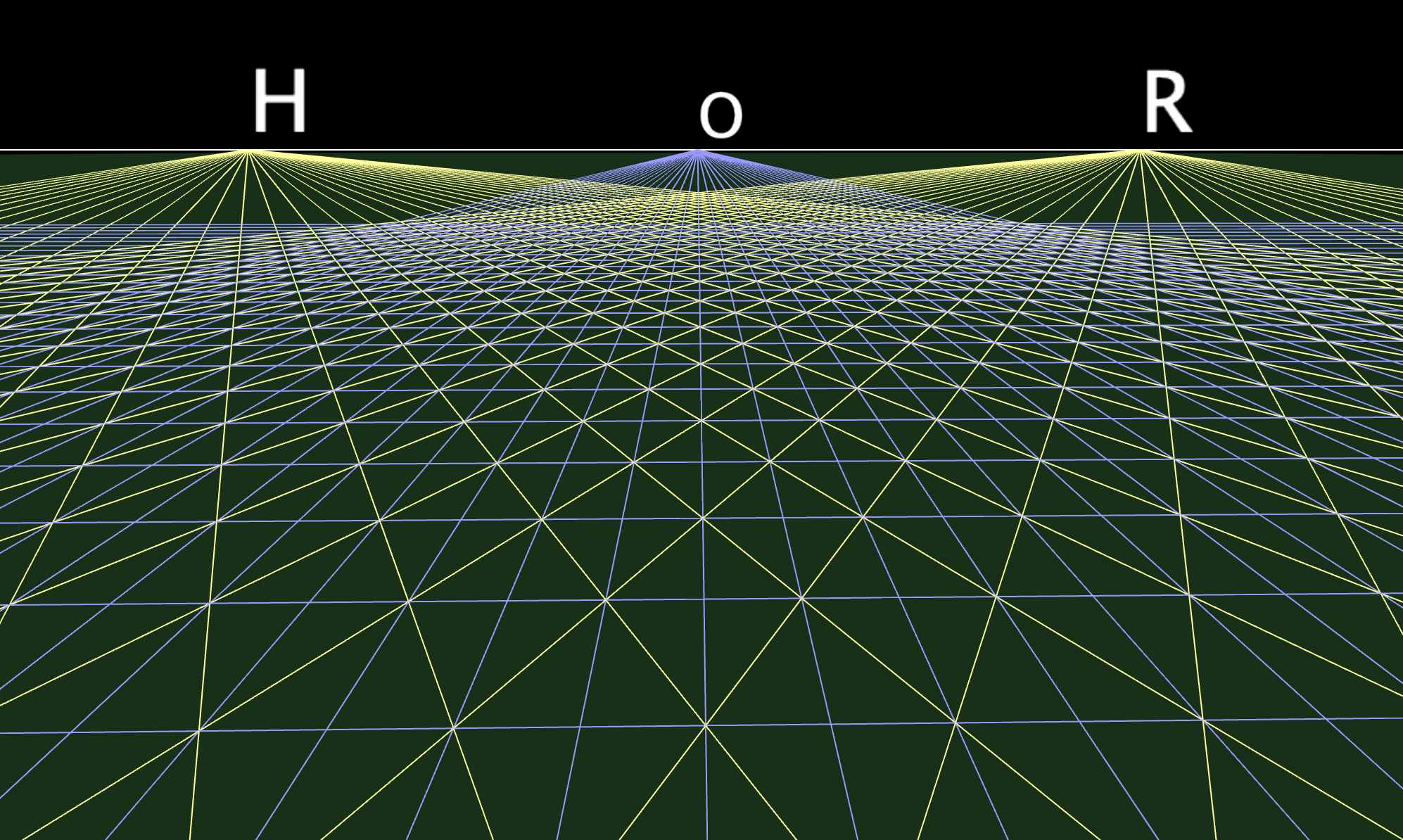
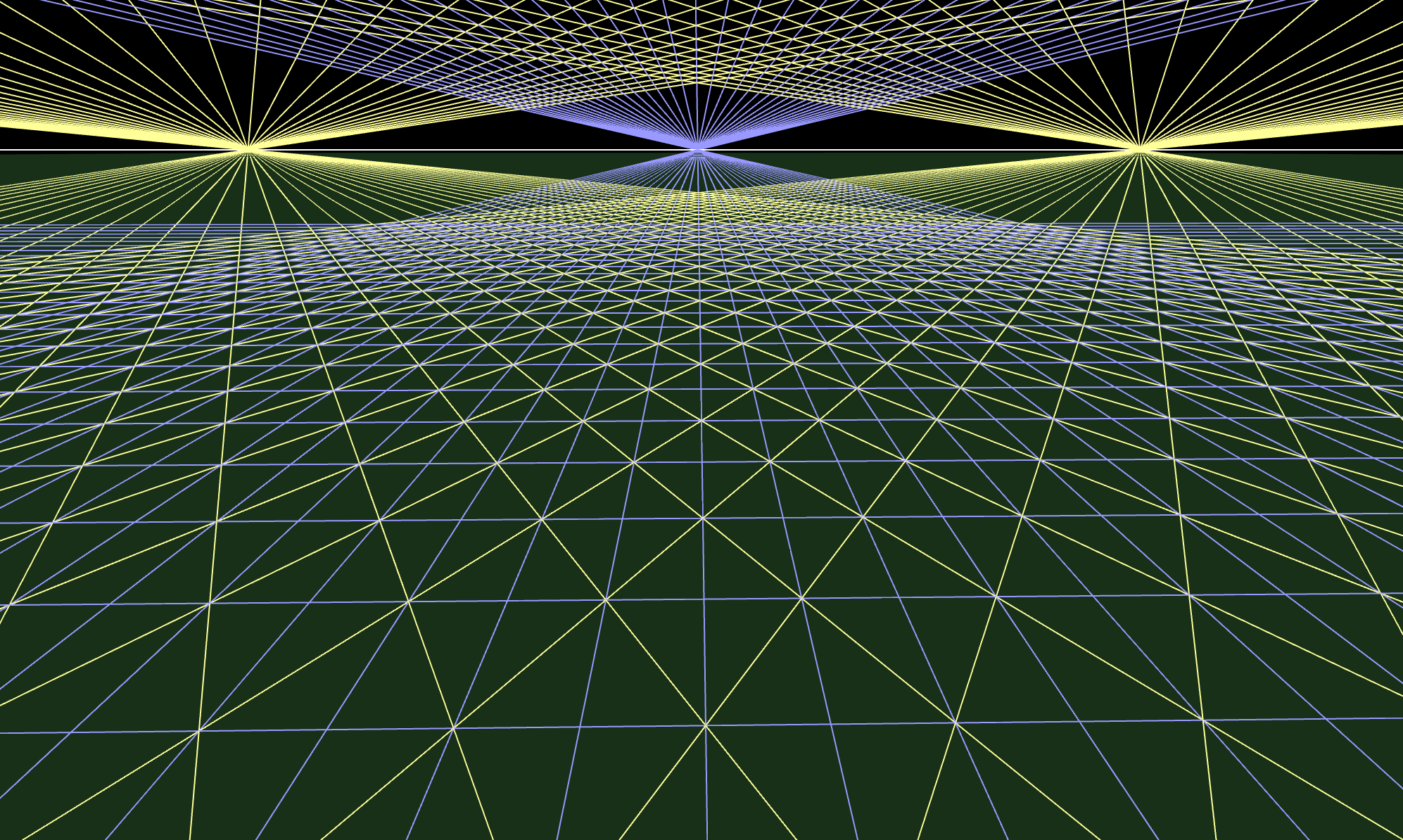
Euclidean vs. Projective geometry

Touch

Henry I (1100-1135) decreed the lawful yard to be the distance between the tip of his nose and the end of his thumb.
Euclidean vs. Projective geometry

Sight




Ideal vs. infinite
Example of sight vs. touch
Two parallel lines intersect in exactly one ideal point.

Example of sight vs. touch
Two parallel lines intersect in exactly one ideal point.

\(\bf{E^n}+\mathbb{R}P^{n-1}=\mathbb{R}P^{n}\)
\(\mathbb{R}P^0 =\infty\)
\(\bf{E^1}+\mathbb{R}P^{0}=\mathbb{R}P^{1}\)
\(...\)
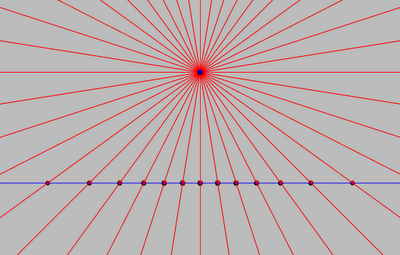
The lines passing through \(P\) are in 1:1 relation to the points of \(m\):
\(P \barwedge m\)
P
m
Perfect partnerships
Here four perspectivities are chained together to create a projectivity \(\Pi\):
\[\Pi: \ell \in P \rightarrow \\ \ell \barwedge m \barwedge Q \barwedge n \barwedge R\]
The points \(\ell \wedge \Pi(\ell)\) form a conic section, shown in black.
You can drag the points.
Perfect partnerships
(Im)Perfect partnerships
\[ax+by+c=0 ~~~(*)\]
For fixed \((a,b,c)\) this is a line equation: the set of all points \((x,y)\) satisfying (*) all lie on this line.
We call \((a,b,c)\) the homogeneous coordinates of the line.
For fixed \((x,y)\) this is a point equation: the set of all lines \((a,b,c)\) satisfying (*) all pass through this point.
We call \((x,y)\) the coordinates of the point.
Can you spot the missing elements?
\[ax+by+cz=0 ~~~(**)\]
For fixed \((a,b,c)\) this is a line equation: the set of all points \((x,y)\) satisfying (**) all lie on this line.
We call \((a,b,c)\) the homogeneous coordinates of the line.
For fixed \((x,y,z)\) this is a point equation: the set of all lines \((a,b,c)\) satisfying (**) all pass through this point.
We call \((x,y,z)\) the homogeneous coordinates of the point.
Now we can get ideal points and line!
(Im)Perfect partnerships
2D Dictionary of duality
point
intersect
lie on
move along
segment
triangle
line
join
pass through
rotate around
fan
trilateral
A line segment is the set of all points that are traversed when a point moves along a line from one point to another.
Two points determine two disjoint segments depending on which direction the point moves.
A point fan is the set of all lines that are traversed when a line rotates around a point from one line to another.
Two lines determine two disjoint fans depending on which direction the line rotates.
2D Duality Example: segment and fan
A line segment is the set of all points that are traversed when a point moves along a line from one point to another.
Two points determine two disjoint segments depending on which direction the point moves.
A point fan is the set of all lines that are traversed when a line rotates around a point from one line to another.
Two lines determine two disjoint fans depending on which direction the line rotates.
The "other" segment and fan
A triangle is determined by three points, its vertices. The pair-wise joining lines of the vertices are the sides of the triangle.
A trilateral is determined by three lines, its sides. The pairwise intersection points of the sides are the vertices of the trilateral.
2D Duality Example: triangle and trilateral
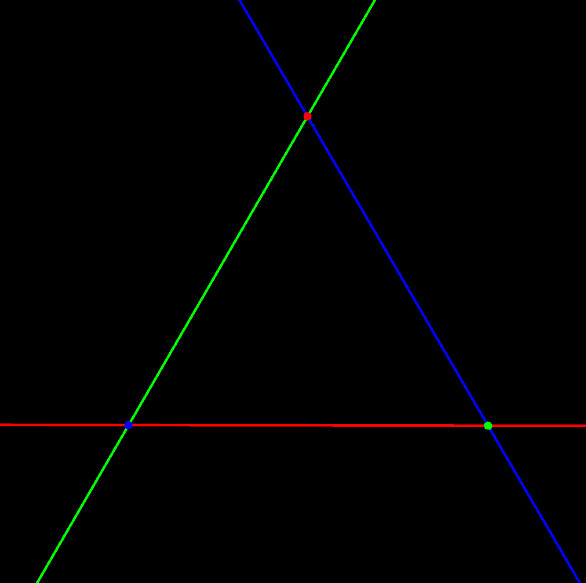

This is a self-dual configuration.
To traverse the boundary of the triangle, move a point from one vertex to the next vertex along their common side, then shift over and continue moving along the next side. Continue until arriving back at the original vertex.
To traverse the boundary of the trilateral, rotate a line from one side to the next around their common vertex, then shift over and continue rotating round the next vertex. Continue until arriving back at the original side.
2D Duality Example: triangle and trilateral
The center of gravity of a triangle is the average of its vertices ... A point is said to be inside the triangle if ... etc.
The center of levity of a trilateral is the average of its edges ... A line is said to be inside the trilateral if ... etc.
Triangle and trilateral: Further Extensions
Axioms of 3D projective geometry
- Two points are joined by a unique line.
- Three non-collinear points are joined by a unique plane.
- Two lines lying in a plane intersect in a unique point.
- ...
- Two planes intersect in a unique line.
- Three non-collinear planes intersect in a unique point.
- Two lines passing through a point are joined by a unique plane.
- ...
Perfect partnerships
The 3+7 basic forms of \(\mathbb{R}P^3\)
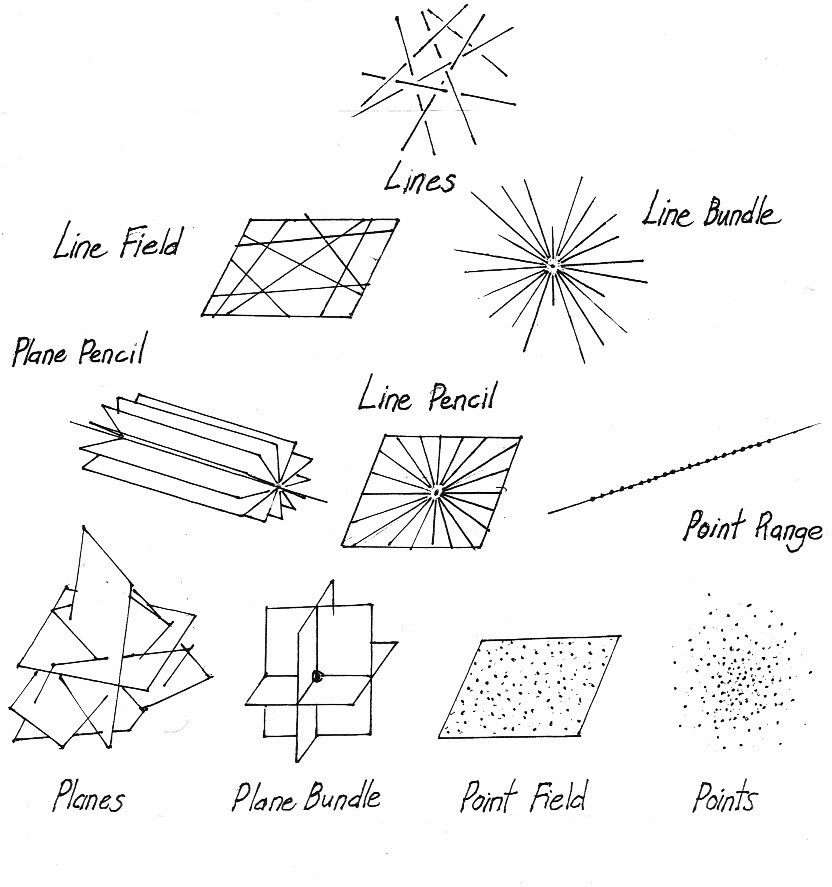
Start with the 3 basic spaces on the corners: points, lines, planes.
Drop an element from one space into another space and mark the incident elements.
This produces the six forms on the edges.
The line pencil arises from an incident point/plane pair dropped into line space.
3D Dictionary of duality
point
line of points (spear)
intersect
lie on
move along
segment
vertex
edge
plane bundle
line bundle
point range
plane
line of planes (axis)
join
pass through
rotate around
fan
face
edge
point field
line field
plane pencil
3D duality example
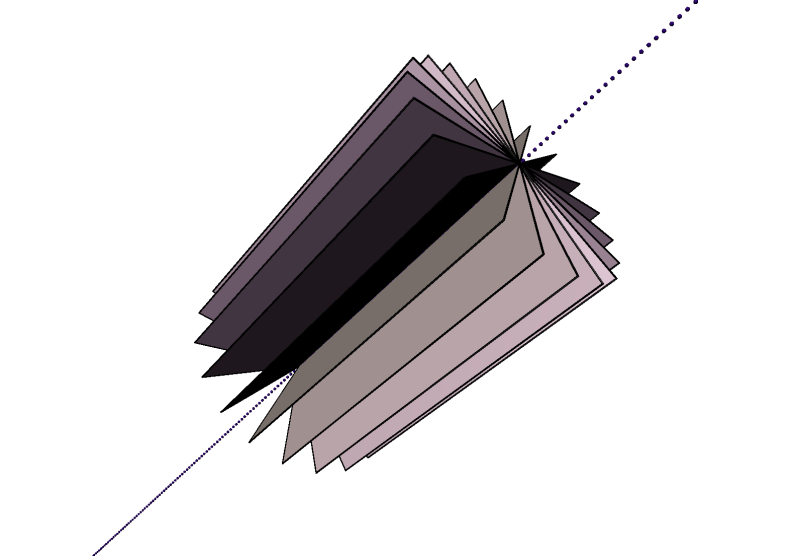
spear
axis
A velocity state in euclidean kinematics is an axis
A momentum/force state in euclidean dynamics is a spear.
Riddle: When is a line not a line?
Answer: When its a spear or an axis.
Cube and octahedron



The three joining lines of opposite vertices of the octahedron pass through the center point of the octahedron.
The three ______ ______ of opposite ______ of the cube _____ the center ______ of the cube.
Exercise
Fill in the blanks on the right.
Forward link: Counting subspace dimensions
In PGA, 1-vectors are
0-dimensional
indivisible
simple
whether they are point or plane.
The wedge operator \(\wedge\) determines how the world constructed.
| grade | standard GA | dual GA |
|---|---|---|
| 1 | point | plane |
| 2 | point range | plane pencil |
| 3 | point field | plane bundle |
The cross ratio: a projective invariant
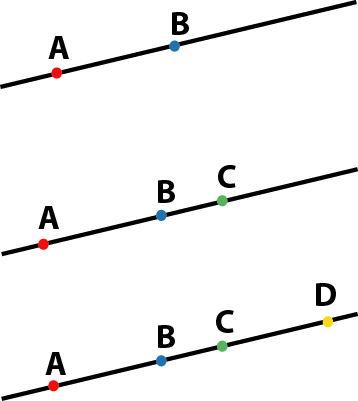
Metric geometry:
the distance \(AB\) is invariant.
Metric+uniform scaling:
the ratio \(\frac{AC}{AB}\) is invariant.
Projective geometry:
the double ratio \(\frac{AC}{AB}:\frac{DC}{DB}\) is invariant, also called cross ratio.
Harmonic points: cross ratio = -1
For further study
Being a gentle introduction to non-euclidean geometry and how spherical, hyperbolic, and euclidean geometries are all
PGA: Equal
*
*
equal
citizens in PGA.
Noneuclidean (metric) geometry
1820: Proving the parallel postulate.
Given a line and a point not on the line there exists exactly one line through the point parallel to the line.
Noneuclidean (metric) geometry
Euclid's fifth postulate can't be proved.
There are three possibilities.
| Name | Elliptic | Euclidean | Hyperbolic |
|---|---|---|---|
| # parallels | 0 | 1 | 2 |
| sum of angles | >180 | =180 | <180 |
| curvature | +1 | 0 | -1 |



Noneuclidean (metric) geometry



236
euclidean
235
elliptic
237
hyperbolic
The three triangle groups
3D: Three regular pentagon dodecahedra
euclidean
\(\alpha = 116.57^\circ\)
elliptic
\(\alpha = \frac{2\pi}{3}=120^\circ\)
hyperbolic
\(\alpha = \frac{\pi}{2}=90^\circ\)


Why learn about noneuclidean geometry?
- It's cool!
- Elliptic geometry \(\cong \frac12\) spherical geometry.
- Google: "hyperbolic geometric graph".
- "Almost all" 3-dimensional topological manifolds are hyperbolic. Poincare conjecture, Thurston's geometrization program, "Not Knot".
- Euclidean geometry is a limiting case of noneuclidean geometries.
"Not Knot" (Geometry Center, 1992)
Cayley-Klein geometry:
Metric geometry inside
projective geometry


"Projective geometry is all geometry."
Arthur Cayley (1821-1895)
Cayley-Klein geometry:
Metric geometry inside projective geometry


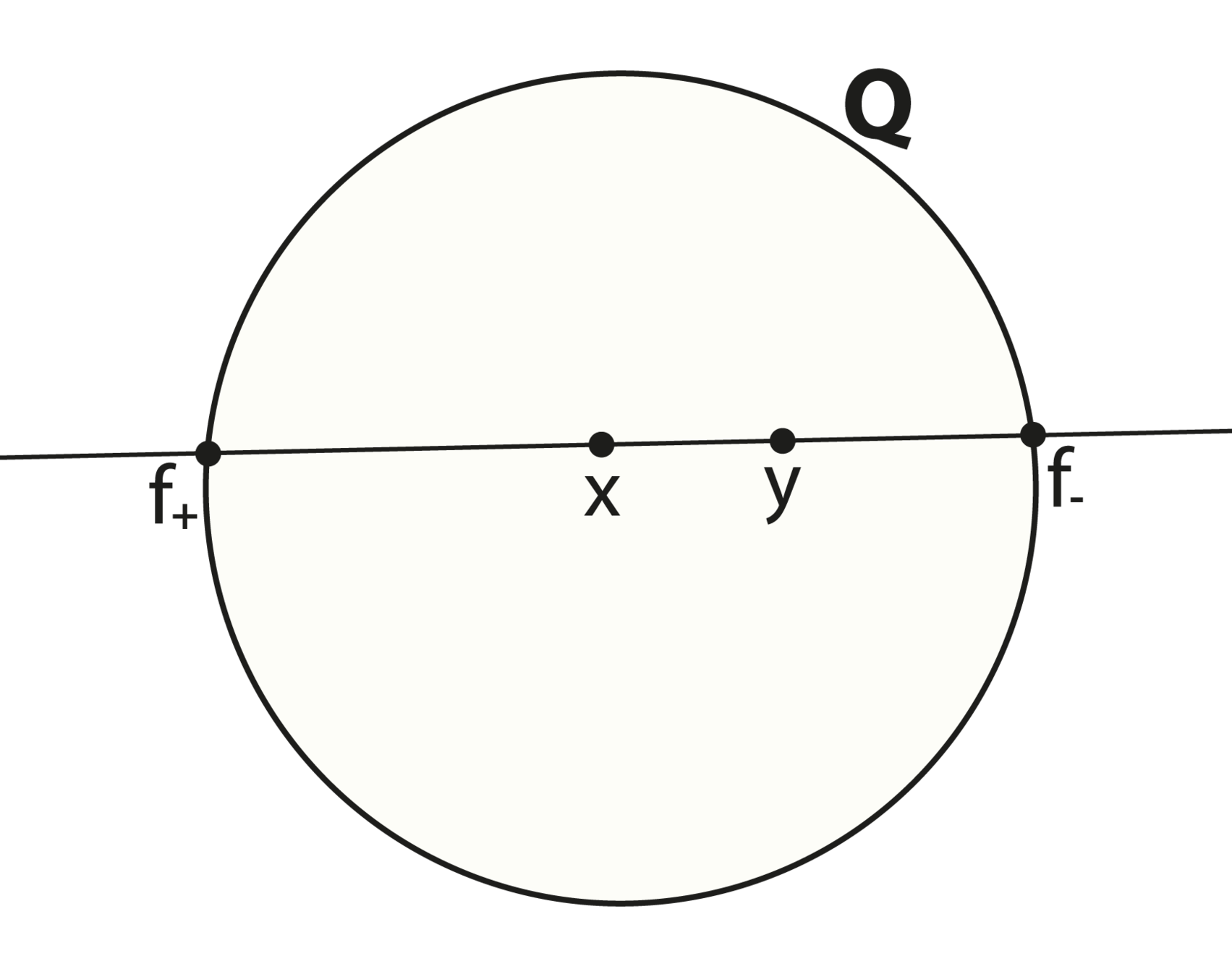
| Name | elliptic | euclidean | hyperbolic |
|---|---|---|---|
| signature | (3,0,0) | (2,0,1) | (2,1,0) |
| null points | |||
| null lines |
\(x^2+y^2+z^2\)=0
\(x^2+y^2-z^2\)=0
Cayley-Klein geometries for n = 2



\(a^2+b^2+c^2\)=0
\(x^2+y^2-z^2\)=0
\(a^2+b^2-c^2\)=0
\(a^2+b^2\)=0
\(z^2\)=0
PGA for Cayley-Klein spaces
\(P(\mathbb{R}^*_{n,1,0})\) or \(P(\mathbb{R}_{n,1,0})\): hyperbolic n-space
\(P(\mathbb{R}^*_{n+1,0,0})\) or \(P(\mathbb{R}_{n+1,0,0})\): elliptic n-space
We use the noneuclidean dual models since we want to generate the motion group using reflections in planes, not points.
The noneuclidean dual and standard algebras are equivalent since the metric is non-degenerate, i. e., \(\bf{X} \Rightarrow \bf{X}\bf{I}\) is an isomorphism.
\(P(\mathbb{R}^*_{n,0,1})\): euclidean n-space
\(P(\mathbb{R}_{n,0,1})\): dual euclidean n-space
PGA: multiplication by \(\bf{I}\)
Multiplication with \(\mathbf{I}\): For any k-vector \(\mathbf{x}\), \(\mathbf{x}^\perp := \mathbf{x}\mathbf{I}\) is the orthogonal complement of \(\mathbf{x}\).
This map is called the polarity on the metric quadric.
Example: \(\mathbf{e}_0 \mathbf{I} = \kappa\mathbf{e}_1\mathbf{e}_2\). The only thing left in \(\mathbf{I}\) is what isn't in \(\mathbf{X}\).
In noneuclidean PGA, multiplication by \(\bf{I}\) is a perfect partnership. Every element has a unique complement.
Appllied to the whole algebra, you obtain another geometry with the same signature.
But in euclidean and dual euclidean, NOT. Multiplying by \(I\) in the euclidean PGA collapses onto the ideal plane \(\bf{e}_0\).
Metric-neutral point and line calculations
\(\ell\) = line (vector)
\(P\) = point (bivector)
\(\ell P\) = line through \(P, \perp\) to \(\ell\)
\(\ell P\ell\) = reflection of \(P\) in \(\ell\)
\(P\ell P\) = reflection of \(\ell\) in \(P\)
\((\ell \cdot P)\ell\) = projection of \(P\) on \(\ell\)
\((P \cdot \ell)P\) = projection of \(\ell\) on \(P\)
Metric-neutral point and line calculations
Metric-neutral 2D PGA example
//Main idea: "rotation" center has to lie on
//perpendicular bisector of AA' AND
// on angle bisector of mm'
// Find intersection of m and m2 and
// line through a and a2
M=()=>(m^m2), a=()=>join(A,A2),
// Find the midpoint between A and A2 and the
// orthogonal line through it (| is inn. prod.)
Am=()=>(A+A2), r=()=>(a|Am),
// c is angle bisector of m and m2. Cut that
// with r to find the center point of isometry
c=()=>(m-m2), C=()=>(r^c),
// Construct the transformation as a "rotation"
// fixing C. (metric- and ideal-neutral)
s=()=>join(A,C), g=()=>(r*s),
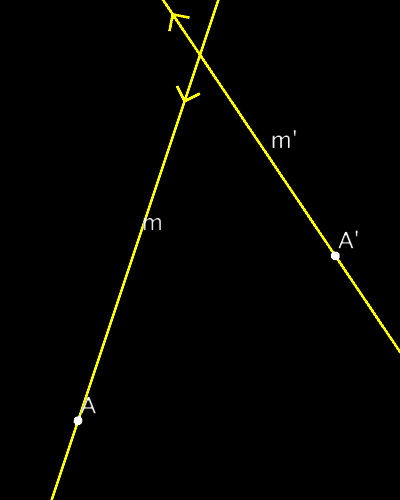
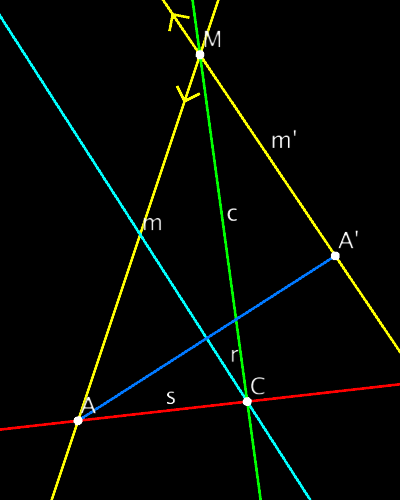
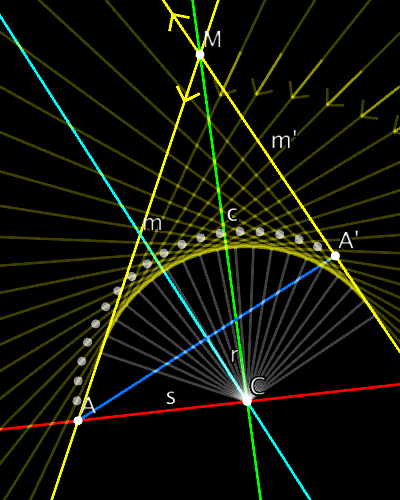
Metric neutral 2D PGA example
For further study
Charles Gunn, "Metric-neutral Visualization"
Charles Gunn, "Discrete groups and the visualization of 3-dimensional manifolds", SIGGRAPH 1993
Metric-neutral
rigid body mechanics
with PGA
Poinsot motion of the Euler top
Poinsot motion of the Euler top

The Euler top via PGA
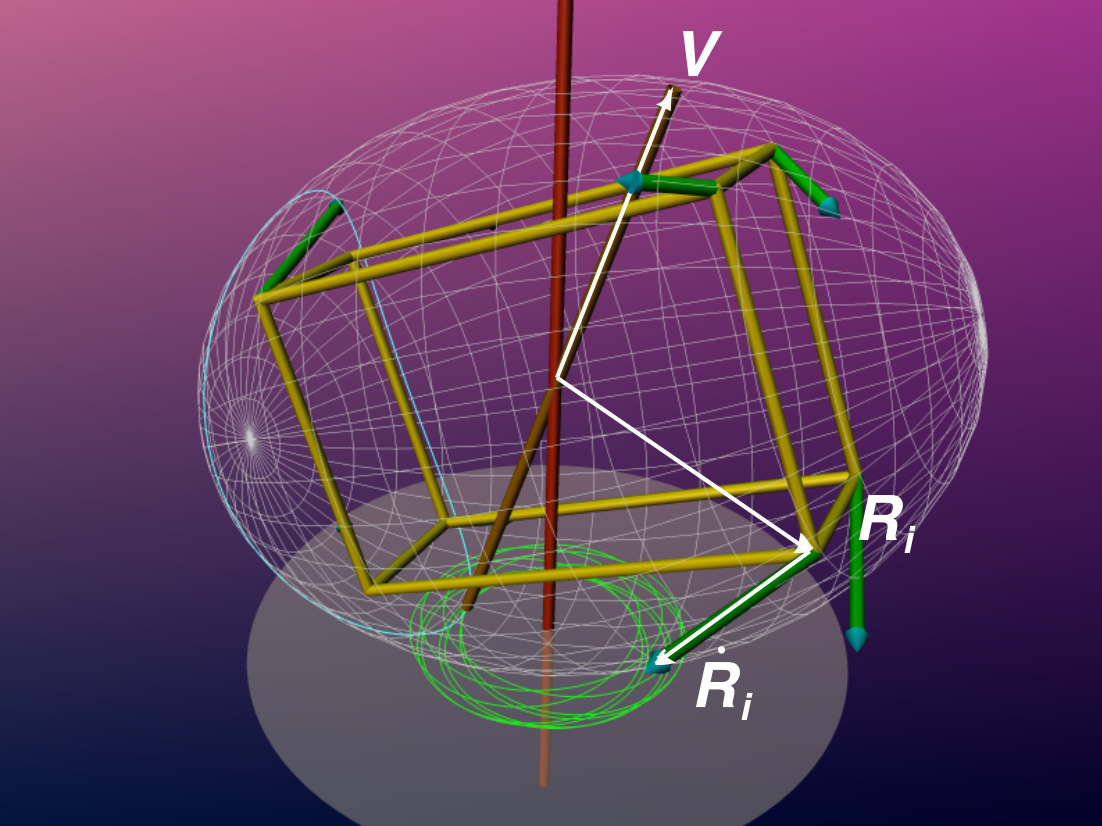
The global velocity state \(V\) is a line thru origin.
The velocity vector at R:
\[\dot{\bf{R}_i}=(\bf{R}_i\times \bf{V}) \] \[=(\bf{R}_i\vee \bf{V})\bf{I} \]
The momentum line:
\[\bf{M}_i := \dfrac{m_i}{2}(\dot{\bf{R}}_i \vee\bf{R}_i)\]
Kinetic energy of particle:
\[E_i = \bf{M}\vee\bf{V}\]
using inertia tensor:
\[E_i = A_i(\bf{V},\bf{V}) \]
\[\bf{M}_i = A_i(\bf{V},\circ) \]
*Note: \(\bf{X}\times\bf{Y} := \frac12 (\bf{X}\bf{Y} - \bf{Y}\bf{X})\)
The Euler top via PGA

Global momentum & energy
\[E := \sum_i E_i\]
\[ \bf{M} := \sum_i \bf{M}_i\]
\[ A := \sum_i A_i\]
\[ m := \sum_i m_i\]
Then by linearity:
\[ \bf{M} = A(\bf{V}, \circ)\]
\[E= \bf{M} \vee \bf{V}\]
Rigid body motion using 3D line geometry
The free top via PGA
All of the formulas derived for the Euler top remain true for the free top!
The only difference is that the velocity state \(\bf{V}\) can be any bivector (any arbitrary screw motion in space).
Also valid in any metric: behavior begins to be very different in the different metrics.
We look now at how the equations of motion look in PGA ...
Quaternion ODE's for Euler Top
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
Quaternion equations for the Euler top in \(\mathbb{R}^3\):
$$\dot{\mathbf{g}} = \mathbf{g} \mathbf{V}$$ $$ \dot{\mathbf{M}} = \frac12(\mathbf{V}\mathbf{M} - \mathbf{M} \mathbf{V}) $$
where \(\mathbf{g} \in \mathbb{U}\) and \(\mathbf{M}, \mathbf{V} \in \mathbb{IH}\) are the momentum, resp., velocity vectors in the body frame.
(\(\mathbf{M}={A}\mathbf{V}\) for inertia tensor \(A\)).
Metric-neutral Euler equations
for the free top in PGA
Given a rigid body with inertia tensor \(A\) under the influence of a global velocity state \(\bf{V}\).
Then the equations for the motion \(\bf{g}\) are given by the following ODE's:
\[\dot{\bf{g}} = \bf{g}\bf{V}_c\]
\[\dot{\bf{M}_c}=2(\bf{\bf{M}_c} \times \bf{V}_c) \]
where \(\bf {X_c}\) indicates use of body frame, \( \bf{\bf{M}_c} := A(\bf{\bf{V}_c})\) is the momentum state, and \(X \times Y := \frac12 (XY - YX)\) is the commutator product.
Noneuclidean rigid body motion
Advantages of PGA approach to kinematics and rigid body mechanics
It's metric-neutral.
In the euclidean case, it unifies many special cases:
It unifies linear and angular parts of momentum and velocity.
Force couples are forces carried by ideal lines.
Translations are "rotations" around ideal lines.
It also unifies many cases in the noneuclidean case too:-).
It has great numerical properties: 12D solution \(\subset\) 14D phase space
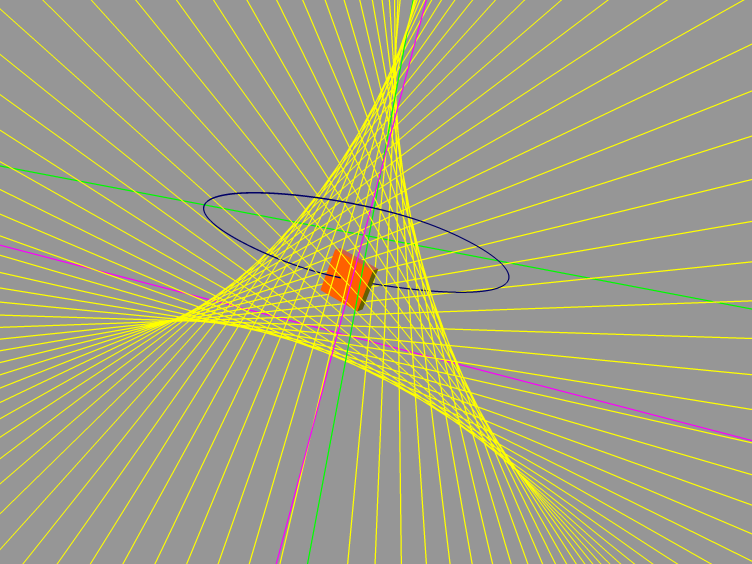


3D
Poinsot motion (?)
For further study
Charles Gunn, "Geometry, Kinematics, and Rigid Body Mechanics in Cayley-Klein Geometries", Ph. D. Thesis, 2011. On researchgate/charlesgunn
Looking to the future
PGA: Sequel
WARNING:
The rest of this presentation will be easier to digest if you are prepared to entertain the thought:
Brains don't think, people think.
2020: An anniversary for projective geometry
- Knowledge and understanding evolve, nothing is static.
- Projective geometry is relatively new field with room to grow.
- In 1420 it was born unconsciously with the appearance of perspective
- In 1620 it is was born consciously with Desargues' work integrating perspective into geometry (sense of sight).
- In 1820 it was re-established with a deeper understanding of duality.
- And now, in 2020?
- Euclidean PGA: planes and points as equal citizens in geometry.
- Is there perhaps more in PGA?
The ideal norm \(\|\bf{x}\|_\infty \)
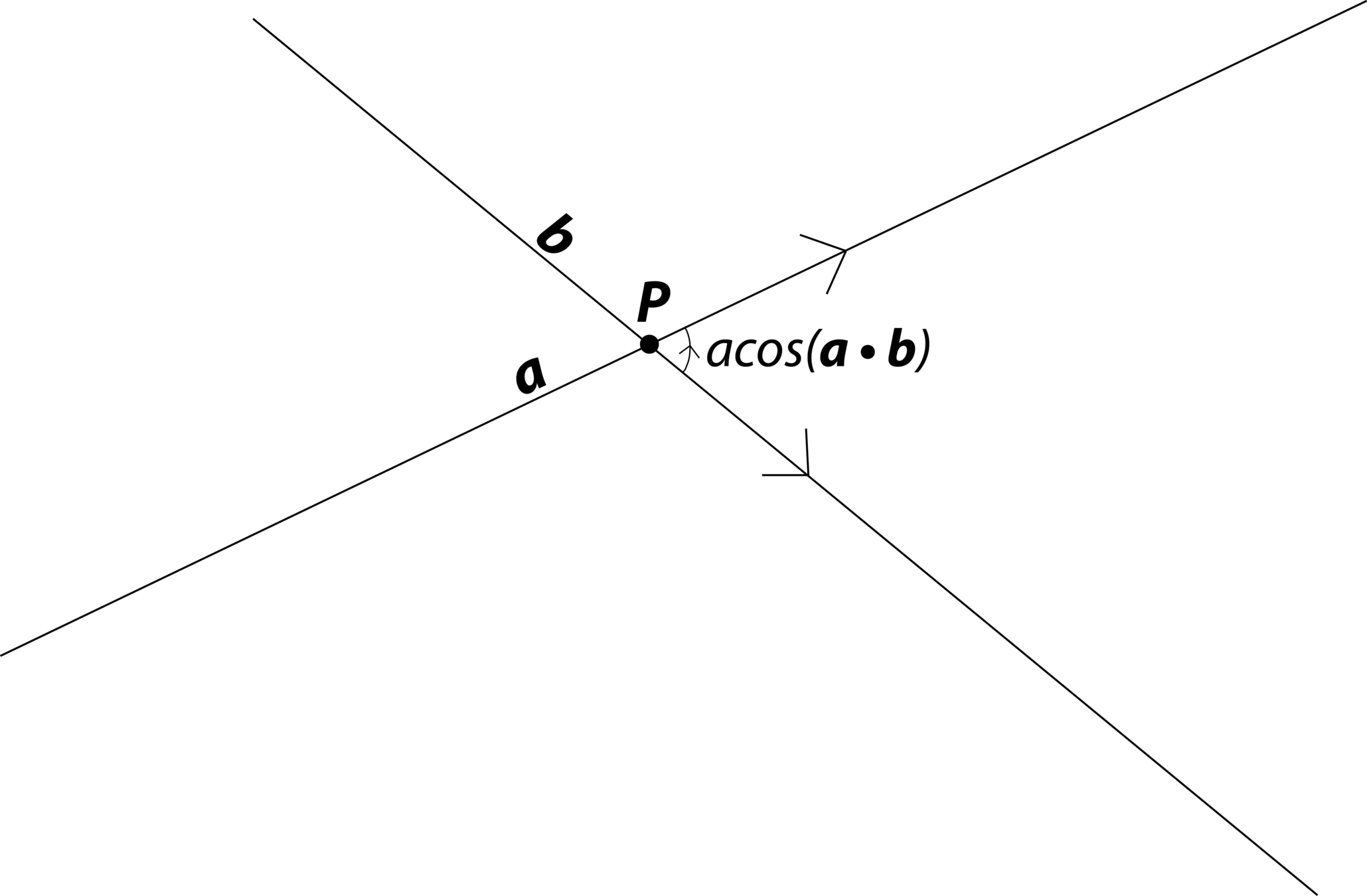
If (\(\|\bf{P}\|==1\)) then \(\bf{a}\wedge\bf{b} = \sin{\alpha}\bf{P}\)
and \(\bf e^{\alpha P}\bf{X}e^{-\alpha P}\) is a rotation of \(2\alpha\) around \(\bf{P}\).
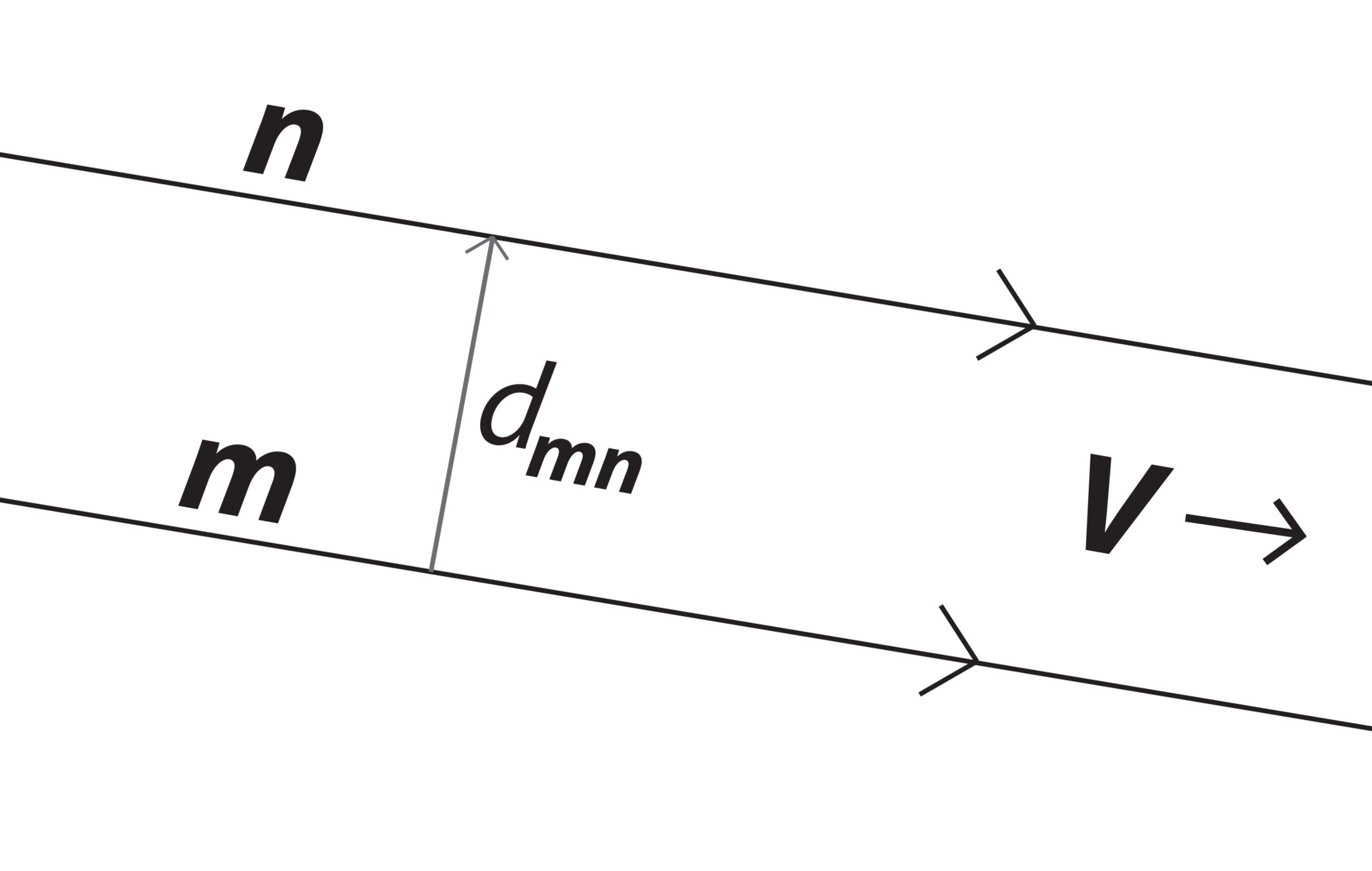
If (\(\|\bf{V}\|_\infty==1\)) then \(\bf{m}\wedge\bf{n} = d_{mn}\bf{V}\)
and \(\bf e^{d V}\bf{X}e^{-d V}\) is a translation of \(2d\) perpendicular to \(\bf{P}\).
\(=\alpha\)
POLYMORPHICITY
The ideal norm \(\|\bf{x}\|_\infty \)
- If (\(\|\bf{P}\|==1\)) and \(\bf{V}\) is ideal, then \( \|\bf{P} \vee\bf{V}\| =\|\bf{V}\|_\infty \)
- For a normalized line \(\bf{a}\) and a normalized ideal point \(\bf{V}\), \( \|\bf{a} \wedge\bf{V}\| =\sin{\alpha} \) where \(\alpha\) is the angle between \(\bf{V}\) and the direction of \(\bf{a}\).
- ...
- If (\(\|\bf{\ell}\|==1\)) and \(\bf{\ell}_\infty\) is a normalized ideal line meeting \(\ell\), then \( \bf{\ell} + d\bf{\ell}_\infty \) translates \(\bf{\ell}\) in the direction of \(\bf{\ell}_\infty\) the distance d.
- If (\(\|\bf{P}\|==1\)) and \(\bf{V}\) is a normalized ideal point, then \( \bf{P} + d\bf{V} \) translates \(\bf{P}\) in the direction of \(\bf{V}\) the distance d.
- If (\(\|\bf{a}\|==1\)) is a plane and \(\bf{\omega}\) is the normalized ideal plane, then \( \bf{a} + d\bf \omega \) translates \(\bf{a}\) in the direction of \(\bf{\omega}\) the distance d.
The ideal norm \(\|\bf{x}\|_\infty \) rules!
We can re-define the Poincare duality map to be a map between euclidean and dual euclidean space \[J: P(\mathbb{R}^*_{3,0,1})\Rightarrow P(\mathbb{R}_{3,0,1})\]
Then
\[\|\bf{X}\|_\infty = \|J(\bf{X})\|\]
Even more is true! The standard norm can also be defined in terms of the ideal norm:
\[\|\bf{X}\| = \|\bf{X}\wedge\omega)\|_\infty\]
where \(\bf X\) is a euclidean k-vector and \(\omega\) is the ideal plane.
The ideal norm can be seen as the source of the euclidean metric (since the norm determines the inner product).
And since it comes from dual euclidean space (aka counterspace) it makes sense to take a closer look at \(P(\mathbb{R}_{3,0,1})\).
\(P(\mathbb{R}_{n,0,1})\)
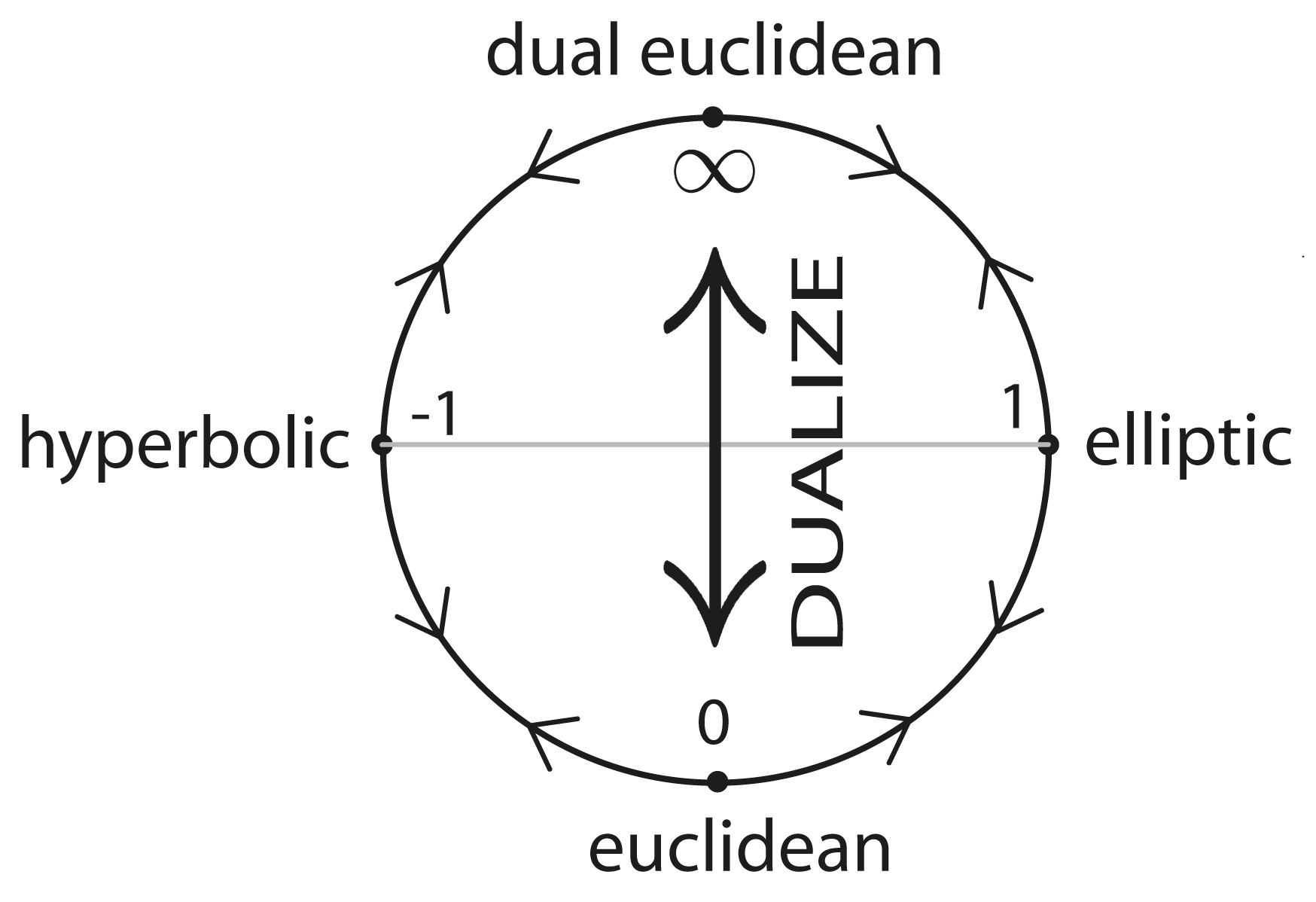
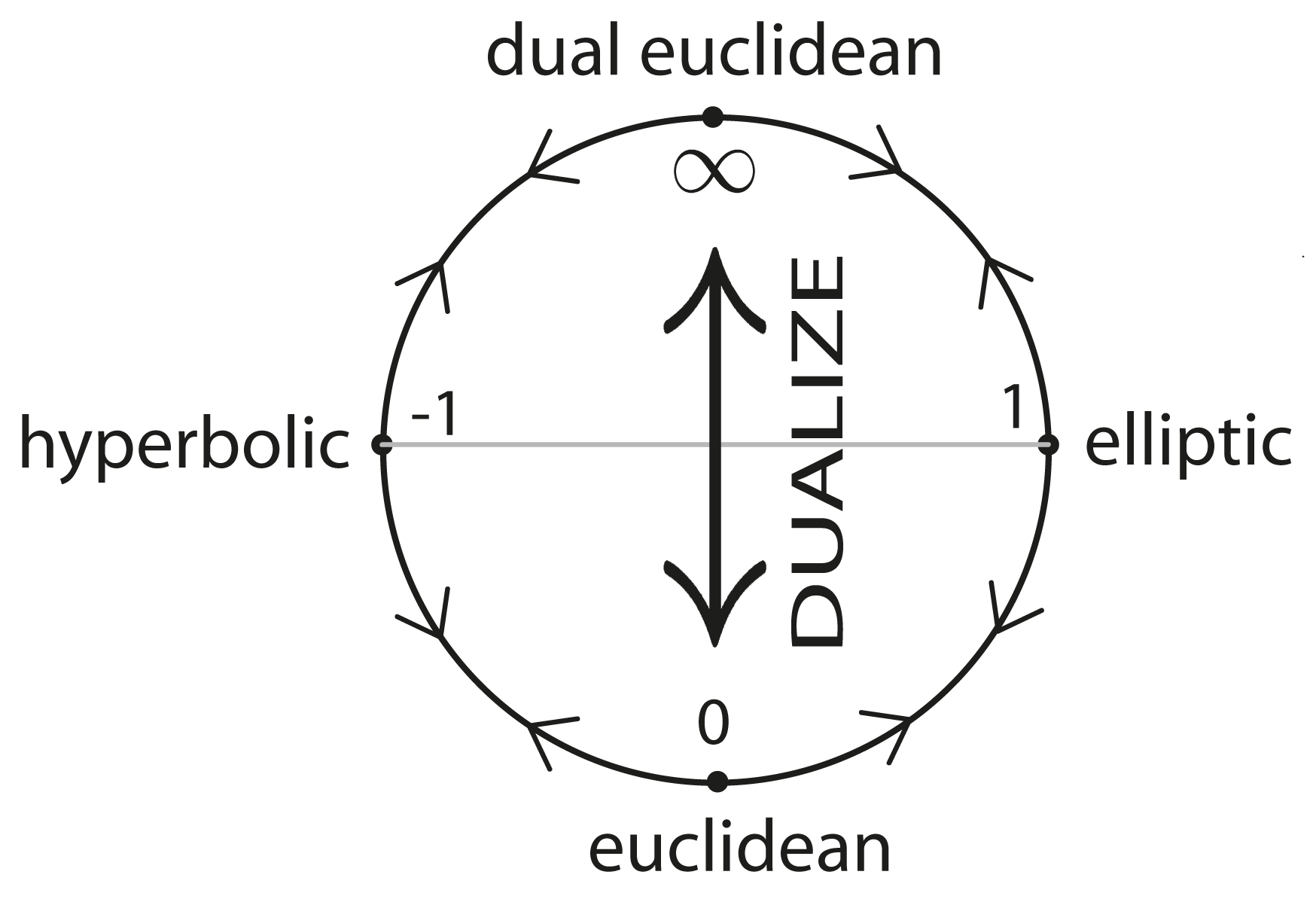
The circle of geometries
\(P(\mathbb{R}^*_{n,0,1})\)
\(P(\mathbb{R}^*_{n,1,0})\)
\(P(\mathbb{R}^*_{n+1,0,0})\)
DRAFT
Counterspace 101
Counterspace
Recap:
Counterspace is the dualization of euclidean space within projective geometry. It swaps:
- Inside and outside
- center and periphery
- large and small
- contraction and expansion
- ...
"Objects" in counterspace are hollow, made of planes, surrounding the ideal point (hulls, not kernels).
Let's do a little calculation in counterspace ...
Vectors in Counterspace
- Exercise: Given a counterspace vector based at \(e_0\), compute its length.
What is a CS vector? It is obtained by rotating a line from a beginning position (in this case \(e_0\)) to an end position say \(a = de_0 + e_2\).
a: y = d
O
d
Normalize in CS: \(o = e_0, a = e_0+ \frac1d e_2\)
\(\|oa\| = \|o-a\|_\infty = \frac1d\)
This means: the CS distance \(oa = \frac{1}{Oa}\) where \(Oa\) is the euclidean distance from \(O=E_0\) to \(a\).
A problem in statics
The three wires a', b', c' meet in point O and lie in a plane.
A weight is attached to wire a'. You want to know the forces on b' and c'.
In graphics statics this is calculated by drawing lines a', b', c' \(\perp\) to a, b, c, to form triangle ABC so that AB = force due to weight.
Then the forces are the vectors AB:BC:CA (rotated 90 degrees).
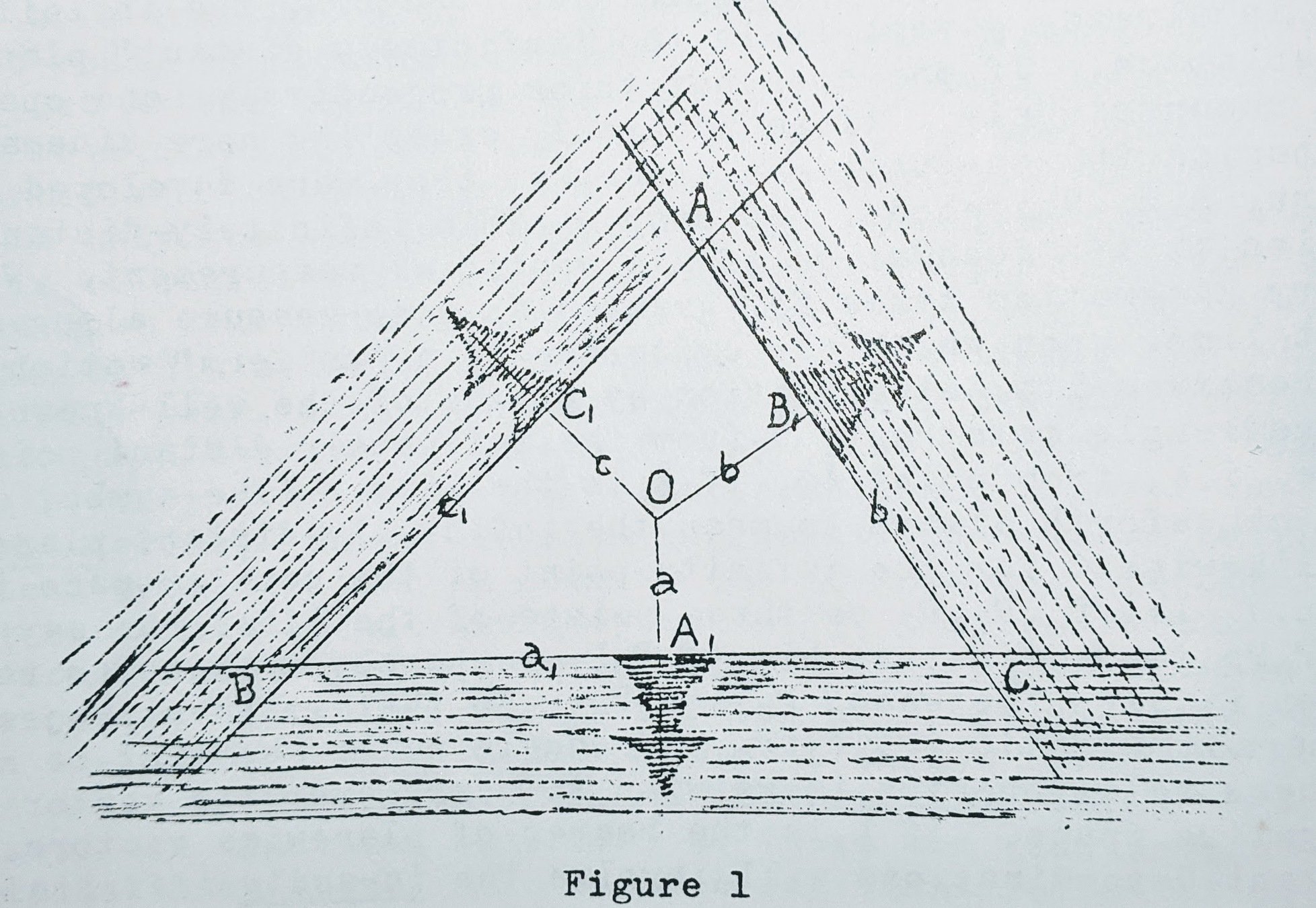
A problem in statics
Consider the counterspace vectors oa, ob, oc (where \(o = e_0\) is the origin of CS, and O is the ideal pt of the CS.
We position the triangle so that O is its centroid. Let D be the area of triangle. Then \(OC_1(AB) = OA_1(BC) = OB_1(CA) = \frac23 D\).
So \(BC:CA:AB = \frac{1}{OA_1}:\frac{1}{OB_1}:\frac{1}{OC_1}\).
By the exercise \(oa = \frac1{OA_1}\), etc. So \(AB:BC:CA = oa:ob:oc\).

A problem in statics
When the meeting point of a, b, c is the centroid of the triangle and the ideal point of the CS, then the forces in equilibrium can be read out from the diagram in two ways:

- The vectors BC, CA, AB, rotated 90 degrees, represent the forces carried by the lines a, b, c. ("Graphic statics")
- The CS vectors \(oa_1,ob_1,oc_1\) also represent the forces on a, b, c since \(oa_1:ob_1:oc_1 = BC:CA:AB\).
A problem in statics
This example shows how traditional methods for working with forces are compatible with interpreting them as vectors in counterspace.
This is good since representing a force as a vector mixes up kinematics (extension) with dynamicjs (non-extended).

See George Adams, "Universal Forces in Mechanics" for more information.
Is this just a coincidence?
Or does counterspace have a place in the bigger picture?
What is the bigger picture?
A short history of cognition and science
- Theory of cognition: Sense perception + human thinking = reality
- Not all senses equal: primary and secondary sense perceptions.
- Primary ones are extended hence measurable (length, number, etc).
- For our purposes, "primary" \(\cong\) sense of touch.
- For example, color is thought of as a form of radiation moving through space that interacts with human nervous system (also in space) to produce the "subjective" sensation of "red".
- Results in "subject-object split"
- object: the extended world containing our extended body.
- subject: inner world of consciousness or "soul"
- When: Galileo, Descartes, Newton, Locke... \(~1600-)\).
- Leading to modern science and technology: wonderful success!
A short history of space and science
- Rene Descartes (1596-1650) added algebra to euclidean geometry to produce cartesian geometry, basis for Newtonian science.
- Rene Desargues ( 1591-1661) introduced ideal points to euclidean space to create projective geometry.
- Newtonian science grew and conquered ever new domains. PG disappeared.
- Jean Poncelet (1788-1867) rediscovered PG again, this time for good. It quickly permeated the world of higher mathematics.
- The noneuclidean metric geometries were discovered! (1830)
- Cayley and Klein showed that these geometries live in PG (1860).
-
Bernard Riemann's (1826-1866) "empirical space hypothesis"
- Space itself is an object of empirical research -- finding the right space to match the observed phenomena. (1854)
- Riemannian manifold is an arbitrarily "curved" space form that looks locally like euclidean space.
- Has had great influence on development of modern physics.
A short history of space and science
-
But: counterspace was left out since it is not a Riemannian manifold.
- It is of course a dual Riemannian manifold because it is locally (and globally) a dual euclidean space:-)
- Given the efficacy of euclidean PGA as proven in 2020, perhaps Riemann's restriction to point-based manifolds is not justified.
- If so, it would make sense to take a closer look at this "perfect partner" of euclidean space as a candidate space for doing empirical science.
Raising a-where-ness
- Geometry is closely linked with the "where" question.
- Euclidean space reveals the "where" of our tactile space.
- PG answers the question "Where do parallel lines meet?"
- It does so by extending euclidean geometry to include visual space ( forming an organic whole.
- At around the same time as PG appeared, the human being turned his attention to focus exclusively on the "outer" world.
- This meant seeing himself has an element of that outer world, determined by its laws alone.
- And thereby "forgot" the inner world of his own consciousness.
- With limited success (this would be a good discussion given time).
- Qutestion arises: Can we extend our geometry to give equal citizenship to this most intimate but strange aspect of existence?
- N. B.: without in any way contradicting the truth and validity of the outer world and its laws?
Example of how inner and outer meet
The painting in the outer world is a point field.
When it enters my consciousness it becomes a bundle.
My awareness is the center of this bundle.
It is in the bundle that meaning and story arises.
In this way I establish a connection to the "bundle" of the painter.



Inner - conscious
outer - material
This has features of space - counterspace duality
Three fold space-sense diagram
Projective space
Space
Counterspace
Sight
Thinking
Touch
DUALITY
Inner
Outer
Human being in space and counterspace
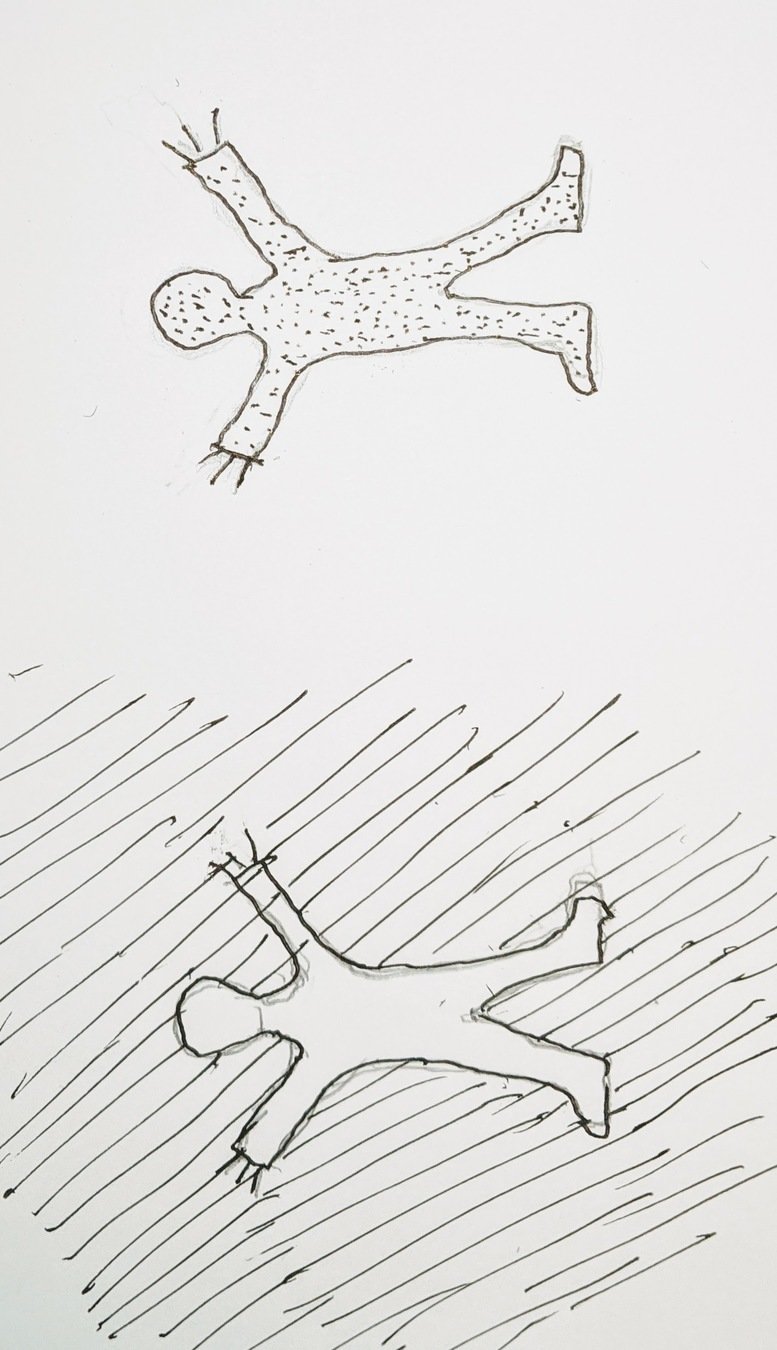

Where am I when I say "Here I am"?
Me and you in space and counterspace

Parting thoughts
Text
I'm presenting questions here, not answers.
The underlying thoughts have kept me busy for 40 years and I feel that I am just beginning.
The success of PGA after a long dry spell reminds me that all new ideas have their time.
The story we are telling individually and collectively
can't be rushed and it can't be owned.
If there is any chance that we can build a bridge between the outer world of science and the individual world we each bear within -- then it seems to be a goal worth pursuing.
If it's half as fun as PGA, then I'm in!


1980 I met the work of George Adams, pioneer of duality.
Questions and comments: projgeom at gmail.com
Thanks for your attention!
For further study
George Adams, "Universal Forces in Mechanics"
George Adams and Olive Whicher, "The Plant Between Earth and Sun", 1952
Ernst Lehrs, "Man or Matter", 2014
That's all folks
What is Cayley-Klein geometry?


| Signature of Q | Space | Symbol | |
|---|---|---|---|
| +1 | elliptic | ||
| -1 | hyperbolic | ||
| 0 | euclidean |
\((n+1,0,0)\)
$$\bf{E}^n$$
$$\bf{H}^n$$
$$\bf{Ell}^n,\bf{S}^n$$
\((n,1,0)\)
\("(n,0,1)"\)
\(\kappa\)
| Name | elliptic | euclidean | hyperbolic |
|---|---|---|---|
| signature | (3,0,0) | "(2,0,1)" | (2,1,0) |
| null points | |||
| null lines* |
\(x^2+y^2+z^2\)=0
\(z^2\)=0
\(x^2+y^2-z^2\)=0
\(a^2+b^2+c^2\)=0
\(a^2+b^2-c^2\)=0
\(a^2+b^2\)=0
*The line \(ax+by+cz=0\) has line coordinates \((a,b,c)\).



Example Cayley-Klein geometries for n = 2
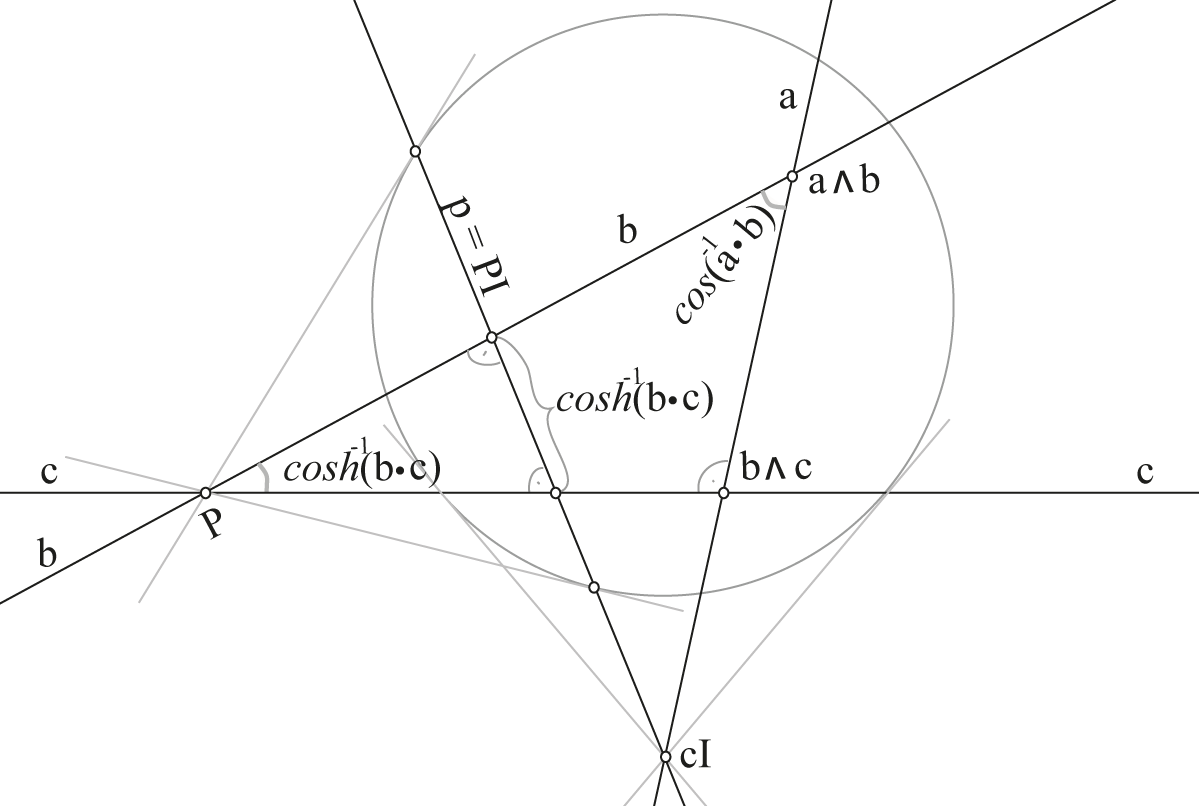
PGA: 2-way products
Product of two proper lines \(\mathbf{b},\mathbf{c}\): \(\kappa = -1\), \(\mathbf{P}\) is hyper-ideal.
$$\mathbf{b}\mathbf{c} = \cosh(d) + \sinh(d)\mathbf{P}$$
where \(d\) is the hyperbolic distance between the lines.
Question
What is the best way
to do Cayley-Klein geometry
on the computer?


1993
2019

Projective
points
Projective
matrices
Vector + linear algebra
Projective
points
Projective
matrices
Vector + linear algebra
But it's 2019 now. Can we do better?

Coordinate-free
Uniform rep'n for points, lines, and planes
Cayley-Klein programmer's wish list

Single, uniform rep'n for isometries
Parallel-safe meet and join operators
Compact expressions for classical geometric results
Physics-ready
Metric-neutral
Backwards compatible
Projective Geometric Algebra:
Prequel - Equal - Sequel
Charles Gunn
February 28, 2020 at GAME2020, Kortrijk
Slides available at: https://slides.com/charlesgunn3/pga-game2020.
The ideal norm via noneuclidean geometry
POLYMORPHICITY
A sketch
- The euclidean case is a limiting case of noneuclidean ones with signature \((1,1,\pm\epsilon)\).
- The plane \(\bf e_0\) is unchanged as \(\epsilon\) changes and has the metric \((3,0,0)\).
- Hence, it is indifferent to the limit and should retain the metric in euclidean space. This gives rise to the ideal norm \(\|...\|_\infty\).
- We call the associated inner product the ideal inner product.
- Then the inner product on euclidean planes is determined by the ideal inner product: \(\
(\(P(\mathbb{R}_{n,0,1})\))
What is dual euclidean space?
- It has an ideal point and all its lines and planes.
- The angle between two points is the angle between their joining lines to the ideal point.
CS and the subject-object split
Recall: Sense perception + human thinking = reality
Currently only the object side has a place in the scientific world. That is the extended world, the world of touch, Euclidean space (and its point-based modern variations).
Projective geometry adds the geometry of sight and thereby creates new places, where parallel lines meet.
It also thereby establishes duality, that makes it possible to dualize physical space to obtain counterspace.
Sense-perception stands over against thinking,
Euclidean space stands over against counterspace.
What if the inner world of consciousness were a counterspace?
Unfortunately the margin of this page is not large enough for the proof.

Partial solutions: Quaternions (1843)
A 4D algebra generated by units \(\{1,\mathbf{i},\mathbf{j},\mathbf{k}\}\) satisfying:
$$1^2=1,~~\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2=-1$$ $$\mathbf{i}\mathbf{j}=-\mathbf{j}\mathbf{i},\text{...}$$
Quaternions
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
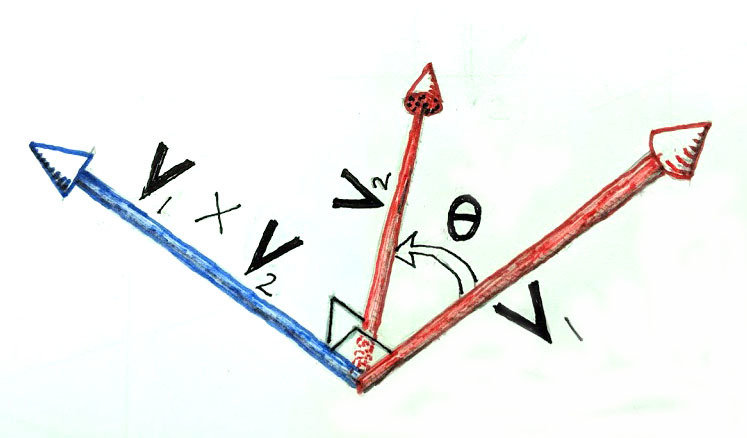
I. Geometric product:
$$\mathbf{v}_1\mathbf{v}_2 = -\mathbf{v}_1 \cdot \mathbf{v}_2 + \mathbf{v}_1 \times \mathbf{v}_2$$
cross product
inner product
Quaternions
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
II. Rotations via sandwiches:
1. For \(\mathbf{g} \in \mathbb{U}\), there exists \(\mathbf{x} \in \mathbb{IH}\) so that
$$\mathbf{g} = \cos(t)+\sin(t)\mathbf{x} = e^{t\mathbf{x}}$$
2. For any \(\mathbf{v} \in \mathbb{IH}~~ (\cong \mathbb{R}^3)\), the "sandwich" $$ \mathbf{g}\mathbf{v}\overline\mathbf{g}$$ rotates \(\mathbf{v}\) around the axis \(\mathbf{x}\) by an angle \(2t\).
3. Comparison to matrices.
Quaternions
Quaternions \(\mathbb{H}\)
Im. quaternions \(\mathbb{IH}\)
Unit quaternions \(\mathbb{U} \)
$$s+x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$$
$$ \mathbf{v} := x\mathbf{i}+y\mathbf{j}+z\mathbf{k} \Leftrightarrow (x,y,z) \in \mathbb{R}^3 $$
$$\{\mathbf{g}\in\mathbb{H} \mid \mathbf{g}\overline{\mathbf{g}}= 1\}$$
Advantages
I. Geometric product
II. Rotations as sandwiches
Disadvantages
I. Only applies to points/vectors
II. Special case \(\mathbb{R}^3\)
Quaternions
Partial solutions: Grassmann algebra

Hermann Grassmann (1809-1877)
Ausdehnungslehre (1844)
Grassmann algebra
The wedge (\(\wedge\)) product in \(\mathbb{R}P^2\) and \(\mathbb{R}P^{2\large*}\)
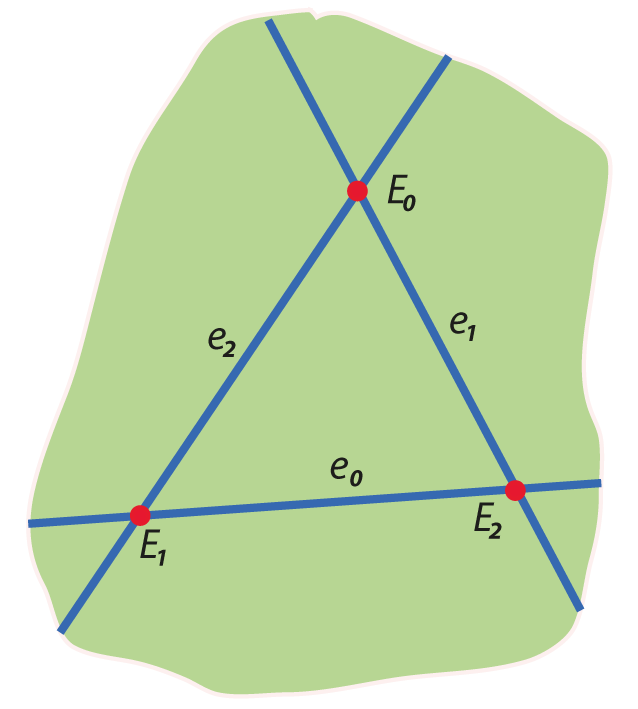
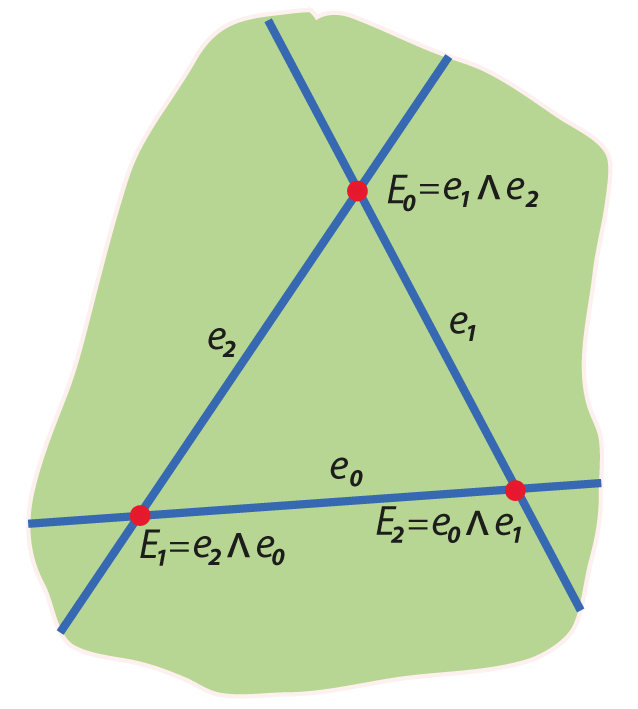
Standard projective
\(\mathbf{x}\wedge\mathbf{y}\) is join
yields \(\bigwedge\mathbb{R}P^2\)
Dual projective
\(\mathbf{x}\wedge\mathbf{y}\) is meet
yields \(\bigwedge\mathbb{R}P^{2\large*}\)
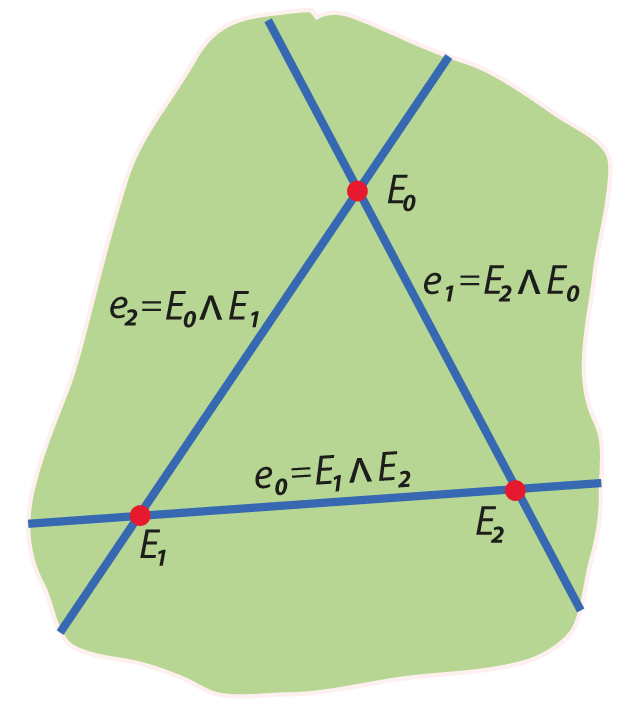
Grassmann algebra

| Grade | Sym | Generators | Dim. | Type |
|---|---|---|---|---|
| 0 | 1 | 1 | Scalar | |
| 1 | 3 | Line | ||
| 2 | 3 | Point | ||
| 3 | 1 | Pseudoscalar |
\(\bigwedge^3\)
\(\bigwedge^2\)
\(\bigwedge^1\)
\(\bigwedge^0\)
\(\{\mathbf{e}_0,\mathbf{e}_1,\mathbf{e}_2\}\)
\(\{\mathbf{E}_i = \mathbf{e}_j\wedge\mathbf{e}_k\}\)
\(\mathbf{I}=\mathbf{e}_0\wedge\mathbf{e}_1\wedge\mathbf{e}_2\)
We will be using \(\bigwedge\mathbb{R}P^{n\large{*}}\) for the rest of the talk.
The dual projective Grassmann algebra \(\bigwedge\mathbb{R}P^{2\large*}\)
Grassmann algebra
Properties of \(\wedge\)
1. Antisymmetric: For 1-vectors \(\mathbf{x}, \mathbf{y}\):$$\mathbf{x}\wedge\mathbf{y}=-\mathbf{y}\wedge\mathbf{x}$$$$\mathbf{x}\wedge\mathbf{x}=0$$
2. Subspace lattice: For linearly independent subspaces \(\mathbf{x}\in\bigwedge^k,\mathbf{y}\in\bigwedge^{m}\), \(\mathbf{x}\wedge\mathbf{y}\in\bigwedge^{k+m}\) is the subspace spanned by \(\mathbf{x}\) and \(\mathbf{y}\) otherwise it's zero.

Note: The regressive (join) product \(\large\vee\) is also available.
(Then it's called a Grassmann-Cayley algebra.)
The wedge (\(\wedge\)) product in \(\mathbb{R}P^2\)
Grassmann algebra
Note: spanning subspace means different things in standard and dual setting. In 3D:

Standard: a line is the subspace spanned by two points.
Dual: a line is the subspace spanned by two planes.
Point range
Spear
Plane pencil
Axis
Grassmann algebra
Advantages
1. Points, lines, and planes are equal citizens.
2. "Parallel-safe" meet and join operators since projective.
Disadvantages
1. Only incidence (projective), no metric.
Grassmann algebra
Clifford's geometric algebra

William Kingdon Clifford (1845-1879)
"Applications of Grassmann's extensive algebra" (1878):
His stated aim: to combine quaternions with Grassmann algebra.
Clifford's geometric algebra
Geometric product extends the wedge product and is defined for two 1-vectors as: $$\large{\mathbf{x}\mathbf{y} := \mathbf{x}\large{\cdot}\mathbf{y} + \mathbf{x}\wedge\mathbf{y}}$$
where \(\cdot\) is the inner product induced by \(\mathbf{Q}\).
0-vector
2-vector
This product can be extended to the whole Grassmann algebra to produce the geometric algebra \(\mathbf{P}(\mathbb{R}^*_{p,n,z})\).
measures sameness
measures difference
Since the two terms measure different aspects, the sum is (usually) non-zero.
Projective geometric algebra
We call an algebra constructed in this way a projective geometric algebra (PGA).
We are interested in \(\mathbf{P}(\mathbb{R}^*_{3,0,0}) \), \(\mathbf{P}(\mathbb{R}^*_{2,1,0}) \), \(\mathbf{P}(\mathbb{R}^*_{2,0,1}) \).
We sometimes write \(\mathbf{P}(\mathbb{R}^*_\kappa)\) and leave the metric open.
We can choose a fundamental triangle so that:
$$\mathbf{e}_0^2 = \kappa, \mathbf{e}_1^2=\mathbf{e}_2^2=1$$ $$(\kappa\in\{-1,0,1\})$$
$$\mathbf{E}_k:=\mathbf{e}_i\mathbf{e}_j = \mathbf{e}_i\wedge\mathbf{e}_j = -\mathbf{e}_j\mathbf{e}_i$$
$$\mathbf{I}:=\mathbf{e}_0\mathbf{e}_1\mathbf{e}_2$$
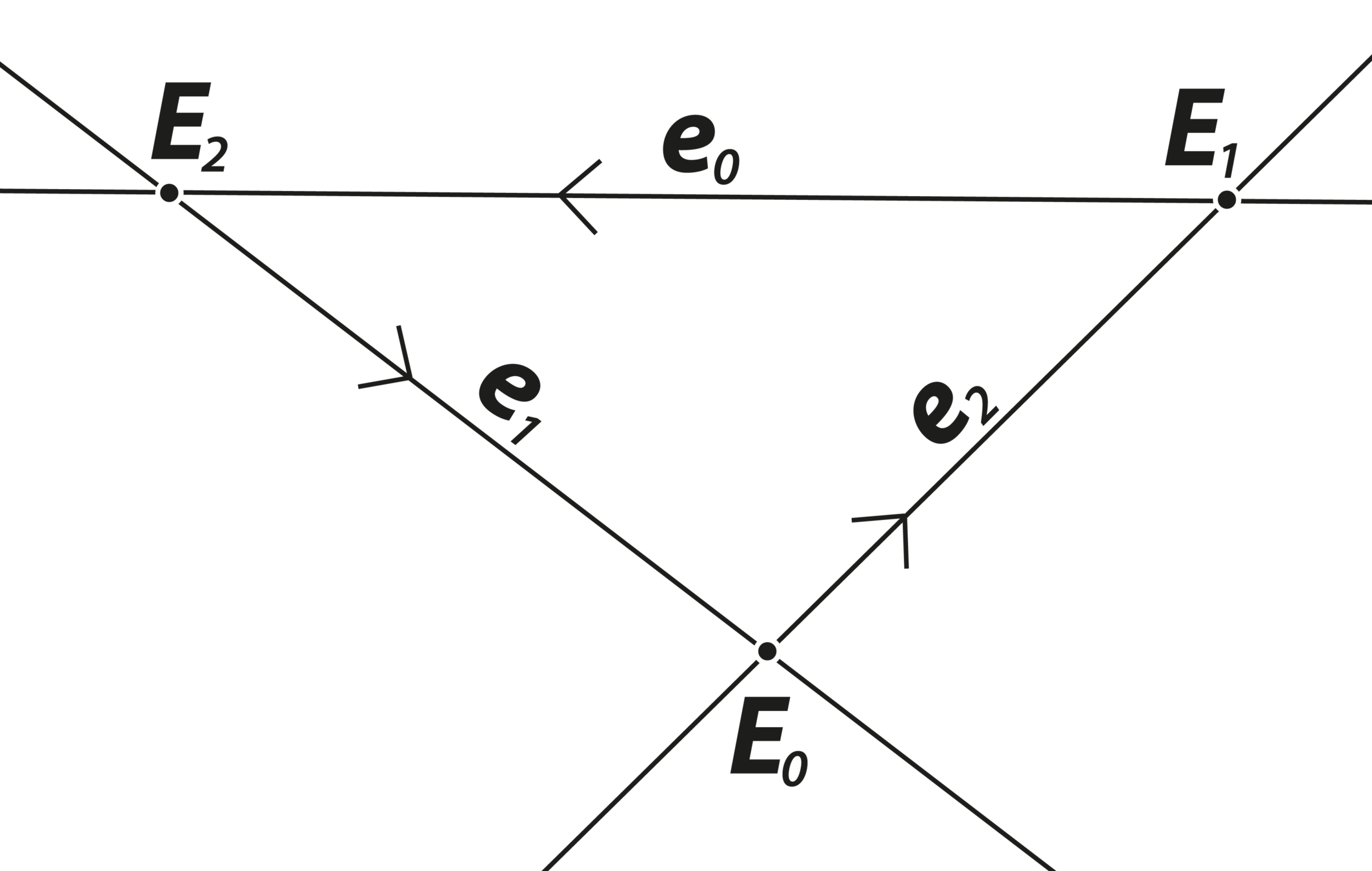
2D PGA
Example: Two lines, let \(e_0^2=\kappa\) $$\mathbf{a} = a_0 e_0+a_1 e_1 + a_2 e_2$$ $$ \mathbf{b} = b_0 e_0 + b_1e_1+b_2e_2$$ $$\mathbf{ab}=(a_0b_0e_0^2+a_1b_1e_1^2+a_2b_2e_2^2)$$ $$+(a_0b_1 - a_1b_0)e_0e_1 + (a_1b_2-a_2b_1)e_1e_2 + (a_0b_2-a_2b_0)e_0e_2$$ $$ = (a_0b_0\kappa+a_1b_1+a_2b_2)$$ $$+(a_1b_2-a_2b_1)E_0+(a_2b_0-a_0b_2)E_1+(a_0b_1-a_1b_0)E_2$$ $$= \mathbf{a}\cdot \mathbf{b} + \mathbf{a}\wedge \mathbf{b}$$
Looks like cross product but is the point incident to both lines.
2D PGA
Example: \(\kappa=1\) and \(c=\frac1{\sqrt{2}}\) and $$\mathbf{a} = e_0,~~~\mathbf{b} = ce_0+ ce_1$$
Then \(\mathbf{a}^2=\mathbf{b}^2=1\).
\(\mathbf{a}\) is the equator great circle \(z=0\) and \(\mathbf{b}\) is tilted up from it an angle of \(45^\circ\). $$\mathbf{ab}= c+E_2$$ Check: \(\cos^{-1}(c) = 45^\circ\) and \(\mathbf{E}_2\) is the common point.
2D Euclidean PGA
We can now explain why \(P(\mathbb{R}^*_{2,0,1})\) is the right choice for the euclidean plane.
The inner product of two lines is $$\mathbf{a\cdot b}= (a_0b_0\kappa+a_1b_1+a_2b_2)$$
For a euclidean line changing \(a_0\) or \(b_0\) doesn't change the direction of the line. It just moves it parallel to itself. This means \(e_0^2=0\).

PGA: 2-way products
Multiplication with \(\mathbf{I}\): For any k-vector \(\mathbf{x}\), \(\mathbf{x}^\perp := \mathbf{x}\mathbf{I}\) is the orthogonal complement of \(\mathbf{x}\).
Example: \(\mathbf{e}_0 \mathbf{I} = \kappa\mathbf{e}_1\mathbf{e}_2\). The only thing left in \(\mathbf{I}\) is what isn't in \(\mathbf{X}\).

PGA: 2-way products
Product of two proper lines \(\mathbf{a},\mathbf{b}\) that meet at a proper point \(\mathbf{P}\):
$$\mathbf{a}\mathbf{b} = \cos(t) + \sin{(t)}\mathbf{P}$$
where \(t\) is the angle between the lines (arbitrary \(\kappa\)).

PGA: 2-way products
Product of proper line \(\mathbf{c}\) and proper point \(\mathbf{Q}\):
$$\mathbf{c}\mathbf{Q} = \mathbf{c} \cdot \mathbf{Q} + (\cosh{d)}\mathbf{I}~(=\langle cQ\rangle_1+\langle cQ \rangle_3)$$
The first term is the line through \(\mathbf{Q}\) perpendicular to \(\mathbf{c}\), sometimes written \(\mathbf{c}^\perp_\mathbf{Q}\). \(d\) is the distance from point to line.
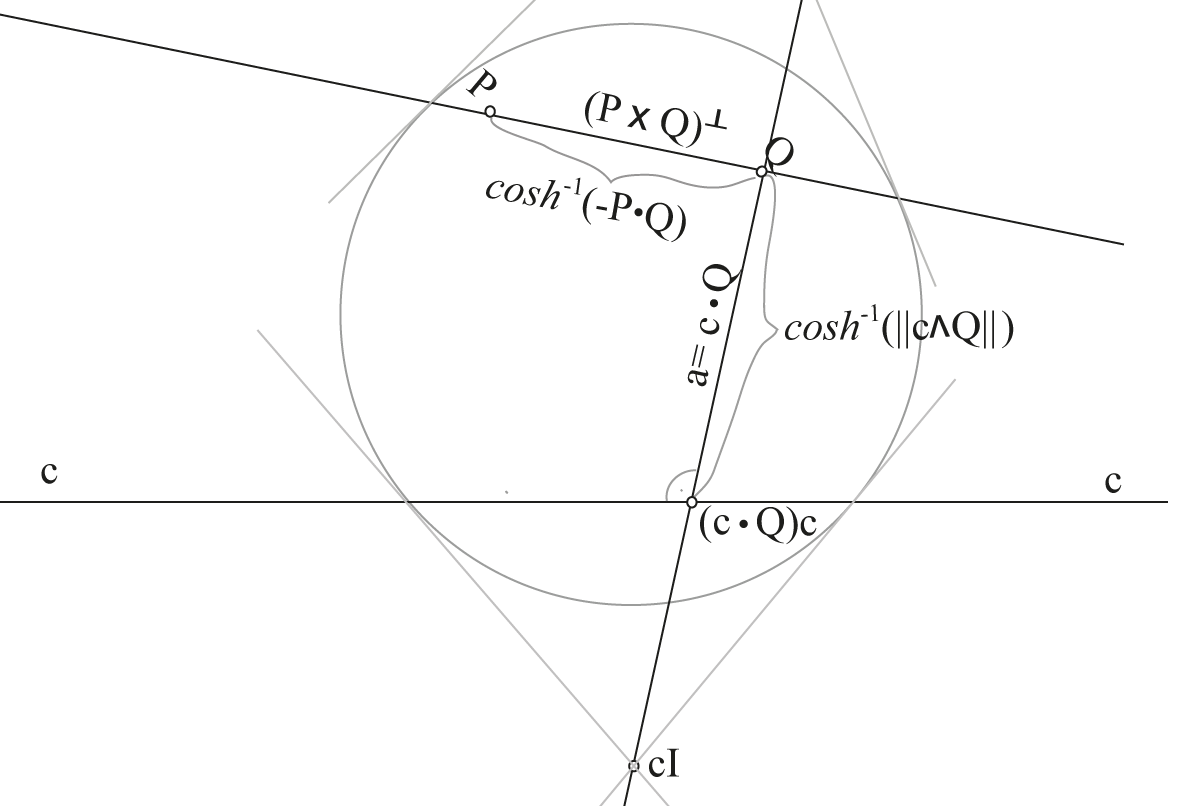
PGA: 2-way products
Product of two proper points \(\mathbf{P}, \mathbf{Q}\). Then
$$\mathbf{P}\mathbf{Q}=\cosh(d)+\sinh(d)\mathbf{R}$$
\(d\) is the distance between the two points and \(\mathbf{R}\) is the normalized form of \(\langle \mathbf{P}\mathbf{Q}\rangle_2\), which is the polar point \((\mathbf{P}\vee\mathbf{Q})^\perp\).

Clifford's geometric algebra
0-vector
2-vector
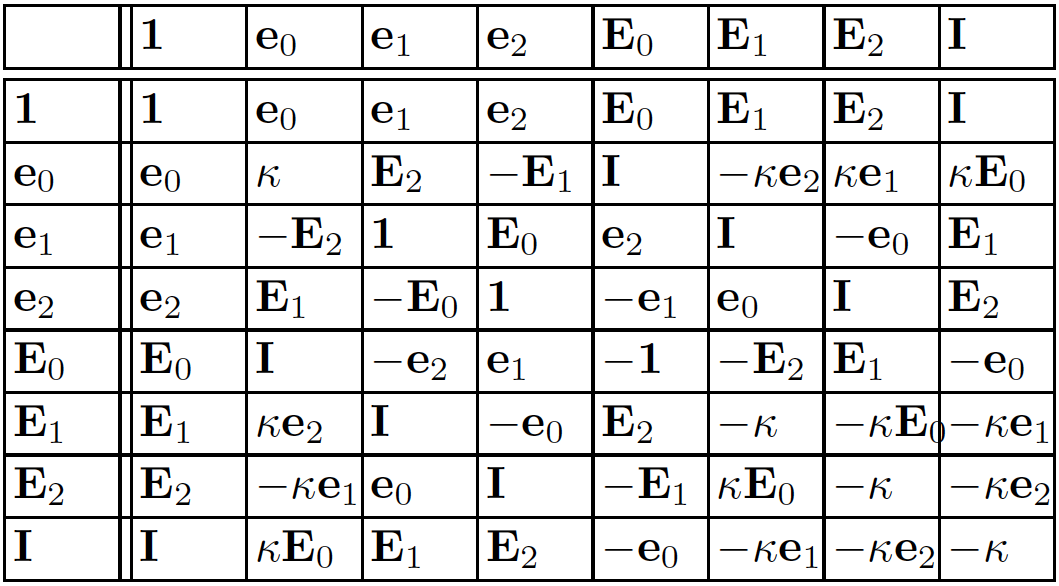
Multiplication table for 2D PGA. \(\kappa \in \{-1,0,1\}\)
2D PGA Preliminaries
1. We can normalize a proper line \(\mathbf{m}\) or point \(\mathbf{P}\) so that:$$\mathbf{m}^2 = 1,~~~\mathbf{P}^2 = -\kappa$$
1a. Elements such that \(\mathbf{x}^2=0\) are called ideal.
1b. Formulas given below often assume normalized arguments.
Isometries via 3-way products
Reflections
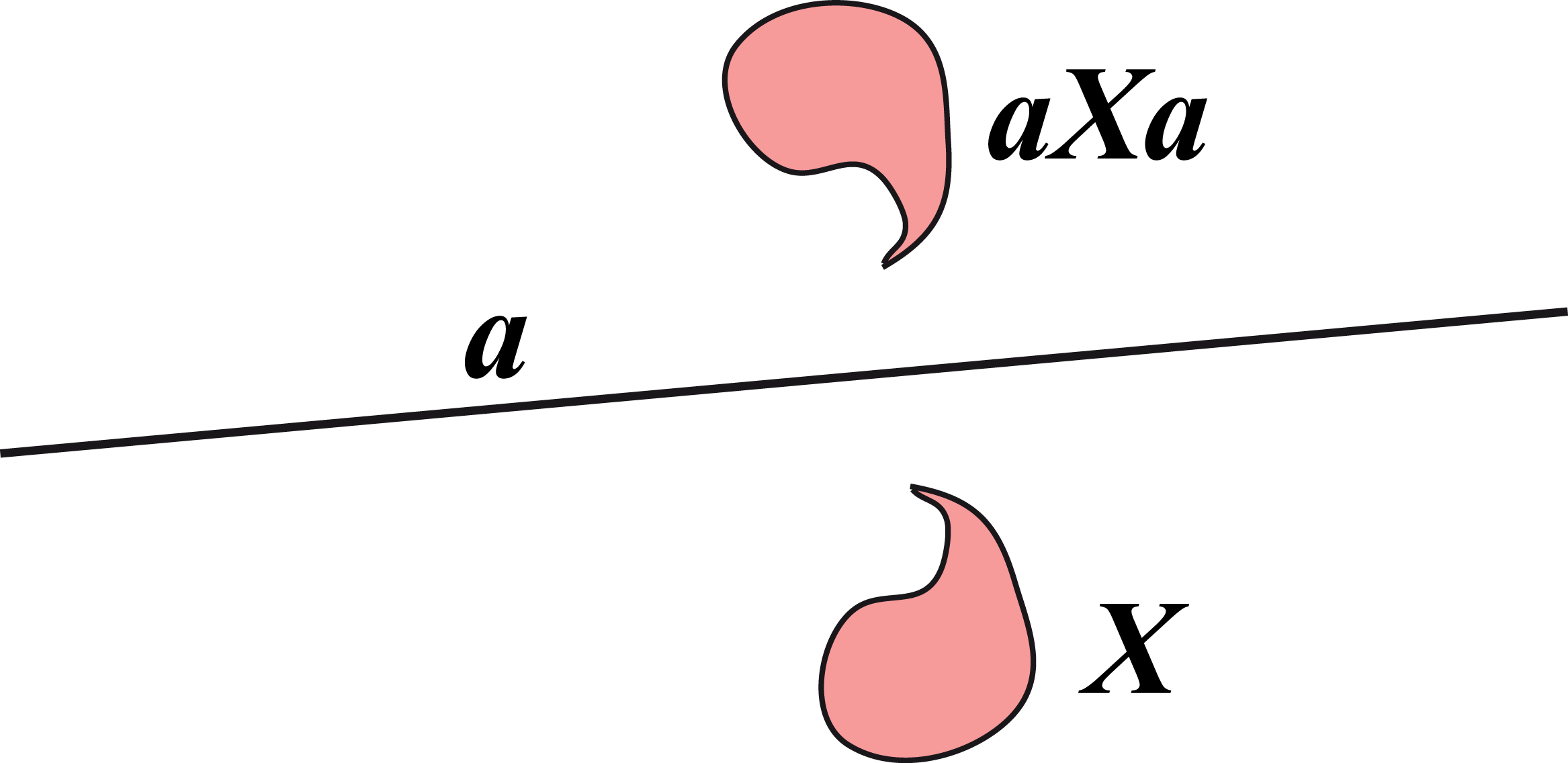
Consider the 3-way product \(\mathbf{X}'=\mathbf{a}\mathbf{X}\mathbf{a}\), where \(\mathbf{a}\) is a proper line and \(\mathbf{X}\) is anything.
Then \(\mathbf{X}'\) is the reflection of \(\mathbf{X}\) in the line \(\mathbf{a}\).
Rotations
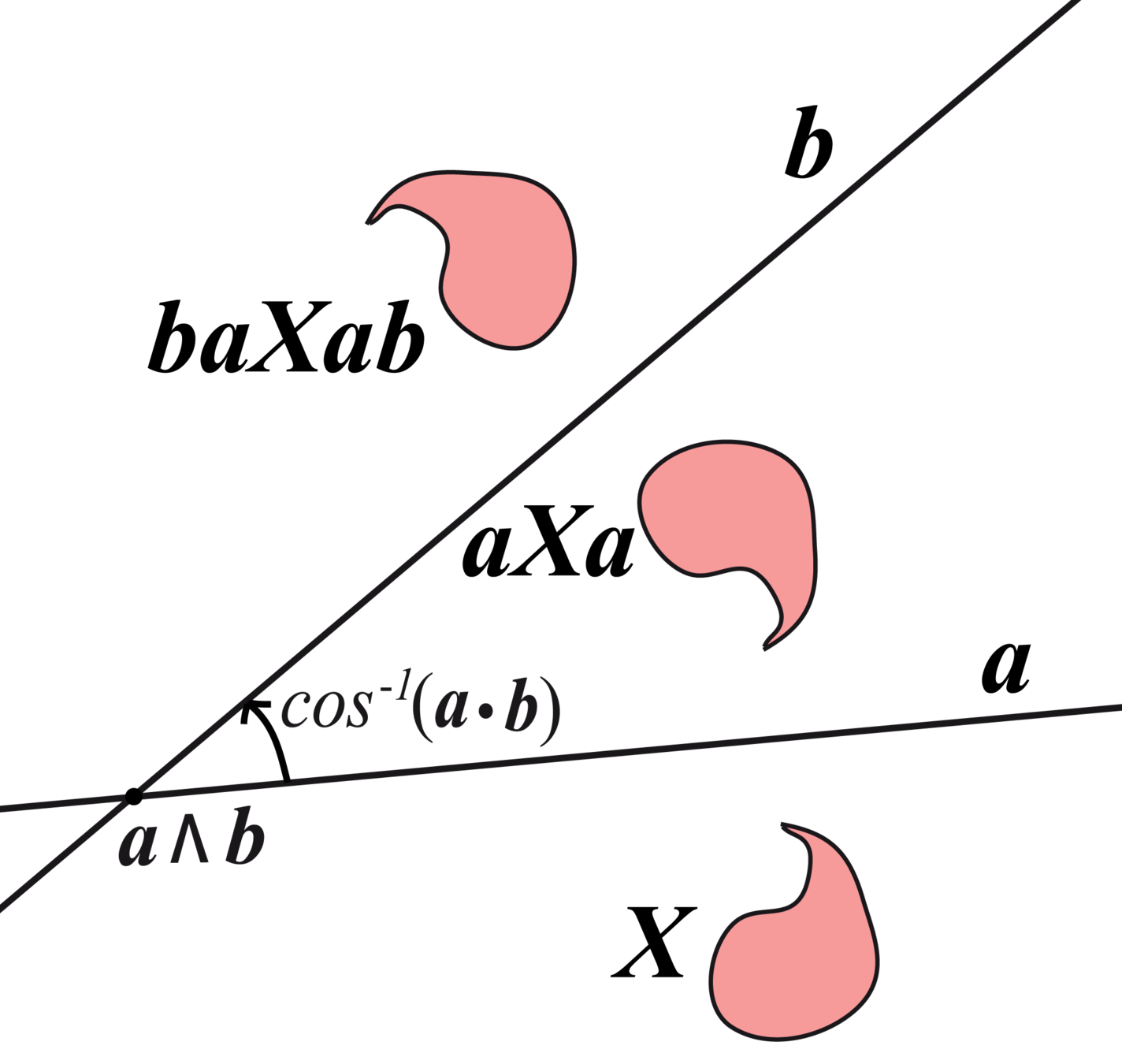
A reflection in a second proper line \(\mathbf{b}\) gives \(\mathbf{X}'=\mathbf{b}(\mathbf{a}\mathbf{X}\mathbf{a})\mathbf{b} = (\mathbf{b}\mathbf{a})\mathbf{X}(\mathbf{a}\mathbf{b})\), by associativity. \(\mathbf{r}:=\mathbf{b}\mathbf{a}\) is called a rotor and \(X'=RX\widetilde{R}\) where \(\widetilde{R}\) is reversal operator.
Isometries via 3-way products
Euclidean translations
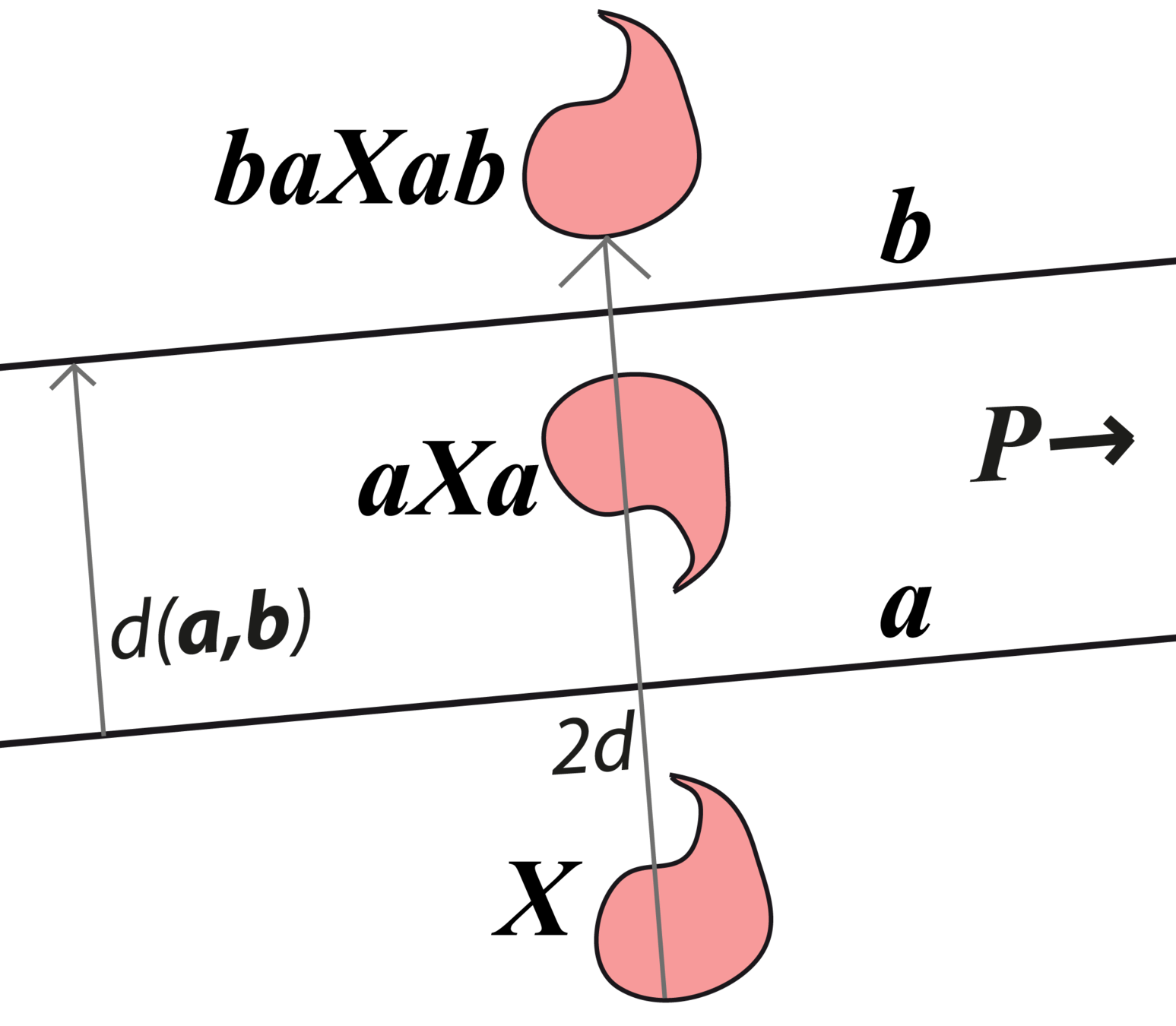
If \(\kappa=0\) and \(\mathbf{P}\) is ideal, \(\mathbf{X}'\) is a translation of distance 2d, where d is the distance betwen a and b. Similar results for \(\kappa = -1\).
Isometries via 3-way products
Quaternions in 2D elliptic PGA
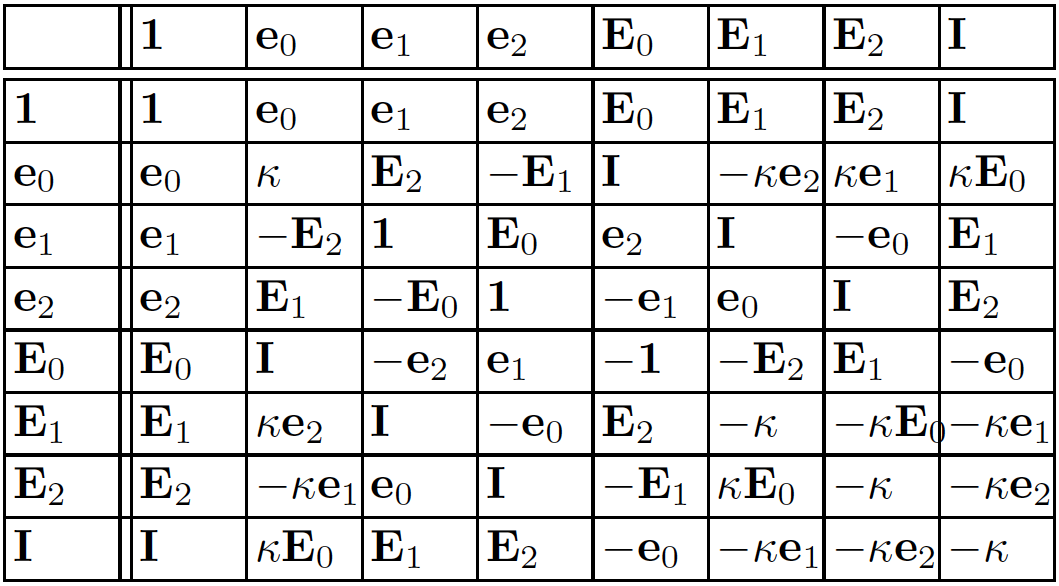
For \(\kappa=1\), the even sub-algebra (shown in red) is isomorphic to \(\mathbb{H}\) under the map $$\{1,\mathbf{E}_0,\mathbf{E}_1,\mathbf{E}_2\}\Leftrightarrow\{1,\mathbf{k},\mathbf{j},\mathbf{i}\}$$
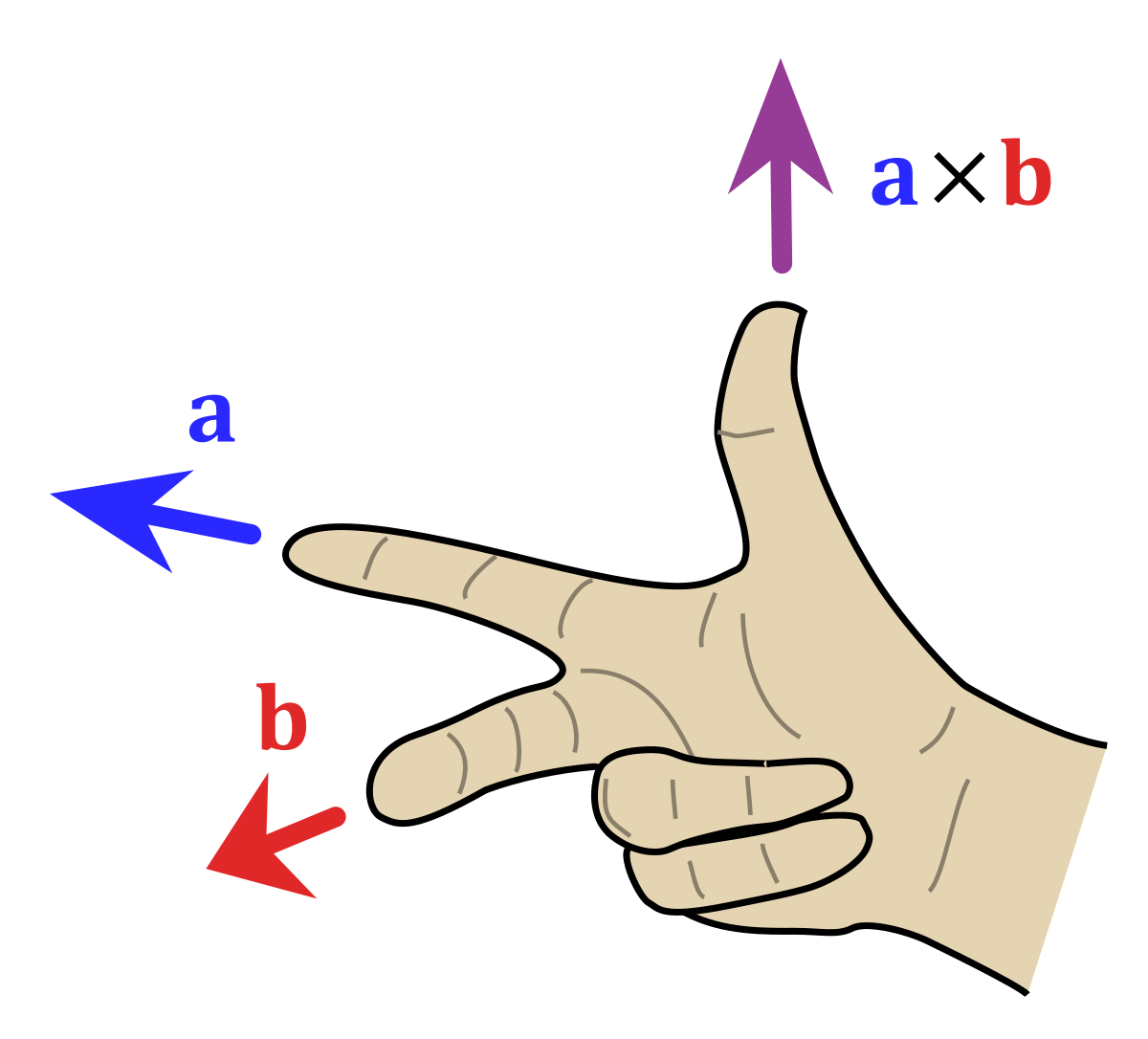
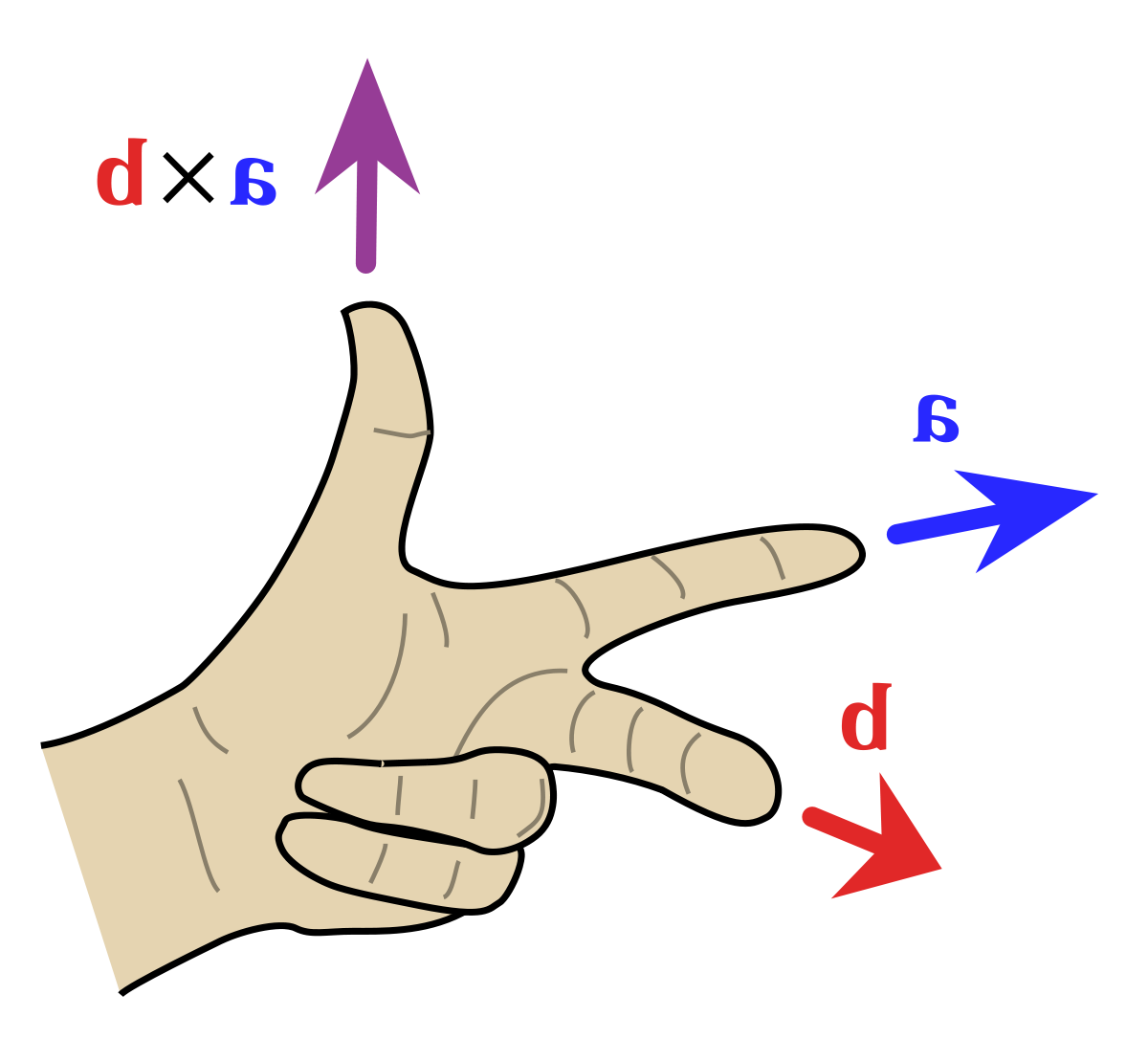
Every rotor can be produced directly by exponentation of a bivector. When \(\mathbf{P}^2=-1\) then
$$\mathbf{r} := \exp(t\mathbf{P}) = \cos(t) + \sin(t)\mathbf{P}$$
\(\mathbf{r}\mathbf{X}\widetilde{\mathbf{r}}\) produces a rotation through angle \(2t\) around \(\mathbf{P}\).
Analogous results hold for \(\mathbf{P}^2=0 \text{ or } 1\) yielding parabolic or hyperbolic isometries.
The ideal norm
\(\mathbf{P}^2 = 0\): how to normalize \(\mathbf{P}\) so \(e^{dP}\) is a translation of 2d? Time permitting ...
Exponentiating bivectors
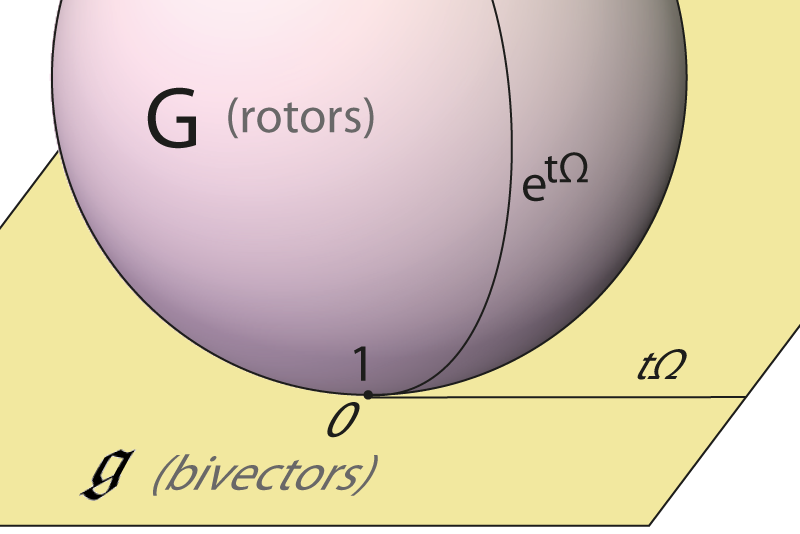
The bivectors \(\bigwedge^2\) form the Lie algebra.
Define \(\mathbf{G}\) to be the elements of the even sub-algebra of norm 1. Then \(\mathbf{G}\) is the Lie group.
And \(\exp: \bigwedge^2 \rightarrow \mathbf{G}\) is a 1:1 map up to multiples of \(2\pi\) (for \(n=3\)).
Lie algebra and Lie group
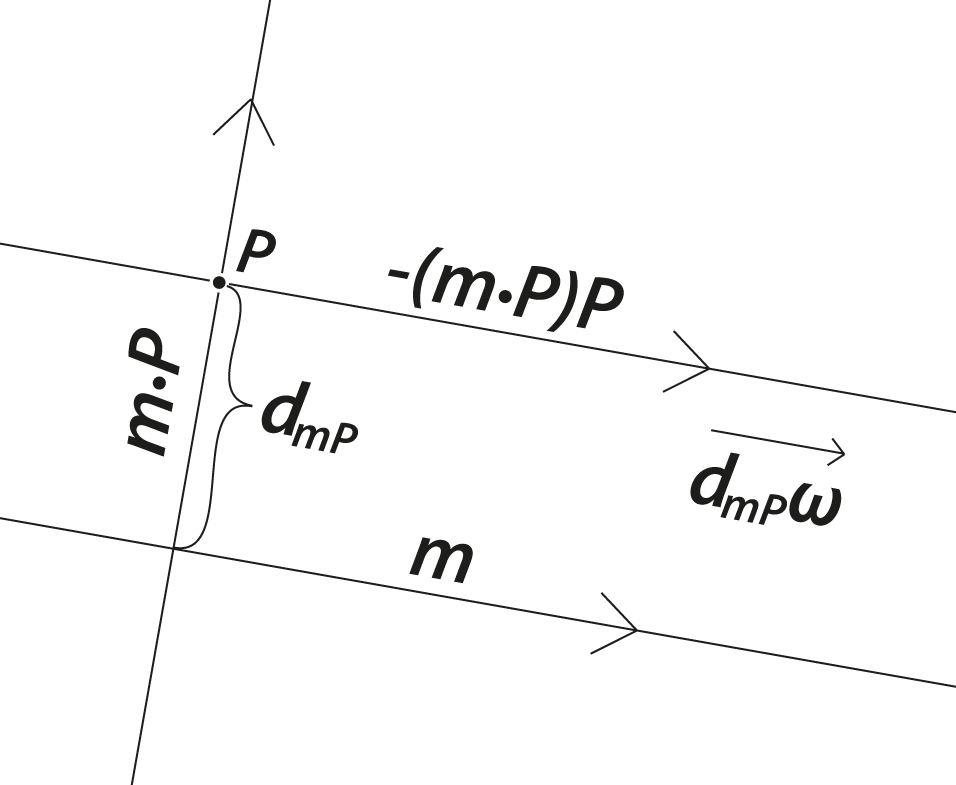
Formula factories via 3-way products
3-way products with a repeated factor of the form \(\mathbf{Y}\mathbf{X}\mathbf{X}\) can be used as formula factories.
Example: \(\mathbf{m} = \mathbf{m}(\mathbf{n}\mathbf{n}) = (\mathbf{m}\mathbf{n})\mathbf{n} \) since for a proper line \(\mathbf{n}^2 = 1\) and associativity. This leads to a decomposition of \(\mathbf{m}\) with respect to \(\mathbf{n}\):

$$(mn)n=(\cos(\alpha)+\sin(\alpha)\mathbf{P})n$$
$$=\cos(\alpha)n + \sin(\alpha)Pn$$
$$=\cos(\alpha)n +\sin(\alpha)P\cdot n$$
$$=\cos(\alpha)n - \sin(\alpha)n\cdot P$$
The arrows show the orientation of the lines.
Formula factories via 3-way products
Examples: Anything can be orthogonally decomposed with respect to anything else! For example ...
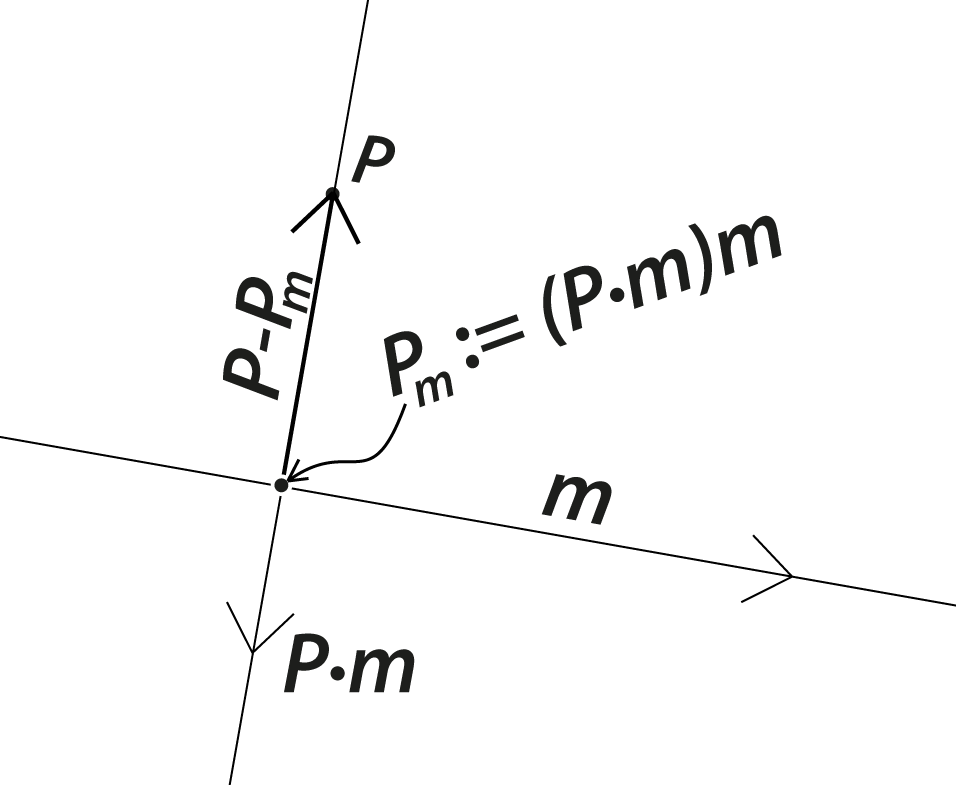
Decompose point WRT line.
Decompose line WRT point.
The pieces of the decomposition are often interesting in their own right. For example, \((P\cdot m)m\) is closest point to \(P\) on \(m\).
Formula factories via 3-way products
General 3-way products \(\mathbf{a}\mathbf{b}\mathbf{c}\) of 1-vectors provide a useful framework for a general theory of triangles. Lots left to do!
Bivectors!

Julius Pluecker
Glimpse at 3D
Glimpse at 3D
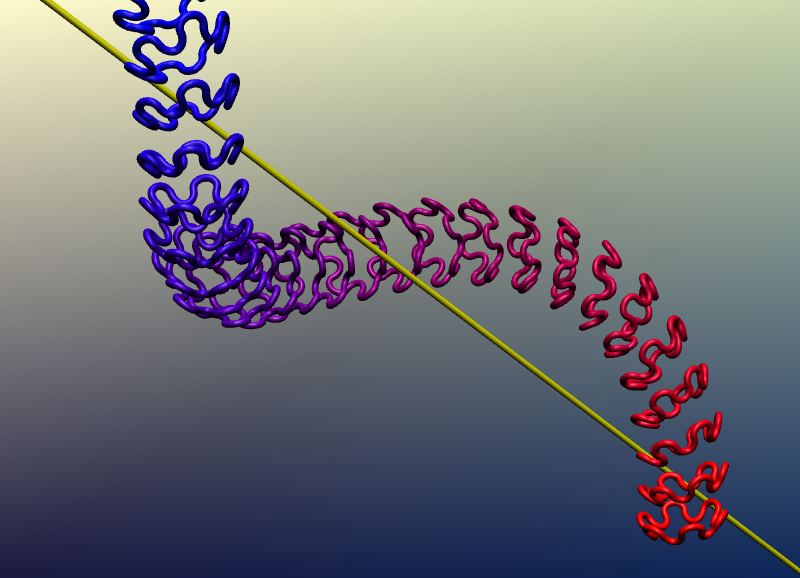
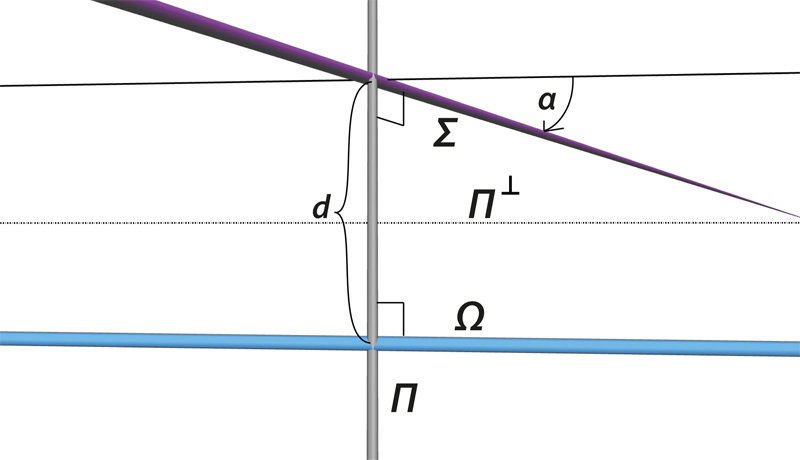

Kinematics and Mechanics
A velocity state is \( \mathbf{V} \in \bigwedge^2\) (in this case a point)
A momentum state is \(\mathbf{M} \in \bigwedge^{n-2}\) (in this case a line)
A rigid body is a collection of Newtonian mass points.
Calculate inertia tensor \(A\) for the body, a quadratic form determined by the mass distribution.
\(\mathbf{M}=A\mathbf{V}\)
ODE's for free top:
PGA equations for the free top in \(P(\mathbb{R}^*_{\kappa})\):
$$\dot{\mathbf{g}} = \mathbf{g} \mathbf{V}~~~~~~~~$$ $$~~~~~~~~~~~ \dot{\mathbf{M}} = \frac12(\mathbf{V}\mathbf{M} - \mathbf{M} \mathbf{V}) $$
where \(\mathbf{g} \in \mathbf{G}\), and \(\mathbf{M}\) and \( \mathbf{V} \)are in the body frame.
2D Kinematics and Mechanics
Advantages of PGA:
- Euclidean case: No splitting into linear and angular parts. A linear velocity is a velocity carried by an ideal point (euclidean). An angular momentum (or force couple) is one carried by the ideal line.
- Similar results hold in 3D.
- The equations are numerically optimal compared to matrix methods. Normalizing \(\mathbf{g}\) keeps it on the solution space.
2D Kinematics and Mechanics
3D Kinematics and Mechanics
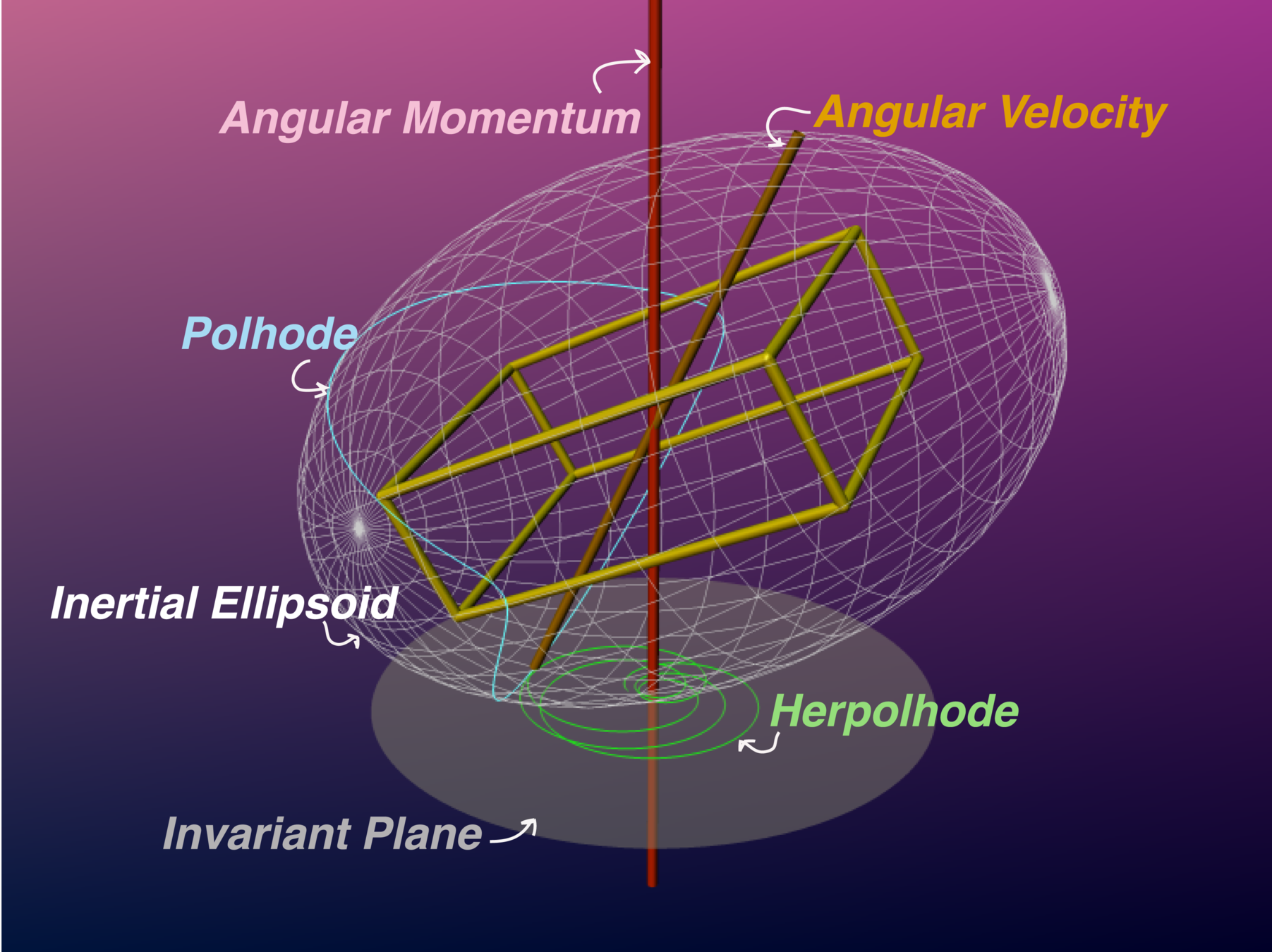

3D Euler top using 3D line geometry
Coordinate-free
Uniform rep'n for points, lines, and planes
Cayley-Klein programmer's wish list

Single, uniform rep'n for isometries
Parallel-safe meet and join operators
Compact expressions for classical geometric results
Physics-ready
Metric-neutral
Backwards compatible
Conclusions
- Dual PGA fulfills the "programmers wish list" from the beginning.
- It completes Clifford's project (cut short by his death) of combining Grassmann algebra with all biquaternions, not just the elliptic ones.
- There's a lot left to explore, both in non-euclidean and euclidean, 2D and 3D.
- Team members sought to create browser-based metric-neutral PGA scene graph with physics engine.
- Ask me about ideal norms and dual euclidean space.
Resources


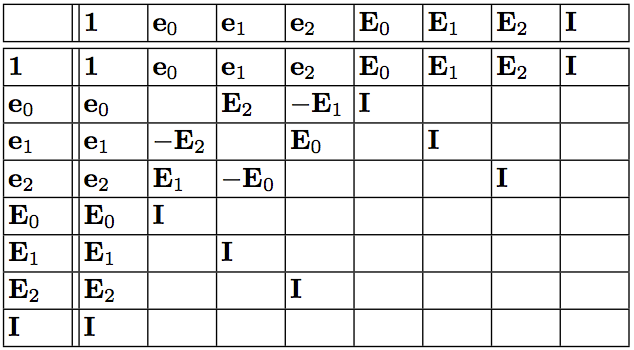
Dual projective Grassmann algebra
Multiplication table for \(\bigwedge\mathbb{R}P^{2\large{*}}\)
Geometric algebra notation
- General multivector is sum of k-vectors: \(\mathbf{a} = \mathbf{\Sigma}_k\langle \mathbf{a}\rangle_k\)
- Points are large letters (\(\mathbf{P}\)) and lines are small (\(\mathbf{m}\)).
- The unit pseudoscalar is written \(\mathbf{I}\).
- The product of a k-vector and an m-vector is a sum $$\mathbf{K}\mathbf{M} = \mathbf{\Sigma}_{i=|k-m|}^{k+m}\langle \mathbf{K}\mathbf{M}\rangle_i$$ where i increases by steps of 2.
- \(\mathbf{K}\wedge\mathbf{M} = \langle \mathbf{K}\mathbf{M}\rangle_{k+m} \)
- \(\mathbf{K}\cdot\mathbf{M} := \langle\mathbf{K}\mathbf{M}\rangle_{|k-m|}\)
- \(\mathbf{K}\times\mathbf{M} := \mathbf{K}\mathbf{M}-\mathbf{M}\mathbf{K}\)
- \(\mathbf{K}\vee\mathbf{M}\) is the join.
The euclidean algebra \(\mathbf{P}(\mathbb{R}^*_{2,0,1}) \)
Question: Why is the signature \((2,0,1)\) using the dual construction the proper model for the euclidean plane?

Answer: Given two lines \(\mathbf{m}_i = c_i\mathbf{e}_0+a_i\mathbf{e}_1+b_i\mathbf{e}_2\) (with equations \(a_ix+b_iy+c_i=0\)). Then $$\mathbf{m}_1\cdot\mathbf{m}_2=c_0c_1\mathbf{e}_0^2+a_1a_2\mathbf{e}_1^2+b_1b_2\mathbf{e}_2^2$$ Since the cosine of the angle between the lines is \(a_1a_2 + b_1b_2\), \(\mathbf{e}_0^2=0\) while \(\mathbf{e}_1^2=\mathbf{e}_2^2=1\).
The euclidean algebra \(\mathbf{P}(\mathbb{R}^*_{2,0,1}) \)
Question: Why is the signature \((2,0,1)\) using the dual construction the proper model for the euclidean plane?
Answer: Given two lines \(\mathbf{m}_i = c_i\mathbf{e}_0+a_i\mathbf{e}_1+b_i\mathbf{e}_2\) (with equations \(a_ix+b_iy+c_i=0\)). Then $$\mathbf{m}_1\cdot\mathbf{m}_2=c_0c_1\mathbf{e}_0^2+a_1a_2\mathbf{e}_1^2+b_1b_2\mathbf{e}_2^2$$ Since the cosine of the angle between the lines is \(a_1a_2 + b_1b_2\), \(\mathbf{e}_0^2=0\) while \(\mathbf{e}_1^2=\mathbf{e}_2^2=1\).
History: That \(\mathbf{P}(\mathbb{R}^*_{2,0,1}) \) models euclidean geometry was first published by Jon Selig in 2000.