- Linhas principais de curvatura
- Linhas geodésicas
- Linhas Assintóticas
Nesta aula iremos estudar:
A área da matemática que estuda estas linha chama-se Geometria Diferencial.
Como não entraremos no mundo do cálculo e suas equações diferenciais, o título mais adequado para a nossa aula é...
- Linhas principais de curvatura
- Linhas geodésicas
- Linhas assintóticas
Para entendê-las, primeiro temos que saber o que é, e como medimos a curvatura de:
Geometria Diferencial para Leigos

- uma curva livre no espaço
- uma curva sobre uma superfície
- uma superfície
Apresentamos a história dos sócios
Sr. Arame Curvado Sr. Chapa Torta
Essa história é uma obra de ficção.
Qualquer semelhança com pessoas ou fatos reais é mera coincidência.
Desde o começo, quando ambos eram jovens, o arame já era mais simples e fácil de entender... já o chapa....


Qual é a essência de uma curva?
O que é curvatura?
O que ela mede?
Para responder estas questões, o melhor é nos colocarmos na pele do Sr. Arame...


a curvatura indica o quão rápido a tangente muda de direção .
Como a curvatura é medida?
vetor tangente
plano normal
raio de curvatra
a curvatura é o inverso do raio de curvatura
k = 1/r (pode ser positiva, negativa ou nula)
círculo osculador

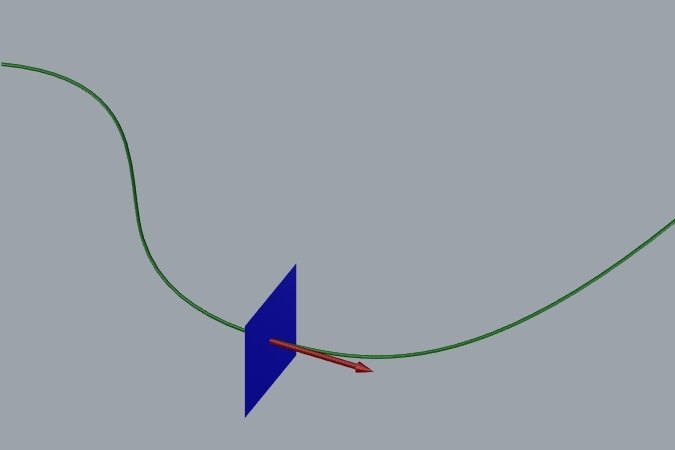
a curvatura é nula em trechos retos e nos pontos de inflexão
(o Rhino tem um comando para desenhar círculos osculadores e outro para mostrar as curvaturas)
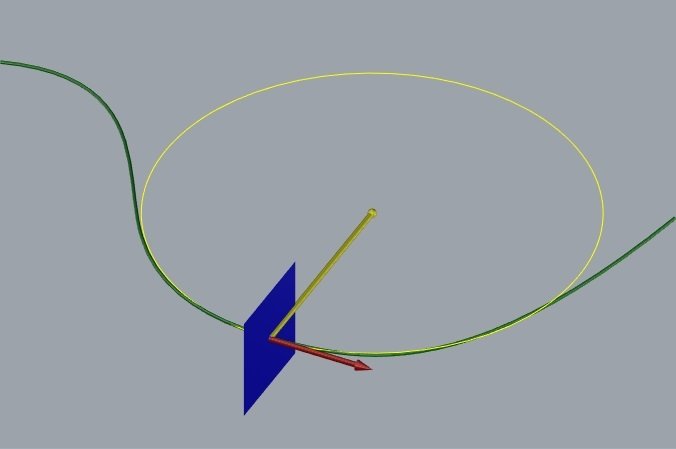
Triedro de Frenet
vetor tangente
plano normal
círculo osculador
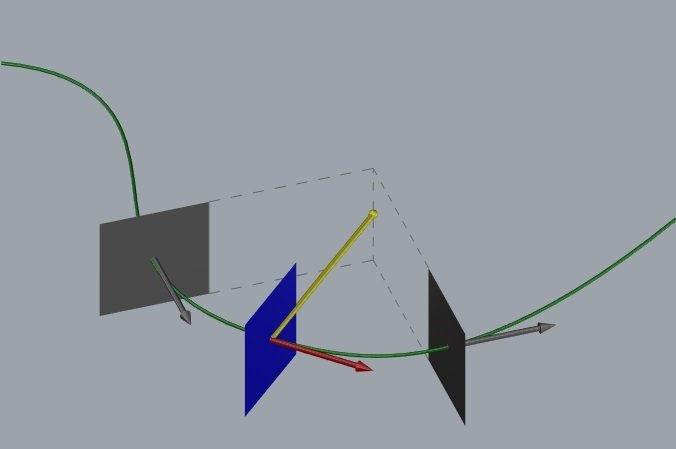
vetor normal principal
vetor binormal
plano osculador
plano retificador
Já uma curva espacial tem curvaturas e torções (a torção mede a velocidade de mudança do plano osculador).
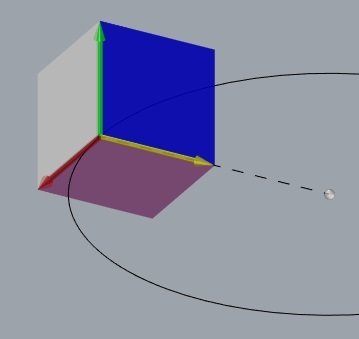
Uma curva plana tem apenas curvaturas.
(a curvatura não muda a direção do plano osculador)
.
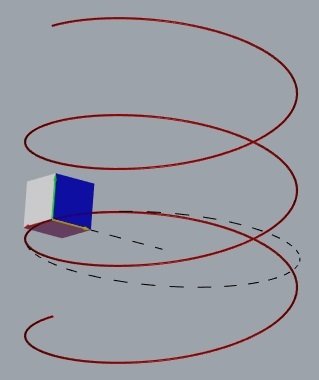
A forma de uma curva espacial é definida pelas curvaturas e torções de seus pontos.
a hélice cilíndrica tem curvatura e torção constantes.

Só isso?
Puxa, como sou simples!
curvatura e continuidade


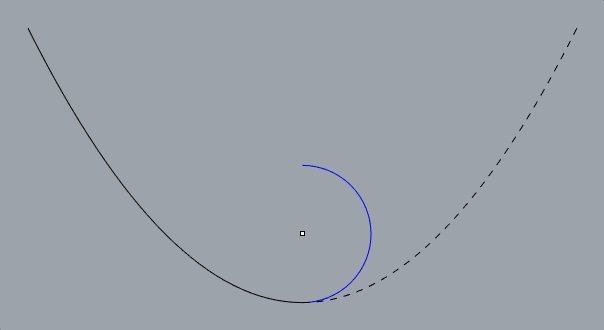



evoluta
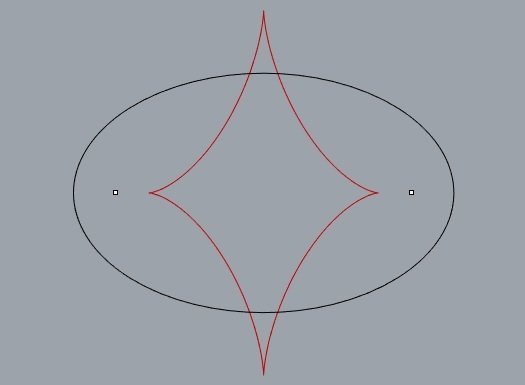
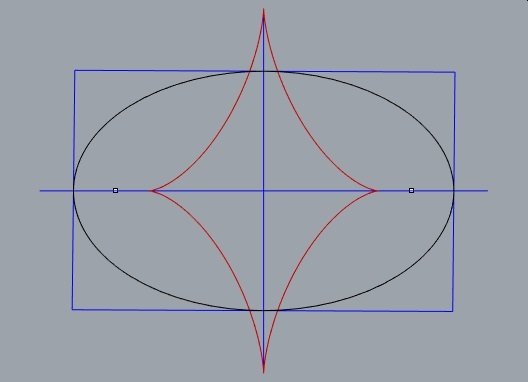
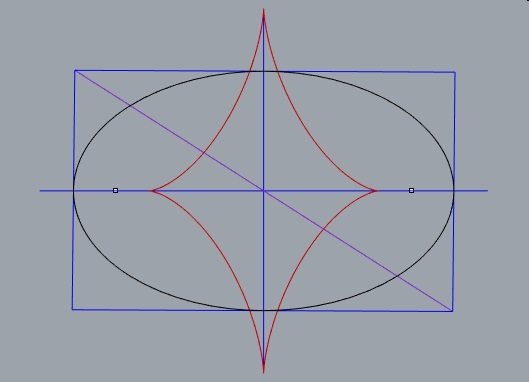
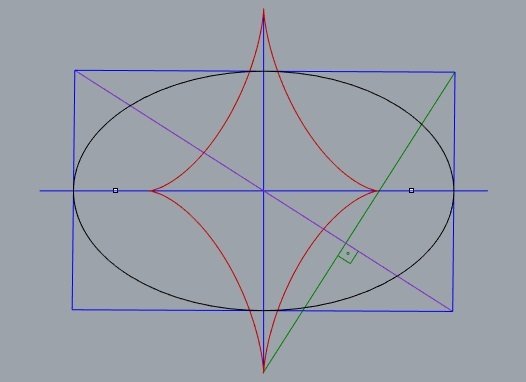
é a curva formada pelos centros de curvatura.
evoluta da elipse
Sozinho não consigo me entender...
Alguém pode me ajudar?
Boa tarde senhor.
Posso lhe apresentar a minha tangente?


Tangentes e normais
vetor tangente
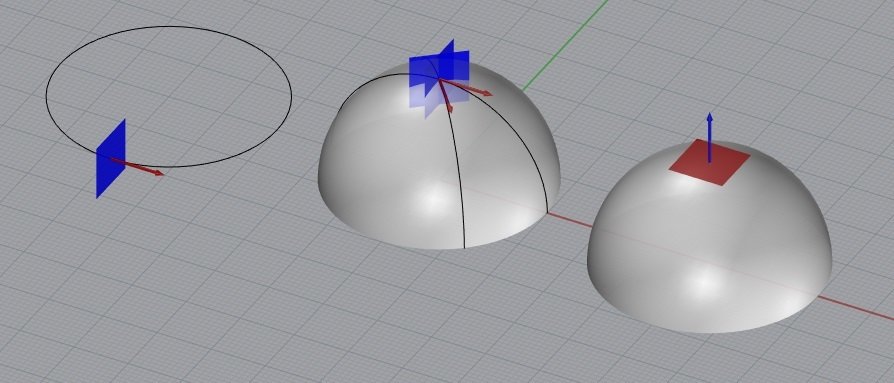
vetor normal
plano normal
plano tangente
em curvas e em superfícies
A sua direção sempre combina nos meus planos...
Podemos ser sócios...
Você concorda com a minha tangente?


Poucos anos depois...
Obrigado, sou apenas um cara muito normal. Principalmente nesta direção...
Isso não é normal, no meu plano, normal é ir para cima...
Vamos ver quem manda aqui!!

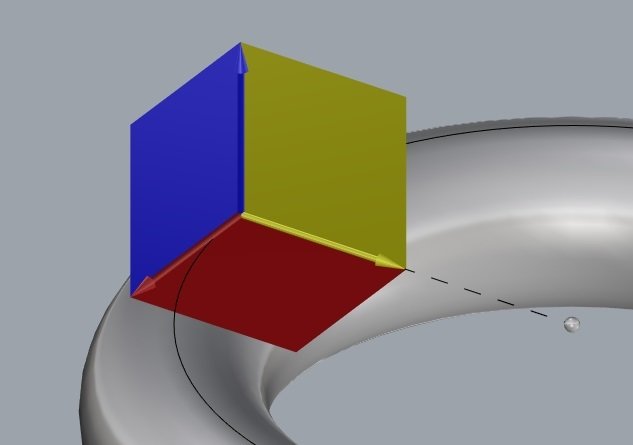


Arame, você é um ótimo diretor!
Darboux frame
Frenet frame
normal
normal
Então três auxiliares são contratados.
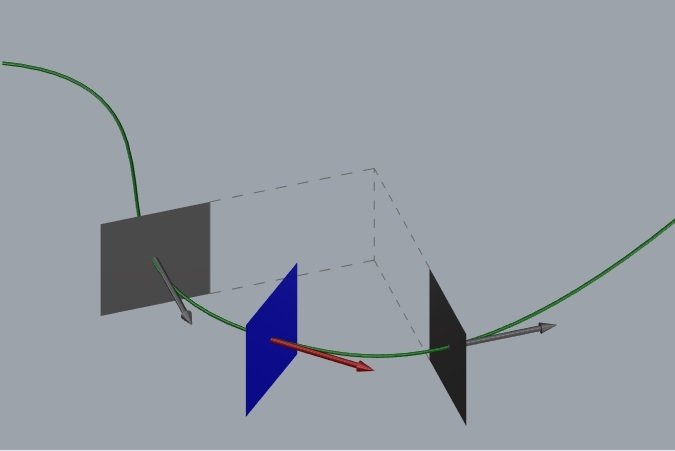
- o primeiro é a projeção do arame no plano vertical do chapa. A curvatura dessa projeção chama-se curvatura normal (kn). É o empregado preferido do Sr. Chapa pois a normal de ambos coincide .
- o segundo é a projeção do arame no plano tangente do chapa. A curvatura dessa projeção chama-se curvatura geodésica (kg). Ele sempre discorda do Sr. Chapa em relação a normal.
- o terceiro chama-se torção geodésica, acrescenta a variação entre as normais dos sócios. (tg= t+var)
Triedro de Darboux
vetor normal
vetor tangente
vetor tangente normal
plano tangente
curva sobre a superfície
U
N
T
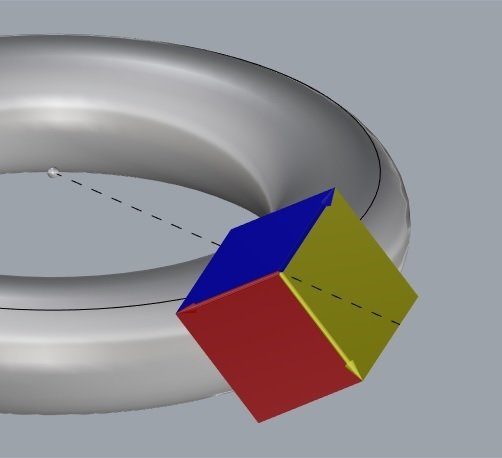
normal principal
(da curva)
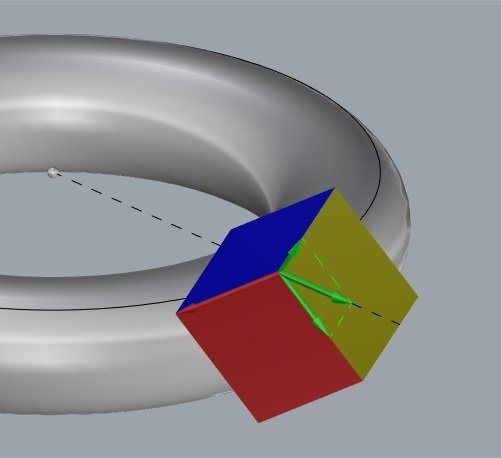
k
kn
kg
Gostei do curvatura normal... ele sabe das coisas...
Já o curvatura geodésica, se não for necessário, ponho no olho da rua...
na nossa sociedade minha curvatura se decompôs em duas e a torção mudou.
Isso é inaceitável, estou fora!!!


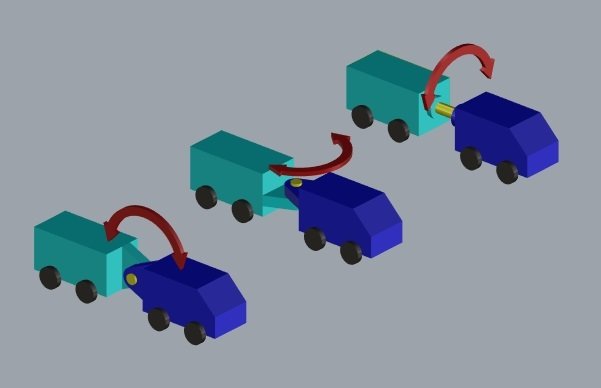
Quando uma linha está associada a uma superfície, ela herda a direção normal desta.

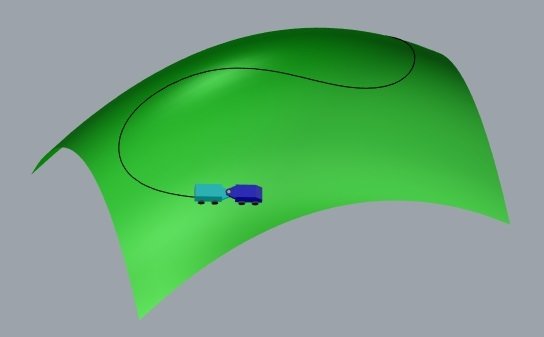
Se a curvatura da estrada for apenas na "horizontal" (plano tangente), o motorista do carrinho vira o volante para fazer a curva (curvatura geodésica).
Se a curvatura for apenas na "vertical" (vetor normal), o motorista não vira o volante e o carro sobe e desce, seguindo as concavidades do terreno (curvatura normal).
Se a curvatura se der nas duas direções, ela é decomposta em curvatura normal e curvatura geodésica.
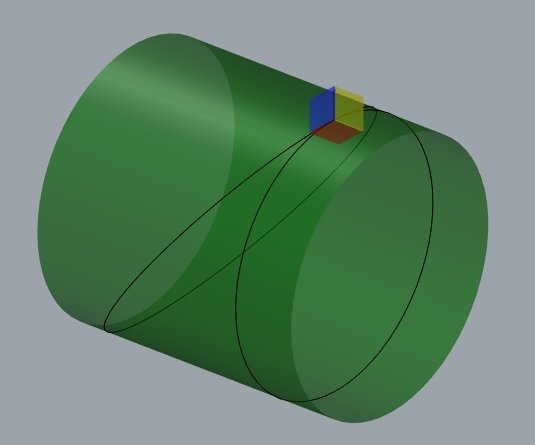
Todas as trajetórias que passam por um ponto com a mesma tangente, tem a mesma curvatura normal, mas curvaturas geodésicas distintas.
nossa, a curvatura normal não depende do sócio... sou eu quem a define!
Eu tenho uma curvatura própria!!!!

Então o Chapa experimenta outras sociedades...
curvatura geodésica, você está DEMITIDO!!!
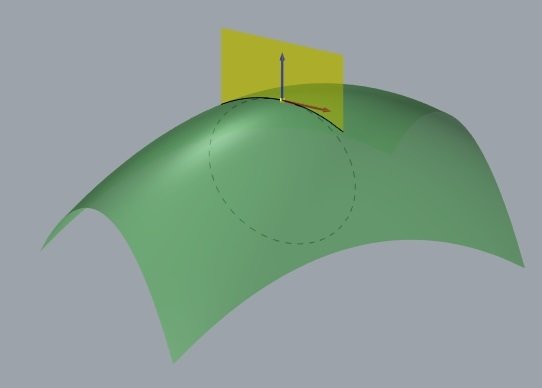
tangente
normal
kn = 1/r
r
Em um ponto de uma superfície, cada direção tem um valor de curvatura normal .
Os valores mínimo (k1) e máximo (k2) são as curvaturas principais e ocorrem nas direções principais que são sempre ortogonais.

Curvatura de Gauss K = k1 x k2
Curvatura Média H = (k1 + k2)/2
K<0 ponto hiperbólico (anticlástico)
K=0 ponto parabólico (desenvolvível)
K>0 ponto elíptico (sinclástico)
H=0 superfície mínima
H=cte CMC (superfície de curvatura média cte)
Curvaturas de uma Superfície
Círculo de Mohr
Fórmula de Euler para cálculo de kn dados k1, k2 e
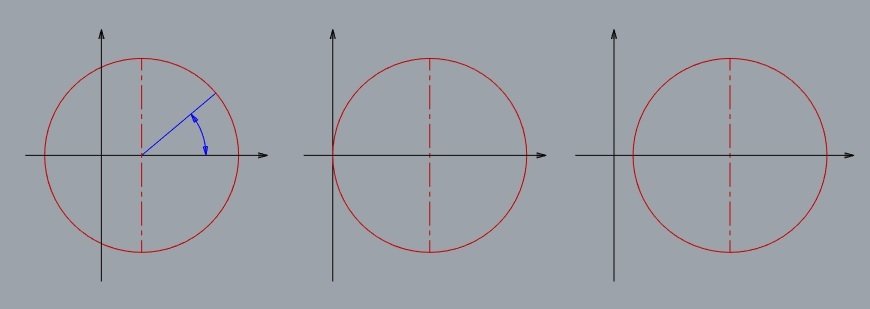
k1
k2
H
H
K<0
K=0
K>0
tg
kn
tg
tg
kn
kn
k1
k2
k1
k2
H
Fórmula para cálculo de tg dados k1, k2 e
Visualizando no Rhino
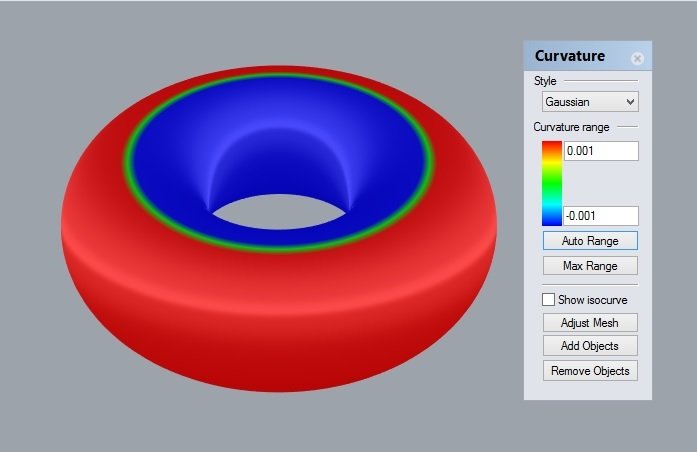
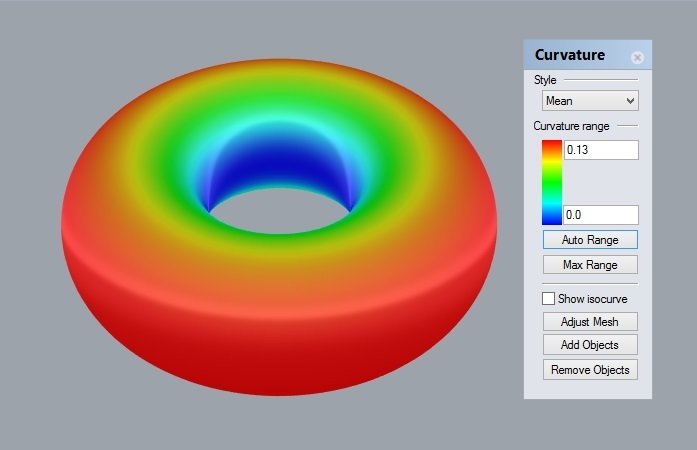
curvatura de Gauss
curvatura média
Teorema Egregium de Gauss
a curvatura gaussiana é invariante sob isometrias locais


Teorema de Ronconi
forma = estrutura


Curvatura de Gauss discreta

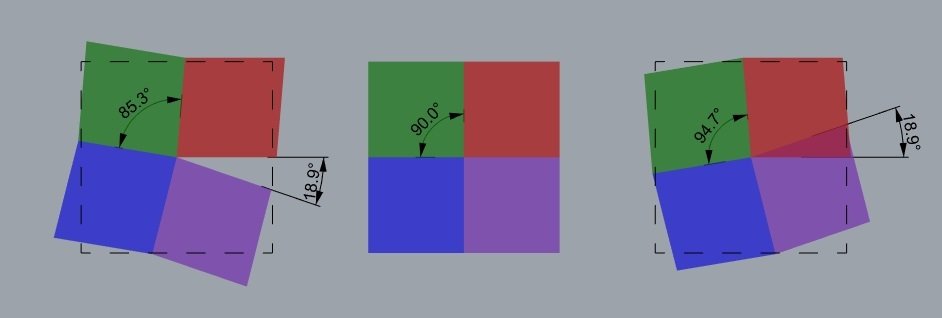
K>0
K=0
K<0
Curvatura de Gauss discreta

Entrelaçamento Triaxial (Kagome)

Soma dos ângulos de um triângulo

Teorema de Descartes para poliedros
A soma dos ângulos faltantes dos vértices de um poliedro fechado e sem furos (topologicamente igual à esfera) é igual a 720°

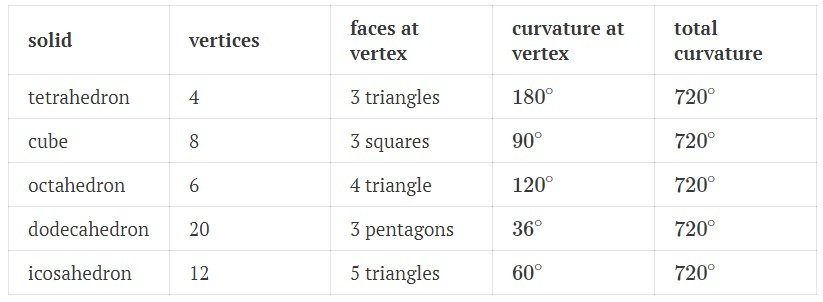
Teorema de Gauss Bonnet
para superfícies fechadas topologicamente igual a esfera

Resumo

Cada ponto de uma curva espacial tem curvatura e torção

Cada ponto de uma curva sobre uma superfície tem curvatura normal, curvatura geodésica e torção geodésica

Cada ponto de uma superfície tem curvatura de Gauss e curvatura média
Agora já temos o conhecimento básico necessário para estudarmos as tão esperadas:
- Linhas principais de curvatura
- Linhas geodésicas
- Linhas Assintóticas
curvatura normal
curvatura geodésica
torção
geodésica
Linhas principais de curvatura tem torção geodésica = 0
Linhas geodésicas tem curvatura geodésica = 0
Linhas assintóticas tem curvatura normal = 0

curvatura normal
curvatura geodésica
torção
geodésica
tem torção geodésica =0
Linhas Principais de Curvatura
Direções principais de curvatura
k2 = máxima curvatura normal
k1 = mínima curvatura normal

são as direções onde as curvaturas normais são máximas e mínimas
as linhas principais de curvatura seguem estas direções
e são sempre ortogonais (90°)
Direções principais de curvatura na esfera

A curvatura normal é a mesma em qualquer direção (k1 = k2).
Qualquer linha sobre uma esfera é uma linha principal de curvatura.
Linhas principais de curvatura
em superfícies de revolução
são os meridianos e os paralelos.

pontos umbílicos são pontos onde k1=k2
(a superfície é localmente esférica)
pelas intersecções de superfícies triortogonais
Linhas principais de curvatura


ponto umbilico

na esfera todos os pontos são umbílicos
Linhas principais de curvatura
em uma superfície qualquer
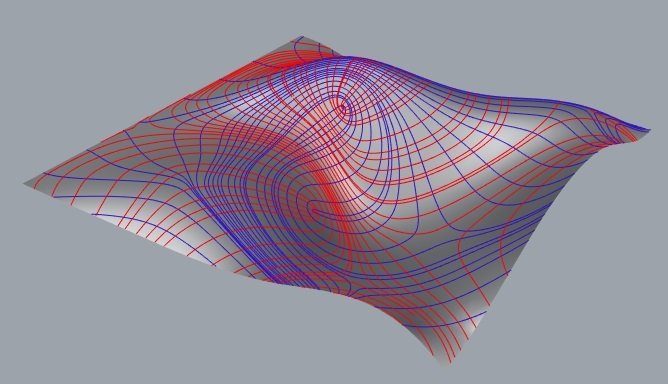
São traçadas por programas de computador.
(formiguinhas que seguem as direções principais)

Por um ponto não umbílico passam apenas 2 linhas principais de curvatura
Linha Principal de Curvatura
As superfícies tangente e normal a uma linha de superfície, são desenvolvíveis (K=0) se, e somente se, esta linha for uma linha principal de curvatura.

superfície normal
superfície tangente
Linhas Principais de Curvatura na arquitetura


pavilhão no 1° piso da Torre Eiffel
2005 - Buro Happold
Roppongi Canopy - Tokyo

curvatura normal
curvatura geodésica
torção
geodésica
tem curvatura geodésica =0
Linhas Geodésicas



Um carrinho que não vira para o lados, ao andar sobre uma superfície, percorre linhas geodésicas.
Uma fita adesiva aplicada sobre uma superfície, sem forçar curvas laterais , percorre linhas geodésicas.
por um ponto passam infinitas linhas geodésicas.
Na esfera, as linhas geodésicas são grandes círculos (meridianos, equador).

Um veículo de duas rodas percorre uma linha geodésica apenas quando a rotação de ambas as rodas forem iguais.
Em cada ponto de uma curva geodésica, a normal da superfície coincide com a normal principal da curva.
Então temos:
Essa curva sabe o que é normal...

kg = 0
kn = k
tg = t
Ou seja, uma curva geodésica tem os mesmos valores de curvatura e torção da curva solta no espaço.
Uma geodésica só é plana se for uma linha principal de curvatura.

No cilindro, as linhas geodésicas são hélices, circunferências e retas.
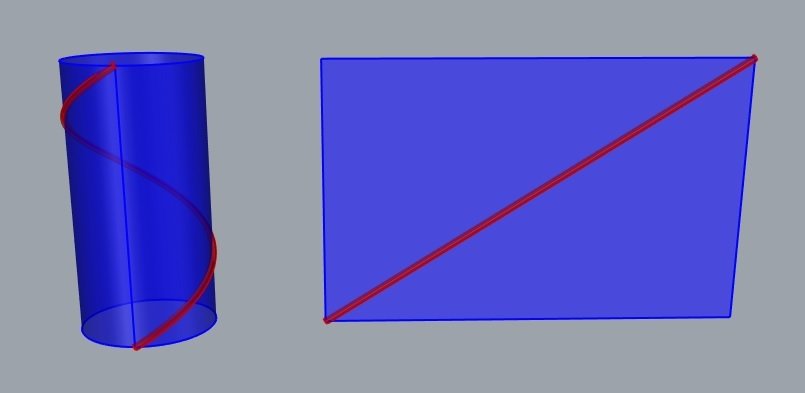
- Linhas geodésicas de superfícies desenvolvíveis, viram retas na planificação.
- A linha geodésica, localmente, é o caminho mais curto entre 2 pontos da superfície.
- Uma curva geodésicas só é plana se for uma linha principal de curvatura.
teto com ripas seguindo linhas geodésicas
Linhas Geodésicas


curvatura normal
curvatura geodésica
torção
geodésica
tem curvatura normal =0
Linhas Assintóticas
linhas assintóticas são percorridas por "formiguinhas" que seguem nas direções cuja curvatura normal é igual a zero.

em qual direção kn =0 ?
Fórmula de Euler para cálculo de kn dados k1 e k2
Quantas linhas assintóticas passam por um ponto?
- pontos anticásticos K<0 tem duas direções assintóticas
- pontos desenvolvíveis K=0 tem apenas uma direção assintótica
- pontos sinclásticos K>0 não tem direções assintóticas
Linhas assintóticas em regiões anticlásticas (K<0)
- por cada ponto passam duas linhas assintóticas.
- as linhas podem ser retas os curvas
- as linhas assintóticas não são linhas principais de curvatura.
regiões sinclásticas (K>0) não tem linhas assintóticas.
Em cada ponto de uma curva assintótica, a normal da superfície discorda em 90° com a normal principal da curva.

Discordamos o máximo possível.

Superfícies Regradas Anticláticas (K<0)
(não são desenvolvíveis)
O paraboloide hiperbólico e o hiperboloide de 1 folha são as únicas superfícies com as duas linhas assintóticas retas.


o ângulo de cruzamento das retas variam de um cruzamento para o outro.
- por cada ponto passam duas linhas assintóticas.
- ao menos uma delas é reta.
- não são linhas principais de curvatura.
Superfícies Regradas Anticláticas (K<0)
(não são desenvolvíveis)
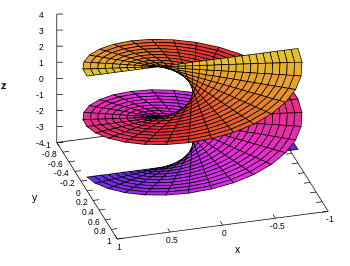
É a única superfície mínima regrada.
As linhas assintóticas se cruzam a 90°.
O helicoide tem uma linha assintótica reta e outra curva.
- por cada ponto passa apenas uma única linha assintótica.
- a linha assintótica é reta, também é uma linha geodésica e também é uma das linhas principais de curvatura.
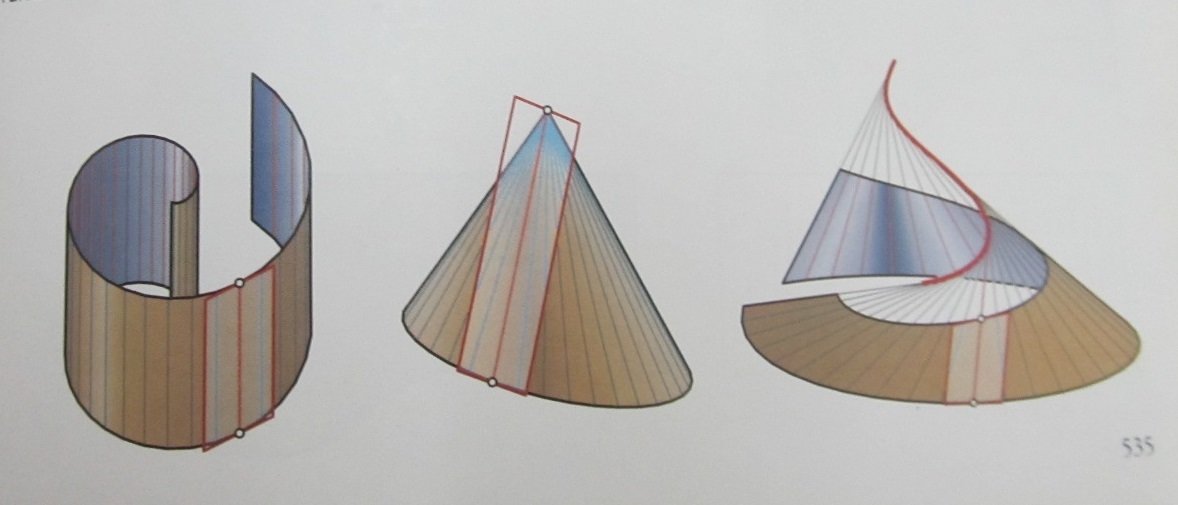
Superfícies (Regradas) Desenvolvíveis (K=0)
Superfícies Mínimas
curvatura média H = (k1+k2)/2 = 0
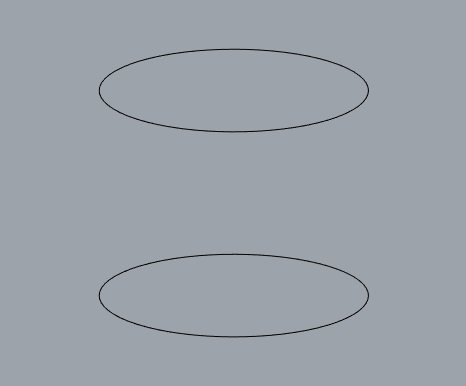
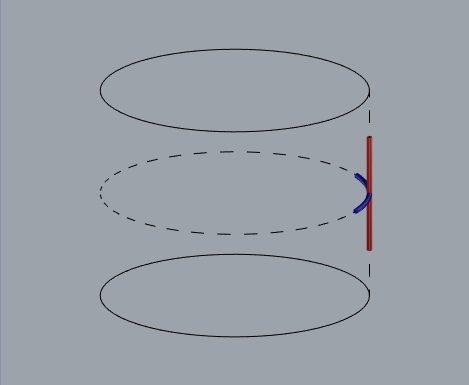

k1 = -k2
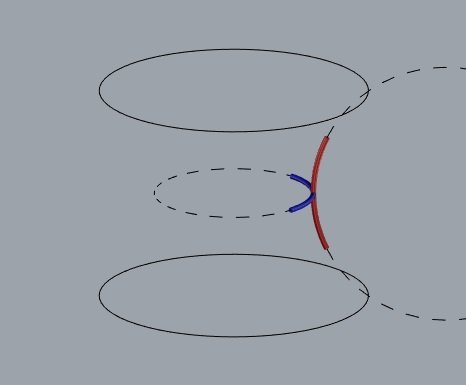
catenóide
Qual é a superfície de menor área que liga as duas circunferências?
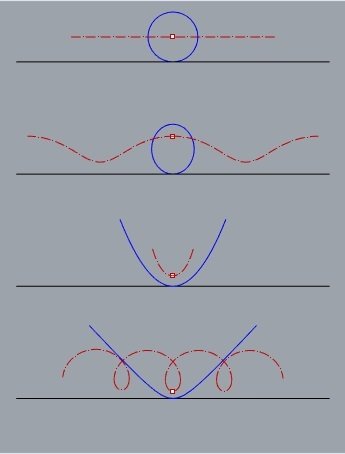
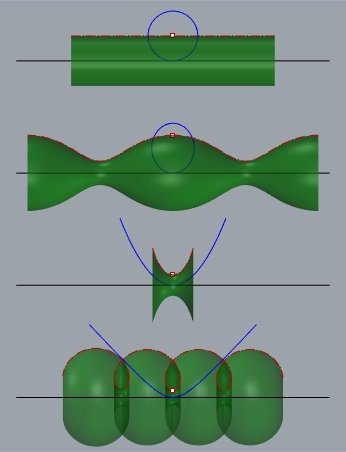
Superfícies de Delaunay
(CMC de revolução)
onduloide
cilindro
catenoide (H=0)
nodoide
círculo
elipse
parábola
hipérbole
Charle Eugène Delaunay



curvatura média constante
A máxima altura de um catenóide é de 66,3% do diâmetro da borda circular.
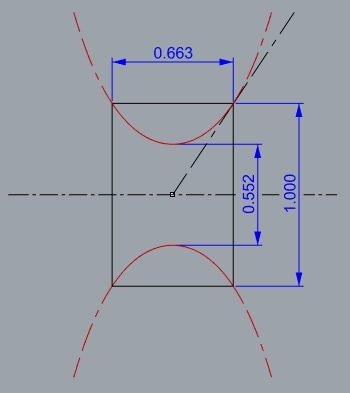
película de sabão (soap film)
Superfícies Mínimas Famosas
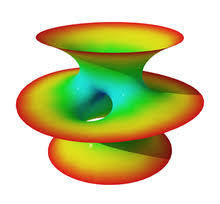
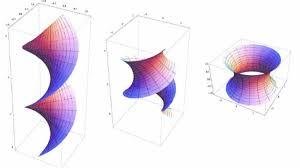

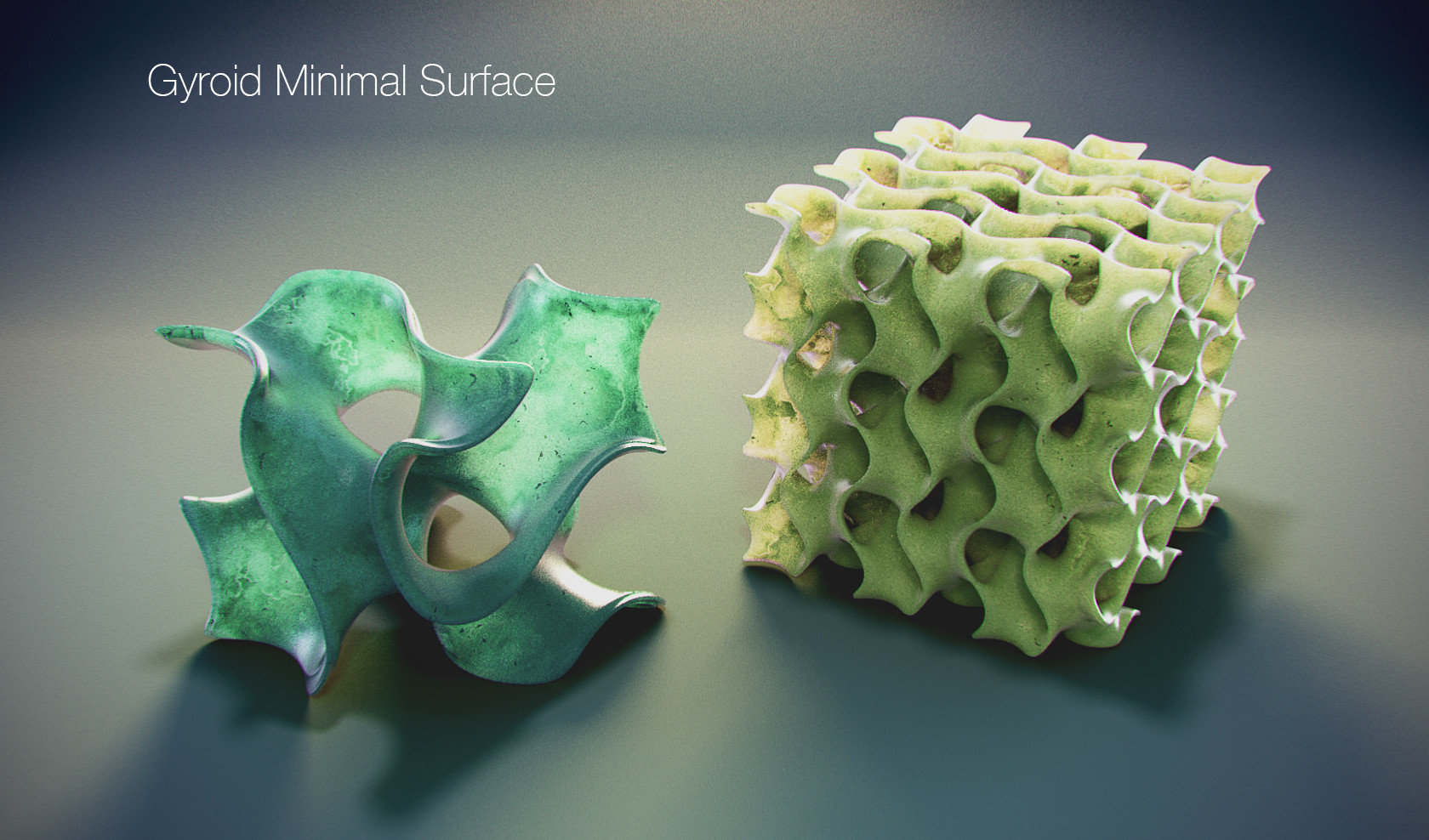

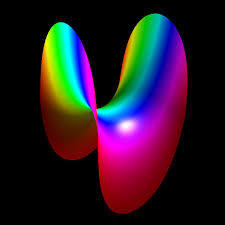
Schwarz P
Heinrich Ferdinand Scherk - 1835
Alan Schoen - 1970
Catenoide
Costa
Helicoide
Enneper

Celso José da Costa - 1982
Leonhard Euler - 1740
Jean Baptiste Meusnier - 1776
Giroide
Alfred Enneper - 1864
Hermann Amandus Schwarz - 1880
Heinrich Ferdinand Scherk erk - 1835
Scherk
- Nas superfícies mínimas as linhas assintóticas estão a 45° em relação as direções principais e, consequentemente, também são ortogonais entre si.
- Nestas direções temos os extremos das torções geodésicas.

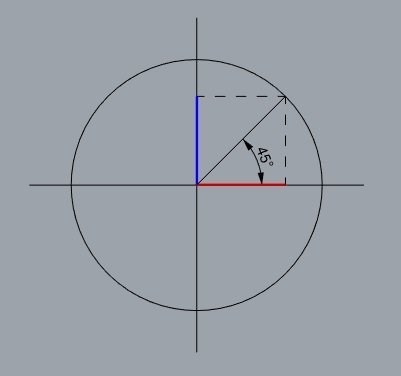
Direções das linhas assintóticas nas superfícies mínimas
k1
k2
assint
Superfícies Mínimas
por busca da forma (form finding)

Schwarz P

Superfície de Enneper vs Parabolóide Hiperbólico (HYPAR)
x = 6 u² v - 2 v³ - 6 v
y = 6 u v² -2 u³ - 6 u
z = -12 u v
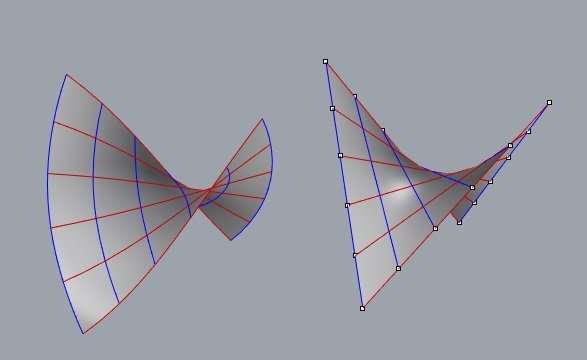

Equação da superfície de Enneper (parametrizada para linhas assintóticas)
Enneper
HYPAR
Enneper
HYPAR
Curiosidade:
As linhas principais de curvatura da Enneper são curvas planas.
Na USP temos dois exemplares do livro "Architectural Geometry" do Prof. Helmut Pottmann (um na FAU outro no IME) no qual você poderá aprender mais sobre o tema, através de belas ilustrações, explicadas em uma linguagem acessível.

Chega de teoria, agora é hora de por a mão na massa...
