Step into the AI Era:
Deep Reinforcement Learning Workshop
(aka how to make AI play Atari games)
Cheuk Ting Ho

@cheukting_ho
Cheukting

Why we like games?
Environment is simple
Actions are limited
Reward is quantified
that is, easy to solve
but Reinforcement Learning is not limited to games
The Journey:
Part 1
- What is Reinforcement Learning
- 101 of Reinforcement Learning
- Crossentropy Method
- Exercise - Crossentropy Method
- Exercise - Deep Crossentropy Method
Part 2
- Model-free Model
- Cliff World: Q-learning vs SARSA
- Exercise - Cliff World
Part 3
- Experience Replay
- Approximate Q-learning and Deep Q-Network
- Exercise - DQN
Agent: cart (Action: left, right)
Environment: the mountain
State: Location of the cart (x, y)
Reward: reaching the flag (+10)
Policy: series of actions
Define the problem
Markov Decision Process
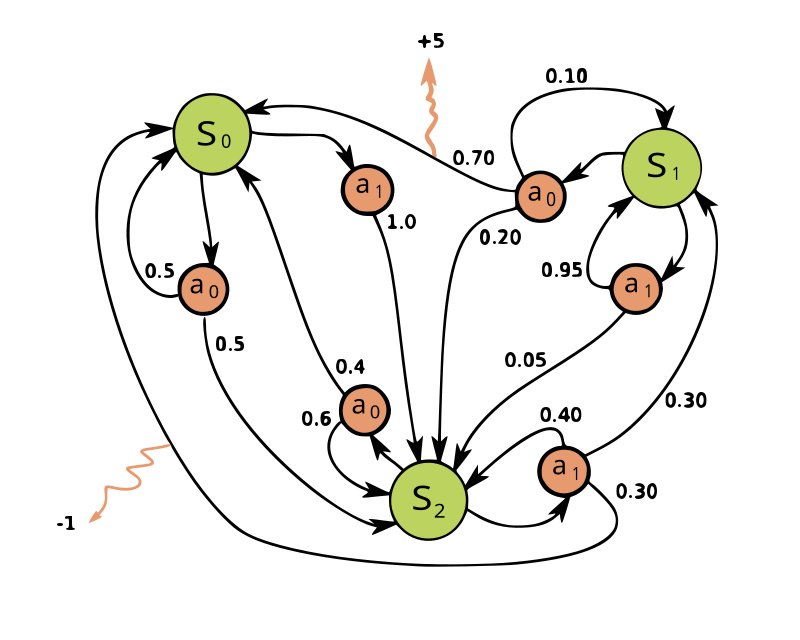
outcomes are partly under the control of a decision maker (choosing an action) partly random (probability to a state)
Cross-entropy method
Tabular
- a table to keep track of the policy
- reward corresponding to the state and action pair
- update policy according to elite state and actions
Deep learning
- approximate with neural net
- when the table becomes too big
*caution: randomness in environment
Cross-entropy method
- Sample rewards
- Check the rewards distribution
- Pick the elite policies (reward > certain percentile)
- Update policy with only the elite policies
Deep learning
- Agent pick actions with prediction from a MLP classifier on the current state
Exercise

Model-free Policy
Bellman equations depends on P(s',r|s,a)
What if we don't know P(s',r|s,a)?
Introduction Qπ(s,a) which is the expected gain at a state and action following policy π
Learning from trajectories
which is a sequence of
– states (s)
– actions (a)
– rewards (r)
Model-free Policy
Model-based: you know P(s'|s,a)
- can apply dynamic programming
- can plan ahead
Model-free: you can sample trajectories
- can try stuff out
- insurance not included
Model-free Policy
Finding expectation by:
1: Monte-Carlo
- Averages Q over sampled paths
- Needs full trajectory to learn
- Less reliant on markov property
2: temporal difference
- Uses recurrent formula for Q
- Learns from partial trajectory
- Works with infinite MDP
- Needs less experience to learn
Exploration vs Exploitation
Don't want agent to stuck with current best action
Balance between using what you learned and trying to find
something even better
Exploration vs Exploitation
ε-greedy
With probability ε take random action;
otherwise, take optimal action
Softmax
Pick action proportional to softmax of shifted
normalized Q-values
Cliff world
(not Doom)
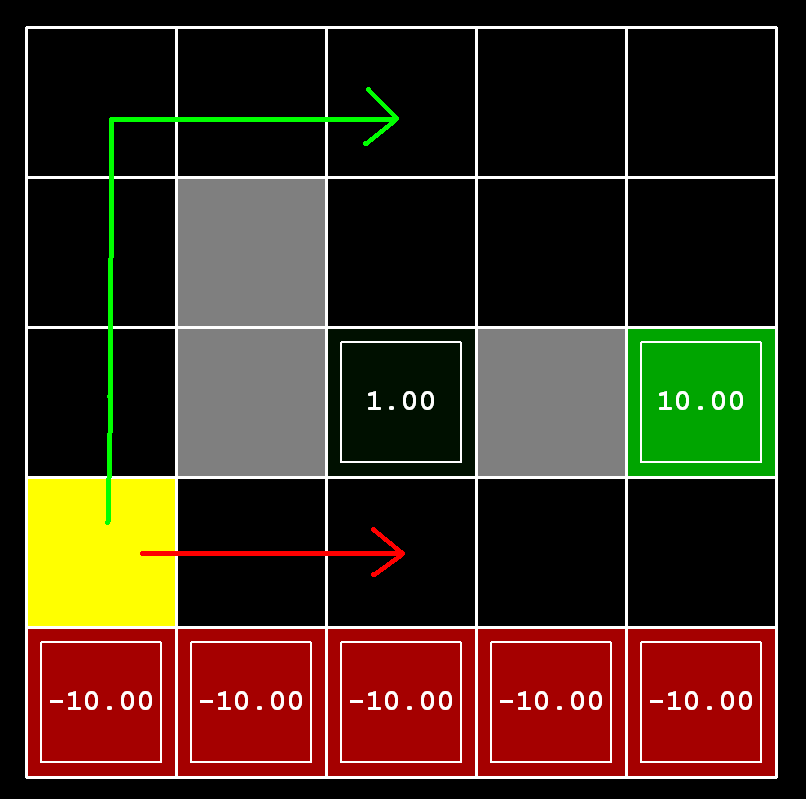
Q-learning will learn to follow the shortest path from the "optimal" policy
Reality: robot will fall due to
epsilon-greedy “exploration"
Introducing SARSA
Cliff world
(not Doom)
Difference:
SARSA gets optimal rewards under current policy
where
Q-learning assume policy would be optimal
Cliff world
(not Doom)
on-policy (e.g. SARSA)
- Agent can pick actions
- Agent always follows his own policy
off-policy (e.g. Q-learning)
- Agent can't pick actions
- Learning with exploration, playing without exploration
- Learning from expert (expert is imperfect)
- Learning from sessions (recorded data)
Exercise

Experience replay
- Store several past interactions in buffer
- Train on random subsamples
- Don't need to re-visit same (s,a) many times to learn it
- Only works with off-policy algorithms
Approx. Q learning
State space is usually large,
sometimes continuous.
And so is action space;
Approximate agent with a function
Learn Q value using neural network
However, states do have a structure,
similar states have similar action outcomes.
DQN
Paper published by Google Deep Mind
to play Atari Breakout in 2015
https://storage.googleapis.com/deepmind-media/dqn/DQNNaturePaper.pdf
Stacked 4 flames together and use a CNN as an agent (see the screen then take action)
DQN
Exercise
