Using Compression Algorithms to Study Physical Systems
Ultimate Goal
Use techniques from information theory to estimate physical properties of biochemical systems
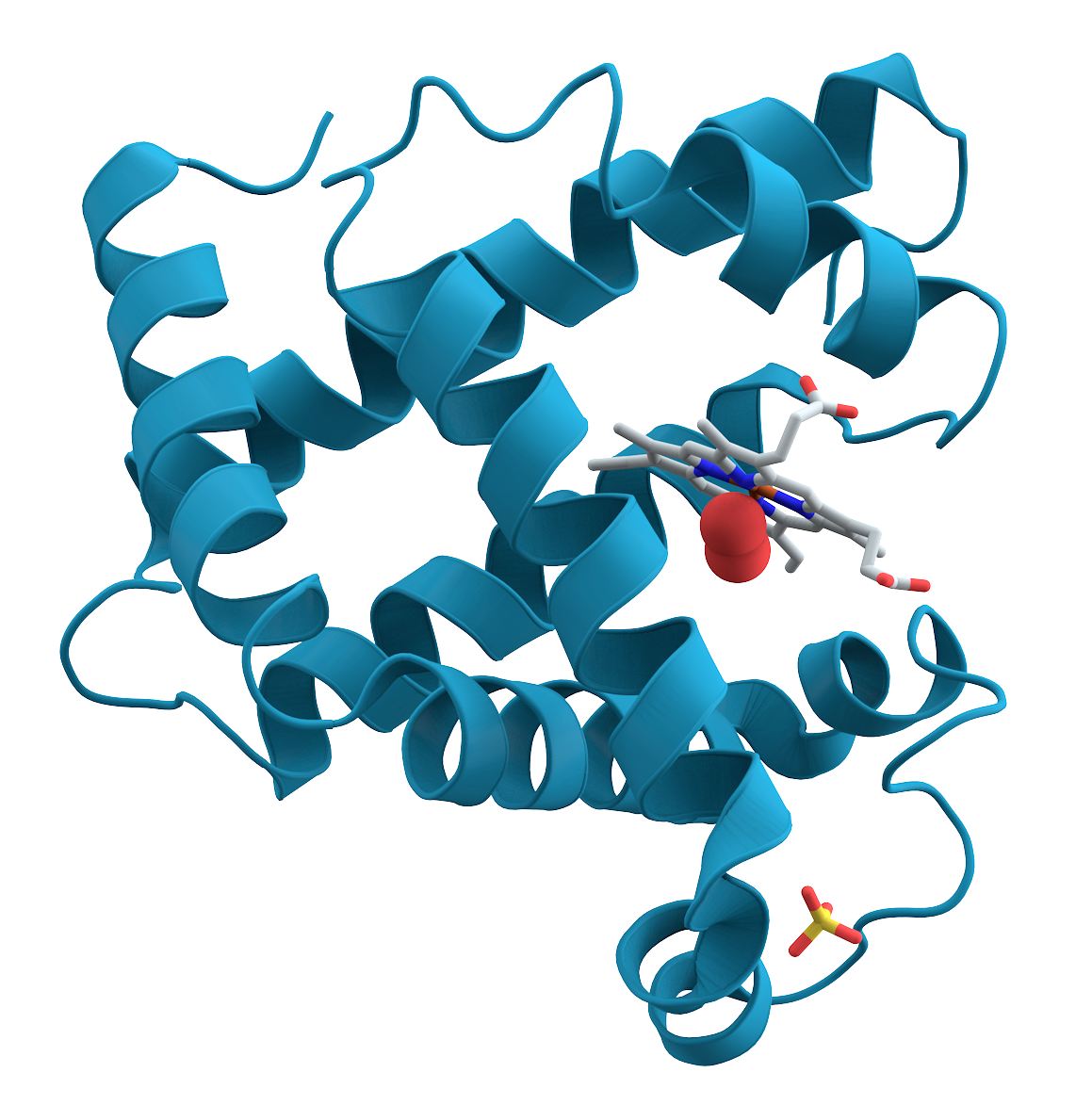
- What is entropy and what does it have to do with physical systems?
- What are existing techniques for estimating entropy?
- How can we improve these techniques?
Outline
Quantifying Randomness
How random are these strings?
110100010110111001101110
000000000000000000000001
We need some sort of context to talk about randomness!
Two major theoretical frameworks to talk about randomness of data:
Shannon Entropy
Kolmogorov Complexity
Shannon, C. E. 1948. “A Mathematical Theory of Communication.” Bell System Technical Journal 27 (4): 623–56.
Shannon Entropy
Shannon entropy describes the randomness of distributions, not samples.
110100010110111001101110
New interpretation: suppose these strings are generated by some random process. What is the entropy (randomness) of that underlying process?
110000100100100101110110
010011011000011000011101
Entropy
"How hard is it to guess the next symbol?"
\(x\) is a string
The Source Coding Theorem
\(N\) i.i.d random variables with entropy \(H(X)\) can be compressed into \(N H(X)\) bits with negligible information loss as \(N \to \infty\), but if they are compressed into fewer than \(N H(X)\) bits, it is virtually certain that information will be lost.
If \(A\) and \(B\) agree on \(X\), how many bits on average must \(A\) send to \(B\) to describe \(N\) observations of \(X\)?
A
B
What does this have to do with physical systems?
What Happens?

Why?
Thermal bath
A: Thermal systems minimize their free energy
Macrostates and Microstates
Define a microstate as a state in which the state of every particle is fully specified.
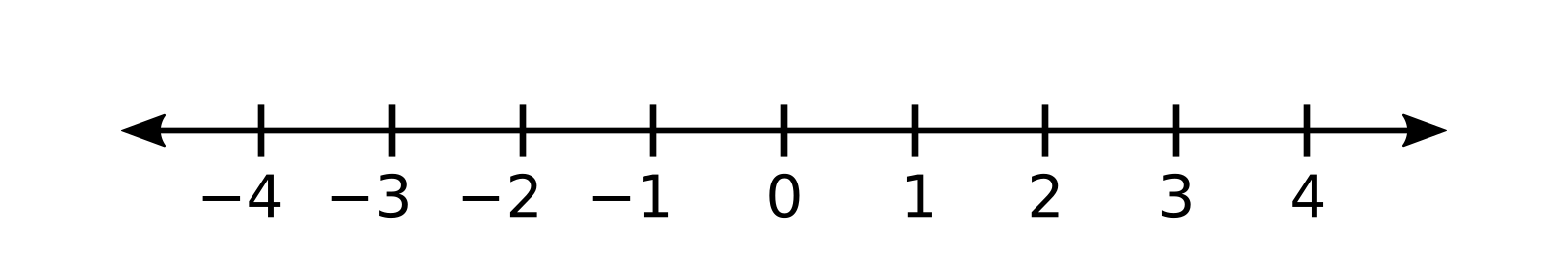
The red particle is at -3, the purple particle is at -1, and the black particle is at 0.
Macrostates and Microstates
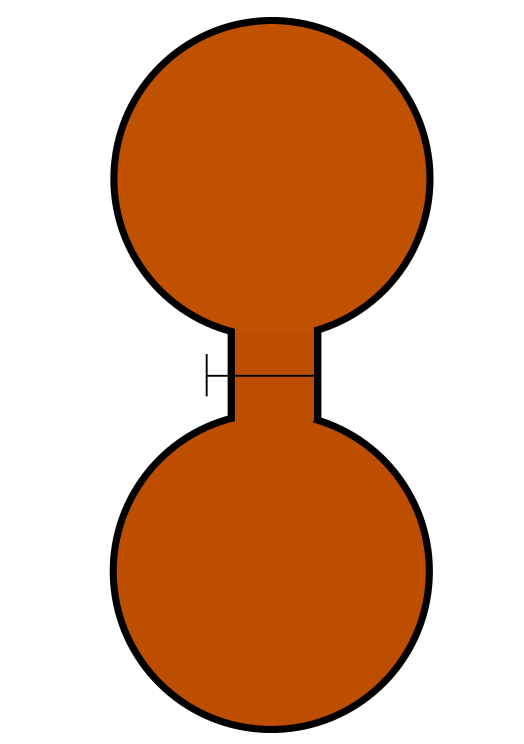
A macrostate is a set of microstates (usually with a simple description).
- All the particles are between -1 and 1
-
The protein is in a folded state
-
The gas occupies half the box
Let \(X\) be some macrostate of a chemical system. Then the entropy of this macrostate is defined as
where
- \(k_B\) is Boltzmann's constant
- \(p(x)\) is the probability of observing microstate \(x\)
Systems minimize their free energy


\(\Delta E > 0\)
\(\Delta S > 0\)
\( sgn(\Delta G)\) depends on \(T\)
Gibbs Entropy:
Shannon Entropy:
You should call it entropy for two reasons: first because that is what the formula is in statistical mechanics but second and more important, as nobody knows what entropy is, whenever you use the term you will always be at an advantage!
—John Von Neumann to Claude Shannon
How important is this effect?
Amprenavir (left) loses a huge amount of entropy when binding to the HIV protease.
It only binds to the HIV protease at all because of even larger gains in entropy/energy elsewhere.
The factors that influence the binding of the drug to its target cannot be fully understood without understanding the entropy of the system.
Chang, Chia-En A., Wei Chen, and Michael K. Gilson. 2007. “Ligand Configurational Entropy and Protein Binding.” Proceedings of the National Academy of Sciences of the United States of America 104 (5): 1534–39.
How important is this effect?
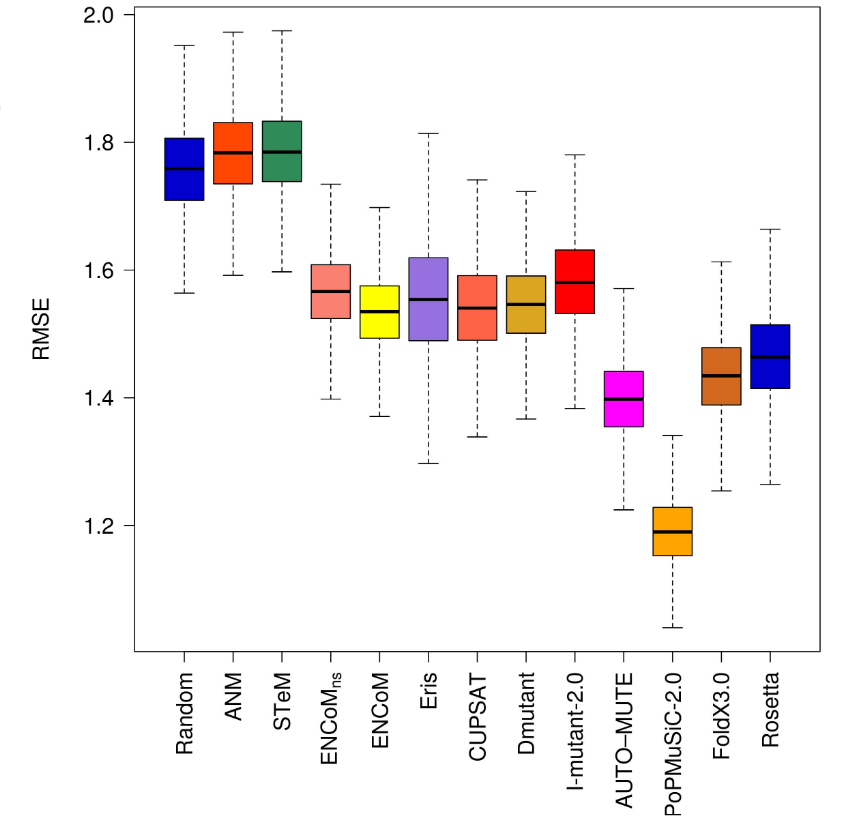
Frappier, Vincent, and Rafael J. Najmanovich. 2014. “A Coarse-Grained Elastic Network Atom Contact Model and Its Use in the Simulation of Protein Dynamics and the Prediction of the Effect of Mutations.” PLoS Computational Biology 10 (4): e1003569.
Error (higher is worse)
How do we estimate entropy?
Entropy Estimators
General
Physical System Specific
Case Study: Self Avoiding Walk

For a walk of length \(N\), there are \( 4 ^ N \) random walks and (approximately) \( 2.638 ^ N \) self-avoiding walks.
For even moderate \( N\), we would need millions of terabytes to store all the possible walks.
From the definition
\(p(x)\) is usually unknown.
Histogram Estimation
| 1 | 2 | 3 | 3 | 4 | 3 | 2 | 3 | 2 | 1 |
|---|
Estimate each the probability of each symbol as the fraction of times it occurs.
There are \(M = 4\) unique outcomes and \(N = 10\) samples. Estimate entropy \(\hat{H}\) as:
Issues with Histogram Estimation
\(\hat{H}\) only works if we assume inputs are independent!
Note on the bias of information estimates. In Information Theory in Psychology: Problems and Methods, pp. 95–100.
The knight rode out on a q
Even if the inputs are i.i.d., the naive entropy estimator is biased, with
In order to get unbiased estimates, we need \(N >> M\).
Block Entropy Estimation
Instead of going symbol-by-symbol, estimate the entropy of an \(n\) block by histogram.
Once upon a midnight dreary
...
on nc ce eu up po on na am mi id
onc nce ceu eup upo pon ona nam
once nceu ceup eupo upon pona
Then take \(\lim\limits_{n \to \infty} H_{n+1} - H_n\) to get entropy
Block Entropy Estimation
Shannon famously used this method to estimate the entropy of the English language in 1951. By using tables of n-grams in the English language (and some clever extrapolation), he was able to derive an estimate of 2.1-2.6 bits per letter.
Shannon, C. E. 1951. “Prediction and Entropy of Printed English.” The Bell System Technical Journal 30 (1): 50–64.
We can now estimate the entropy of systems where symbols are not i.i.d.
Sampling complexity goes up: now need \(N >> M^k\) samples instead of \(N >> M \)
There are many more methods!
- Explicit correction: Miller-Madow
- Markov Chain Construction: CSSR
- Mutual Information Estimators: Grassberger
- Nearest-Neighbor or Density Estimators
Blind Construction of Optimal Nonlinear Recursive Predictors for Discrete Sequences pp. 504--511 in Max Chickering and Joseph Halpern (eds.), _Uncertainty in Artificial Intelligence: Proceedings of the Twentieth Conference_ (2004)
Kraskov, Alexander, Harald Stögbauer, and Peter Grassberger. 2004. “Estimating Mutual Information.” Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 69 (6 Pt 2): 066138.
In all sorts of applications
- Psychological studies
- Neuronal spiking
- Chaotic system studies
- Markov model generation
Note on the bias of information estimates. In Information Theory in Psychology: Problems and Methods, pp. 95–100.
\(N\) i.i.d random variables with entropy \(H(X)\) can be compressed into \(N H(X)\) bits with negligible information loss as \(N \to \infty\), but if they are compressed into fewer than \(N H(X)\) bits, it is virtually certain that information will be lost.

A
B
By Shannon's Source Coding Theorem, this cannot be lower than the true entropy of the distribution.
Several choices of compressor have been proposed:
- LZ77-family methods like GZIP + LZMA
- BWT methods with appropriate sorting routines
- LZ76-family methods: far worse compression, but much better convergence properties.
Cai, Haixiao, S. R. Kulkarni, and S. Verdu. 2004. “Universal Entropy Estimation via Block Sorting.” IEEE Transactions on Information Theory / Professional Technical Group on Information Theory 50 (7): 1551–61.
Physical Entropy Estimators for Biological Systems
Entropy Estimators
General
Physical System Specific
Decomposition-based
Machine Learning
Computational Alchemy
Rapid Overview: Proteins
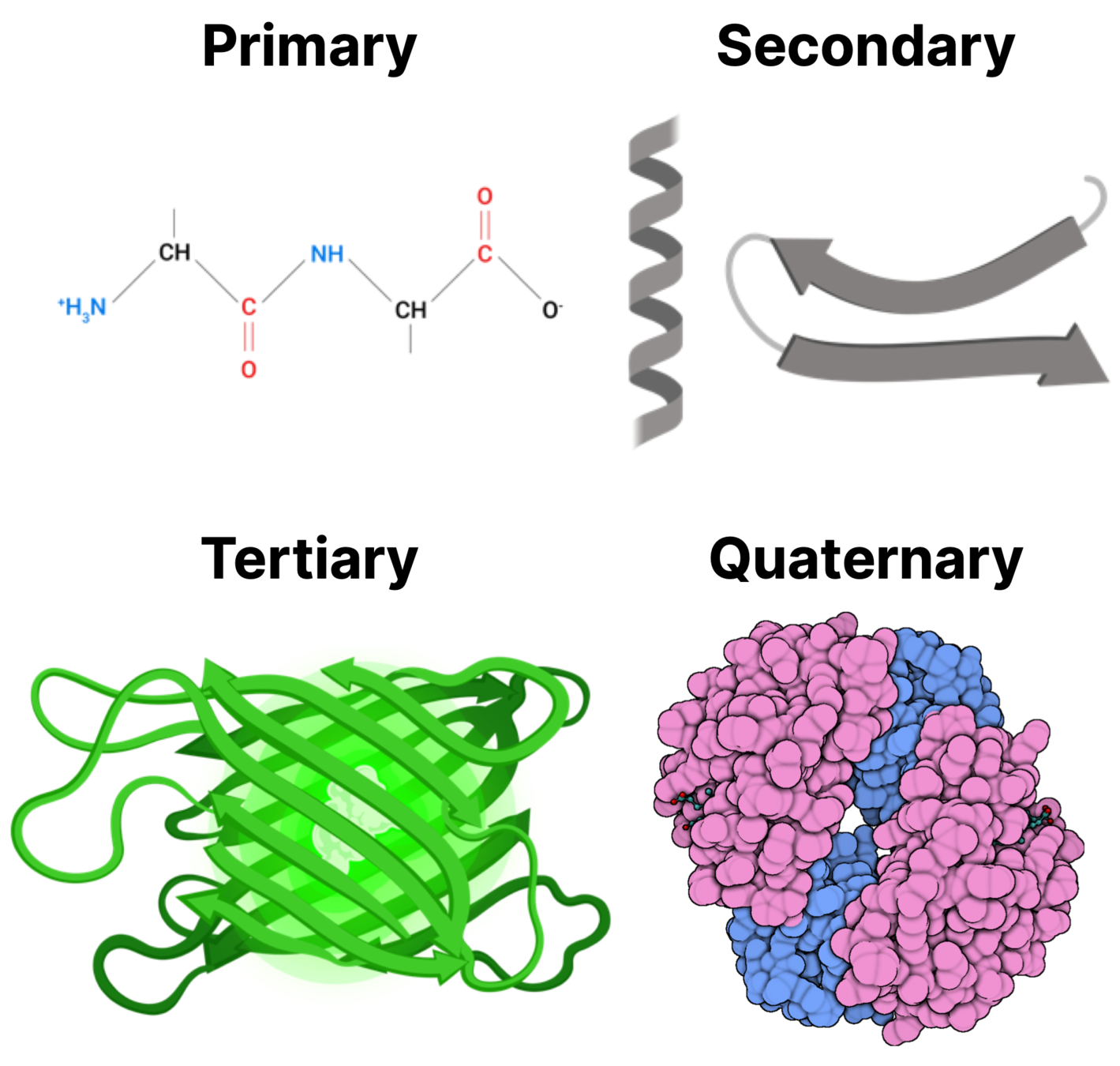
Photo credit: https://walkintheforest.com/Content/Posts/A+Primer+for+Protein+Structure
Attractive/repulsive forces on the atomic level determine how proteins fold:
- Amino acids of opposite charge attract
- Hydrophobic residues want to be buried on the inside of the protein (away from water in the environment)
- Certain amino acids want to form (directional) hydrogen bonds
We understand the basics, but computing useful quantities with them remains frustrating.
R
R
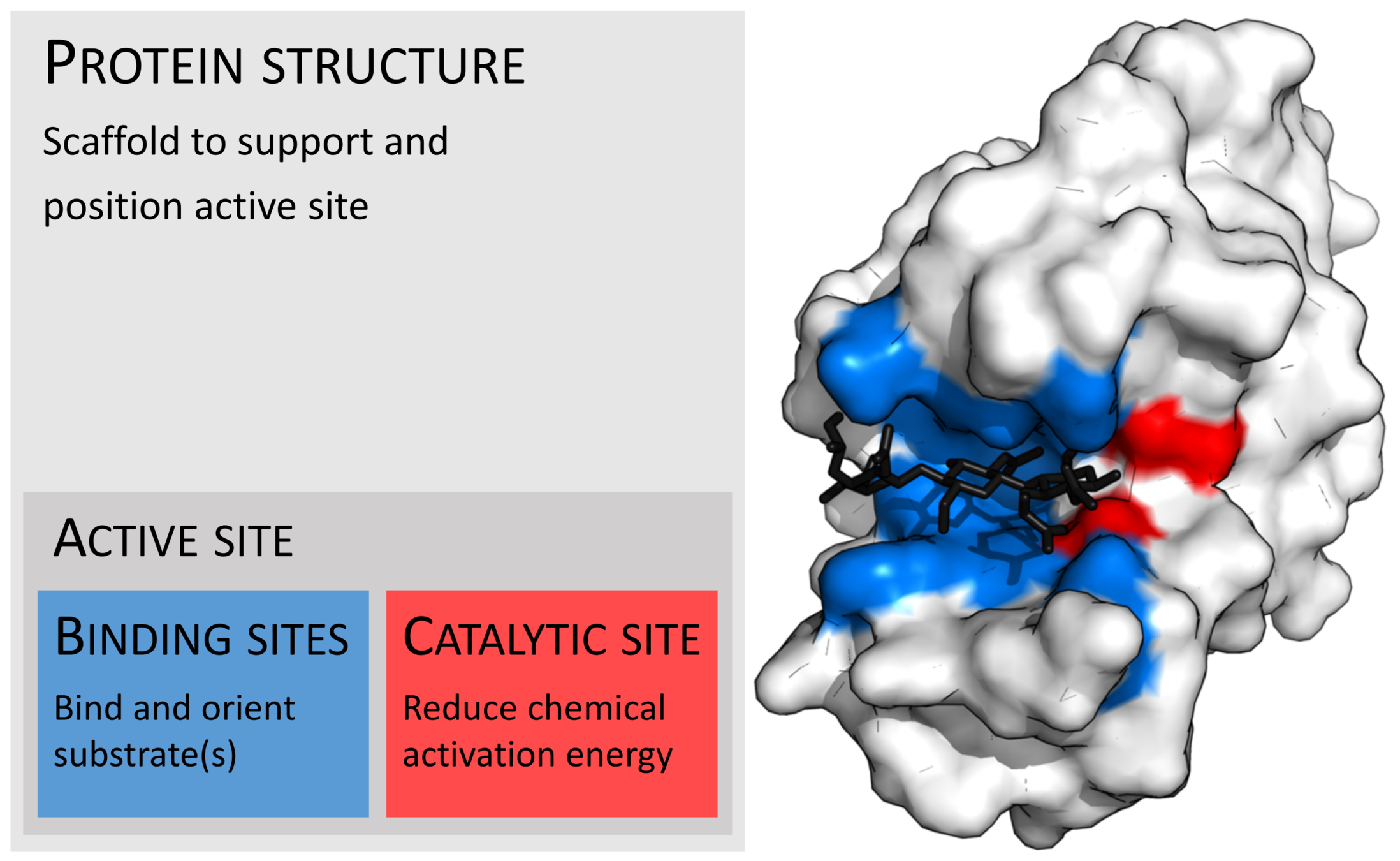
Protein-Ligand
Photo credit: Thomas Shafee - Own work, CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=45801894
Ligands interact with proteins at active sites by the same physical phenomena that control binding.
Similarly to proteins, we understand the basic physical phenomena that control the binding process, but accurately predicting binding is still an open problem.
Probabilities
In the general setting, we did not have a way to compute theoretical probabilities of symbols.
In the setting of physical systems, we (usually) know that the system obeys the Boltzmann distribution:
?
Renormalizing Probabilities
It was proven at STOC in 2000 that this denominator is NP-hard to compute!
Istrail, Sorin. 2000. “Universality of Intractability for the Partition Function of the Ising Model Across Non-Planar Lattices.” 32nd ACM Symposium on the Theory of Computing, 87–96.
This suggests that we can compute explicit probabilities by renormalizing:
Physical Entropy Estimators for Biological Systems
Entropy Estimators
General
Physical System Specific
Decomposition-based
Machine Learning
Computational Alchemy
Quasiharmonic Model
Karplus, Martin, and Joseph N. Kushick. 1981. “Method for Estimating the Configurational Entropy of Macromolecules.” Macromolecules 14 (2): 325–32.
Let's (massively) simplify the problem by assuming that \(E(\vec{x})\) is a quadratic function in \( \vec{x} \).
where \( x_m = \vec{x} - \langle \vec{x} \rangle \)
This is a multivariate Gaussian. We can find the entropy either by integration or by table lookup.
Special Note: EnCOM
The EnCOM model applies a quadratic two-atom, three-atom, and four-atom force for a protein, modulated by the amino acid type of each residue.
Frappier, Vincent, and Rafael J. Najmanovich. 2014. “A Coarse-Grained Elastic Network Atom Contact Model and Its Use in the Simulation of Protein Dynamics and the Prediction of the Effect of Mutations.” PLoS Computational Biology 10 (4): e1003569.



This model is exactly the kind of physics that the Quasiharmonic model was designed to analyze!
Frappier, Vincent, and Rafael J. Najmanovich. 2014. “A Coarse-Grained Elastic Network Atom Contact Model and Its Use in the Simulation of Protein Dynamics and the Prediction of the Effect of Mutations.” PLoS Computational Biology 10 (4): e1003569.

Naive models
QH Entropy ONLY
Machine Learning Models
Physics Models
QH approximation: entire system is one giant quadratic well.
Better approximation: system is composed of several (possibly non-quadratic) wells that the system switches between!
Quasiharmonic
Decomposition: Conformational + Vibrational
Explicit Decomposition
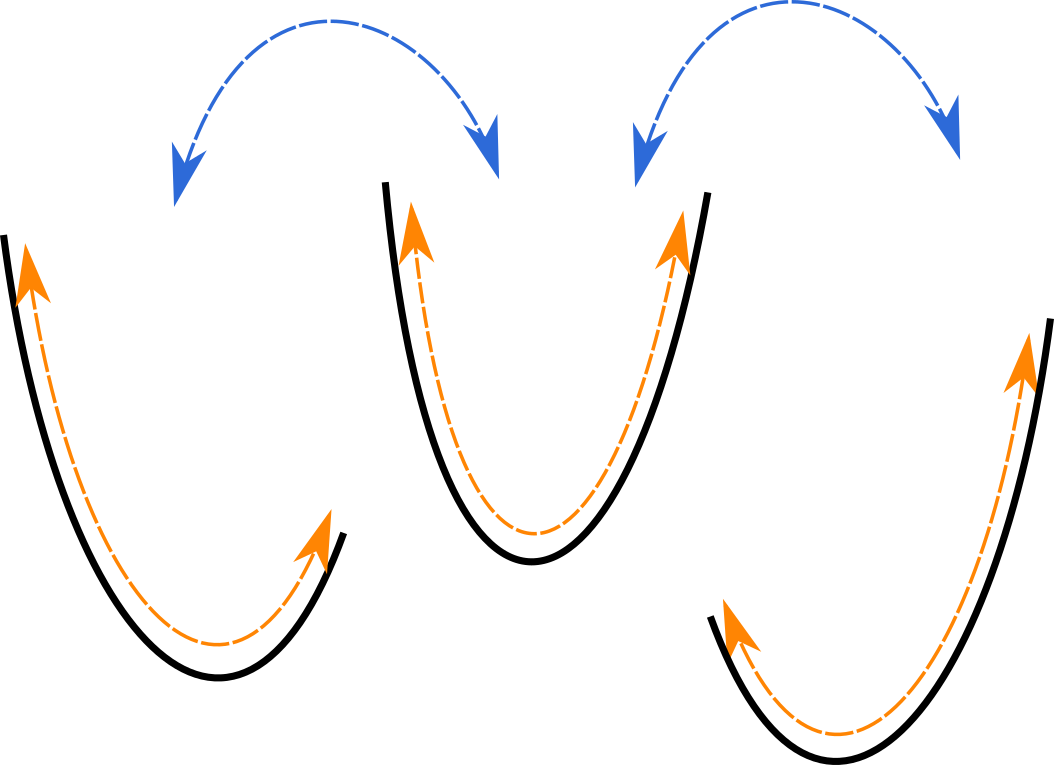
Mining Minima
Find a local minimum
Sample the minimum to find out how wide the well is

Repeat until converged
Head, Martha S., James A. Given, and Michael K. Gilson. 1997. “‘Mining Minima’: Direct Computation of Conformational Free Energy.” The Journal of Physical Chemistry. A 101 (8): 1609–18.
Mining Minima

Chang, Chia-En A., Wei Chen, and Michael K. Gilson. 2007. “Ligand Configurational Entropy and Protein Binding.” Proceedings of the National Academy of Sciences of the United States of America 104 (5): 1534–39.
The protein contribution could be especially important for HIV protease, where binding is associated with a marked reduction in the mobility of the active site flaps...
Used by Chang et. al. in 2007 to obtain the results about Amprenavir discussed earlier
Why don't they do it? Almost certainly it is too costly.
- Amprenavir = 20-30 DoF,
- HIV-1 Protease = 200-300 DoF (in reduced model!)
Decomposition on Timescales
Instead of decomposing spatially, run a simulation and decompose on timescales.
Chong, Song-Ho, and Sihyun Ham. 2015. “Dissecting Protein Configurational Entropy into Conformational and Vibrational Contributions.” The Journal of Physical Chemistry. B 119 (39): 12623–31.
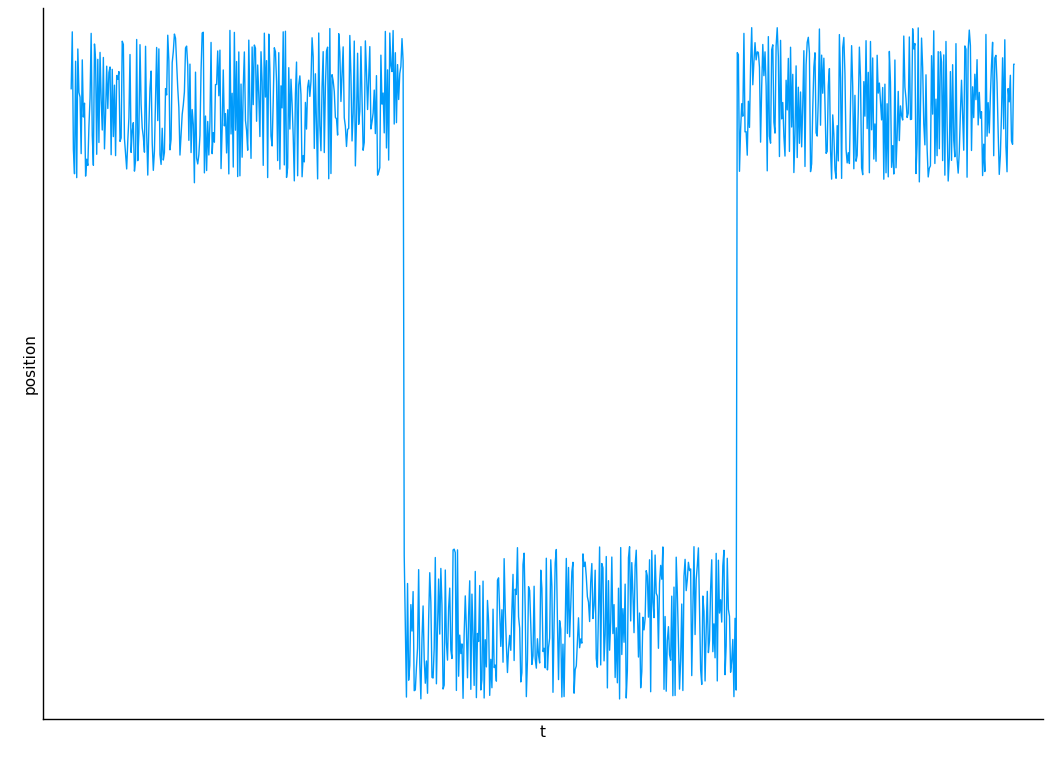
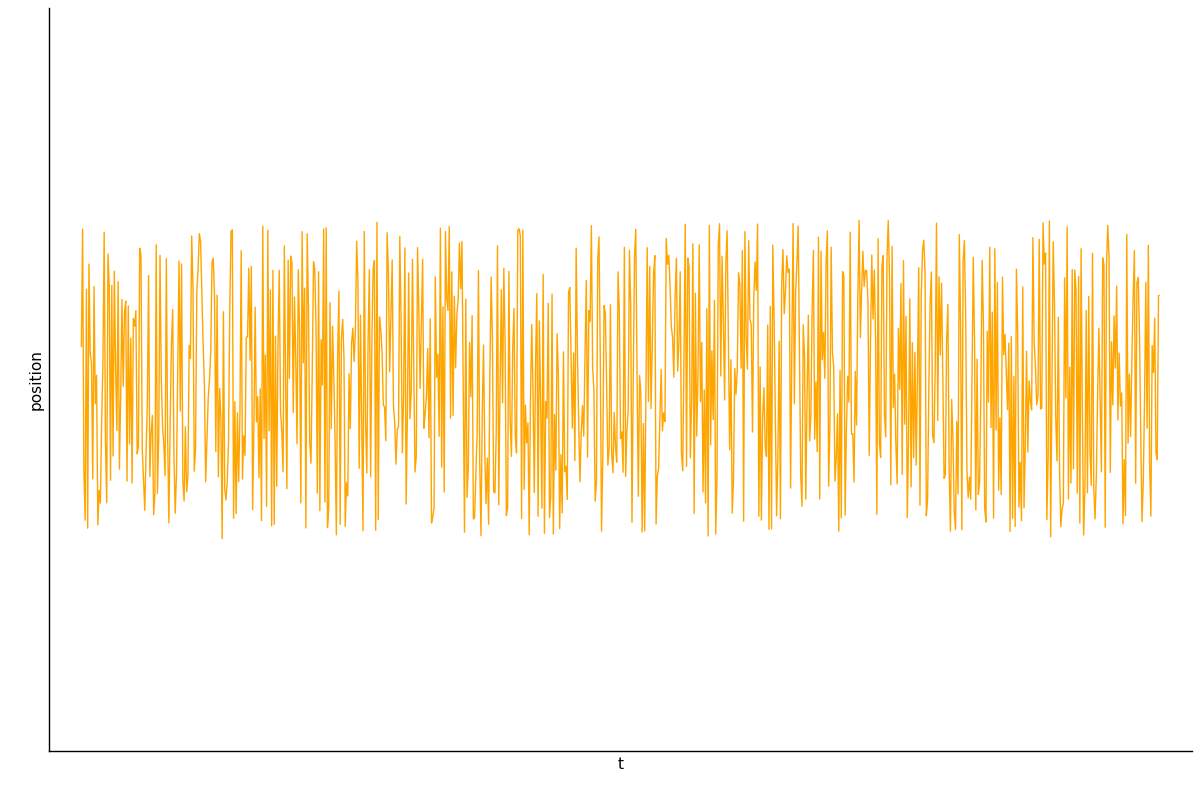
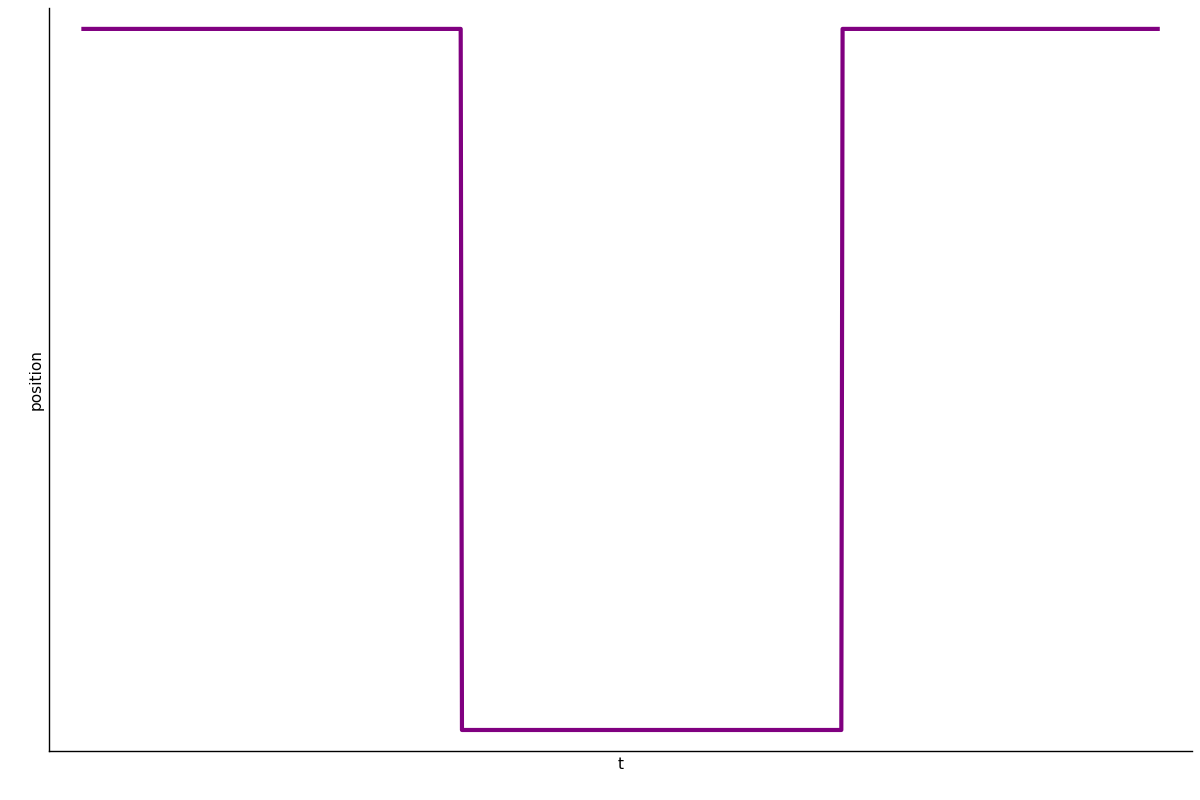
Decomposition on Timescales
Chong, Song-Ho, and Sihyun Ham. 2015. “Dissecting Protein Configurational Entropy into Conformational and Vibrational Contributions.” The Journal of Physical Chemistry. B 119 (39): 12623–31.
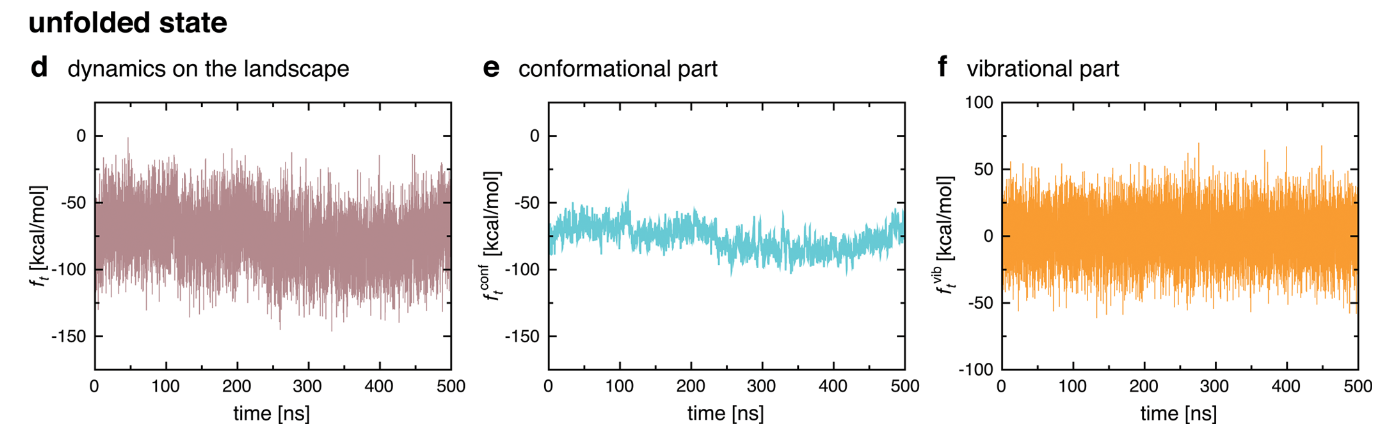
Gives some qualitatively self-consistent results which are interesting, but has not been quantitatively verified.
Physical Entropy Estimators for Biological Systems
Entropy Estimators
General
Physical System Specific
Decomposition-based
Machine Learning
Computational Alchemy
Machine Learning
But there are no ground truth datasets for entropy!
We'll compromise somewhat: instead of trying to learn the entropy directly, we'll try to learn how the stability of the protein changes when you change one of its amino acids.
Image credit: https://en.wikipedia.org/wiki/Protein#/media/File:Myoglobin.png
Classic ML: IMutant
Assumption: stability of the mutant is based primarily on the local environment of the mutation.
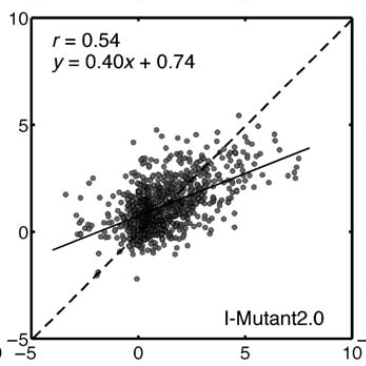
Important!
Unimportant!
Predictors: mutation, native environment, amino acids surrounding mutation. Train with SVM.
Deep Learning?
No known attempts at solving either stability prediction or entropy measurement with deep networks.
There are attempts at using 3D convolutional networks to do mutation work, but these encounter serious issues with training set collection (most high-quality datasets have a few hundred mutations at most)
Normal "Wild Type"
Mutant
Normal "Wild Type"
Mutant
ML: Data Problems
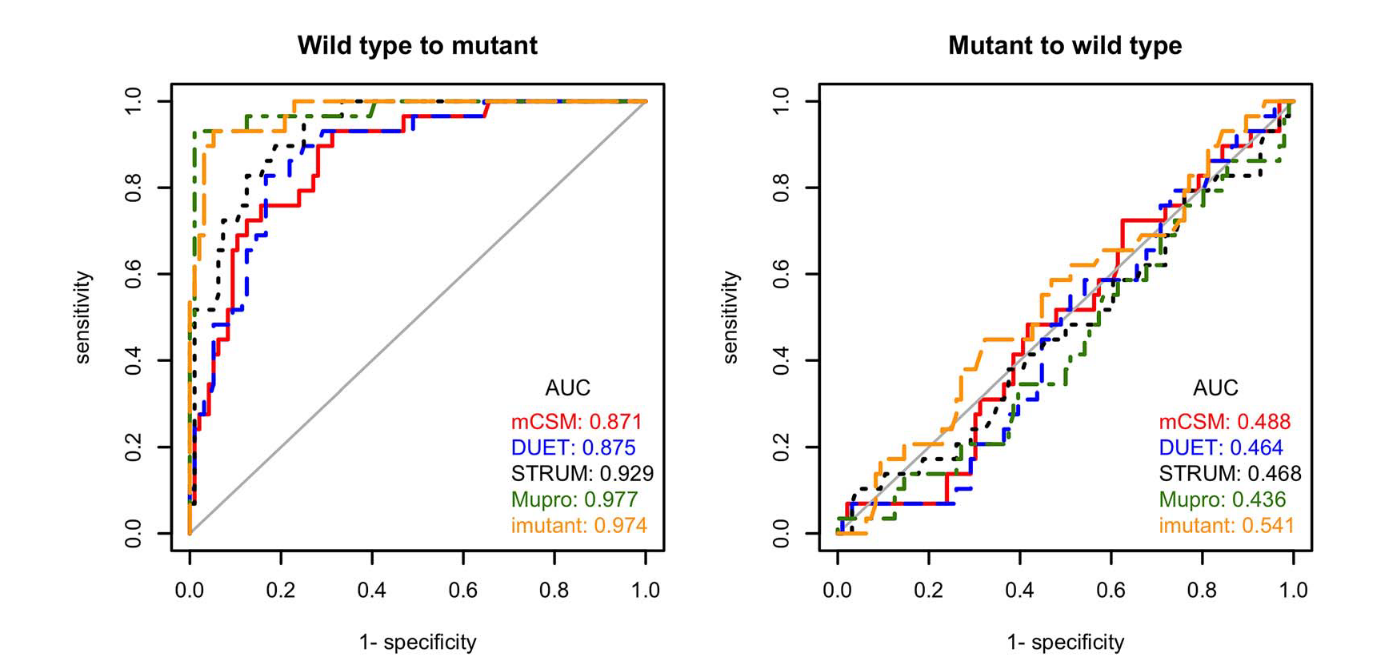
In spite of best efforts to avoid it, almost all machine learning techniques appear to suffer from overfitting.

Fang, Jianwen. 2020. “A Critical Review of Five Machine Learning-Based Algorithms for Predicting Protein Stability Changes upon Mutation.” Briefings in Bioinformatics 21 (4): 1285–92.
Physical Entropy Estimators for Biological Systems
Entropy Estimators
General
Physical System Specific
Decomposition-based
Machine Learning
Computational Alchemy
Computational Alchemy
Free Energy Perturbation (FEP) first proposed by Zwanzig in 1954, but not practical to to do on proteins in silico until 2015 (!) with the invention of improved sampling technique and porting of code onto GPUs.
Zwanzig, Robert W. 1954. “High‐Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases.” The Journal of Chemical Physics 22 (8): 1420–26.
\(f(E_{orange} - E_{blue})\)
\(f(E_{orange} - E_{blue})\)
FEP+: Great Power at Great Cost
Ford, Melissa Coates, and Kerim Babaoglu. 2017. “Examining the Feasibility of Using Free Energy Perturbation (FEP+) in Predicting Protein Stability.” Journal of Chemical Information and Modeling 57 (6): 1276–85.
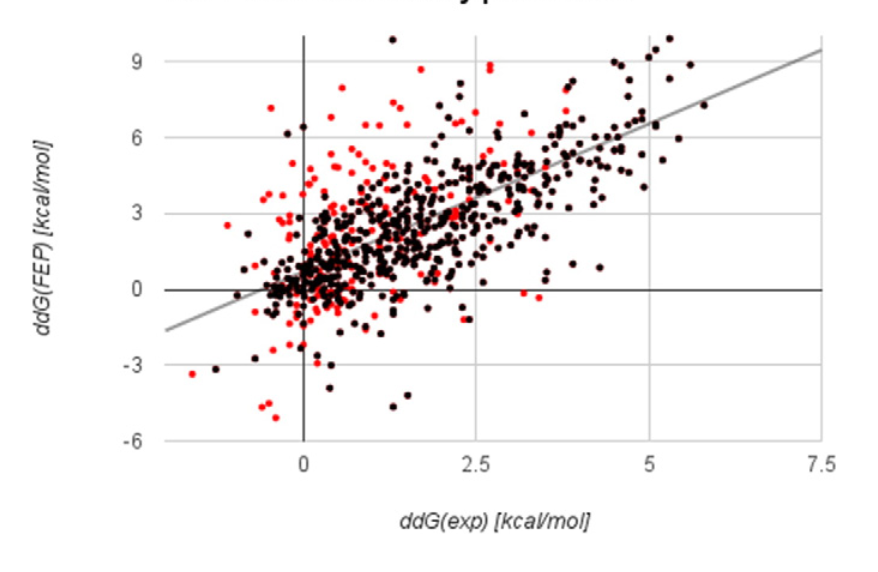
Some of the best mutation-prediction results ever produced!
Time to check 31 mutations with 4 Tesla K80 GPUs:
Steinbrecher, Thomas, Chongkai Zhu, Lingle Wang, Robert Abel, Christopher Negron, David Pearlman, Eric Feyfant, Jianxin Duan, and Woody Sherman. 2017. “Predicting the Effect of Amino Acid Single-Point Mutations on Protein Stability-Large-Scale Validation of MD-Based Relative Free Energy Calculations.” Journal of Molecular Biology 429 (7): 948–63.

Potapov, Vladimir, Mati Cohen, and Gideon Schreiber. 2009. “Assessing Computational Methods for Predicting Protein Stability upon Mutation: Good on Average but Not in the Details.” Protein Engineering, Design & Selection: PEDS 22 (9): 553–60.
180 hours (7.5 days)
In addition, without specialized software + support, almost impossible for non-experts to run.
Quasiharmonic Approximation
Mining Minima Decomposition
Temporal Decomposition
Machine Learning
FEP (Alchemy)
- Fast, simple, performs decently
- Fails when energy landscape really does consist of multiple minima (e.g. for unfolded proteins, intrinsically disordered proteins)
- Performs decently well for small molecules
- Very slow (impossible?) to use on proteins
- Acceptable performance
- Deep learning is still very young, suffers from lack of training data
- Currently gold standard for performance
- Also a gold standard for price (not in a good way)
- Performance (in time) is perfectly fine!
- Not quantitatively verified
Physical Entropy Estimators for Biological Systems
Entropy Estimators
General
Physical System Specific
Decomposition-based
Machine Learning
Computational Alchemy
Information Theoretic
Compression
In 2019, two simultaneous papers (Avinery et. al and Martiniani et. al.) suggested a mechanism for using compression to estimate the entropy of physical systems.
Avinery, Ram, Micha Kornreich, and Roy Beck. 2019. “Universal and Accessible Entropy Estimation Using a Compression Algorithm.” Physical Review Letters 123 (17): 178102.
Martiniani, Stefano, Paul M. Chaikin, and Dov Levine. 2019. “Quantifying Hidden Order out of Equilibrium.” Physical Review X 9 (1): 011031.
A
B
- Simulate
- Coarse-grain
- Compress
Protein Trace
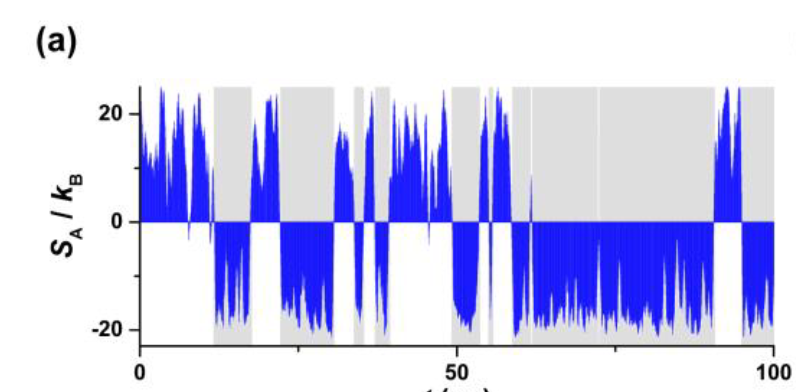
Lindorff-Larsen, Kresten, Stefano Piana, Ron O. Dror, and David E. Shaw. 2011. “How Fast-Folding Proteins Fold.” Science 334 (6055): 517–20.
Quasiharmonic Approximation
Mining Minima Decomposition
Temporal Decomposition
Machine Learning
FEP (Alchemy)
- Fast, simple, performs decently
- Fails when energy landscape really does consist of multiple minima (e.g. for unfolded proteins, intrinsically disordered proteins)
- Performs decently well for small molecules
- Very slow (impossible?) to use on proteins
- Acceptable performance
- Deep learning is still very young, suffers from lack of training data
- Currently gold standard for performance
- Also a gold standard for price (not in a good way)
- Performance (in time) is perfectly fine!
- Unclear whether the approach is quantitatively correct.
Compression
?
Exploring the Compression Method
The LZMA compressor uses a lookback algorithm to compress.
hellohellohello
hello<5,5><10,5>
Lookback is often inhibited in the presence of floating-point numbers:
3.14129,3.14126,3.14127
To solve this, Avinery et. al. choose to coarse-grain their trace to get rid of the least significant bits (numerical noise).
3.17828
3.07845
2.83242
2.59205
2.39350
2.06782
1.95222
3
3
2
2
2
2
1
How to choose bin size? Try a bunch of bins and see what gets you the lowest compression ratio (subject to a cutoff which is eyeballed from plots).
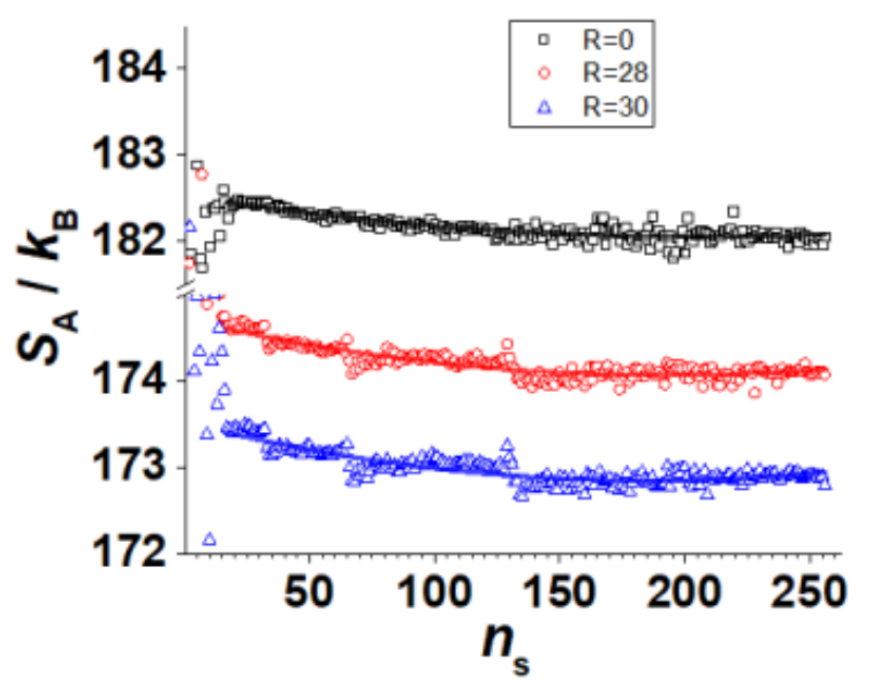
Avinery's Results
Avinery et. al. demonstrated quantitatively correct results for several model systems, including an Ising model (traditionally hard for the same reason as the self-avoiding walk).
Martiniani et. al. demonstrate qualitatively correct results for several other toy systems.
Is this technique quantitatively useful? Can we produce accurate numbers?
What conditions do we need for high quality results?
Attempted Application: Ring Closing
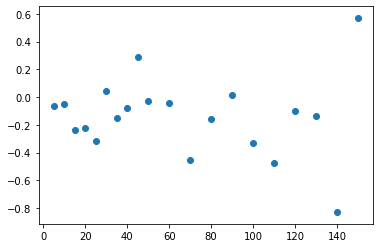
Expected Result
Actual Result
Attempted Application: Folding Rate
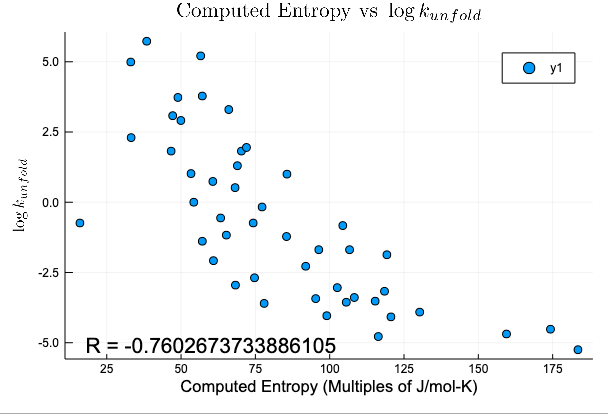
Compression Method
Protein Size
(2 removed outliers)
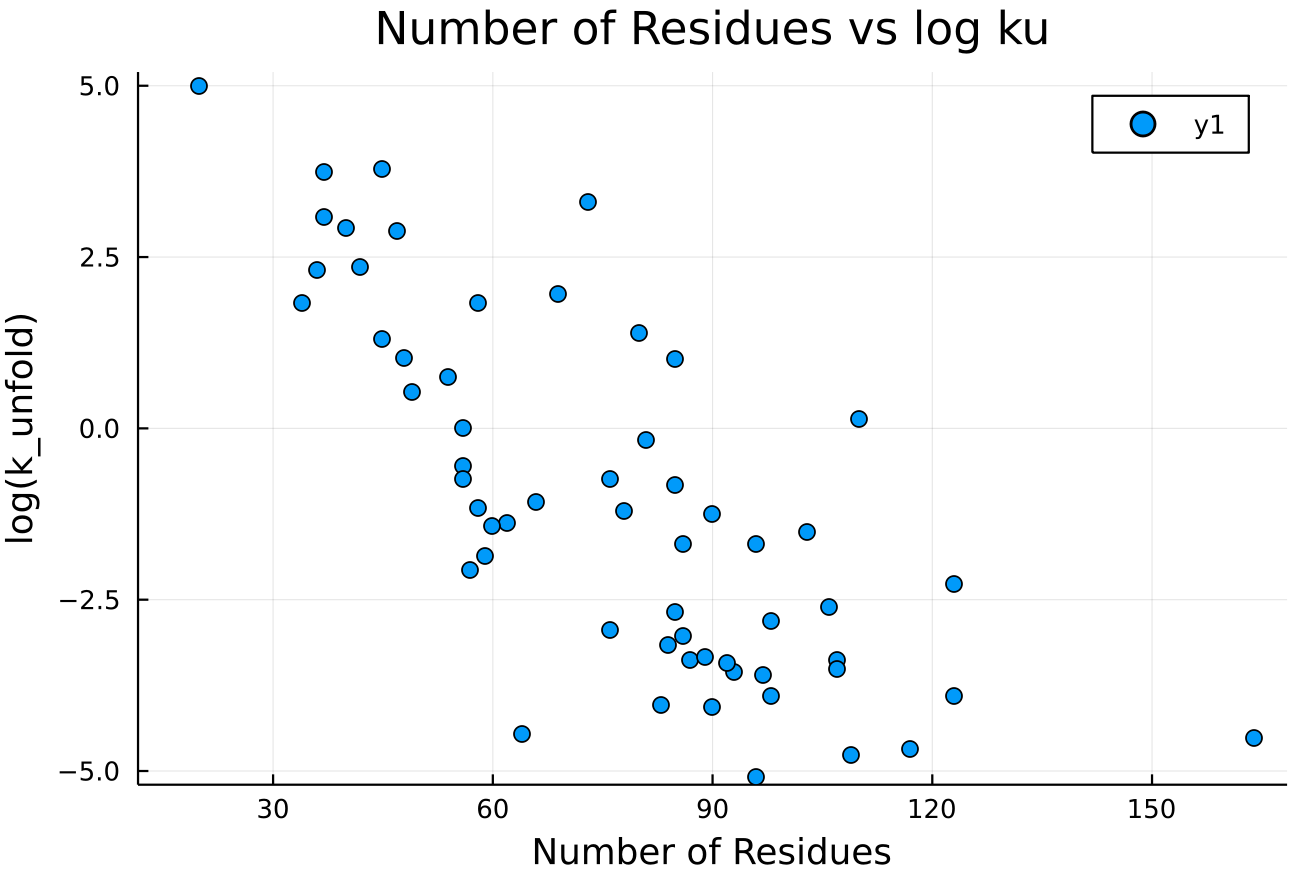
R = -0.8177644223347599
What is going wrong?
And can we fix or avoid it?
Not Enough Samples
The compressor does not necessarily require dense samples, but it does require some minimum amount (e.g. with a single sample, clearly compressor will fail).
This interacts with the choice of number of bins per dimension: the more bins per dimension, the more samples we need to make sure that the appropriate bins are sampled.


Not Enough Samples
Solution: Determine minimum bounds for sampling. Given \(M\) bins per dimension in \(d\) dimensions, we can write bounds for how many samples we need to guarantee that each bin is sampled \(k\) times w.h.p.
Schürmann, Thomas. 2002. “Scaling Behaviour of Entropy Estimates.” Journal of Physics A: Mathematical and General 35 (7): 1589–96.
Would definitely like looser bounds based on compressor convergence, e.g. from Schürman 2002
Suppose we have \(M^d\) bins and want to sample each bin at least \(k\) times with probability at least \(1 - \delta\). To do this, we need to take \(n\) samples, with \(n\) satisfying
Not Enough Bins
Given a fixed number of bins, we know how many samples we need to guarantee that we're in a well-sampled regime.
But if the binsize is too large, we cannot capture small scale changes in the probability function.
Not Enough Bins
To determine if this issue is present, we have derived bounds on the estimated probability in terms of the change in the probability density function across the bin. In particular:
Unpublished
Let \(p(x)\) be the probability density function on a bin and \(\tilde{p}(x)\) be the mean of \(p(x)\) over that bin. If \(\left| \frac{p(x) - \tilde{p}(x)}{p(x)} \right| < \epsilon_p\) across all bins, then
And a similar expression bounds \(H(p)\) from below.
*N.B.: This bound isn't quite correct: the true bound relies on some mathematical formalism I don't have time to introduce

\(p(x)\)
\(\tilde{p}(x)\)
Bad Representation
Consider a 2D Ideal chain. What is the best way to represent it?
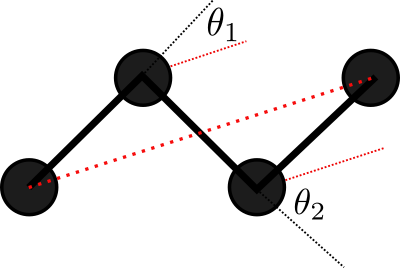

Experiments show that the representation on the right is better for the compressor. Why?
We have evidence showing that smaller variances in values helps the compressor, but as of yet, no unified (principled) way of picking a representation that is amenable to compression.
In Summary
Compressor-based method:
- Known to get good quantitative results on toy systems
- Can get qualitatively interesting results on real proteins
- Can get quantitatively good results for some protein problems (new!)
- Struggles to get quantitatively good results for some protein problems (new!)
- Is dependent on representation used for the system, with different representations giving different results (new!)
Future Goals
- Establish better rules for determining bin and sample counts based on information about problem (distribution of input, desired accuracy, etc).
- Determine rules for picking an appropriate representation of system (or at least, how to determine if we are in a bad representation).
- (If necessary) Try other information-theoretic techniques to see if they align better with the kinds of data available in physics
FIN
Questions?
Appendix
Kolmogorov Complexity
The length of the shortest program needed to generate the string on a Universal Turing Machine
def generate(out,n):
for i in range(1,n):
out += "0" + "1" * i0101101110111101111101111110...
def generate(out,n):
out = "110100010110111001101110"110100010110111001101110...
Chaitlin's Theorem
Most strings are Kolmogorov-random!
Can we demonstrate this?
Chaitlin's Incompleteness Theorem tells us that for a given UTM, there is a constant \(L\) such that we cannot prove that the Kolmogorov-complexity is larger than \(L\).
Most strings are Kolmogorov-random, but we cannot prove this!
Discrete and Differential Entropy
Discrete Entropy
Differential Entropy
These two quantities are not equivalent, not even in a limiting sense!
The discrete KL Divergence onto a uniform reference distribution can also unify these quantities.
FEP Details
Based on the free energy difference equation proposed by Zwanzig in 1954
Problem: regions where \(E(B) - E(A)\) is large might be rarely sampled under \(A\)--leads to very slow convergence.
FEP Details
Solution: alchemy! Define a new energy function:
This is "not computational chemistry" because the state we're simulating (blend of two real states) is not real itself. We're simulating an alchemical state.
Step \( \lambda \) from 0 to 1 in small increments, applying Zwanzig's equation at each step, to get a chain of free energy differences.
How is this CS?
Questions of convergence and sample complexity
Opportunities to develop more efficient algorithms for estimating information-theoretic quantities in a specific domain.
Definitely straddling a boundary between computational and computer science.