Codechef Cook off
JUNE 2020
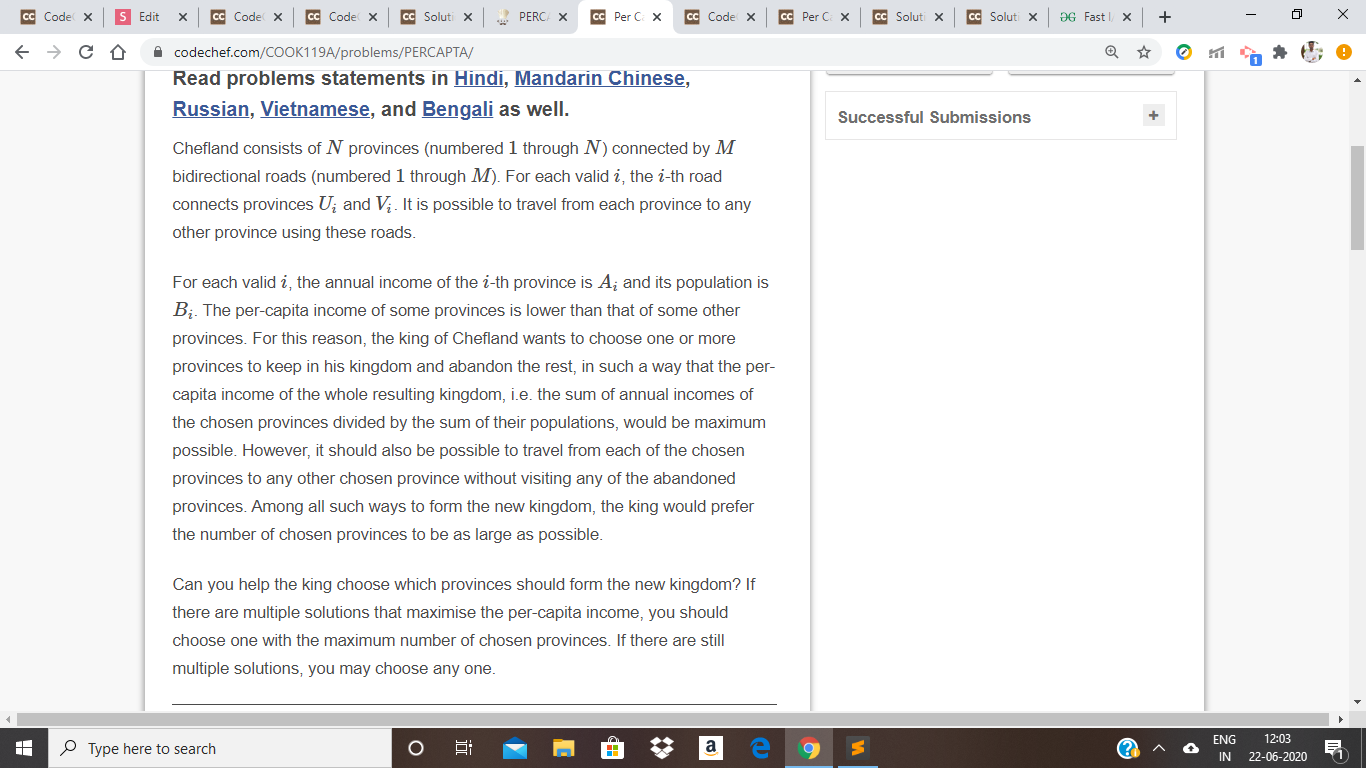
PROBLEM - Per Capita Income (PERCAPTA)
PROBLEM DESCRIPTION
Observations from the problem..!!
Since chef want to select the provinces such that its per capita income is maximized..!!
Observations from the problem..!!
Since chef want to select the provinces such that its per capita income is maximized..!!
Also chef wants to select maximum provinces..!!
TASK - 1
What will be the criteria of selection of provinces?
TASK - 1
What will be the criteria of selection of provinces?
Let us take some examples to understand this..!!
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
TASK - 1
What will be the criteria of selection of provinces?
Let us take some examples to understand this..!!
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
Per capita income
| 3 | 2 | 2 | 3 |
|---|
TASK - 1
What will be the criteria of selection of provinces?
Let us take some examples to understand this..!!
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
Per capita income
| 3 | 2 | 2 | 3 |
|---|
TASK - 1
What will be the criteria of selection of provinces?
Let us take some examples to understand this..!!
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
Per capita income
| 3 | 2 | 2 | 3 |
|---|
27/11 = 2.45
TASK - 1
What will be the criteria of selection of provinces?
Let us take some examples to understand this..!!
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
Per capita income
| 3 | 2 | 2 | 3 |
|---|
2.45
TASK - 1
What will be the criteria of selection of provinces?
Let us take some examples to understand this..!!
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
Per capita income
| 3 | 2 | 2 | 3 |
|---|
30/15 = 2
TASK - 1
What will be the criteria of selection of provinces?
Let us take some examples to understand this..!!
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
Per capita income
| 3 | 2 | 2 | 3 |
|---|
66/25 = 2.64
TASK - 1
What will be the criteria of selection of provinces?
Let us take some examples to understand this..!!
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
Per capita income
| 3 | 2 | 2 | 3 |
|---|
That means if we take average of per capita income of different provinces it will always be less than maximum per capita income in that subset.
Approach
So now what we could think off from the obeservations is we will get maximum per capita income for different provinces when we take province of maximum per capita income from others..!!
Approach
So now what we could think off from the obeservations is we will get maximum per capita income for different provinces when we take province of maximum per capita income from others..!!
But also we want maximum number of provinces..!!
Approach
So now what we could think off from the obeservations is we will get maximum per capita income for different provinces when we take province of maximum per capita income from others..!!
But also we want maximum number of provinces..!!
It is simple we will select all the provinces which have per capita income as maximum per capita income
Approach
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
Per capita income
| 3 | 2 | 2 | 3 |
|---|
Approach
Income
Population
| 15 | 12 | 18 | 48 |
|---|---|---|---|
| 5 | 6 | 9 | 16 |
Per capita income
| 3 | 2 | 2 | 3 |
|---|
Per capita income = (15 + 48) / (16 + 5) = 63/21 = 3
Approach
Summarizing the approach
1. Calculate per capita income of all provinces (take long double).
Approach
Summarizing the approach
1. Calculate per capita income of all provinces (take long double).
2. Find the maximum per capita income and find all the provinces which has same maximum per capita income..!!
3. Now to check what is the maximum number of provinces amongst these which are connected apply dfs to these provinces..!!
If you want to know about what is DFS(Depth first search) in graphs and other algorithms of graphs
If you want to know about what is DFS(Depth first search) in graphs and other algorithms of graphs
Check out my playlist of graphs for competitive programming..!!
If you want to know about what is DFS(Depth first search) in graphs and other algorithms of graphs
Check out my playlist of graphs for competitive programming..!!
Link in the description..!!
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while(t--)
{
int n,m;
cin >> n >> m;
long double population[n];
long double income[n];
int mark[n] = {0};
for(int i =0; i<n; i++)
cin >> income[i];
for(int i =0; i<n; i++)
cin >> population[i];
long double max_inc = 0;
for(int i =0; i<n; i++)
{
long double t;
t = income[i]/population[i];
if(t > max_inc)
max_inc = t;
}
std::vector<int> max_inc_nodes;
for(int i =0; i<n; i++)
{
if(income[i]/population[i] == max_inc)
{
mark[i] = 1;
max_inc_nodes.push_back(i);
}
}
std::vector<int> final;
int visited[n] = {0};
for(int i = 0; i<max_inc_nodes.size(); i++)
{
vector<int> temp;
temp.push_back(max_inc_nodes[i]);
if(visited[max_inc_nodes[i]] == 0)
dfs(edges,max_inc_nodes[i],mark,temp,visited);
if(temp.size() > final.size())
{
final = temp;
}
temp.clear();
}
cout << final.size() << endl;
for(int i =0; i<final.size(); i++)
cout << final[i]+1 << " ";
}
return 0;
}void dfs(vector<int>* edges, int sv, int mark[], vector<int>& temp, int visited[])
{
visited[sv] = 1;
for(int i = 0; i<edges[sv].size(); i++)
{
if(visited[edges[sv][i]] == 0 && mark[edges[sv][i]] == 1)
{
temp.push_back(edges[sv][i]);
dfs(edges,edges[sv][i],mark,temp,visited);
}
}
}Standard DFS code
Still, Have any Doubts???
Still, Have any Doubts???
Comment it You will get a reply
OR
Send your doubt to email provided in description.