Tensors are multilinear maps

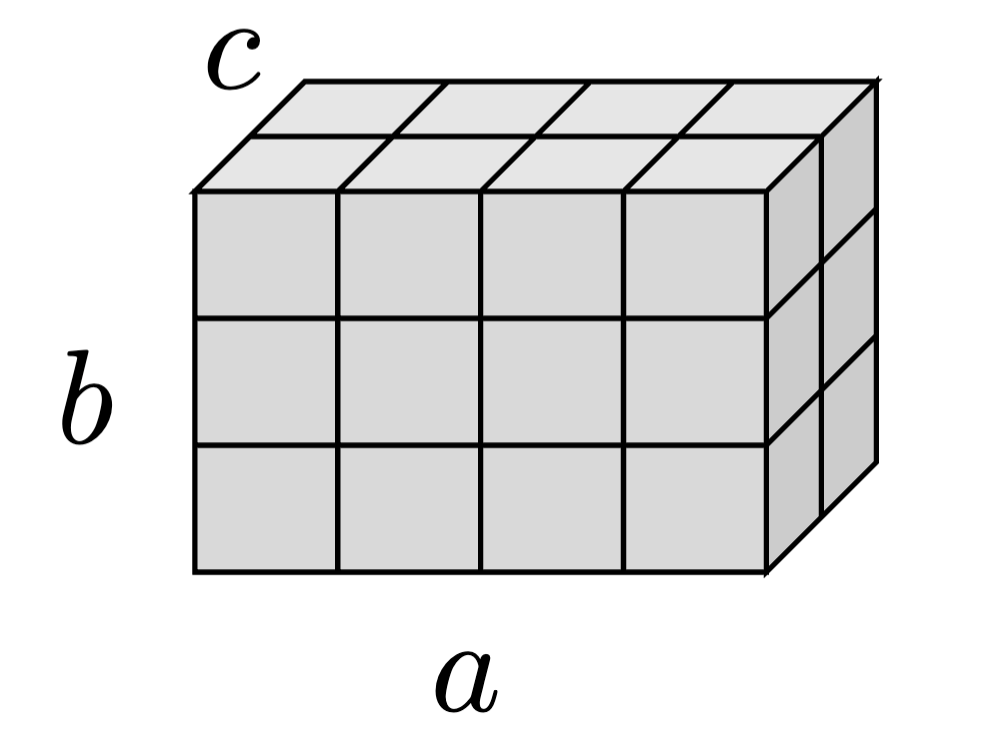
\( T \) is \( (a \times b \times c) \) grid of numbers

Example 1: Multiplication 

Let \( A \) be a K-vector space with bilinear multiplication \( \mu: A \times A \rightarrowtail A \) (a \(K\)-algebra)

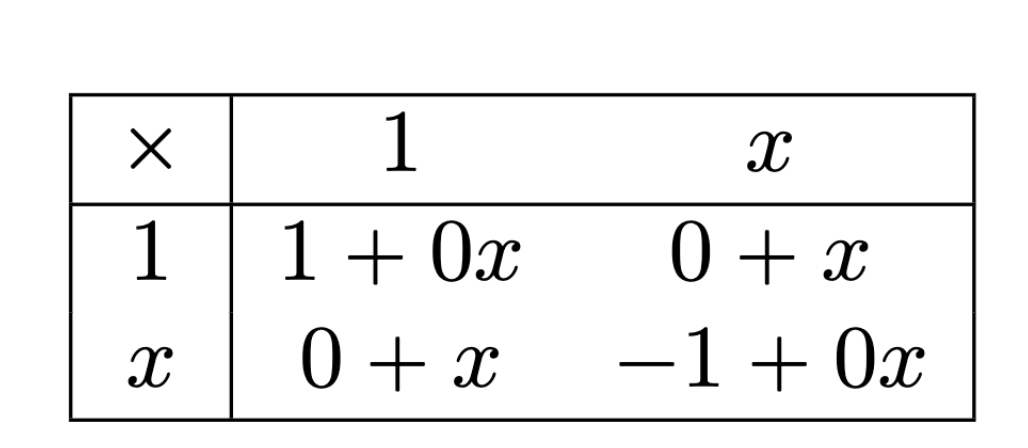
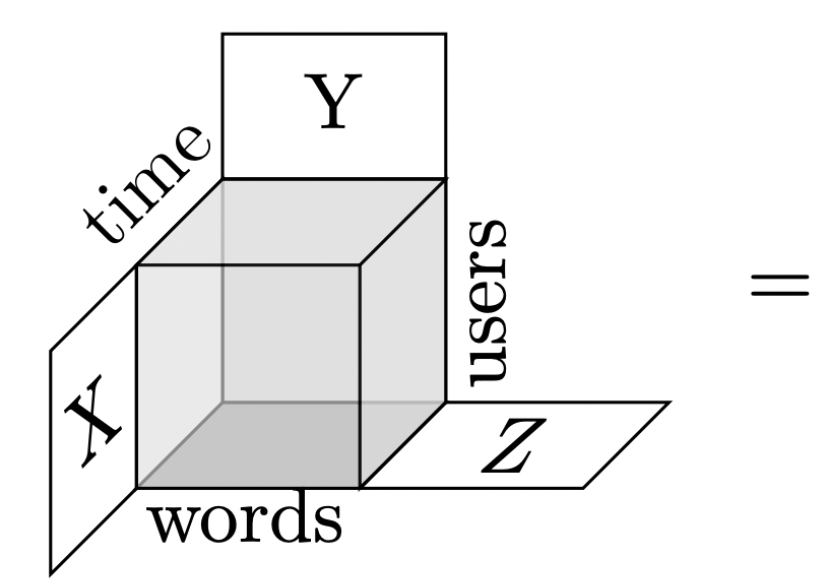
Example 2: Discord chat logs

\(\text{Users}\) = \( \mathbb{R}^{\{\text{Alice}, \text{Bob}, \text{Charlie}, \ldots \}} \)

\(\text{Time}\) = \(\mathbb{R}^{\{\text{Monday}, \text{Tuesday}, \ldots, \text{Sunday}\}} \)

\(\text{Words}\) = \( \mathbb{R}^{\{\text{Math}, \text{Sports}, \text{Movie}, \ldots\}} \)

Algebra for tensor decompositions

Source: Optimal Search Spaces for Tensor Problems, Figure 1.1

Adjoints detect

Derivations detect

Source: Detecting cluster patterns in tensor data, Figure 3

Product decomposition via algebra

1

2

3

4

5

No product decompositions?

Efficient computation

Asymptotic improvement to complexity of solving for \( \text{Der}(*) \)

  Target: \( O(n^6) \) to \( O(n^{4.5}) \) for \( \text{Der}(*) \) of cubic tensors

Tensor decomposition

Generalize existing tensor decompositions to products of tensors

  Target: Computable characterizations of product indecomposability

Proposal Summary

Efficient algorithm for computing the Adjoint Algebra

(Continuation from CSU Qualifying Exam, Part B)

Given

Find

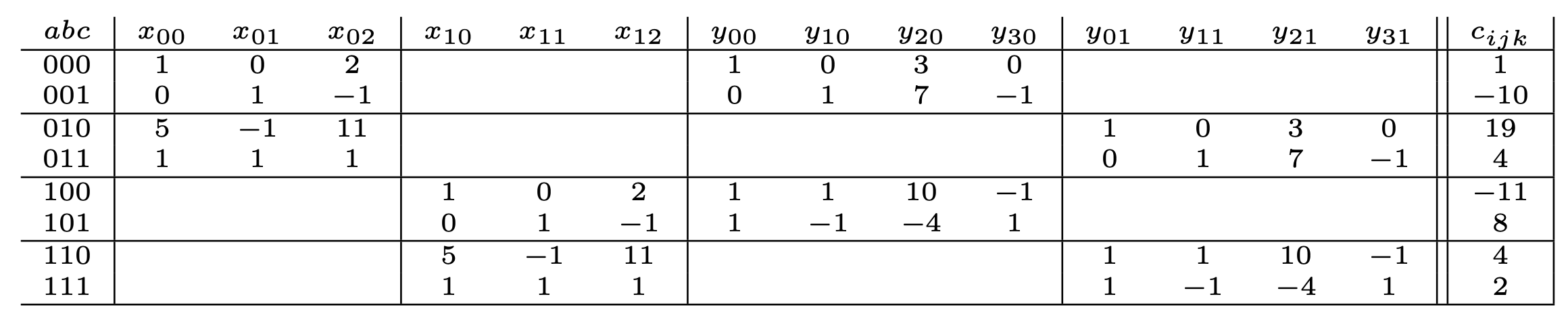
Interwoven striding in augmented matrix

> t := Random(KTensorSpace(GF(997), [20,20,20]));
> Nucleus(t,1,2);
Constructing a 800 by 8000 matrix over Finite field of size 997.
Computing the nullspace of a 800 by 8000 matrix.
Matrix Algebra of degree 40 with 1 generator over GF(997)

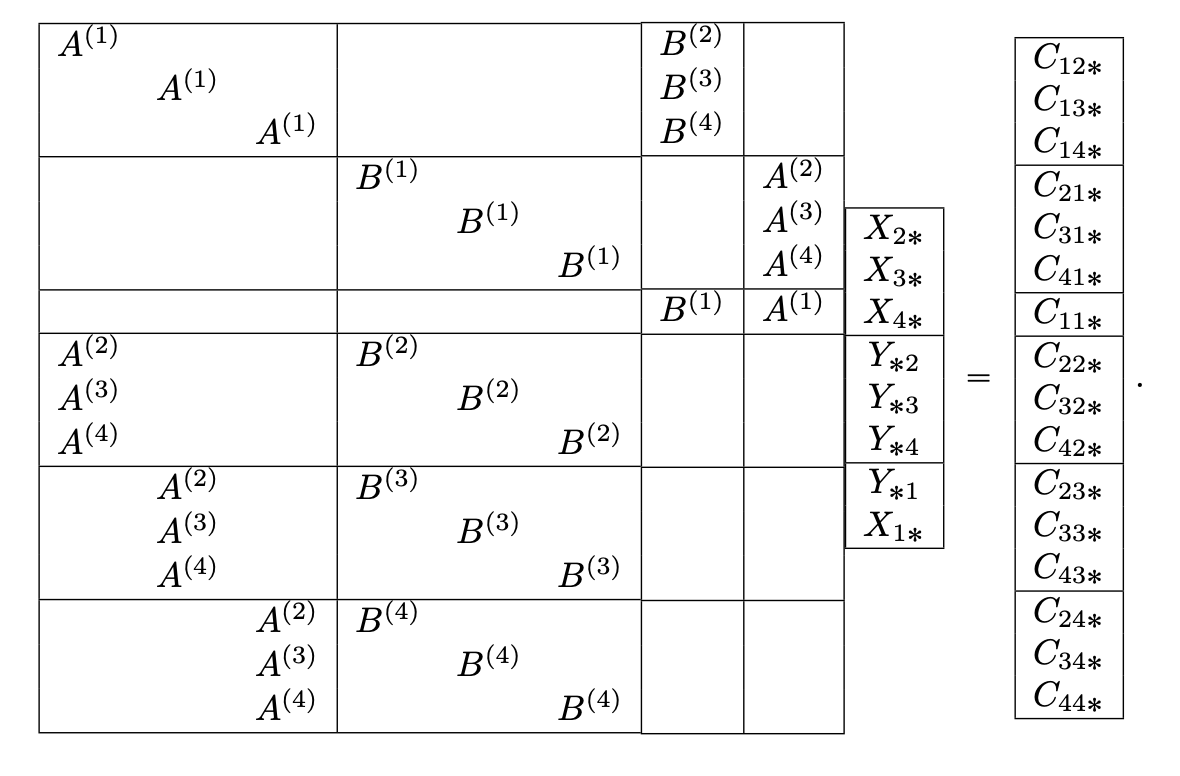
More efficient than solving full flattened system

Dense system after clearing

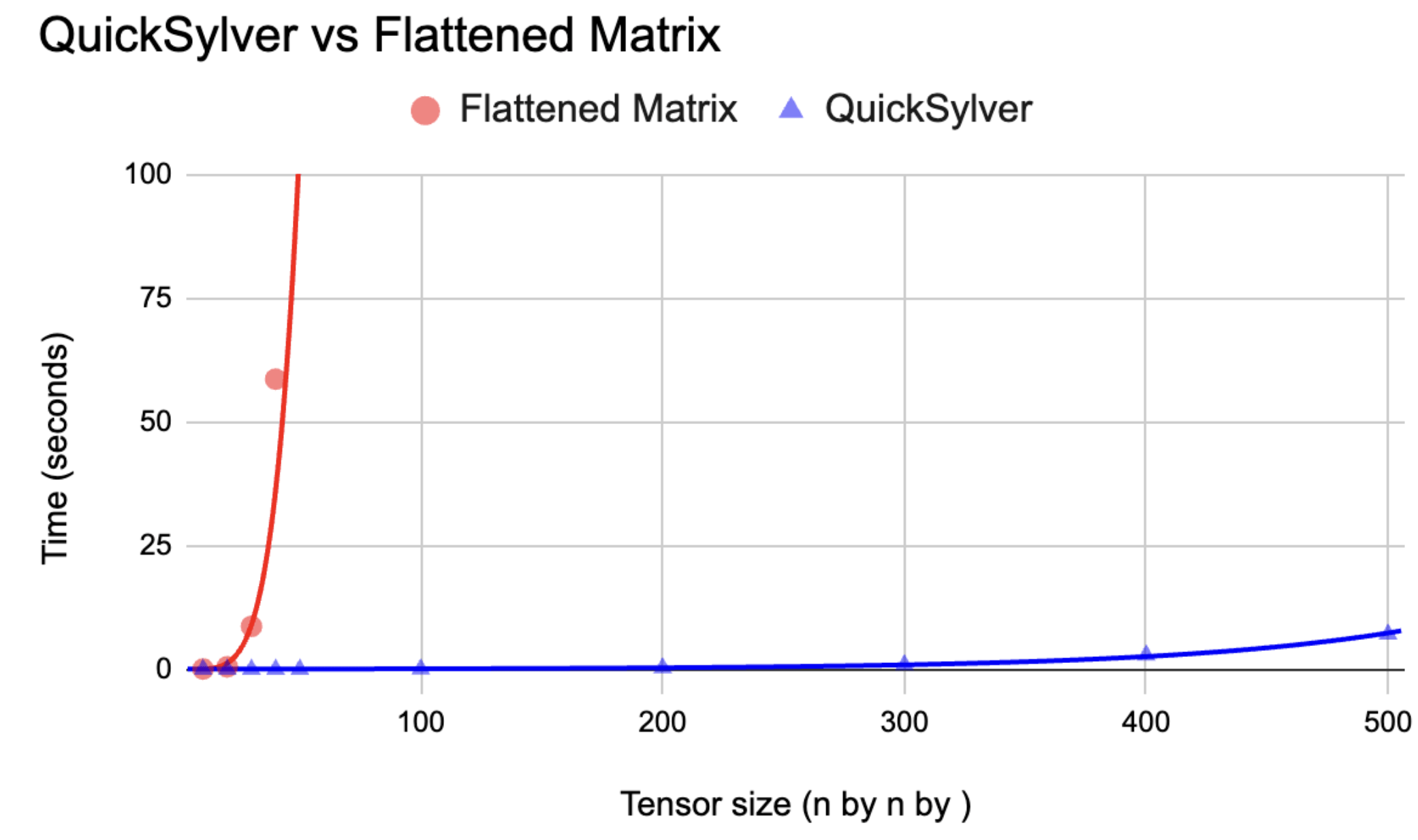
\( O(n^3) \) for QuickSylver. \( O(n^6) \) for flattened matrix to compute single solution

Distilling the idea 

Let \(A,B,C,R,S \) vector spaces, with fixed isomorphisms to dual.

View \( r: R \rightarrow B \otimes C, s: S \rightarrow A \otimes C \) through isomorphisms to dual

Find \( A' \leq A, B' \leq B \) of small dimension that split monomorphisms

\( \tilde{r} : R \hookrightarrow B' \otimes C\) and \(\tilde{s} : S \hookrightarrow A' \otimes C \)

Dissertation Proposal

Efficient algorithm to compute Derivation Algebra

Goal: Asymptotic improvement from \( O(n^6) \) flattened linear system solution for \( \text{Der}(*) \)

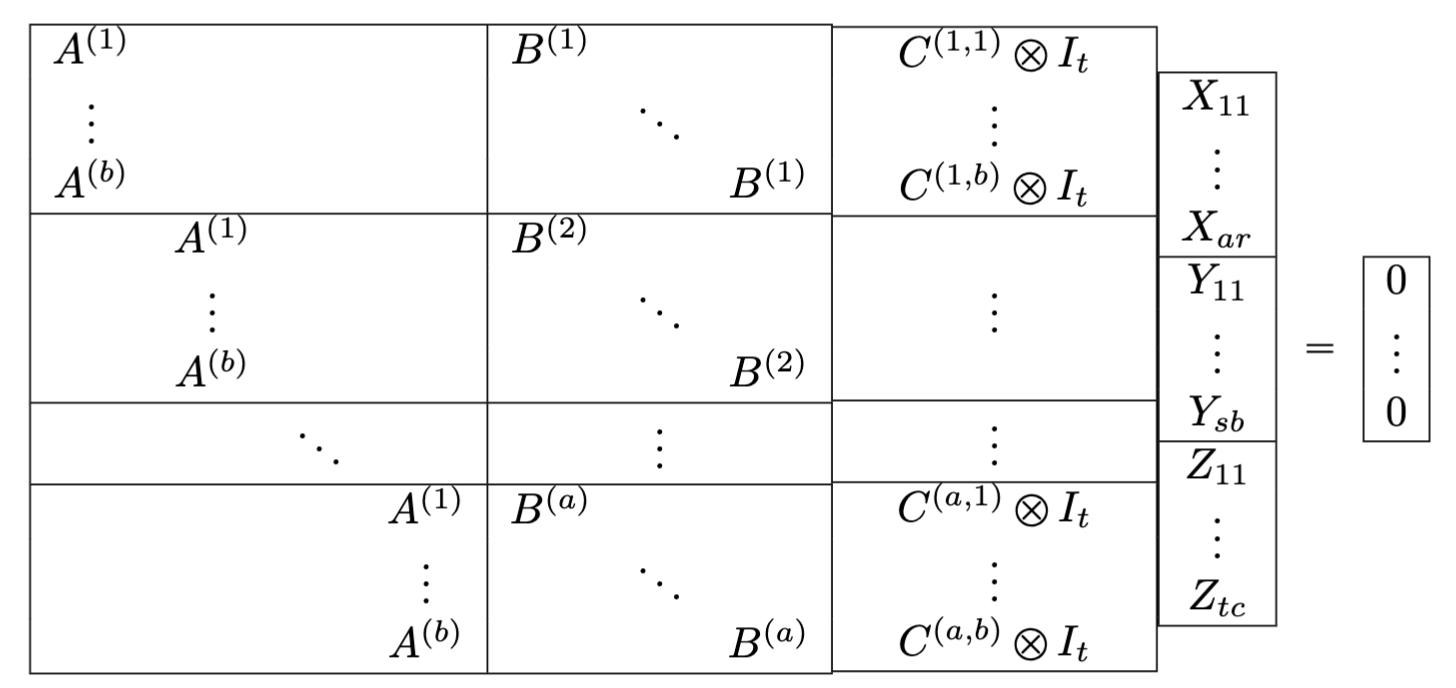
Tiny Example shows more interwoven striding

\( \text{Der}(t) \) is nullspace of 

> t := Random(KTensorSpace(GF(997), [20,20,20]));
> DerivationAlgebra(t);
Construting a 1200 by 8000 matrix over Finite field of size 997.
Adding in possible fusion data.
Computing the nullspace of a 1200 by 8000 matrix.

Use idea from Sylvester

Let \(A,B,C,R,S, T \) vector spaces, with fixed isomorphisms to dual.

Tensor product

Let \( A, B \) be unital associative \( K \)-algebras

Observation: \( A \otimes B \) is a K-algebra, with multiplication
\[ (a \otimes b)(c \otimes d) = ac \otimes bd \]

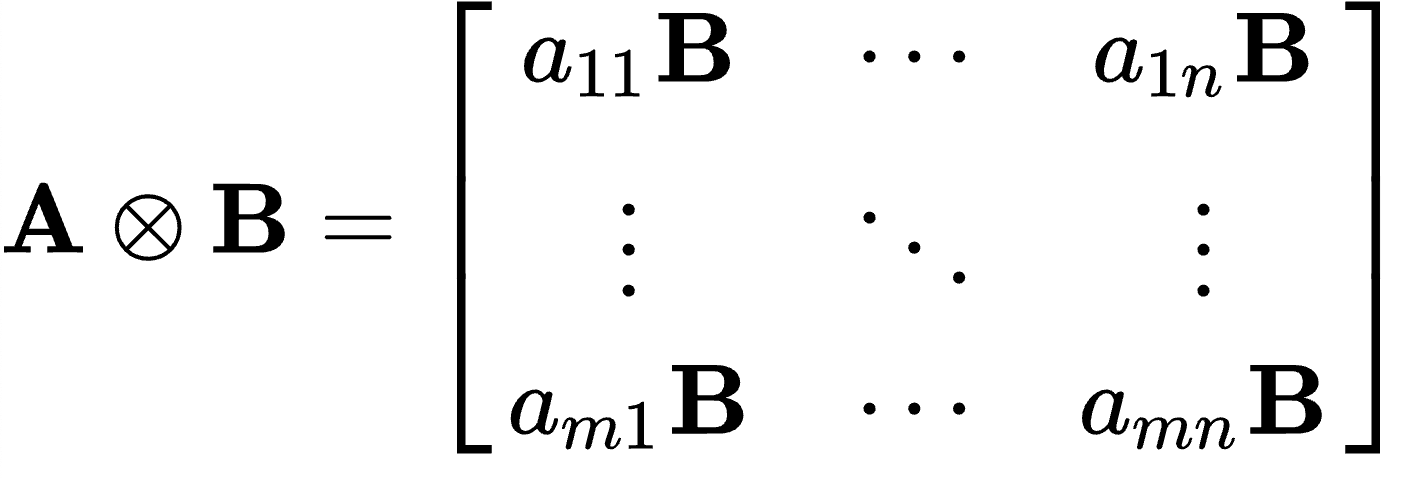
For \( s: U \times V \rightarrowtail W \) and \(t: X \times Y \rightarrowtail Z \)

Define \( s \otimes t: (U \otimes X) \times (V \otimes Y) \rightarrowtail (W \otimes Z) \) as
\[ \langle s \otimes t | u\otimes x, v \otimes y \rangle = \langle s | u,v \rangle \otimes \langle t | x,y \rangle \]

Tensor product of bilinear maps

Extend to bilinear maps

Let \(s: K^2 \times K \rightarrowtail K^2 \) and \( t: K \times K^3 \rightarrowtail K^3 \) both be bilinear maps corresponding to scaling vectors by \( K \)

Example

Arbitrary valence​

Let \( s: U_n \times \cdots \times U_1 \rightarrowtail U_0 \) and \( t: V_n \times \cdots \times V_1 \rightarrowtail V_0 \)

Define \( s \otimes t: (U_n \otimes V_n) \times \cdots \times (U_1 \otimes V_1) \rightarrowtail (U_0 \otimes V_0) \) as

\[ \langle s \otimes t|(u_i\otimes v_i)_{i=1}^{n} \rangle = \langle s| u_n,\ldots, u_1\rangle \otimes \langle t |v_n, \ldots, v_1\rangle \]

Dissertation Proposal

Computable characterizations for product decompositions

Definition

Given \( r: U_n \times \cdots \times U_1 \rightarrowtail U_0 \), we say \(r\) has a Kronecker decomposition into a finite set \(\mathcal{S}\) if

\[ r \cong \bigotimes_{s \in \mathcal{S}}s \quad \text{for } s: V_{s,n} \times \cdots \times V_{s,1} \rightarrowtail V_{s,0} \]

r is Kronecker indecomposable if \( r \cong \bigotimes_{s \in \mathcal{S}}s \) implies \( \mathcal{S} \subset \{r, \mathbf{1} \}\), where \(\mathbf{1}: K \times \cdots \times K \rightarrowtail K \) is \(K\)-multiplication tensor.

Add to existing corpus of decompositions

a = bc means \( \mathbb{M}_a(K) \cong \mathbb{M}_b(K) \otimes \mathbb{M}_c(K) \)

Example 1: Kronecker product of matricies

Example 2: Associative algebras

\( \mathbb{H} \otimes_{\mathbb{R}} \mathbb{C} \cong \mathbb{M}_2(\mathbb{C}) \)

Example 3: Away from associative algebras

Let \( K^3 \) spanned by \( \{ e,f,h \} \), and \( s: K^3 \times K^3 \rightarrowtail K^3 \) be the tensor given by
\[ \langle s | e,f \rangle = h \\ \langle s | e,h \rangle = -2e \\ \langle s | f,h \rangle = 2f \]

and \( \langle s | u,v \rangle = - \langle s | v,u \rangle \)

Preliminary\({}^{1}\) Results

Definition [Derivation Closure] (First, Maglione, Wilson '20)

\( (| t |)  = \{ s: U_n \times \cdots \times U_1 \rightarrowtail U_0 \mid \operatorname{Der}(t) \subseteq \operatorname{Der}(s) \} \)

\({}^1\) Pun maybe intended

Using Corollary to decide isomorphism

Let \(s: K^3 \times K^3 \rightarrowtail K^3 \) be the \( \mathfrak{sl}_2 \) multiplication tensor.

Fact: \( \text{dim}(| s |) = 1 \)

Bowtie tensor is indecomposable?

Recall the bowtie tensor \( r: K^5 \times K^5 \rightarrowtail K^5 \) has entry \(1 \) at \((1,2,3)\), \((1,4,5)\), and all its permutations

Fact: \( \text{dim}(| r |) = 4 \)

Definition [\( (P,\Omega) \)-product] (First, Maglione, Wilson, '20):  
Let \( U_n, \ldots, U_1 \) be vector spaces, \( P \subset K[x_n,\ldots, x_1] \), \( \Omega \subset \prod_i \operatorname{End}(U_i) \)

Other products

\((P,\Omega)\)-products are the starting point for non-Kronecker decompositions of tensors.

Questions?

TODOS:

1. Outer action definition make it easier to read/understand
2. "Kronecker indecomposable"
3. Describe goals in start slides and ensure it's standalone
4. More than just sl2 example for lie product decomp
5. "smaller" meaning when describing kronecker decompositions
6. More pictures, consistent notation (avoid multilinear and hom and...)
7. Point to slides, no hoodie, don't put hands in pocket
8. \Xi(P,\Omega): Better intuition on the subspace - talk about it
9. Mention "Brauer" for associative algebras
10. Maybe add the bowtie tensor example?
11. Describe fact that an infinite family has 1D densor for a fixed Lie algebra
12. Pic/example of 2x2x2 system?
13. Full tensorOverCentroid example in writeup

TODOS May 1

1. Theorem authorship credit folklore a bit more rather than an exact one
2. Move problem first in derivation question
3. "Given, Return" question set up for der closure
4. Colors for equations
5. Sylvester equation composition notation fix up using iotas
6. Tiny der example: stride it out with some non-standard numbers
7. Avoid "believe" or "hope" words
8. Tensor product of algebras -> go down to regular old tensor products of things with a product structure like a ring
9. Outer product tensor make into pictures to be less wordy
10. Drawing use tikz or some non-hand drawn tools
11. Derivation equation flattened: typeset it a bit better
12. Indecomposable: more precise language, new notation
13. "other products" - tighter language, mention "parametrized", combinatorics
14. (P,\Omega) products - mention interpretation challenges
15. Start and end with bowtie example
16. Splitting verbal emphasis on Quaternions tensor C having zero divisors example

Clearing and backsubstitution algorithm translates to finding \( A' \leq A, B' \leq B \) such that \[ (\pi_{A'} \otimes I_C) \circ r \] and \[ (\pi_{B'} \otimes I_C) \circ s \] have left inverses

Given 3 bilinear maps \[ r: U_2 \times U_1 \rightarrowtail U_0 \\ s: V_2 \times V_1 \rightarrowtail V_0 \\ t: W_2 \times W_1 \rightarrowtail W_0 \]

SKIP!

Coordinatized

Definition: (Outer action)
Let \( t \in K^{a \times b \times d} \) given as \( [t_1,\ldots, t_d] \), each an \( a \times b \) matrix, let \( Z \in \mathbb{M}_{d\times c}(K) \)

The outer action of Z on t is \( t^Z \in K^{a \times b \times c} \) given as \( [(t^Z)_1, \ldots, (t^Z)_c] \), where \( (t^Z)_j = \sum_i t_i Z_ij \)

SKIP!

Theorem (Brooksbank, Maglione, Wilson '21)

1. There are an infinite family of tensors t with \( \text{dim} (| t |) = 1 \)

2. Given \( s, t: U \times V \rightarrowtail W \) with \( \text{dim} (| s |) = 1 \) and \( \text{dim} (| t |) = 1 \), over big enough fields,

Deciding \( s \cong t \) is polynomial in \( \text{dim}(U + V +W) \)

\( (| * |)  = \{ s: U \times V \rightarrowtail W \mid \operatorname{Der}(*) \subseteq \operatorname{Der}(s) \} \)

Skip!

Extend to higher valence tensors

\( \operatorname{Nuc}_{32}(t) = \{ (X,Y) \mid \langle t|Xu_3, u_2, u_1 \rangle = \langle t | u_3, Yu_2, u_1 \rangle \)

\( \operatorname{Der}_{321}(t) = \{ (X,Y,Z) \mid \langle t|Xu_3, u_2, u_1 \rangle + \langle t | u_3, u_2, Yu_1 \rangle = \langle t | u_3, u_2, Zu_1 \rangle \)

SKIP!