基礎演算法們
aka 東西一堆

\(ALGO\ [4]\ [5]\) 失蹤

這好像是我最後一堂小社掰掰

\(INDEX\)

枚舉
剪枝
greedy
雙指針
分治
二分搜

其實我是連結喔

這我

20729 蔡嘉晉
失蹤的世宗
judging

因為大家都用之前的綽號講爛梗所以換綽號了
但還是一樣爛
這邊推薦大家叫我本名

店言學術
資訊校隊墊底
北市賽佳作 rank24 爛透了哭

題外話

上上禮拜應該有教一個資料結構
它叫做deque
- 一個可以雙向插入刪除的queue
那它該怎麼唸呢
- di-Q
- deck

顯然是di-Q
因為它是double ended queue
不要扯甚麼那個字按照發音該念deck 它就是念di-Q
這邊不接受異議
btw這場爭吵在資訊小圈圈從來沒停過就是了所以 di-Q

題外話 - 2

如果用windows看這份簡報
可能會看到一些很像 ** 的栗子
但他在mac是長這樣的
所以他是栗子

{enumeration}

枚舉就是暴搜啦哈哈哈

然後我不會北市賽的三等獎就沒了哈哈

枚舉誰不會

我不會
反正就把所有情況列出來啊很難嗎
聽起來蠻簡單ㄉ
但你真的會枚舉嗎

但你真的會枚舉嗎

沒事

我只是覺得動畫很好玩

一顆常見的🌰

給你一個長度為10的陣列
請輸出所有子序列
- 子序列定義為不必且包含原陣列部分元素的陣列
- e.g.{1, 2, 3}的子序列{∅},{1},{2},{3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}
- 這邊假設所有元素相異
可以發現會有 \(2^n\) 個子序列
- 因為對每個元素你有拿或不拿兩種選擇
so how to enumerate
又是位元運算!

how to do

既然會有 \(2^n\) 種子序列
那就把他們編號成 \(0\) ~ \(2^n-1\) 吧
每個數字代表一個唯一的子序列

你會發現 \(0\) ~ \(2^n-1\) 會是一個n個位元的整數的所有數字
00000000 代表 0
111111111 (n個) 代表 \(2^n-1\)
每個數字對應一個子序列！！！！！！！
如果一個數字在二進位下的第 \(i\) 個字元是1
那就拿 \(a_i\)
如此便會窮舉到所有的子序列了
🌰的🌰在下一頁

🌰的🌰

有一個陣列 {1, 2, 3}
\(0\) ~ \(2^3-1\)
全部的子序列被枚舉出來了欸

數字	二進位數字	子序列
0	000	{∅}
1	001	{3}
2	010	{2}
3	011	{2, 3}
4	100	{1}
5	101	{1, 3}
6	110	{1, 2}
7	111	{1, 2, 3}

#include <bits/stdc++.h>
using namespace std;
#define int long long

signed main(){
    int n;cin>>n;
    vector<int> arr(n);
    for(int i=0; i<n; i++) cin>>arr[i];
    for(int i=0; i<(1<<n); i++){  //從0-(2^n-1)
        for(int j=0; j<n; j++){
            if((i>>j)&1) cout<<arr[j]<<' ';
            //how to 檢測某個數字的第j個字元是不是1?
            //把他右移j次 讓那個字元變成最小的那一位
            //最後位元且 1 這樣如果那位是1 回傳1 否則0
        }cout<<'\n';
    }
}

# 位元枚舉

位元枚舉

位元運算好噁心

也可以用遞迴去枚舉la
怎麼搞?
對每個元素去枚舉要不要拿他
開個01陣列紀錄要不要取
選擇取 -> 遞迴到下個位元 -> 選擇不取 -> 遞迴到下個位元

#include <bits/stdc++.h>
using namespace std;

vector<int> take(1000, 0);
int n;
void recur(int x, vector<int>& li){
    if(x==-1){
        for(int i=0; i<n; i++) if(take[i]) cout<<li[i]<<' ';
        cout<<'\n';
    }else{
        take[x]=1;      //這裡很重要
        recur(x-1, li); //這裡超重要
        take[x]=0;      //這裡要記得
        recur(x-1, li); //很多枚舉都要這樣寫
    }
}

signed main(){
    ios_base::sync_with_stdio(false);cin.tie(0);
    cin>>n;
    vector<int> li(n);
    for(int i=0; i<n; i++) cin>>li[i];
    recur(n-1, li);
}

#遞迴枚舉

遞迴枚舉

{enum-pruning}

來砍樹囉 (剪枝

~~來減肥囉 (減脂~~

決策樹

. . .

再講一下枚舉是甚麼

剛剛那顆決策樹
你會遍歷整顆樹的所有節點
用這些節點去獲得所求的答案
因為對每一種情況去做計算
所以叫做枚舉

但這樣顯然會TLE
看太多沒用的東西了
如果我們確定一個決策樹的小部分是沒用的
剪枝!
不要再看了

很煩的🌰

CSES 1625 Grid Paths
有一個7*7的方陣
要從 \((0, 0)\) 走到 \((0, 7)\)
每個格子恰經過一次
題目會給一個48字元的指令
指令中包括第 \(i\) 個動作要往上下左右哪一個
也有可能是 '\(?\)' 代表都可以
求共有多少組合滿足可以從 \((0, 0)\) 走到 \((0, 7)\) 的條件

哪裡煩呢
我的常數大了點於是乎 TLE 吃爆 -->

雖然我們還沒講圖論

但等下會示範一下怎麼在網格上走路

既然都是枚舉了就暴搜吧

紀錄每個點有沒有走過
對每個點進行一系列操作
- 標記這個點為已走過
- 往身旁每個還沒走過的點走
- 把自己的點重設回還沒走過
如果把整張圖走完並且到 \((0, 7)\) 代表得到一種可行方法
答案數加一
遞迴下去算正解

一定是對的除非你寫爛
超級慢超級
可能要跑十分鐘或更久

🌰的程式🌰

開一個二維陣列
紀錄哪些格子走過了
記得判有沒有超出邊界
可以開兩個陣列
處理上下左右走的問題

#include<bits/stdc++.h>
using namespace std;

int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};

vector<vector<int>> vis(9, vector<int>(9, 0));
//9是陣列分別的大小 0是陣列每一項的初始值

int cnt=0; //答案
string s; //指定操作
void enumerate(int n, int x, int y){
    //n 走幾步了 / x 目前走到的格子的x座標 / y y座標
    if(n==48&&x==7&&y==0){
       cnt++;
    }
    int op=-1; // operation 操作
    if(s[n]=='U') op=0;
    if(s[n]=='D') op=1;
    if(s[n]=='L') op=2;
    if(s[n]=='R') op=3; //分別照要求操作
    if(op!=-1){
        if(vis[x+dx[op][y+dy[op]]) continue;
        vis[x+dx[op]][y+dy[op]]=1; // 枚舉經典操作
        enumerate(n+1, x+dx[op], y+dy[op]);
        vis[x+dx[op]][y+dy[op]]=0;
    }else{ //無要求 可以自定義
        for(int i=0; i<4; i++){
            if(vis[x+dx[i]][y+dy[i]]) continue;
            vis[x+dx[i]][y+dy[i]]=1;
            enumerate(n+1, x+dx[i], y+dy[i]);
            vis[x+dx[i]][y+dy[i]]=0;
        }
    }
}

signed main(){
    cin>>s;
    for(int i=0; i<9; i++) vis[i][0]=1, vis[0][i]=1, vis[8][i]=1, vis[i][8]=1;
    //初始化 因為vis=1代表不能走
    //而我們要再(1, 1)~(7, 7)上走
    /所以把外圍的都先封掉
    //也可以避免走出陣列 RE
    vis[1][1]=1;
    enumerate(0, 1, 1);
    cout<<cnt;
}

x

y

觀察 - 0

既然都說要減脂了
再叫出決策樹一次
走到什麼樣的情況可以直接宣布這次模擬絕對不會成功？

. . .

觀察 - 1

如果已經走到終點了
但還沒走完48步
- 共49格
既然每格只能走一次
顯然不可能成功
所以就把他判掉

還是不夠快
但執行時間可能從十分鐘變一分鐘
已經差很多了
所以繼續優化

if(n==48){
    if(x==6&&y==0) cnt++;
    else return;
}

觀察 - 2

如果你走到一格
他只能往左右走但不能往上下走
或只能往上下走但不能往左右走
什麼意思？

有一邊一定走不到！
不可能是答案
剪掉

理論上剪完這個就能壓線ac了
自己練習看看ㄅ可能兩個if就行(?
TLE的話可以試試壓常數或繼續觀察(?

簡化一點點

只能往上下走但不能往左右走了

如果往上就永遠到不了終點

如果往下就永遠填不完上面的

小提醒

enum在c++是保留字
不要拿他來命名枚舉函式

~~會講這種東西一定是因為我做過這種事~~

題單的啦

NEOJ 資芽讚除了他oj的長相
- 62
  - 超級煩
- 63
  - 比較簡單
CSES
- 1624 Chessboard and Queens
  - 可以用剛剛枚舉陣列的方式試試
- 1625 Grid Paths
  - 剛剛ㄉ如果只有幾筆TLE可以找講師鴨腸

{greedy}

要叫他貪心還是貪婪呢

一個不用思考的🌰

一條數列有正有負
可以拿走部分的數字
希望拿到的數字的總和最大

啊不就看到正的就拿
對啊就這樣
貪婪的拿走所有能讓你答案更好的東西

當然正常來說不會這麼水

how to greedy

用greedy算法的時候
不是要找到一個最佳解
而是要往一個不會比最佳解差的方向走
也就是說你做某個操作
你不確定他的結果
但是你知道這樣還是能夠達到最佳解
這樣把所有要操作的東西處理完
因為你每次都維護著最佳解
所以最後答案就會是好的

好抽象圖形化一下

再看決策樹

想像枚舉的🌰
每個選擇就像在一棵樹上做決策
每個樹上的點分別代表一種決策
用剛剛拿陣列當🌰 假設有一個陣列{1, -3, 2, 4, -6}

根

0

1

1-3

1

1+2

1

3-4

3

3-6

3

this one

is good

¿SO?

在決策樹中
greedy要做的不是找到所有最佳解可能存在的枝葉們
而是要保證往下走的這顆子樹會有至少一個最佳解

根

0

1

1-3

1

1+2

1

3-4

3

3-6

3

this one

is good

來看個真正的greedy🌰

眾所皆知建電每次出去吃飯都會有些人吃飯特別慢
比如吉米每次都在講話然後花了別人兩倍時間才吃完
所以上菜及吃飯的先後順序就很重要了

TIOJ 1072 誰先晚餐
給定每個人點的餐所需要的做菜時間 \(W_i\) 以及吃飯時間 \(C_i\)
有一廚師專門為這桌人服務
求最快何時所有人都能吃完飯

誰要先吃？
做飯快的? 做飯慢的? 吃飯慢的? 吃飯快的?

證明啊

生活中我們可能會讓吃比較慢的人先吃 (\(C_1 \ge C_2 \ge ... \ge C_N\))
但為什麼證明啊你證明啊
若一吃飯序列中非全由吃較慢的人先吃
必有二相鄰吃飯者其 \(C_i \lt C_{i+1}\)
意即 \(i+1\) 吃比 \(i\) 慢
考慮這兩個人誰該先吃

\(i\) 先吃

\(i+1\) 先吃

\(i\) 耗時

\(i+1\) 耗時

\(W_{i+1}+C_{i+1}\)

\(W_i+W_{i+1}+C_{i+1}\)

\(W_{i}+C_{i}\)

\(W_i+W_{i+1}+C_{i}\)

>

\(i+1\) 先吃的情況一定不比 \(i\) 差

#include <bits/stdc++.h>
using namespace std;
#define ss second
#define ff first
#define int long long
signed main() {
    ios_base::sync_with_stdio(false);cin.tie(0);
    int n;
    while(true){
        cin>>n;
        if(n==0) return 0;
        vector<pair<int, int>> people;
        for(int i=0; i<n; ++i){
            int a,b;
            cin>>a>>b;
            people.push_back({b, a});
        }
        sort(people.begin(), people.end(), greater<pair<int, int>>()); 
        // pair會先比較第一項再比較第二項
        int current=0; //廚師煮飯時間和
        int maximum=0;
        for(int i=0; i<n; ++i){
            current=current+people[i].ss; 
            maximum=max(maximum, current+people[i].ff); // curTime + arr[i].first是第i人離開的時間
        }
        cout<<maximum<<'\n';
    }
}

# PRESENTING CODE

AC CODE

{greedy-2}

為了不要讓上一條太深

🌰 - 2

蘿莉切割問題 ~~每次greedy都一定要講~~
原版題序偏噁和諧版如下
把一個東西分成 \(N\) 塊
每塊有一個權重將一塊重量為 \(x\) 的東西分成 \(y\), \(z\)
需花費 \(x\) 的代價
已知所需分成的 \(N\) 塊個別所需的權重求最小代價

例：
一塊東西要分成 3 2 2 3 代表原本有十單位
可以 [10] -> [8, 2] -> [5, 3, 2] -> [3, 2, 3, 2] 代價 10+8+5 = 23
或是 [10] -> [6, 4] -> [3, 3, 4] -> [3, 3, 2, 2] 代價 10+6+4 = 20
第二種顯然比較好，同時也是所有分割方法的最佳方法

耗

正著切太難做了不如反過來將想要切成的塊數合併吧
用一顆樹來解釋
- 不是決策樹

樹

序列: [8, 2, 3, 7, 5]
btw這是一顆二元樹

2

3

5

10

15

7

8

25

合併 / 切割

樹

這樣代價是多少？
(2+3)+(5+5)+(7+8)+(15+10)

2

3

5

10

15

7

8

25

樹

這樣代價是多少？
(2+3)+((2+3)+5)+(7+8)+((7+8)+(2+3+5))
2 三次
3 三次
5 二次
7 二次
8 二次

2

3

5

10

15

7

8

25

樹

越底層的節點會被算到最多次
如果把最後結果當作第0層
他下面兩顆當第1層
第 \(i\) 層的要算 \(i\) 次

2

3

5

10

15

7

8

25

樹

所以我們要把越小的數字放越下面
最下層的會先算到才能算上層的
所以每次選最小的兩個來算!

也可以發現將樹上任二
葉節點交換皆會使答案
不變或增加

葉節點的意思是下面沒有東西的節點
7 8 2 3 5

2

3

5

10

15

7

8

25

證明？

可以發現每次都拿最小的兩個來算就好了
既然剛剛用樹來解釋了
所以樹歸
數學歸納法

證明

當 \(N = 2\)時，我們只有兩個數字\(a_1\)和\(a_2\)。，我們會先合併這兩個數字，成本為\(a_1+a_2\)，最終只剩下一個數字，所以成本最小。
假設對於\(N = k\ (k \ge 2)\)的情況，我們的貪婪策略總是能夠最終只剩下一個數字，並且成本最小。
歸納步驟：現在考慮\(N = k + 1\)的情況，我們有\(k + 1\)個數字\(a_1, a_2, ..., a_{k+1}\)。根據貪婪策略，我們會先合併a1和a2，成本為\(a_1+a_2\)
然後，我們得到了\(k\)個數字\(a_1+a_2, a_3, a_4, ..., a_{k+1}\)。根據歸納假設，可以使用貪婪策略將這\(k\)個數字合併成一個數字，並且成本最小
因此，總成本為\(a_1+a_2+\) 最小成本（\(k\)個數字的合併成本）
由於我們每次合併都是選擇最小的兩個數字，所以最小成本(\(k\)個數字的合併成本）也是最小的。因此，總成本最小。
綜上所述，我們使用貪婪策略可以確保最終只剩下一個數字，並且成本最小。這就是這個問題的一個有效解法。

#include <bits/stdc++.h>
using namespace std;
#define int long long

signed main(){
    int n,m;
    while(cin>>n){
        priority_queue<int,vector<int>,greater<int> > p;
        while(n--){
            cin>>m;
            p.push(m);
        }
        int sum=0;
        int a,b;
        while(p.size()>1){
            a=p.top();
            p.pop();
            b=p.top();
            p.pop();
            sum+=a+b;
            p.push(a+b);
        }
        cout<<sum<<'\n';
        p.pop();
    }
}

# 誰先晚餐

AC CODE

記得開long long

{greedy-3}

additional

如果有時間再講

最大線段覆蓋

在一個數線上
有 \(N\) 個區間
請取出最多的區間使所有區間不互相覆蓋

greedy的對區間右界排序並能拿就拿
why?

可以試試看用數歸或反證法證明

題單

ISCOJ
- 4455 整理河內塔
- 4507 星冰樂買一送一
CSES
- 1094 Increasing Array
NEOJ
- 70 / 74 / 78 / 89 / 91
CF
- 1894D Neutral Tonality
- 或是你可以查整個類別

{binary search}

競程是一半的二分搜跟一半的低批

--不知道誰說的

但我比賽都寫圖論題欸

--cjtsai

繼續從🌰講起

來玩猜數字遊戲 (TIOJ 1044
答案是1-100其中一個
每次猜會得到太大或太小其中一個結果
怎麼猜?
- 1-100都猜一次
  - 也太慢
- 10 20 30 40 直到猜到太大的再一個一個猜
  - 可以推廣到 n 位數就先 \(10^{n-1}, 2*10^{n-1}\) 來猜
  - 複雜度 \(O(10*log_{10}{n})\)
  - 好像還行
  - 更快一點?

二分搜

每次都對可能的區間砍半詢問

假設你問到 10 太小 60 太大
(10+60)/2 = 35
下一個就問35!
為什麼這樣比較好
60-35=25 / 35-10=25
不管怎樣都能至少淘汰掉一半的選擇

保證演算法的穩定性
複雜度?
\(O(log\ n)\)

看動畫

100太多了用10個示範一下
答案是4
一開始可能的答案區間顯然是全部 1 - 10

可能的區間
- 左界 1
- 右界 10
- 中間 (1+10)/2 = 5

1

2

3

4

5

6

7

8

9

10

看動畫

100太多了用10個示範一下
答案是4
一開始可能的答案區間顯然是全部 1 - 10

可能的區間
- 左界 1
- 右界 5
- 中間 (1+5)/2 = 3

1

2

3

4

5

6

7

8

9

10

Query(5) => 太大

看動畫

100太多了用10個示範一下
答案是4
一開始可能的答案區間顯然是全部 1 - 10

可能的區間
- 左界 3
- 右界 5
- 中間 (3+5)/2 = 4

1

2

3

4

5

6

7

8

9

10

Query(3) => 太小

看動畫

100太多了用10個示範一下
答案是4
一開始可能的答案區間顯然是全部 1 - 10

可能的區間
- 左界 3
- 右界 5
- 中間 (3+5)/2 = 4

1

2

3

4

5

6

7

8

9

10

Query(4) => ANS!

有什麼性質？

在 我們算到答案的時候
也就是答案所在的地方
有什麼變了？
query所給的值！

假設我們把 \(i\le ans\) 的query結果當1
把 \(i\gt ans\) 的query結果當0

1	2	3	4	5	6	7	8	9	10
1	1	1	1	0	0	0	0	0	0

Num

Query

所求

有什麼性質？

我們要找的東西在 0 1 交界！
and?
一開始全部都是1 後面全都是0
我們稱這種性質為 單調性
二分搜便是建立在這種性質上才能成立喔

1	2	3	4	5	6	7	8	9	10
1	1	1	1	0	0	0	0	0	0

Num

Query

所求

單調性

00000001111111 / 11111000000000 / 0000000000000
- 看起來就挺單調的對吧
0101010101000010100 / 01001001111010100 / 00000010000
- 看起來就有夠亂對吧

假設一個東西 00000011111
要找01交界
若戳到一個東西他是1 代表他右邊的全都是1 不用看了
- 可以理解成一種剪枝ㄅ
若戳到一個東西他是0 代表他左邊的全都是0 不用看了

單調性

但如果有個數列叫 1010100011101
如果你戳中間是1 顯然不能說右邊的都沒用
這就是沒有單調性

再講一次
有單調性才能二分搜喔
怎樣看出來有單調性？
- 可能是求第一個滿足條件的數
- 且在他之下不可能有東西滿足
- 且在他之上每個東西都能滿足
- 就可以考慮看看二分搜
- ~~或是那個題目的 N 一看就要帶 log~~

實作

有兩種常用的方法左閉右開 & 左閉右閉
左閉右閉
- [l, r]=1
- 維護一個可以是答案的區間
- aka 都是 1
- 我都寫這個
- 00000000001111111
- .............l.......r..........
左閉右開
- [l, r) = 1
- 維護的區間左界可以是答案
- 右界則是第一個不能是答案的
- aka \(l\) 是0 \(l+1 \sim r\) 是1

左閉右閉左閉右開

我推的二分搜

int l=0, r=MAXN;
while(r>l){
    int mid = (l+r)/2;
    if(check(mid)){
        r=mid;
    }else{
        l=mid+1;
    }
}

int l=-1, r=MAXN;
while(r-1>l){
    int mid = (l+r)/2;
    if(check(mid)){
        r=mid;
    }else{
        l=mid;
    }
}

所求為 l

最後 l 是最後一個 0

r 是第一個 1

兩種方法都各有人喜歡寫
但記得寫的時候不要混淆ㄌ
注意初始值避免被11111或00000卡掉ㄌ

聽幾次二分搜他就出現幾次

Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky. — Donald Knuth

小心不要寫爛掉ㄌ

{\(_2\)-search-2}

因為binary search-2打不下

這邊姑且把表示二進位的方法當作是個binary

對答案二分搜

你以為二分搜只能猜數字嗎
如果我們更改query或check函數決定01的方法
就能對其他東西二分搜ㄌ
有時候我們會發現題目要求的答案也具有單調性
這樣我們就可以 對答案二分搜 了
這也是題目中很常看到的東西

甚麼是答案有單調性?
題目可能要求最小的符合條件的數字
那就會是00000011111ㄌ
🌰

貼海報

在一個高低參差不齊的的牆壁上
要在同一個高度連續貼上n張長度分別為 \(a_1, a_2, a_3...\)的海報
問最高能貼在多高的地方

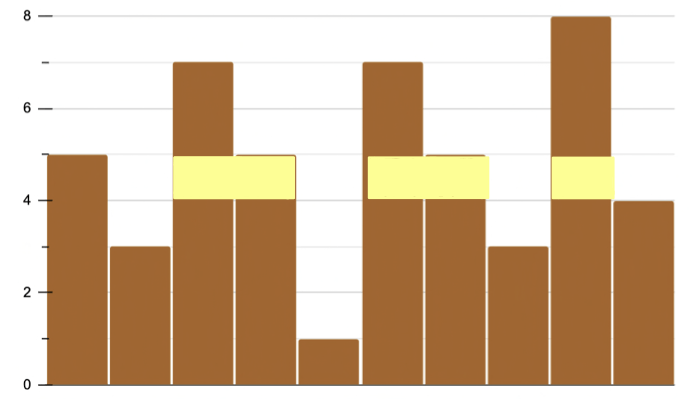
什麼東西有單調性

能貼的高度
因為越低的地方能貼的格子越多
如果高度 \(h\) 的地方能貼
\([0, h]\) 的高度一定都能貼

對 能貼的高度 二分搜
每次check花 \(O(N)\) 的時間檢查他可不可以用
就好了
總複雜度 \(O(N \ log C)\)
- C是 \(a_i\) 的值域

放個示意圖

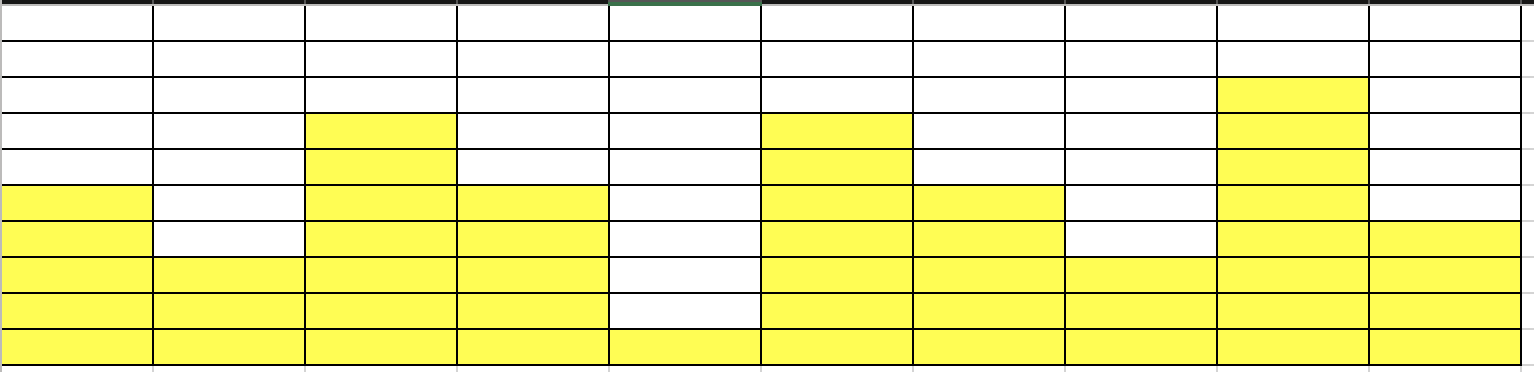
N = 牆壁長度 = 10
\(a_i\) = [2, 2, 1]
牆壁高度 = [5, 3, 7, 5, 1, 7, 5, 3, 8, 4]

什麼是較高的放得下較低的一定可以
how to 匹配 (確定某個高度可不可以)

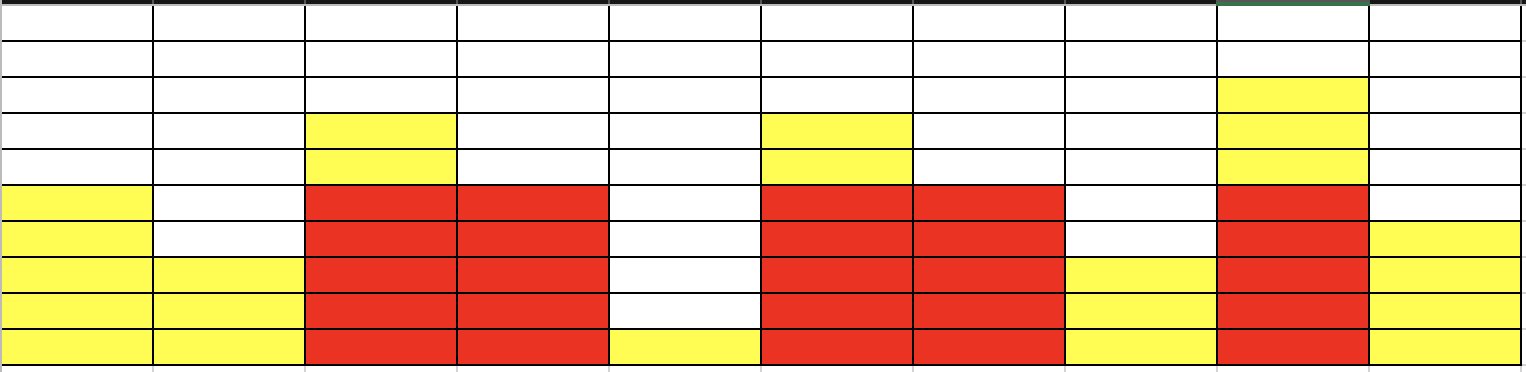
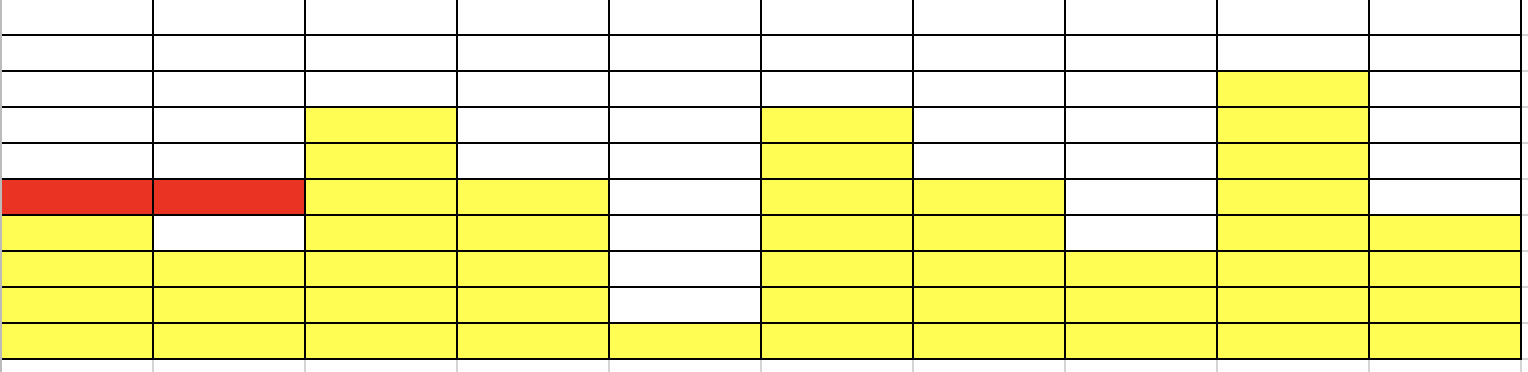
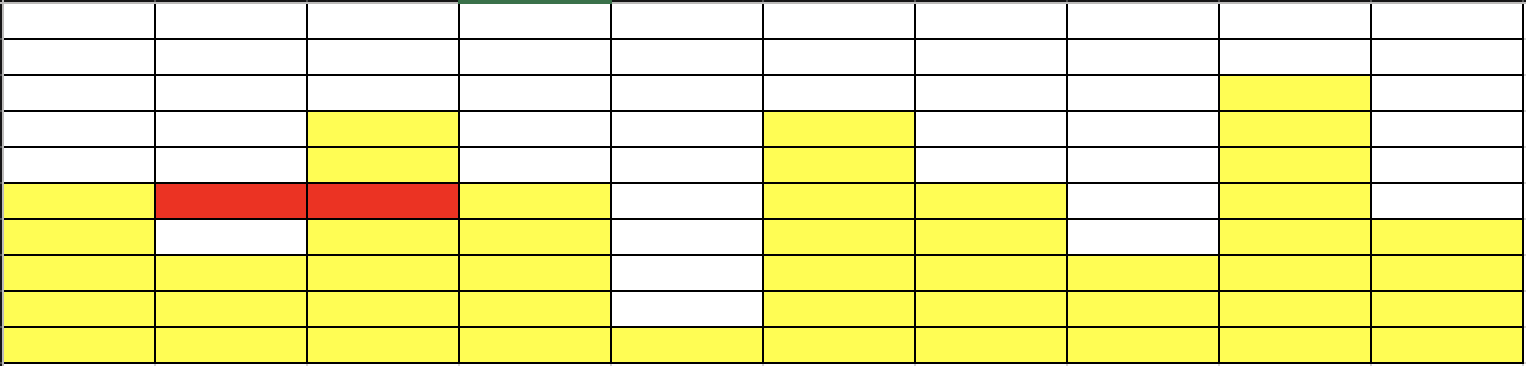
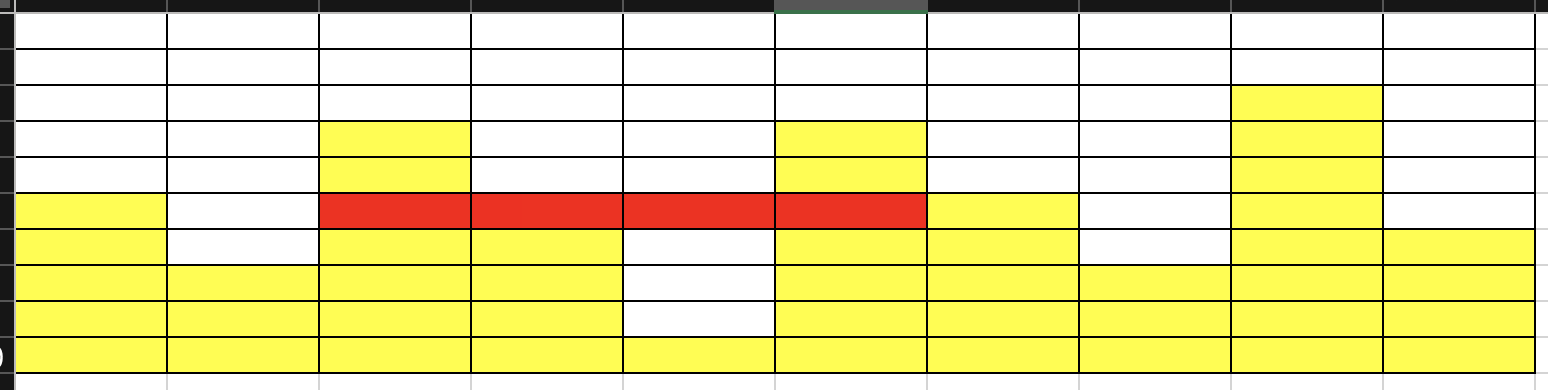
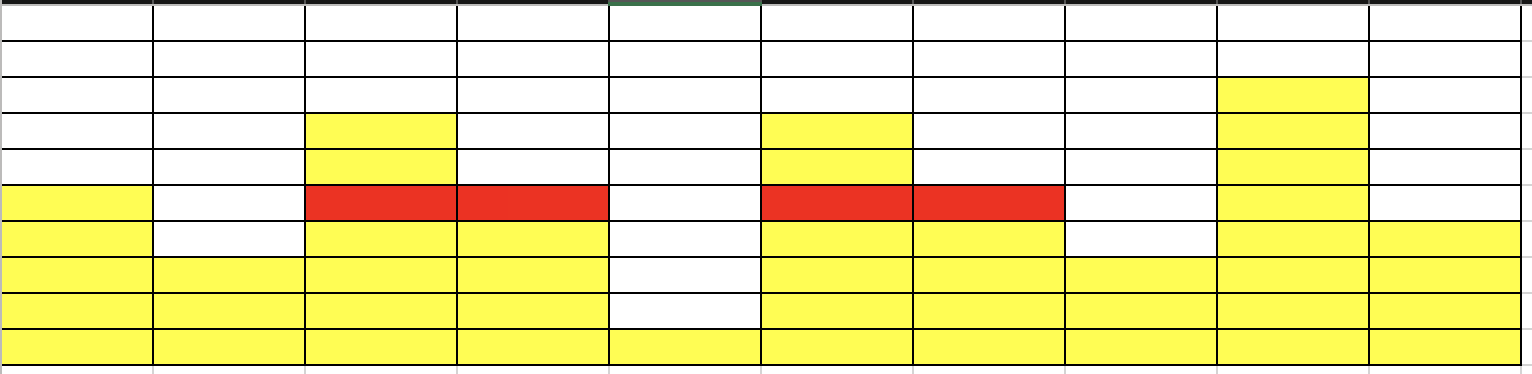
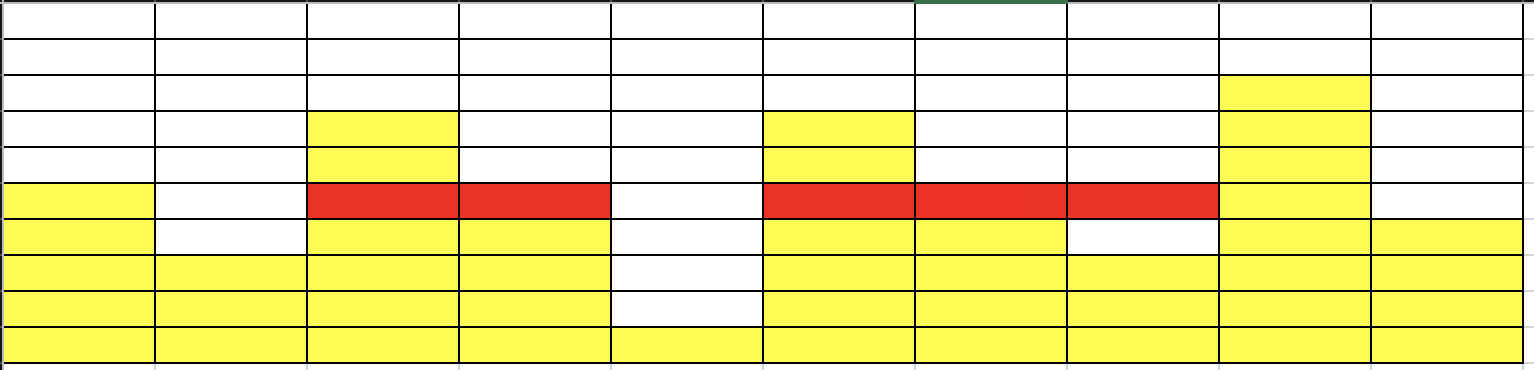
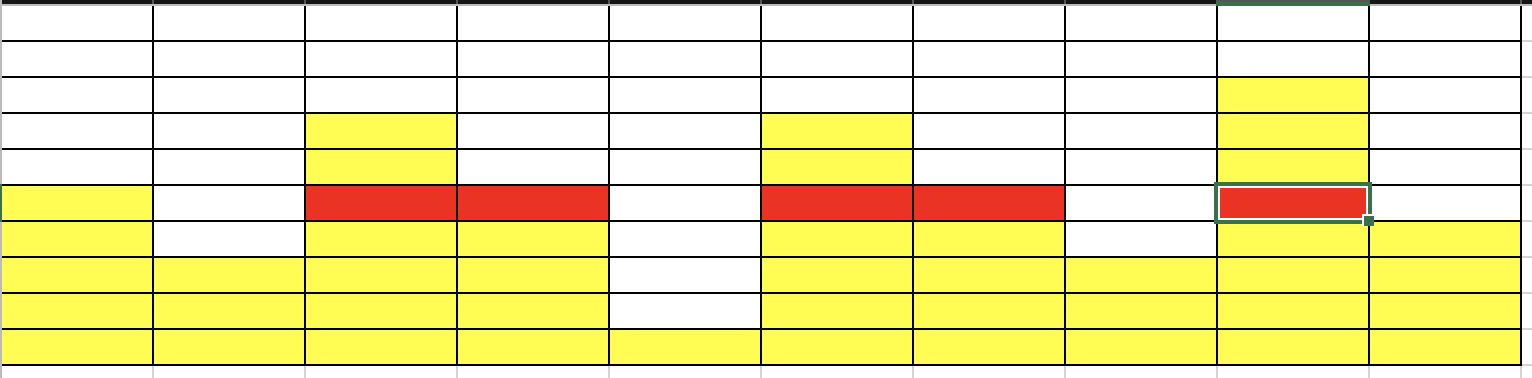
匹配成功！

畈叩

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 2e5 + 5;
const int KSIZ = 5005;
const int INF = 1e9+5;

int n, k;
int h[SIZE], w[KSIZ];

bool ok (int x) {
    int pos = 1, len = 0;
    for (int i = 1; i <= n; i++) {
        if (h[i] >= x) len++;
        else len = 0;
        if (len == w[pos]) {
            pos++;
            len = 0;
        }
        if (pos > k) return 1;
    }
    return 0;
}

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> h[i];
    for (int i = 1; i <= k; i++) cin >> w[i];

    int l = 1, r = INF;
    while (l < r) {
        int mid = (l + r) / 2;
        if (!ok (mid)) r = mid;
        else l = mid + 1;
    }
    cout << l - 1 << '\n';
}

Another 🌰

CF 1873E. Building an Aquarium
你要在一些珊瑚礁上蓋個魚缸
共有m單位的水
有珊瑚礁的地方不需要水且珊瑚礁為垂直向上生長
最高能蓋到多高

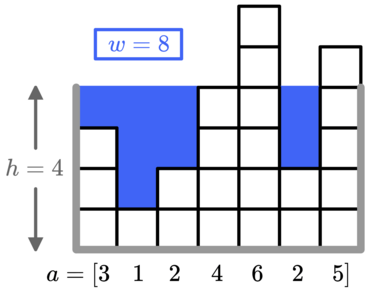
繼續對答案二分搜

\(O(log \ C)\) 對答案二分搜
\(O(N)\)檢查
- 掃過每個點看這裡的珊瑚礁有沒有比預期水面低
- 有的話就加上去
- 最後看會不會用超過 m 單位的水
\(O(N \ log C)\) AC

二分搜的話看到題目要想的是
- 什麼東西有單調性要對什麼東西二分搜
- check函數要怎麼寫
- 剩下實作模板記清楚就蠻好寫的ㄌ

畈叩

#include <bits/stdc++.h>
using namespace std;
#define int long long
int n, x;
vector<int> li(200007);

bool check(int h){
	int cnt=0;
	for(int i=0; i<n; i++){
		if(h>li[i]){
			cnt+=(h-li[i]);
		}
	}
	return cnt<=x;
}

signed main(){
	ios_base::sync_with_stdio(false);cin.tie(0);
	int t;cin>>t;
	while(t--){
		cin>>n>>x;
		for(int i=0; i<n; i++) cin>>li[i];
		int l=1, r=10000000007;
		while(l!=r-1){
			int mid=(l+r)/2;
			if(check(mid)){
				l=mid;
			}else{
				r=mid;
			}
		}cout<<l<<'\n';
	}
}

思考一下

ISCOJ 4451 田忌賽馬
- 你有 N 匹馬對手也有 N 匹馬
- 你的馬有初始數值跟每日成長數值
- 對手的馬則是固定的數值
- 問最少幾天後你的馬能贏至少k場
對什麼二分搜
什麼東西有單調性
想想看ㄅ

題單

zj b870 c575
CSES 1090 他被質疑了
NEOJ
- 60 69 73
TIOJ 1406
TOI初選好像蠻喜歡的
- 2021 pb TIOJ 2149
- 2023 pb zj k185

{divide & conquer}

分治分而治之

分治

解決大問題太困難了
我們先解決簡單的吧
\(O(N^2)\) 才能排好一個陣列
那我們先只排一半的陣列吧
現在有兩個排好的半個陣列了
- 好欸
然後呢
合併一下吧
既然兩邊都排好了
我去看兩邊的第一個誰小就是這陣列的最小的
第二小的則是在繼續看下去那邊的最小值比較小

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

2

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

2

3

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

2

3

4

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

2

3

4

5

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

2

3

4

5

6

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

2

3

4

5

6

7

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

2

3

4

5

6

7

8

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

2

3

4

5

6

7

8

9

兩個排好的半個陣列

來看動畫囉

1

3

4

6

8

2

5

7

9

10

1

2

3

4

5

6

7

8

9

10

合併排序 Merge Sort

這就是合併排序la \(O(N \ log N)\)
- 將一個陣列分成兩半
- 遞迴下去
- 合併
- 排序完了！
如果現在要排序的部分比較短
可以直接 \(O(N^2)\) 暴力排序ㄌ
畢竟分治常數比較大

飯叩

謝謝 @ckeisc_807

#include<bits/stdc++.h>
using namespace std;

void mergesort(int l,int r,vector<int> &data){
    if(r-l==1) return ;
    int mid=(l+r)/2,tmp_len=mid-l;
    mergesort(l,mid,data),mergesort(mid,r,data);
    vector<int> tmp(tmp_len);
    for(int i=0;i<tmp_len;i++) tmp[i]=data[i+l];
    for(int L=0,R=mid,i=l;L<tmp_len;i++){
        if(tmp[L]<data[R]||R==r) data[i]=tmp[L++];
        else data[i]=data[R++];
    }
    return ;
}
int main(){
    int n;
    cin>>n;
    vector<int> data(n);
    for(int i=0;i<n;i++) cin>>data[i];
    mergesort(0,n,data);
    for(int i=0;i<n;i++) cout<<data[i]<<" ";
    cout<<endl;
}

{D & C - 2}

分治好難

分治

所以分治到底是什麼
分而治之
分
- 把你要問的東西分成小東西
治
- 把小東西算完
合併
- 把小東西合併成大東西

分治用在哪
- 好合併的 / 小東西可以暴力做

快速冪

再來看一個比較簡單的分治
計算 \(a^n\)
\(n=10^{100}\)
- 通常會說要取模
- 不然怎麼輸出
怎麼算？
乘 n 次
- 完全是會TLE喔

快速冪(link

分
- 要算 \(a^n\)
- 那先算一半吧 \(a^{\frac{n}{2}}\)
治
- \(a^0=1\)
- \(a^1=a\)
合併
- if(n%2) //n是奇數
  - \(a^n=a^{\frac{n}{2}}*a^{\frac{n}{2}}*a\)
- else //n是偶數
  - \(a^n=a^{\frac{n}{2}}*a^{\frac{n}{2}}\)
這邊對 \(\frac{n}{2}\) 取下高斯 aka 無條件捨去到整數位

扣

遞迴式

迭代式

#include<bits/stdc++.h>
#define int long long
using namespace std;
//inline 會加速，要不要家都行
//int ans=1 這是默認參數
//放在最後 呼叫時要不要傳入都行
inline int power(int x,const int &y,int ans=1){
  for(int i=1;i<=y;i++,x=x*x%mod) if(i&y) ans=ans*x%mod;
  return ans;
}
signed main(){
  int x,y;
  cin>>x>>y;
  cout<<power(x,y)<<endl;
}

#include<bits/stdc++.h>
#define int long long
using namespace std;
int power(int x, int y){
    if(y==0) return 1;
    if(y==1) return x;
    int tmp=power(x, y/2);
    if(y%2) return tmp*tmp*x;
    else return tmp*tmp;
}
signed main(){
  int x,y;
  cin>>x>>y;
  cout<<power(x,y)<<endl;
}

我比較喜歡這個

謝謝807\(^2\)

分治複雜度怎麼證明啊

數學歸納法 or Master Theorem
不管哪一種都挺複雜ㄉ
講的話可能會燒雞
- ~~而且講師也不熟~~
可以看這份簡報
~~所以我們可以相信複雜度會是好的(誤~~

但剛剛快速冪複雜度蠻直覺ㄉ
每次算完的都會至少變兩倍
\(O(log N)\)
超快ㄉ
如果你跟log不熟 \(log_2 10^{100} \approx 332\)

{D & C - 3}

雖然我覺得這條講了會燒雞

但他蠻重要ㄉ

平面最近點對

平面上有n個點
求任二點距離之最小值
窮舉 \(O(N^2)\)
- 繼續TLE

繼續分治

分
- 算半個平面
治
- 只剩下2-10個點
合併
- 這個才是重點
- 夏夜講

蒿吐合併

你從遞迴下去的東西知道了兩邊的最近點對
- 設其較小值為 k
所以你知道不用看距離線 x 座標大於 k 的人

K

剩下一個小區間ㄌ

這區間怎麼算
對於每個點要找他y座標往上k的點
- 為了避免算到重複的不要同時往上往下
可以被證明最多只要看五個就會看到了
- 先對 y 軸排序

K

為什麼最多只會有五個

因為左右最近距離是 k
所以每個點附近半徑為k的圓不會有東西
除掉原本那個
最多只能塞下五個ㄌ

K

題單

NEOJ
- 124 125 789 795
- 127 128
TIOJ
- 1080

{two pointers}

聽說去年一三沒講雙指針

就是兩根指針

有哪些
- 快慢指針
- 正反指針
- 或就只是指向兩個不同陣列的指針
- 或是很多種不同的應用因為雙指針是屬於一個較雜的技巧
這邊說 雙指針 通常不用存pointer
對指標不熟沒關係存你查到陣列的哪個index就行ㄌ

因為雙指針沒有既定的算法
這邊講幾個例子感受一下雙指針是啥

給點🌰

4533 . B2. 姜姜不想驗b7 (Seven)
- ~~這我們上機考 AC 就打贏80%的人了~~
- 給你一個長度為 \(N\) 的陣列求共有幾個連續區間和小於 \(K\)
- 元素為正整數
- 窮舉所有區間算區間和
  - 上禮拜才剛講
  - 複雜度 \(O(N^2)\) 炸裂
- 思考一下
  - 怎麼從一個區間算其他區間能不能用?
  - 解答在下一頁

雙指針la

假設我們有 \([l, r]\) 這個區間
- 意思是從 \( l, l+1, l+2, ... , r-1, r\)
- 如果\(sum([l, r])<k\)
- 是不是代表 \([l+1, r], [l+2, r], ... , [r-1, r]\) 皆小於k
  - 因為元素是正整數更少元素的陣列之合一定更小
所以我們就能開始算ㄌ
- 對於一個右界 \(r\) 我們找到他最小的左界 \(l\) 使\(sum([l, r])<k\)
- 然後把答案加上\(r-l+1\)就行了
- 怎麼找左右界?
- 雙指針!

這題是快慢指針喔

快指針一次走一步
代表每個右界都會被算到
那慢指針要幹嘛?
維護總和 \(\le k\) 的區間

每次快指針往右走一步會加上他走上的那一格
如果總和 \(\le k\) 就把左界往右移
並減掉原本他在的那格的值

維護好最大的總和 \(\le k\) 的區間後
就知道右界為 x 的區間能製造多少種可能了
加上去並算每個右界的答案數

AC CODE

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
    ios_base::sync_with_stdio(false);cin.tie(0);
    int n, m;cin>>n>>m;
    vector<int> li(n);
    for(int i=0; i<n; i++) cin>>li[i];
    int tot=li[0];
    int fast=0, slow=0;// 我就是快慢指針
    int cnt=0;
    while(fast!=n){
        while(tot>m){
            tot-=li[slow];slow++;
        }
        cnt+=fast-slow+1;
        fast++;
        tot+=li[fast];
    }
    cout<<cnt;
}

基礎演算法們 aka 東西一堆

\(INDEX\)

這我

題外話

題外話 - 2

{enumeration}

枚舉誰不會

沒事

一顆常見的🌰

how to do

🌰的🌰

位元枚舉

位元運算好噁心

遞迴枚舉

{enum-pruning}

決策樹

再講一下枚舉是甚麼

很煩的🌰

既然都是枚舉了 就暴搜吧

🌰的程式🌰

觀察 - 0

觀察 - 1

觀察 - 2

小提醒

題單的啦

{greedy}

一個不用思考的🌰

how to greedy

再看決策樹

¿SO?

來看個真正的greedy🌰

證明啊

AC CODE

{greedy-2}

🌰 - 2

耗

樹

樹

樹

樹

樹

證明？

證明

AC CODE

{greedy-3}

最大線段覆蓋

題單

{binary search}

繼續從🌰講起

二分搜

看動畫

看動畫

看動畫

看動畫

有什麼性質？

有什麼性質？

單調性

單調性

實作

左閉右閉 左閉右開

聽幾次二分搜他就出現幾次

{\(_2\)-search-2}

對答案二分搜

貼海報

什麼東西有單調性

放個示意圖

畈叩

Another 🌰

繼續對答案二分搜

畈叩

思考一下

題單

{divide & conquer}

分治

兩個排好的半個陣列

兩個排好的半個陣列

兩個排好的半個陣列

兩個排好的半個陣列

兩個排好的半個陣列

兩個排好的半個陣列

基礎演算法們
aka 東西一堆

既然都是枚舉了就暴搜吧

左閉右閉左閉右開