資料結構
建國中學 王民人
講師簡介
學歷:延平 → 建中
常用Handle:Astrayt
Discord:Astrayt#6587
想學資結所以來講資結
- 這裡的區間都是左閉右閉
- 編號都是1-based
- 請不要中毒
- 如果我燒雞了請原諒我QQ
小約定
Table of contents
靜態的RMQ
1
Sparse Table
瘦一點的線段樹
2
Fenwick Tree
一切毒瘤的起源
3
Segment Tree
教的東西應該都不陌生,應該蠻簡單的
Sparse Table
稀疏表
例題
給定一個長度為 \(N\) 的正整數序列 \( a_1, ... , a_N\),接著有 \(Q\) 筆詢問,每個詢問可能是下列形式的其中一個:
- \(1\space l \space r\),請你回答 \( max(a_l,...,a_r) \)
- \(2\space l \space r\),請你回答 \( min(a_l,...,a_r) \)
\(N, Q \leq 5 \times 10^5\)
Sparse Table建表
用倍增法存資料的資料結構,下面是取min的Sparse Table:
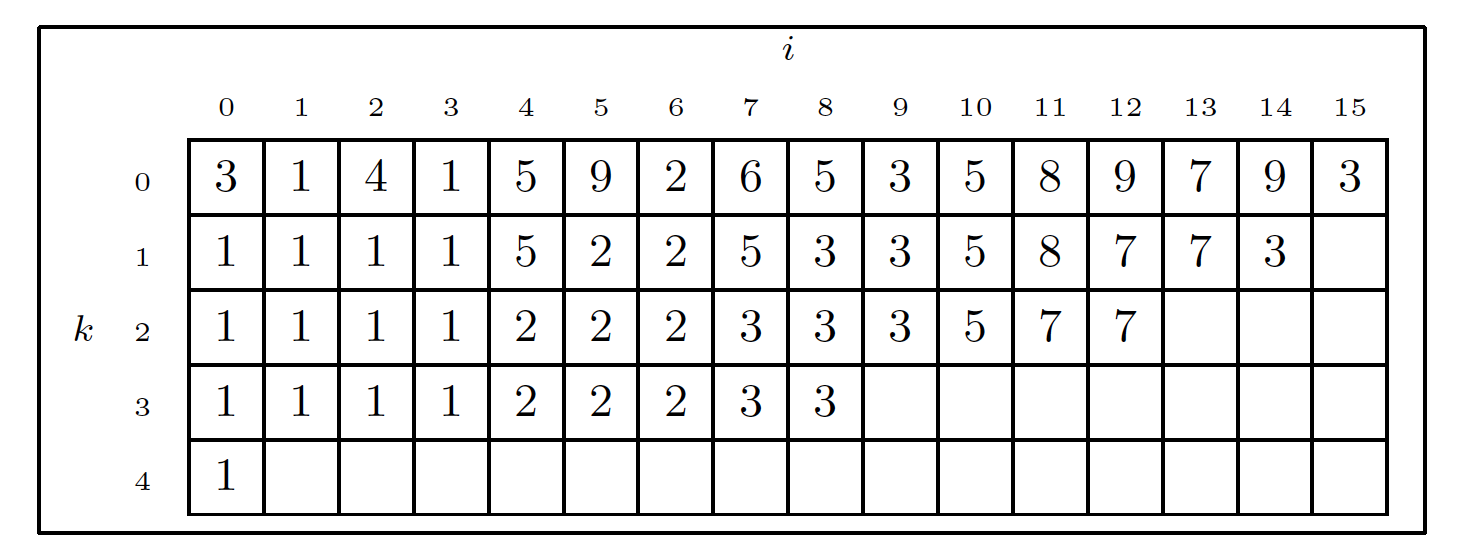
建表時間&空間複雜度 \(O(NlogN)\)
Sparse Table查詢
查詢的時候找到最大的 \(k\) 滿足 \(2^{k} \leq (r - l + 1)\)
就可以在Sparse Table上查詢\(ST[l][k]\)和\(ST[r-2^k+1][k]\)的答案
時間複雜度\(O(1)\)
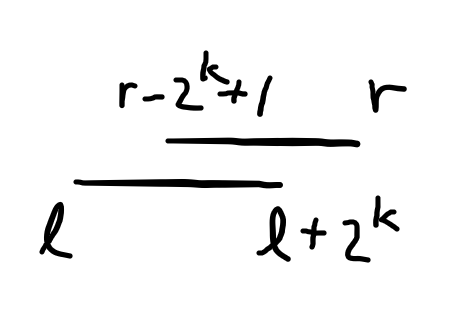
實作
這裡就只實作取min的
反正是一樣的東西
#include <bits/stdc++.h>
using namespace std;
#define starburst ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int a[500005] ,ST[500005][25];
signed main(){
starburst
int n; cin >> n;
int q; cin >> q;
for(int i = 1; i <= n; ++i){
cin >> a[i];
ST[i][0] = a[i];
}
for(int j = 1; (1<<j) <= n; ++j){
for(int i = 1; i + (1 << j) - 1 <= n; ++i){
ST[i][j] = min(ST[i][j - 1], ST[i + (1 << (j - 1))][j - 1]);
}
}
for(; q; q--){
int l, r; cin >> l >> r;
int k = 0;
while((1 << (k + 1)) <= (r - l + 1)) k++;
cout << min(ST[l][k], ST[r - (1<<k) + 1][k]) << '\n';
}
}
使用時的注意事項
有些東西不太適合砸Sparse Table
像是區間Sum、區間最大連續和等問題
但也有適合用Sparse Table的時候
畢竟查詢只要\(O(1)\)
請各位自行注意使用時機
滾動Sparse Table
如果你有注意到的話,其實Sparse Table和DP一樣可以滾動
但會變離線詢問
只要把詢問依照區間長度排序
就可以從用滾動的方法建立表格並回答所有詢問即可
想試的話請自己實作
因為講師不想做
Fenwick Tree
樹狀數組
a.k.a. Binary Indexed Tree
a.k.a. BIT
BIT的結構
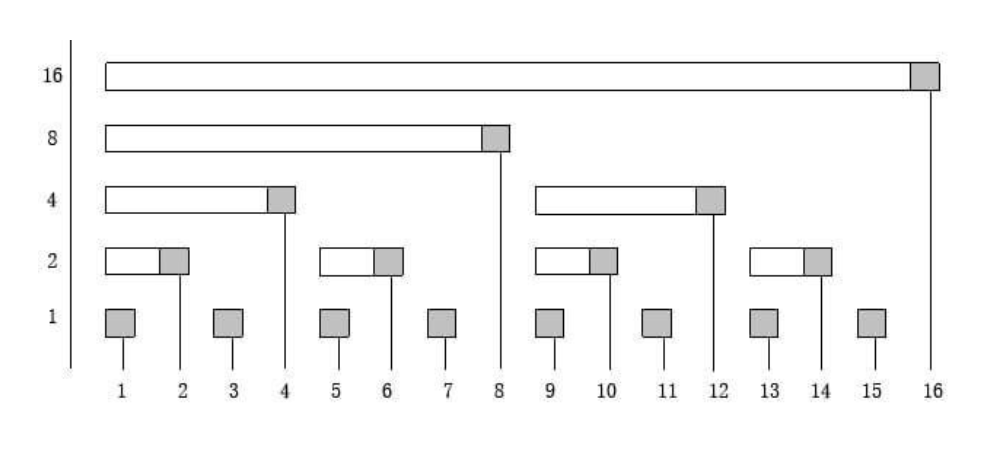
可以做什麼?
在\(O(logN)\)的時間維護前後綴
(操作要有結合律喔)
實作
struct FenwickTree{
int val[maxn];
void upd(int p, int v){
for(; p < N; p += (p & -p)) val[p] += v;
}
int qry(int p){
int ret = 0;
for(; p; p -= (p&-p)) ret += val[p];
return ret;
}
}bit;BIT的能耐
BIT的用處相當廣
通常題目困難的地方不會是實作
而是如何抓到方法利用這個工具
由於以下題目的操作大同小異
所以不會附Code
BIT Lv. 1
給定一個長度為 \(N\) 的正整數序列 \( a_1, ... , a_N\),接著有 \(Q\) 筆操作,每個操作可能是下列形式的其中一個:
- \(1\space k\) 請你回答 \(a_k\) 的值
- \(2\space l \space r \space x\) 對所有 \(i \in [l,r]\),\(a_i += x\)
\(N, Q \leq 2 \times 10^5\)
BIT Lv. 2
給定一個長度為 \(N\) 的正整數序列 \( a_1, ... , a_N\),請你回答總共有幾對 \((i, j)\) 滿足 \(a_i > a_j\) 且 \(i < j\)。
\(N \leq 2 \times 10^5\)
BIT Lv. 3
給定一個長度為 \(N\) 的正整數序列 \( a_1, ... , a_N\),請找出最長遞增子序列的長度。
\(N \leq 2 \times 10^5\)
Segment Tree
線段樹
線段樹 Lv. 1
給定一個長度為 \(N\) 的正整數序列 \( a_1, ... , a_N\),接著有 \(Q\) 筆操作,每個操作可能是下列形式的其中一個:
- \(1\space l \space r\),請你回答 \(\sum\limits^{r}_{i=l}a_i\)
- \(2\space p \space x\),把 \(a_p\) 改成 \( x \)
\(N, Q \leq 2 \times 10^5\)
線段樹的結構
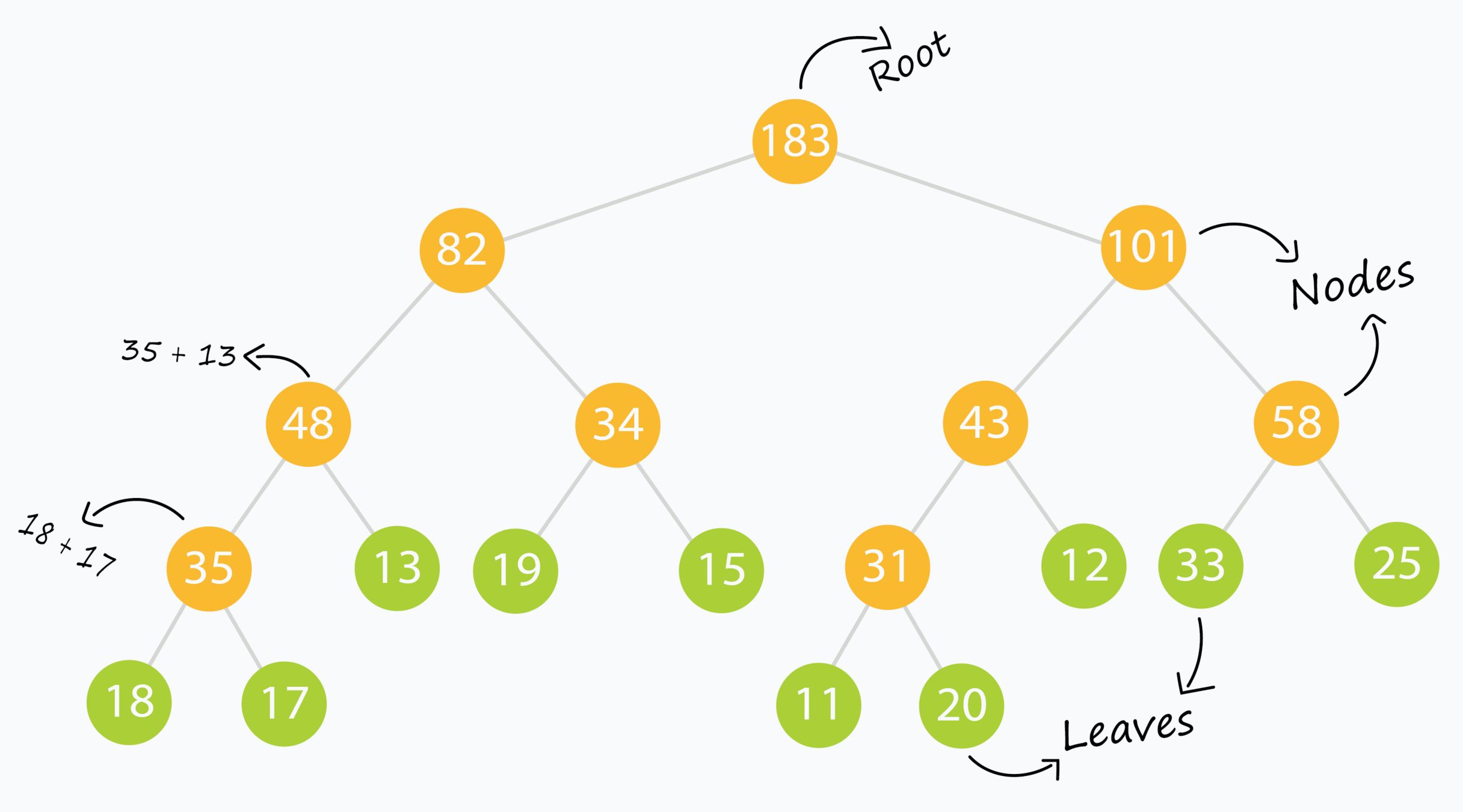
Source: Leetcode
實作
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define starburst ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define maxn 200005
struct SegmentTree{
int node[4*maxn];
void modify(int l, int r, int i, int p, int x){
if(l == r){
node[i] = x;
return;
}
int mid = (l + r) / 2, ls = 2 * i, rs = 2 * i + 1;
if(p <= mid) modify(l, mid, ls, p, x);
else modify(mid + 1, r, rs, p, x);
node[i] = node[ls] + node[rs];
}
int query(int l, int r, int i, int ql, int qr){
if(ql <= l && r <= qr){
return node[i];
}
int ret = 0, mid = (l + r) / 2, ls = 2 * i, rs = 2 * i + 1;
if(ql <= mid) ret += query(l, mid, ls, ql, qr);
if(mid < qr) ret += query(mid + 1, r, rs, ql, qr);
return ret;
}
}seg;
void solve(){
int n, q; cin >> n >> q;
for(int i = 1; i <= n; ++i){
int ai; cin >> ai;
seg.modify(1, n, 1, i, ai);
}
for(; q; q--){
int op; cin >> op;
if(op == 1){
int l, r; cin >> l >> r;
cout << seg.query(1, n, 1, l, r) << '\n';
}else {
int p, x; cin >> p >> x;
seg.modify(1, n, 1, p, x);
}
}
}
signed main(){
starburst
int t = 1; //cin >> t;
while(t--) solve();
}
才不只這樣!
事實上,線段樹能作到的事情遠不只如此
所有具有結合律的操作都可以用線段樹做!
像是區間Xor、區間極值都可以
接下來試試看做區間修改的線段樹
線段樹 Lv. 2
給定一個長度為 \(N\) 的正整數序列 \( a_1, ... , a_N\),接著有 \(Q\) 筆操作,每個操作可能是下列形式的其中一個:
- \(1\space l \space r\),請你回答 \(\sum\limits^{r}_{i=l}a_i\)
- \(2\space l \space r \space x\) 對所有 \(i \in [l,r]\),\(a_i += x\)
\(N, Q \leq 2 \times 10^5\)
懶人標記
對於第一次遇到的人來說可能比較難想到
當我們遇到一個節點,節點的區間都在修改區間內的話
就直接改那個節點,打上標記
要碰子節點的時候將標記下推即可
等等畫圖解釋>.<
實作
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define starburst ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define maxn 200005
#define ls (2*i)
#define rs (2*i+1)
#define mid ((l+r)/2)
struct SegmentTree{
int node[4*maxn], tag[4*maxn];
void push(int l, int r, int i){
int t = tag[i]; tag[i] = 0;
node[ls] += (mid - l + 1) * t, tag[ls] += t;
node[rs] += (r - mid) * t, tag[rs] += t;
node[i] = node[ls] + node[rs];
}
void modify(int l, int r, int i, int ql, int qr, int x){
if(ql <= l && r <= qr){
node[i] += (r - l + 1) * x;
tag[i] += x;
return;
}
push(l, r, i);
int mid = (l + r) / 2, ls = 2 * i, rs = 2 * i + 1;
if(ql <= mid) modify(l, mid, ls, p, x);
if(mid < qr) modify(mid + 1, r, rs, p, x);
node[i] = node[ls] + node[rs];
}
int query(int l, int r, int i, int ql, int qr){
if(ql <= l && r <= qr){
return node[i];
}
push(l, r, i);
int ret = 0, mid = (l + r) / 2, ls = 2 * i, rs = 2 * i + 1;
if(ql <= mid) ret += query(l, mid, ls, ql, qr);
if(mid < qr) ret += query(mid + 1, r, rs, ql, qr);
return ret;
}
}seg;
void solve(){
int n, q; cin >> n >> q;
for(int i = 1; i <= n; ++i){
int ai; cin >> ai;
seg.modify(1, n, 1, i, i, ai);
}
for(; q; q--){
int op; cin >> op;
if(op == 1){
int l, r; cin >> l >> r;
cout << seg.query(1, n, 1, l, r) << '\n';
}else {
int l, r, x; cin >> l >> r >> x;
seg.modify(1, n, 1, l, r, x);
}
}
}
signed main(){
starburst
int t = 1; //cin >> t;
while(t--) solve();
}
線段樹 Lv. 3
給定一個長度為 \(N\) 的正整數序列 \( a_1, ... , a_N\),接著有 \(Q\) 筆操作,操作為以下形式:
- \(p \space x\),把 \(a_p\) 改成 \( x \)
請在每筆操作後輸出最大子區間和
\(N, Q \leq 2 \times 10^5\)
特殊的節點
我們不難發現,這題節點只存一個整數做不了事情
不妨考慮存四個資訊:最大前綴、最大後綴、最大子區間和、區間和
從這裡可以知道,其實線段樹的節點存的可以是任何東西
你甚至可以在線段樹內套一棵線段樹
這樣就可以做到二維的區間修改/查詢
實作
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define int ll
#define starburst ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define maxn 200005
#define mid ((l+r)/2)
#define ls (2*i)
#define rs (ls+1)
struct SegmentTree{
struct Node{
int pre, suf, sum, mx;
}node[maxn * 4];
void update(int x, int i){
node[i].pre = node[i].suf = node[i].sum = node[i].mx = x;
}
void pull(Node &cur, Node L, Node R){
cur.pre = max(L.pre, L.sum + R.pre);
cur.suf = max(R.suf, R.sum + L.suf);
cur.sum = L.sum + R.sum;
cur.mx = max(max(L.mx, R.mx), L.suf + R.pre);
}
void modify(int l, int r, int i, int p, int x){
if(l == r){
update(x, i);
return;
}
if(p <= mid) modify(l, mid, ls, p, x);
else modify(mid + 1, r, rs, p, x);
pull(node[i], node[ls], node[rs]);
}
}seg;
void solve(){
int n, q; cin >> n >> q;
for(int i = 1; i <= n; ++i) {
int x; cin >> x;
seg.modify(1, n, 1, i, x);
}
for(; q; q--){
int k, x; cin >> k >> x;
seg.modify(1, n, 1, k, x);
cout << max(0ll, seg.node[1].mx) << '\n';
}
}
signed main(){
starburst
int t = 1; //cin >> t;
while(t--) solve();
}
線段樹 Lv. 4
應用:DP優化
列出DP式:\( DP[i] = \max_{h[j] < h[i]}\{DP[j] + a_i\}\)
看起來轉移要\(O(N)\)
我們發現可以對\(h\)的值域開線段樹
這樣就可以達到\(O(logN)\)查詢最大值
成功把時間壓下來了
實作
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define int ll
#define starburst ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define maxn 200005
#define ls (2 * i)
#define rs (2 * i + 1)
#define mid ((l + r) / 2)
struct SegmentTree{
int val[maxn * 4];
void modify(int l, int r, int i, int p, int x){
if(l == r){
val[i] = x;
return;
}
if(p <= mid) modify(l, mid, ls, p, x);
else modify(mid + 1, r, rs, p, x);
val[i] = max(val[ls], val[rs]);
}
int query(int l, int r, int i, int ql, int qr){
if(ql <= l && r <= qr){
return val[i];
}
int ret = 0;
if(ql <= mid) ret = max(ret, query(l, mid, ls, ql, qr));
if(mid < qr) ret = max(ret, query(mid + 1, r, rs, ql, qr));
return ret;
}
}seg;
void solve(){
int n; cin >> n;
vector<int> dp(n, 0), h(n, 0), a(n, 0);
for(auto &x:h) cin >> x;
for(auto &x:a) cin >> x;
for(int i = 0; i < n; ++i){
dp[i] = (h[i] == 1 ? 0 : seg.query(1, n, 1, 1, h[i] - 1)) + a[i];
seg.modify(1, n, 1, h[i], dp[i]);
}
cout << *max_element(dp.begin(), dp.end());
}
signed main(){
starburst
int t = 1; //cin >> t;
while(t--) solve();
}
其他有關線段樹的技巧:
掃描線
二維線段樹
動態開點
持久化線段樹
戰鬥線段樹
李超線段樹
時間線段樹
線段樹優化建圖
Pattern
吉如一線段樹(Segment Tree Beats)
但題目裡可能會出現,可以等學會了再寫
有興趣可以先上網學
開始寫題目囉
➡️
等等會抓幾題講解