Python 資料分析
講師：乘一、溫室蔡
NumPy & Matplotlib
何謂資料分析
從資料中「看出什麼」的過程
可分為三個步驟：
一、資料獲取
二、資料處理
三、資料視覺化
EX：爬蟲
EX：多項式擬合
EX：折線圖
萬能的 Python
這些東西在 Python 都有專門的套件處理
而 NumPy 與 Matplotlib
就分別對應到處理與視覺化的部分
- Python 標配
- 陣列、矩陣運算
- 方便的數學函式
- 以C語言撰寫，高效能
談談線性代數
\begin{bmatrix}
3 \\
4
\end{bmatrix}
談談線性代數
\begin{bmatrix}
3 \\
4
\end{bmatrix}
3
4
0
向量：
自原點向外延伸的箭頭
以其在各軸上的分量表示
y
x
談談線性代數
\begin{bmatrix}
3 \\
4
\end{bmatrix}
3
4
0
純量乘法：
箭頭沿線縮放
分量逐項相乘
y
x
=
\begin{bmatrix}
1.5 \\
2
\end{bmatrix}
1.5
2
\frac{1}{2}
談談線性代數
\begin{bmatrix}
3 \\
4
\end{bmatrix}
3
4
0
向量加法：
箭頭頭尾相接
分量逐項相加
y
x
\begin{bmatrix}
2 \\
-1
\end{bmatrix}
+
=
\begin{bmatrix}
5 \\
3
\end{bmatrix}
3
5
談談線性代數
\begin{bmatrix}
3 \\
4
\end{bmatrix}
3
4
0
向量減法：
箭頭頭頂相連
分量逐項相減
y
x
\begin{bmatrix}
2 \\
-1
\end{bmatrix}
-
=
\begin{bmatrix}
5 \\
3
\end{bmatrix}
3
5
談談線性代數
\begin{bmatrix}
3 \\
4
\end{bmatrix}
向量內積／點積：
逐項相乘後各項總和
\cdot
=
\begin{bmatrix}
5 \\
3
\end{bmatrix}
5\times3
3\times4
+
=
27
談談線性代數
矩陣：
有 列（rows） 行（columns）的矩陣
圖為 矩陣
\begin{bmatrix}
1 & 4 \\
2 & 5 \\
3 & 6
\end{bmatrix}
m \times n
m
n
3 \times 2
談談線性代數
矩陣的幾何意義：
與向量相乘，以對該向量進行特定的空間變換
如旋轉矩陣：
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta \\
\end{bmatrix}
y
x
\theta
談談線性代數
矩陣乘法：
兩矩陣 的維度分別為 與
則相乘後得到矩陣 維度為
且第 列第 項
m \times n
n \times p
m \times p
i
j
\mathbf{AB}
\mathbf{A},\mathbf{B}
(\mathbf{AB})_{i,j}=\displaystyle\sum_{r=1}^{n}a_{i,r}b_{r,j}
談談線性代數
\begin{bmatrix}
6&-7\\
1&3\\
-2&9
\end{bmatrix}
\begin{bmatrix}
7&6&-8&5\\
4&-5&2&-9
\end{bmatrix}
談談線性代數
\begin{bmatrix}
6&-7\\
1&3\\
-2&9
\end{bmatrix}
\begin{bmatrix}
7&6&-8&5\\
4&-5&2&-9
\end{bmatrix}
\begin{bmatrix}
14&71&-62&93\\
19&-9&-2&-22\\
22&-57&34&-91
\end{bmatrix}
42
-28
談談線性代數
\begin{bmatrix}
6&-7\\
1&3\\
-2&9
\end{bmatrix}
\begin{bmatrix}
7&6&-8&5\\
4&-5&2&-9
\end{bmatrix}
\begin{bmatrix}
14&71&-62&93\\
19&-9&-2&-22\\
22&-57&34&-91
\end{bmatrix}
42
-28
談談線性代數
\begin{bmatrix}
6&-7\\
1&3\\
-2&9
\end{bmatrix}
\begin{bmatrix}
7&6&-8&5\\
4&-5&2&-9
\end{bmatrix}
\begin{bmatrix}
14&71&-62&93\\
19&-9&-2&-22\\
22&-57&34&-91
\end{bmatrix}
6
-8
談談線性代數
\begin{bmatrix}
6&-7\\
1&3\\
-2&9
\end{bmatrix}
\begin{bmatrix}
7&6&-8&5\\
4&-5&2&-9
\end{bmatrix}
\begin{bmatrix}
14&71&-62&93\\
19&-9&-2&-22\\
22&-57&34&-91
\end{bmatrix}
-8
6
談談線性代數
\begin{bmatrix}
6&-7\\
1&3\\
-2&9
\end{bmatrix}
\begin{bmatrix}
7&6&-8&5\\
4&-5&2&-9
\end{bmatrix}
\begin{bmatrix}
14&71&-62&93\\
19&-9&-2&-22\\
22&-57&34&-91
\end{bmatrix}
NumPy 實際應用
NumPy 非內建套件
可以在終端機使用 pip 安裝：
$ pip install numpy在 Python 中如下引入：
import numpy as npNumPy 的核心：多維陣列
陣列就是裝了多個元素的東西
a = np.array([1, 2, 3])
print(a) # [1 2 3]
b = np.array([[1, 2], [3, 4], [5, 6]])
print(b)
# [[1 2]
# [3 4]
# [5 6]]如果陣列裡面裝陣列，那就是二維陣列
陣列裡面的陣列裝陣列，那就是三維陣列
NumPy 的核心：多維陣列
ndarray (n-dimensional array)
a = np.array([[1, 2], [3, 4], [5, 6]])
# 幾乘幾的陣列
print(a.shape) # (3, 2)
# 幾維的陣列
print(a.ndim) # 2
# 裝什麼型別
print(a.dtype) # dtype('int64')可由 np.array() 轉換 Python 陣列而來
其有一些重要的屬性：
多維陣列索引
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])\begin{bmatrix}
1&2&3\\
4&5&6\\
7&8&9
\end{bmatrix}
0
1
2
0
1
2
多維陣列索引
print(a[0]) # [1 2 3]\begin{bmatrix}
1&2&3\\
4&5&6\\
7&8&9
\end{bmatrix}
0
1
2
0
1
2
多維陣列索引
print(a[0, 2]) # 3\begin{bmatrix}
1&2&3\\
4&5&6\\
7&8&9
\end{bmatrix}
0
1
2
0
1
2
多維陣列索引
print(a[1:]) # [[4 5 6]
# [7 8 9]]\begin{bmatrix}
1&2&3\\
4&5&6\\
7&8&9
\end{bmatrix}
0
1
2
0
1
2
多維陣列索引
print(a[:, 1]) # [2 5 8]\begin{bmatrix}
1&2&3\\
4&5&6\\
7&8&9
\end{bmatrix}
0
1
2
0
1
2
多維陣列索引
print(a[[0, 2], [0, 2]]) # [1 9]\begin{bmatrix}
1&2&3\\
4&5&6\\
7&8&9
\end{bmatrix}
0
1
2
0
1
2
多維陣列方法
a = np.array([1, 2, 3, 4, 5, 6])
# 轉換成 3x2 矩陣
print(a.reshape(3, 2))
# [[1 2]
# [3 4]
# [5 6]]
# 轉換型別
print(a.astype(float))
# [[1. 2.]
# [3. 4.]
# [5. 6.]]
# 矩陣轉置
print(a.T)
# [[1 3 5]
# [2 4 6]]ndarray 有一些常用的方法：
要注意的是這些方法
都不會修改原來的陣列
而是回傳修改後的陣列
NumPy 四則運算
a = np.array([6, 8, 2])
b = np.array([1, 9, 4])
# 加法
print(a + b) # [7 17 6]
# 減法
print(a - b) # [5 -1 -2]
# 純量加減法
print(a + 5) # [11 13 7]
# 純量乘法
print(2 * a) # [12 16 4]
# 逐項乘法（非向量內稽！）
print(a * b) # [6 72 8]
# 內積
print(np.dot(a, b)) # 86
花式建陣列
# 從 Python 陣列建立
print(np.array([4, 3, 9])) # [4 3 9]
# 建立全為 0 的陣列
print(np.zeros(5)) # [0. 0. 0. 0. 0.]
# 3x2 零陣列
print(np.zeros((3, 2)))
# [[0 0]
# [0 0]
# [0 0]]
# 建立全為 1 的陣列
print(np.ones(4)) # [1. 1. 1. 1.]
# 用類似 range() 的方法建矩陣
print(np.arange(1, 10, 2)) # [1 3 5 7 9]
# 在範圍內產生平均分布的 n 個點
print(np.linspace(2.0, 3.0, 20))
# [2. 2.05263158 2.10526316 2.15789474 2.21052632 2.26315789
# 2.31578947 2.36842105 2.42105263 2.47368421 2.52631579 2.57894737
# 2.63157895 2.68421053 2.73684211 2.78947368 2.84210526 2.89473684
# 2.94736842 3. ]
# 生成隨機陣列
np.random.rand(2, 5) # 2x5, [0, 1) 平均分布
np.random.randn(4, 3) # 4x3, 標準常態分布
np.random.randint(1, 10, size=(5, 3)) # 5x3, [1, 10) 整數平均分布NumPy 的龐大函式庫
a = np.arange(5)
print(a) # [0 1 2 3 4]
# 三角函數
print(np.sin(a)) # [ 0. 0.84147098 0.90929743 0.14112001 -0.7568025 ]
print(np.cos(a)) # [ 1. 0.54030231 -0.41614684 -0.9899925 -0.65364362]
print(np.tan(a)) # [ 0. 1.55740772 -2.18503986 -0.14254654 1.15782128]
# 次方
print(np.power(a, 2)) # [ 0 1 4 9 16]
# 平方根
print(np.sqrt(a)) # [0. 1. 1.41421356 1.73205081 2. ]
# 自然對數
print(np.log(a)) # [ -inf 0. 0.69314718 1.09861229 1.38629436]
# 最大最小值
print(np.max(a)) # 4
print(np.min(a)) # 0
# ...NumPy 內建了大量的數學函式
大部分都是「逐項套用」
Vectorizing functions
def relu(x):
return x if x > 0 else 0
vrelu = np.vectorize(relu)
a = np.random.randn(5)
print(a)
# [ 0.86929017 -0.42837333 2.03339915 0.27163138 -0.41706056]
print(vrelu(a))
# [ 0.86929017 0. 2.03339915 0.27163138 0. ]
NumPy 也可以讓你把自己的函式
變成可以「逐項套用」的版本
使用 np.vectorize()
NumPy 是一個非常強大的數學函式庫
但目前為止，我們都只能看到一堆數字
解讀資料時，顯然需要更視覺化的方式
Matplotlib
- 繪製各式圖表
- 與numpy連用
- 建構在MATLAB的基礎上
- 可以製作會動的圖表
Matplotlib 架構
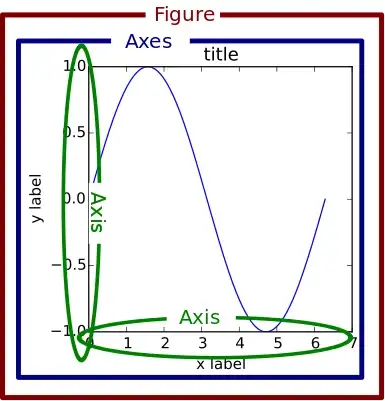
Figure: 空白畫布
axis: 坐標軸
axes: 一套座標軸
subplot: 子圖
Matplotlib 架構
Matplotlib 實際應用
Matplotlib 非內建套件
一樣在終端機使用 pip 安裝：
$ pip install matplotlib在 Python 中如下引入：
import matplotlib.pyplot as plt輸出折線圖
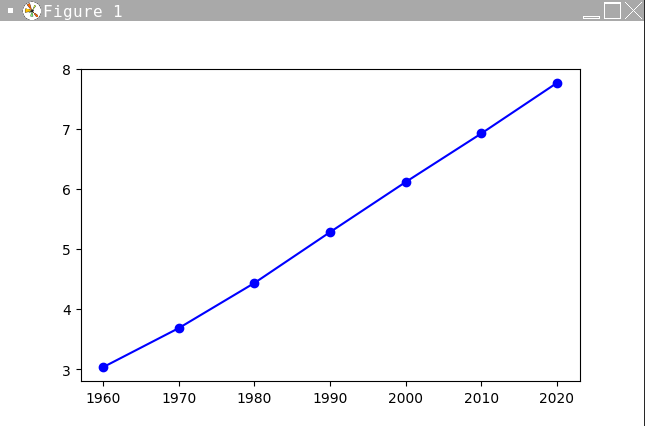
import matplotlib.pyplot as plt
year = [1960, 1970, 1980, 1990, 2000, 2010, 2020]
population = [3.032, 3.682, 4.433, 5.28, 6.114, 6.922, 7.764]
fig = plt.figure() #建立畫布
ax = fig.add_subplot(111) #增加一個子圖
ax.plot(year,population) #畫上x,y軸及資料
plt.show() #輸出折線圖plt.show()
輸出折線圖
plt.plot(x,y,'style-code')
import matplotlib.pyplot as plt
year = [1960, 1970, 1980, 1990, 2000, 2010, 2020]
population = [3.032, 3.682, 4.433, 5.28, 6.114, 6.922, 7.764]
plt.plot(year, population, "b-o") #畫出折線圖
plt.show() #輸出折線圖plt.show()
輸出折線圖
輸出折線圖
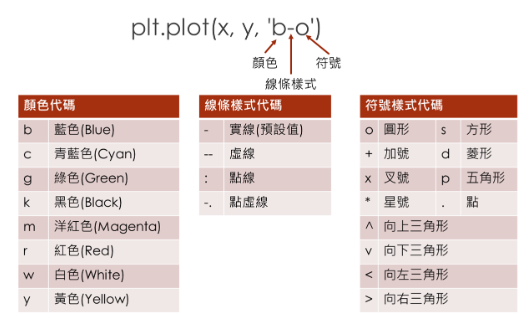
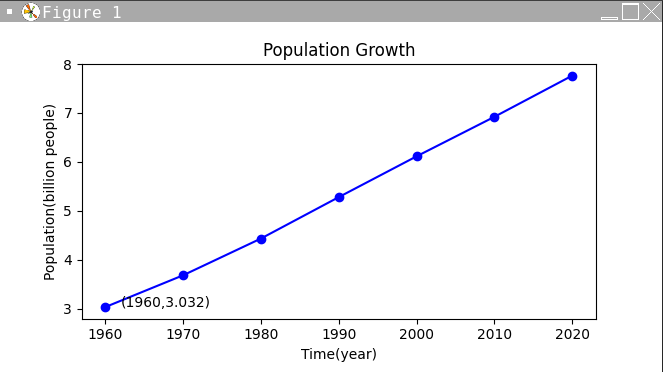
加入文字?
plt.title("string"): 寫入標題
plt.xlabel('string'): x軸標題
plt.ylabel('string'): y軸標題
plt.text(xp, yp, 'string'): 在圖上xp, yp的位置寫字
p的位置寫字
import matplotlib.pyplot as plt
......
......
plt.title("Population Growth")
plt.xlabel("Time(year)")
plt.ylabel("Population(billion people)")
plt.text(1962,3.032,"(1960,3.032)")
plt.show()加入文字?
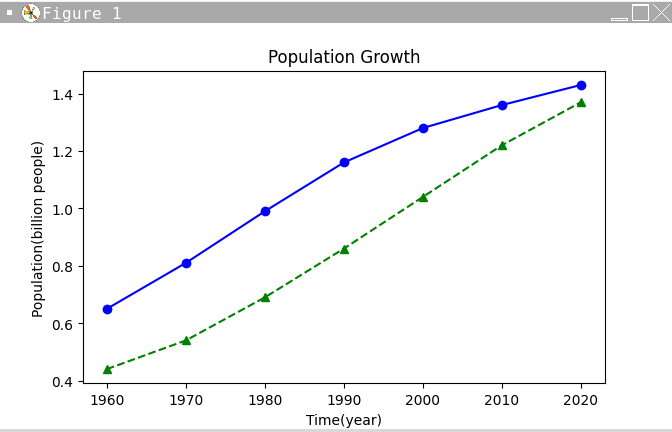
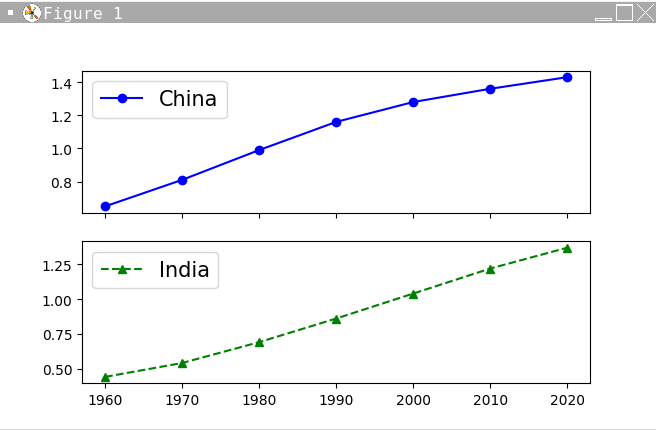
多筆數據?
import matplotlib.pyplot as plt
year = [1960, 1970, 1980, 1990, 2000, 2010, 2020]
y1 = [0.65, 0.81, 0.99, 1.16, 1.28, 1.36, 1.43] #中國人口
y2 = [0.44, 0.54, 0.69, 0.86, 1.04, 1.22, 1.37] #印度人口
plt.plot(year, y1, "b-o", year, y2, "g--^") #畫出折線圖
plt.title("Population Growth")
plt.xlabel("Time(year)")
plt.ylabel("Population(billion people)")
plt.show()多筆數據?
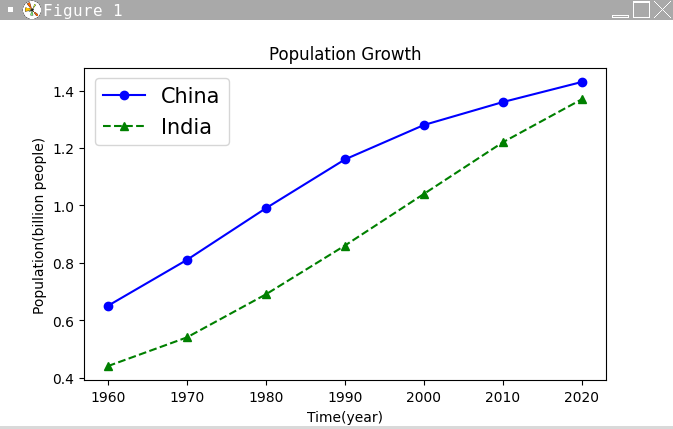
圖示說明?
import matplotlib.pyplot as plt
......
......
plt.legend(["China", "India"], loc="best", fontsize=15) #設定圖例
plt.show()plt.legend([list of legend text],loc='location')
location: 'best'、'upper right'......
更多設定看這裡
圖示說明?
自訂坐標軸
plt.xticks([tick marks],[mark labels]) ：x軸刻度、標記
plt.yticks([tick marks],[mark labels]) ：y軸刻度、標記
plt.xlim([min,max]) : x坐標軸下、上界
plt.ylim([min,max]) : y坐標軸下、上界
自訂坐標軸
import matplotlib.pyplot as plt
#......
#......
plt.xticks([1960,1965,1970,1975,1980,1985,1990,1995,2000,2005,2010,2015,2020])
plt.ylim([0,2])
plt.show()多張圖表
plt.subplots(m,n,sharex='...',sharey='...')
m,n: 垂直、水平方向上有幾張圖
sharex,sharey: 共用x,y軸座標，可填入:
'col': 垂直方向小圖共用
'row': 水平方向小圖共用
'all': 全部小圖共用
'false'(default): 不共用(預設)
在同一個視窗畫出m*n張圖表
多張圖表
在同一個視窗畫出m*n張圖表
import matplotlib.pyplot as plt
year = [1960, 1970, 1980, 1990, 2000, 2010, 2020]
y1 = [0.65, 0.81, 0.99, 1.16, 1.28, 1.36, 1.43]
y2 = [0.44, 0.54, 0.69, 0.86, 1.04, 1.22, 1.37]
fig,ax = plt.subplots(2,1,sharex = "col")
#建立畫布(fig)及劃分2*1個子圖，垂直方向共用x座標軸
ax[0].plot(year, y1, "b-o") #在左上數到右下第0個(但他只有一維)
ax[1].plot(year, y2, "g--^") #畫出折線圖
ax[0].legend(["China"], loc="best", fontsize=15)
ax[1].legend(["India"], loc="best", fontsize=15)
plt.show()多張圖表
換個方法?
import matplotlib.pyplot as plt
year = [1960, 1970, 1980, 1990, 2000, 2010, 2020]
y1 = [0.65, 0.81, 0.99, 1.16, 1.28, 1.36, 1.43]
y2 = [0.44, 0.54, 0.69, 0.86, 1.04, 1.22, 1.37]
ax1 = plt.subplot(211)
ax2 = plt.subplot(212)
ax1.plot(year, y1, "b-o")
ax2.plot(year, y2, "g--^") #畫出折線圖
ax1.legend(["China"], loc="best", fontsize=15)
ax2.legend(["India"], loc="best", fontsize=15)
plt.show()plt.subplot(m,n,i) m*n圖表中的第i個
多張圖表
在同一個視窗畫出m*n張圖表
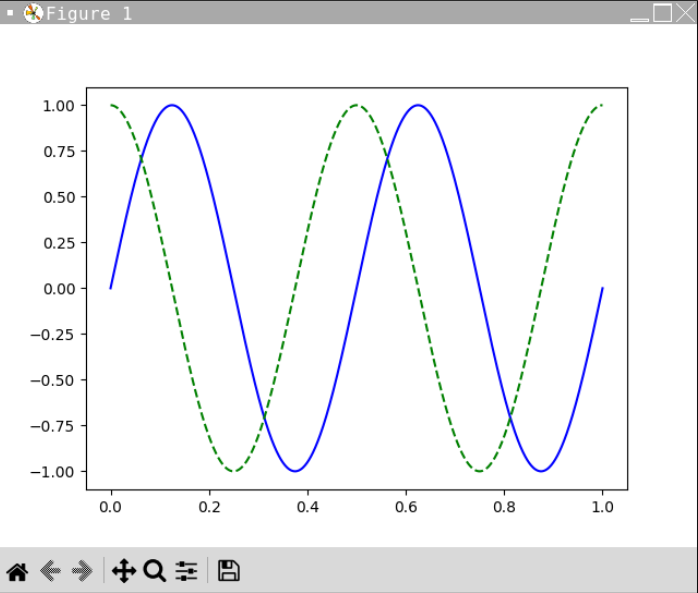
與numpy連用
創建sin圖形與cos圖形
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0,1.0,1000)
#創建一個從0到1，共1000個平均分布元素的陣列
y1 = np.sin(4*np.pi*x)
y2 = np.cos(4*np.pi*x)
plt.plot(x,y1,"b-",x,y2,"g--")
plt.show()
與numpy連用
創建sin圖形與cos圖形
我想讓圖表動起來...
plt.ion() : 打開互動模式，圖表才會更新
set_data(x, y) : 更新x, y資料
fig.canvas.draw() : 重新繪圖
fig.canvas.flush_events() : 輸出新圖表
我想讓圖表動起來...
import matplotlib.pyplot as plt
import numpy as np
plt.ion()
x = np.linspace(0,1.0,1000)
#創建一個從0到1，共1000個平均分布元素的陣列
y = np.sin(4*np.pi*x)
fig,ax = plt.subplots() #建立畫布
pic, = ax.plot(x,y,'b-')
i=0
while True:
i+=0.01
ux = np.linspace(0,1.0,1000)+i
uy = np.sin(4*np.pi*ux)
pic.set_data(x,uy) #重新設定x,y資料
fig.canvas.draw() #重新繪圖
fig.canvas.flush_events()我想讓圖表動起來...
實際演練!
讓矩陣旋轉起來吧!
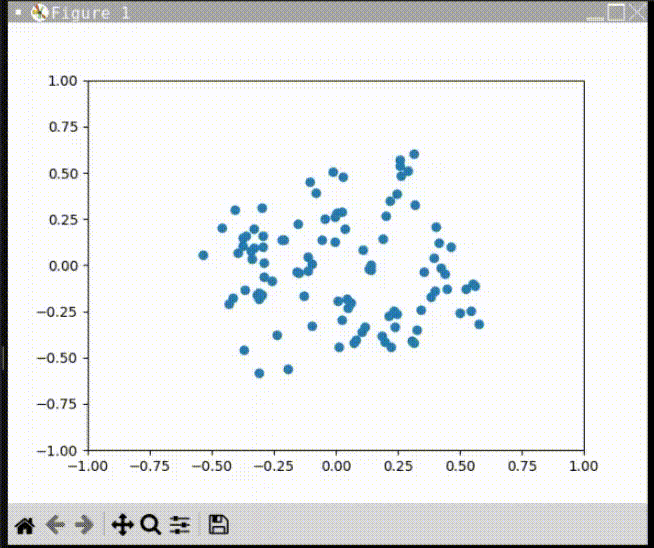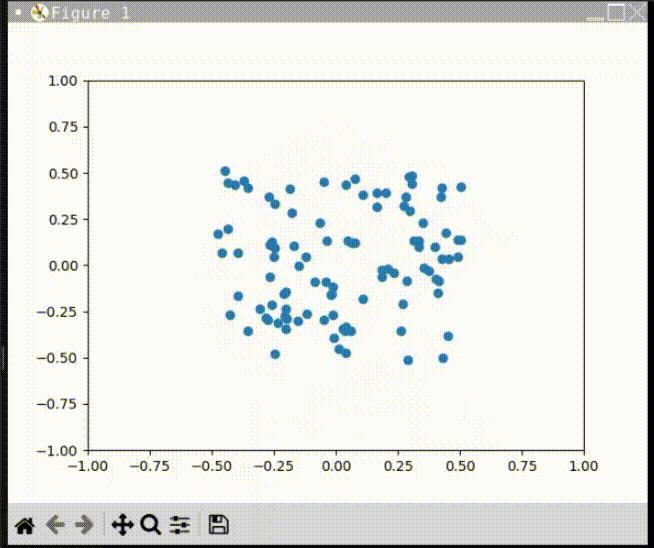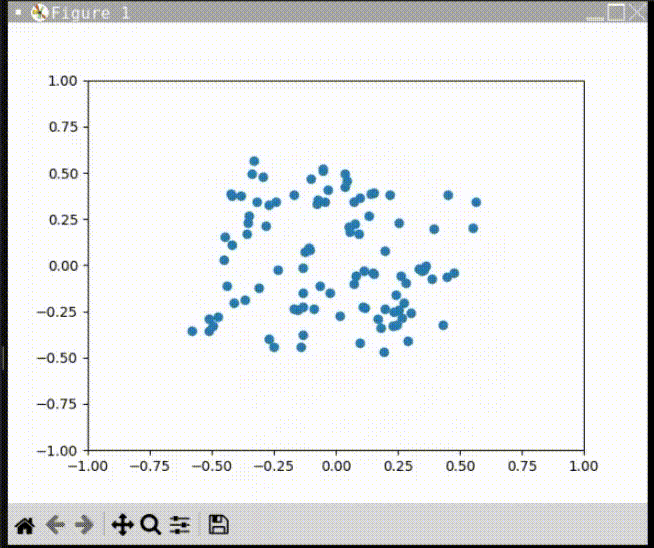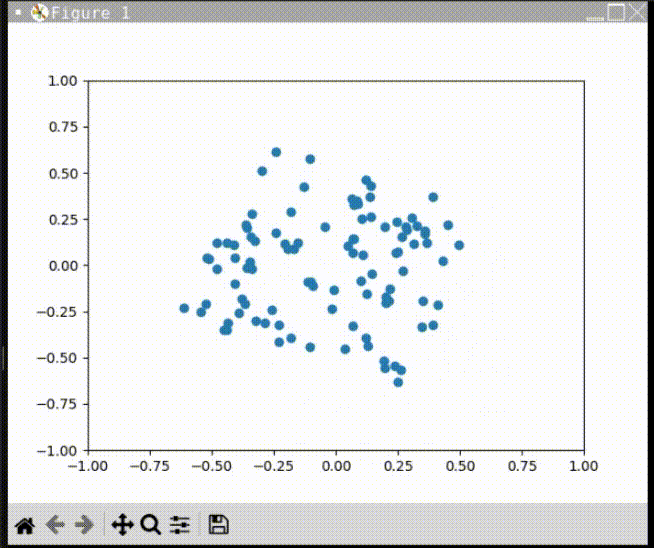
實際演練!
讓矩陣旋轉起來吧!
import numpy as np
import matplotlib.pyplot as plt
def rotate(vectors, theta):
rotmat = np.array([
[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]
])
return np.dot(rotmat, vectors)
if __name__ == '__main__':
npoints = 100
points = np.random.rand(2, npoints)-0.5
plt.ion()
fig, ax = plt.subplots()
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
markers, = ax.plot(points[0], points[1], 'o')
while True:
points = rotate(points, 0.1)
markers.set_data(points[0], points[1])
fig.canvas.draw()
fig.canvas.flush_events()The end!
