深度學習

講師：溫室蔡

機器學習[3]

圖像辨識

在上一次的課程當中

我們訓練了一個多層感知器

來辨識手寫數字資料集 MNIST

這就是「圖像辨識」的一種

但是有個問題…

效率低下

使用多層感知器辨識圖片

我們單純地將圖片中的每個像素攤平

作為神經網路的輸入

然而從資訊論的角度來看

許多的資料是瑣碎的

特徵擷取

以人類的視覺為例

當我們在辨識物體時

我們會先辨識出部分特徵

再由這些特徵去辨識整體圖像

卷積神經網路（CNN）

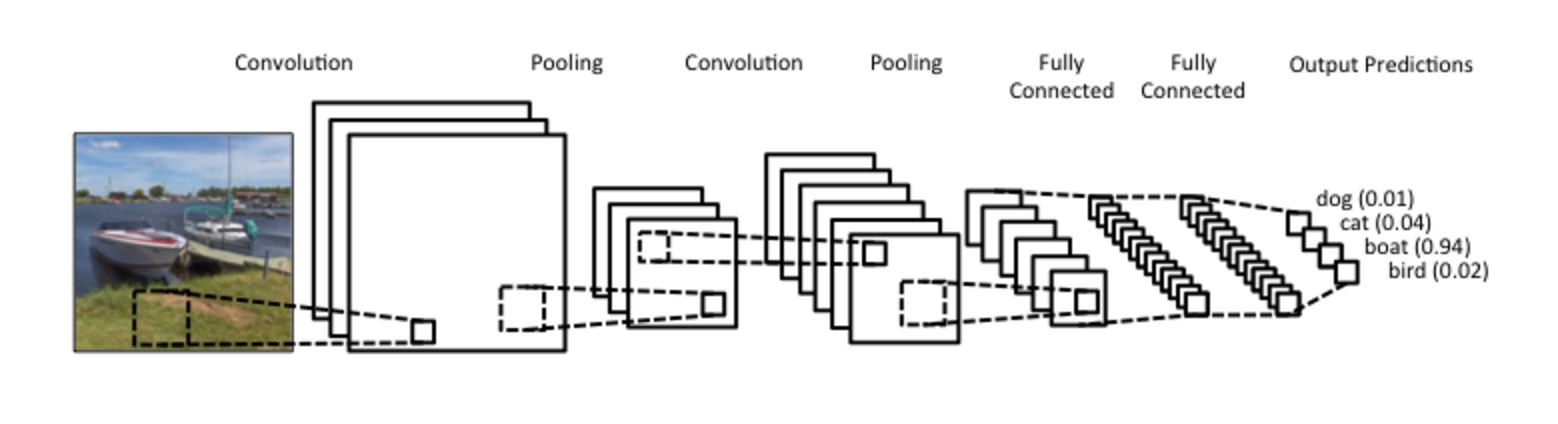
在全連接的多層感知器前

加上卷積層及池化層來抽取特徵

卷積層（Convolution）

把圖片表示為矩陣

-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1

卷積層（Convolution）

選定一個 Kernel

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1

卷積層（Convolution）

從圖片的左上角開始，將 Kernel 疊上去

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1

卷積層（Convolution）

把重疊的項相乘，最後總和

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
(-0.1\times-0.5)+(-0.1\times0)+(0\times0.5)\\ +(-0.25\times-1.0)+(1.0\times0)+(1.0\times1.0)\\ +(-0.5\times-0.5)+(-1.0\times0)+(0.5\times0.5)\\ =1.8

卷積層（Convolution）

把重疊的項相乘，最後總和

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8
(-0.1\times-0.5)+(-0.1\times0)+(0\times0.5)\\ +(-0.25\times-1.0)+(1.0\times0)+(1.0\times1.0)\\ +(-0.5\times-0.5)+(-1.0\times0)+(0.5\times0.5)\\ =1.8

卷積層（Convolution）

平移 Kernel 並重複

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8

卷積層（Convolution）

平移 Kernel 並重複

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8 0.1

卷積層（Convolution）

平移 Kernel 並重複

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8 0.1 -0.575

卷積層（Convolution）

平移 Kernel 並重複

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8 0.1 -0.575
2.25

卷積層（Convolution）

平移 Kernel 並重複

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8 0.1 -0.575
2.25 0

卷積層（Convolution）

平移 Kernel 並重複

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8 0.1 -0.575
2.25 0 -0.75

卷積層（Convolution）

平移 Kernel 並重複

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8 0.1 -0.575
2.25 0 -0.75
1.8

卷積層（Convolution）

平移 Kernel 並重複

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8 0.1 -0.575
2.25 0 -0.75
1.8 0.1

卷積層（Convolution）

平移 Kernel 並重複

-0.5 0 0.5
-1.0 0 1.0
-0.5 0 0.5
-0.1 -0.1 0 0.1 0.25
-0.25 1.0 1.0 1.0 0.3
-0.5 1.0 0.5 1.0 0.5
-0.25 1.0 1.0 1.0 0.2
-0.1 -0.2 0 0 0.1
1.8 0.1 -0.575
2.25 0 -0.75
1.8 0.1 -0.75

卷積層（Convolution）

由卷積的操作可知

卷積運算的結果

與使用的 Kernel 有關

而且有將圖片尺寸略為縮小的副作用

Kernel 不同，抽取出來的特徵也不同

卷積層（Convolution）

CNN 當中的卷積層

每個 Kernel 都會生成一張特徵圖片

所以假設輸入一張 28x28 的圖片

經過有三個 3x3 Kernel 的卷積層後

維度會變成 26x26x3

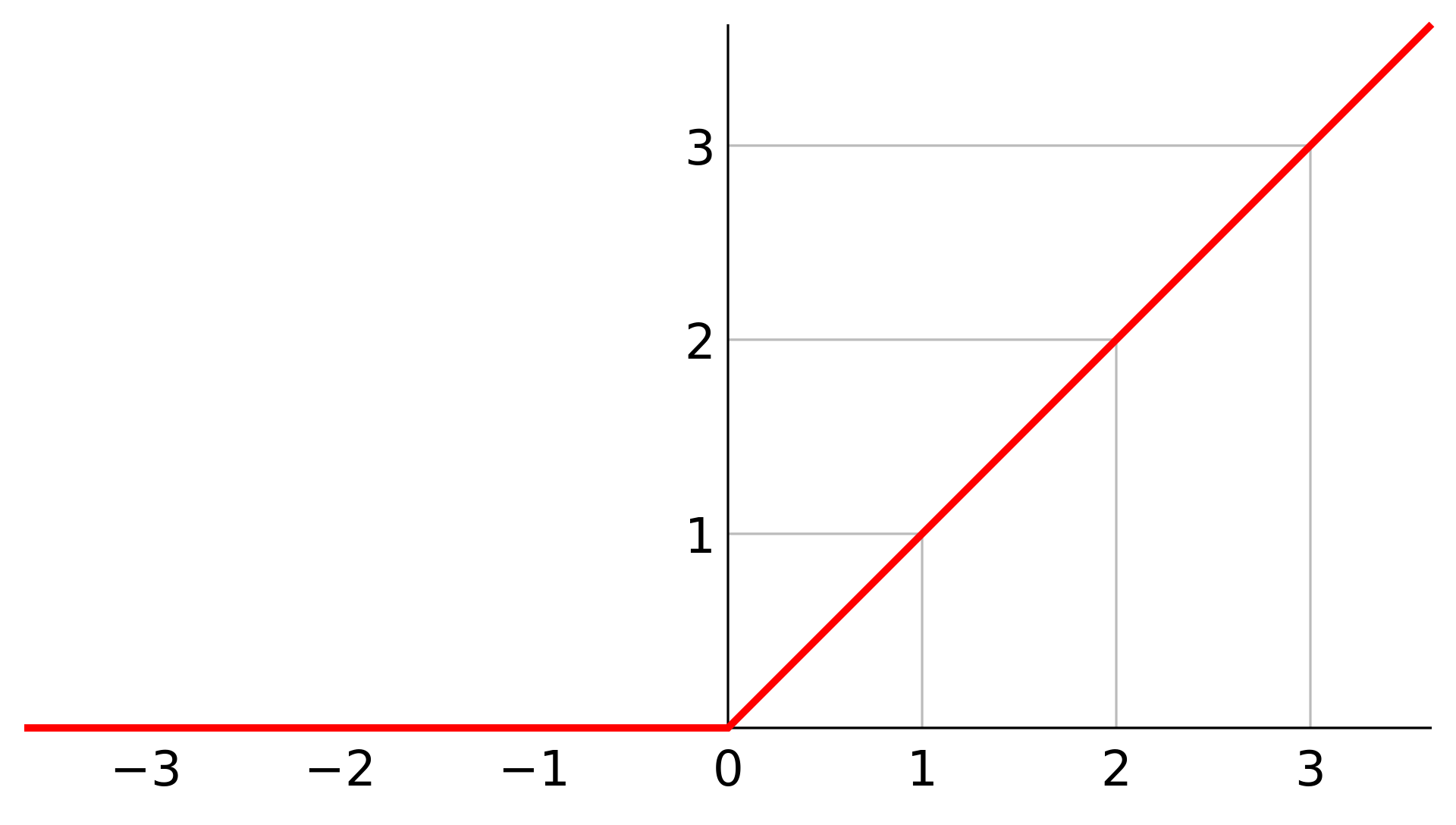
線性整流函式（ReLU）

卷積層的輸出通常會再經過 ReLU 處理

因為它可以去掉負值，進一步簡化

進一步濃縮

當各項特徵透過卷積層抽取出來後

圖片的尺寸跟原本的差不多

這時可以將尺寸縮小

依然可以保留圖片特徵

同時減少了之後所需的運算量

池化層（Pooling）

選一個特定大小的窗口

-0.1 -0.1 0 0.1
-0.25 0.5 0.15 0.2
-0.5 -1.0 0.5 0.3
-0.25 -0.75 0.25 1.0

池化層（Pooling）

疊到圖片上，取窗口內的最大值

-0.1 -0.1 0 0.1
-0.25 0.5 0.15 0.2
-0.5 -1.0 0.5 0.3
-0.25 -0.75 0.25 1.0

池化層（Pooling）

疊到圖片上，取窗口內的最大值

-0.1 -0.1 0 0.1
-0.25 0.5 0.15 0.2
-0.5 -1.0 0.5 0.3
-0.25 -0.75 0.25 1.0
0.5

池化層（Pooling）

平移並重複

-0.1 -0.1 0 0.1
-0.25 0.5 0.15 0.2
-0.5 -1.0 0.5 0.3
-0.25 -0.75 0.25 1.0
0.5 0.2

池化層（Pooling）

平移並重複

-0.1 -0.1 0 0.1
-0.25 0.5 0.15 0.2
-0.5 -1.0 0.5 0.3
-0.25 -0.75 0.25 1.0
0.5 0.2
-0.25

池化層（Pooling）

平移並重複

-0.1 -0.1 0 0.1
-0.25 0.5 0.15 0.2
-0.5 -1.0 0.5 0.3
-0.25 -0.75 0.25 1.0
0.5 0.2
-0.25 1.0

池化層（Pooling）

由此可知，池化層保留特徵

同時減小圖片尺寸

以 2x2 的窗口來說

輸出圖片的長寬將各減少一半

面積則減為四分之一

CNN 結構

這種「抽取特徵」→「縮小尺寸」的過程

會經過多層，直到最後攤平

並送入一般的多層感知器當中

自然語言處理

跟電腦說人話是機器學習的重要目標之一

但是相較於圖片

文字是一種截然不同的資料形式

因為文字是一種「序列式資料」

有順序關係，且輸入的大小不固定

神經網路（NN）

輸入層

隱藏層

輸出層

U
V

神經網路（NN）

U
V
y
h
x

神經網路（NN）

U
V
y
h
x
h=\sigma_h(Ux+b_h)
y=\sigma_y(Vh+b_y)

神經網路（NN）

U
V
y
h
x

循環神經網路（RNN）

U
V
y_t
h_t
x_t
W

循環神經網路（RNN）

U
V
y_t
h_t
x_t
W
U
V
y_{t-1}
h_{t-1}
x_{t-1}
W
\dots
\dots
U
V
y_{t+1}
h_{t+1}
x_{t+1}

循環神經網路（RNN）

U
V
y_t
h_t
x_t
U
V
y_{t-1}
h_{t-1}
x_{t-1}
W
\dots
\dots
h_t=\sigma_h(Ux_t+Wh_{t-1}+b_h)
y_t=\sigma_y(Vh_t+b_y)

循環神經網路（RNN）

U
V
y_t
h_t
x_t
U
V
y_{t-1}
h_{t-1}
x_{t-1}
W
\dots
\dots
h_t=\sigma_h(Ux_t+Wh_{t-1}+b_h)
y_t=\sigma_y(Vh_t+b_y)

先前的資訊

會隨著隱藏層傳播

而有了「記憶」

金魚腦的 RNN

由 RNN 的結構就可以看出

越新的輸入對隱藏狀態的影響越大

先前的資訊則隨時間推移逐漸被遺忘

換言之，簡單 RNN 的記憶力不佳

無法參考太久遠的資訊

長短期記憶（LSTM）

原本的隱藏狀態公式

h_t=\sigma_h(Ux_t+Wh_{t-1}+b_h)

改成

(h_t, c_t)=\mathrm{LSTM}(x_t, h_{t-1}, c_{t-1})

長短期記憶（LSTM）

c_{t-1}
h_{t-1}
x_t
\tanh
\sigma
\sigma
\sigma
\times
\times
+
\tanh
\times
c_t
h_t

隱藏狀態

記憶單元

輸入資料

長短期記憶（LSTM）

圖

例

+
\times

逐項乘法

神經網路（單層）

\tanh

單純的 tanh

（非神經網路）

激勵函數

逐項加法

c_{t-1}
h_{t-1}
x_t
\tanh
\sigma
\sigma
\sigma
\times
\times
+
\tanh
\times
c_t
h_t

隱藏狀態

記憶單元

輸入資料

長短期記憶（LSTM）

c_{t-1}
h_{t-1}
x_t
\tanh
\sigma
\sigma
\sigma
\times
\times
+
\tanh
\times
c_t
h_t

隱藏狀態

記憶單元

輸入資料

長短期記憶（LSTM）

c_{t-1}
h_{t-1}
x_t
\tanh
\sigma
\sigma
\sigma
\times
\times
+
\tanh
\times
c_t
h_t

隱藏狀態

記憶單元

輸入資料

遺忘閘

長短期記憶（LSTM）

c_{t-1}
h_{t-1}
x_t
\tanh
\sigma
\sigma
\sigma
\times
\times
+
\tanh
\times
c_t
h_t

隱藏狀態

記憶單元

輸入資料

輸入閘

長短期記憶（LSTM）

c_{t-1}
h_{t-1}
x_t
\tanh
\sigma
\sigma
\sigma
\times
\times
+
\tanh
\times
c_t
h_t

隱藏狀態

記憶單元

輸入資料

輸出閘

長短期記憶（LSTM）

LSTM 引入記憶單元

c_t

作為神經網路的「長期記憶」

原本的隱藏狀態則成為「短期記憶」

三個閘門也會自己學習何時要拋棄資訊、

從新資訊或短期記憶中儲存資訊、

以及將長期記憶中的資訊「載入」短期記憶中

生成式 AI

對於任務是「無中生有」的 AI

很難用傳統的監督式方法訓練

如（圖片、文字生成）

一個常見的技巧是

讓 AI 生成自己的資料和標籤

生成對抗網路（GAN）

假設要訓練一個可以生成人臉的 AI

可以用兩個神經網路來達成

一個負責生成人臉，為「生成網路」

另一個負責辨識出假人臉，為「判別網路」

以此例子來說，不需要為人臉照片加上標籤

因此為「非監督式學習」

生成對抗網路（GAN）

真實

圖片

生

成

網

路

雜訊

判

別

網

路

真／假

生成對抗網路（GAN）

真實

圖片

生

成

網

路

雜訊

判

別

網

路

真／假

反

向

傳

播

生成對抗網路（GAN）

判別網路要最大化判別圖片真假的準確度

生成網路則要透過生成更像的圖片來最小化它

V(D, G)=\mathbb E_{x\sim p_{\mathrm{data}}(x)}[\log D(x)]+\mathbb E_{z\sim p_z(z)}[\log(1-D(G(z)))]
\displaystyle\min_G\displaystyle\max_D V(D, G)

兩者之間是零和對抗關係

Cross-Entropy

損失函數除了 MSE（均方誤差） 之外

還有一個常用的是 Cross-Entropy

設標籤為 p、輸出為 q

則損失函數為：

\mathcal L=-\displaystyle\sum_ip_i \log q_i

Cross-Entropy

把負號去掉，就變準確度：

在 GAN 裡，輸出只有一個數字

對於真實圖片，D(x) 應接近 1

對於生成的假圖片，D(G(z)) 應接近 0

\displaystyle\sum_ip_i \log q_i

Cross-Entropy

這種情況可以使用 Binary Cross-Entropy

p \log q + (1-p)\log(1-q)

代入 p = 1 的情況（輸入為真實圖片）：

\log q

Cross-Entropy

這種情況可以使用 Binary Cross-Entropy

p \log q + (1-p)\log(1-q)

代入 p = 1 的情況（輸入為真實圖片）：

\log D(x)

Cross-Entropy

這種情況可以使用 Binary Cross-Entropy

p \log q + (1-p)\log(1-q)

代入 p = 0 的情況（輸入為假圖片）：

\log(1-q)

Cross-Entropy

這種情況可以使用 Binary Cross-Entropy

p \log q + (1-p)\log(1-q)

代入 p = 0 的情況（輸入為假圖片）：

\log(1-D(G(z)))

Cross-Entropy

因此可得：

V(D, G)=\mathbb E_{x\sim p_{\mathrm{data}}(x)}[\log D(x)]+\mathbb E_{z\sim p_z(z)}[\log(1-D(G(z)))]

真實圖片的判斷準確度

假圖片的判斷準確度

強化學習（RL）

在強化學習型的任務當中

AI 要操作一個 Agent

這個 Agent 處在一個「環境」當中

Agent 可以根據目前的「狀態」做出「行動」

根據結果，Agent 可以得到對應的「獎勵」

AI 的目標是最大化得到的「獎勵」

馬可夫決策過程

P_a(s, s')=\mathbb P[s_{t+1}=s'|s_t=s,a_t=a]

馬可夫決策過程滿足：

即「轉移到下一個特定狀態的機率

只取決於目前狀態及採取的行動」

且有獎勵

R_a(s, s')

策略與估值

\pi(a|s)=\mathbb P[a_t=a|s_t=s]

策略即為在給定狀態下採取某行動的機率：

對當前狀態的估值會考量未來的潛在報酬：

v_\pi(s)=\mathbb E[\displaystyle\sum_{t=0}^\infin \gamma^{t}r_t|s_0=s]
\pi(s)=a

確定型

隨機型

v_\pi(s)=\displaystyle\sum_{s'}P_{\pi(s)}(s, s')(R_{\pi(s)}(s, s')+\gamma v_\pi(s'))\\

可以將估值函數寫成遞迴式：

策略與估值

此函數給定使用策略，對狀態進行估值

可判斷「狀態的好壞」

策略與估值

Q(s,a)=\displaystyle\sum_{s'}P_a(s, s')(R_a(s, s')+\gamma v_\pi(s'))\\

我們也可以給定狀態

對特定行動估值：

此可判斷「行動的好壞」

Q-Learning

以剛才推導出的 Q 函數為基礎

維護一個 Q 值表

可以輸入狀態與行動，查詢其估值

並透過訓練更新 Q 值表

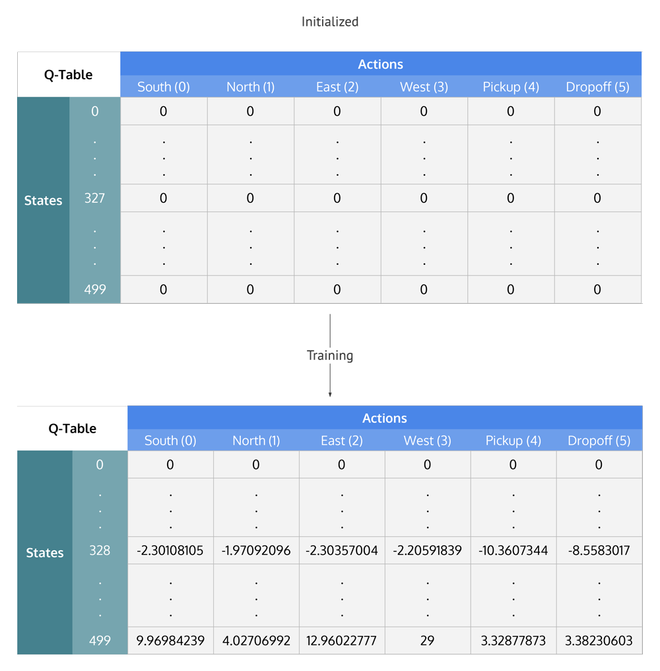
Q_\mathrm{new}(s,a)=(1-\alpha)Q(s,a)+\alpha(r+\gamma\displaystyle\max_{a'}Q(s', a'))

Q-Learning

Deep Q-Learning

在許多情況下（西洋棋、電子遊戲）

可能的狀態根本多到不可能窮舉出來

於是可以把 Q 值表換成神經網路

Q

網

路

s
a_1
a_2
\vdots
a_n
q_1
q_2
q_n

Deep Q-Learning

首先要蒐集樣本

方法是把我們的 Agent 丟到環境裡面

用 Q 網路和 ε-greedy 行動

並記錄狀態、行動、獎勵以及新狀態

註：ε-greedy 指 Agent 有 ε 的機率會隨機行動

否則選擇最好（Q 值最大）的行動

Deep Q-Learning

我們將 Q 網路複製一份

稱為目標網路

Q

網

路

Deep Q-Learning

我們將 Q 網路複製一份

稱為目標網路

Q

網

路

目

標

網

路

Deep Q-Learning

再來從蒐集到的樣本裡選擇一份

Q

網

路

目

標

網

路

(s,a,r,s')

Deep Q-Learning

對 Q 網路輸入 s，得到 a 的 q

Q

網

路

目

標

網

路

(s,a,r,s')
s
q_a

Deep Q-Learning

對目標網路輸入 s'，得到所有 a' 的 q'

Q

網

路

目

標

網

路

(s,a,r,s')
s
q_a
s'
q'_1
q'_2
q'_n
a'_1
a'_2
\vdots
a'_n

Deep Q-Learning

根據 Q 值更新公式，目標 Q 值為：

Q

網

路

目

標

網

路

r+\gamma\displaystyle\max_{a'}q'
s
q_a
s'
q'_1
q'_2
q'_n
a'_1
a'_2
\vdots
a'_n

Deep Q-Learning

此時可定義損失函數：

Q

網

路

目

標

網

路

\mathcal L = (r+\gamma\displaystyle\max_{a'}q'-q_a)^2
s
q_a
s'
q'_1
q'_2
q'_n
a'_1
a'_2
\vdots
a'_n

Deep Q-Learning

用該損失來訓練 Q 網路，目標網路不訓練

Q

網

路

目

標

網

路

\mathcal L = (r+\gamma\displaystyle\max_{a'}q'-q_a)^2
s
q_a
s'
q'_1
q'_2
q'_n
a'_1
a'_2
\vdots
a'_n

訓練

Deep Q-Learning

重複幾次後，再一次複製 Q 網路當目標網路

Q

網

路

\mathcal L = (r+\gamma\displaystyle\max_{a'}q'-q_a)^2
s
q_a

訓練

Deep Q-Learning

重複幾次後，再一次複製 Q 網路當目標網路

Q

網

路

\mathcal L = (r+\gamma\displaystyle\max_{a'}q'-q_a)^2
s
q_a

訓練

目

標

網

路

s'
q'_1
q'_2
q'_n
a'_1
a'_2
\vdots
a'_n

複製

Deep Q-Learning

不斷重複上述過程

Q

網

路

\mathcal L = (r+\gamma\displaystyle\max_{a'}q'-q_a)^2
s
q_a

訓練

目

標

網

路

s'
q'_1
q'_2
q'_n
a'_1
a'_2
\vdots
a'_n

複製

結語

現下許多機器學習演算法都是很新的東西

如生圖的 Diffusion、ChatGPT 的 Transformer 等

希望本課程讓你對於機器學習有大概念的理解

之後也能繼續學習最新的東西

Made with Slides.com