機器學習導論

講師：溫室蔡

機器學習[1]

  • 機器學習的原理
  • 背後的數學概念
  • 手刻人工智慧

我們會教你

  • 使用機器學習框架
  • 怎麼餵 AI 指令
  • AI 相關的哲學問題

我們不會教你

棋類遊戲 圖像生成 自然語言
AlphaGo (2016) DALL-E (2021) GPT-3 (2020)
AlphaGo Zero (2017) MidJourney (2022) LaMDA (2022)
AlphaZero (2018) StableDiffusion (2022) ChatGPT (2022)

機器學習發展趨勢

中文 演算法 人工智慧 機器學習 深度學習
英文 Algorithm Artificial Intelligence
(AI)		 Machine Learning
(ML)		 Deep Learning
(DL)
定義 一套解決問題的流程 表現出智慧的人造機器 透過讓機器自己學習來達成人工智慧 使用神經網路來進行機器學習
範例 廣度優先搜尋 遊戲 NPC 基因演算法 AlphaGo

名詞解釋

三種學習模式

監督式學習

訓練資料集包含

人工貼上的標籤

非監督式學習

資料集不含標籤

只能從資料本身找出模式

強化學習

讓機器根據環境進行決策

再依結果給予獎勵

從一堆已知的資料點

監督式學習－迴歸問題

找出最能正確預測新資料的方程式

線性迴歸（Linear Regression）

(x_i,y_i)
\mathcal{L}(\beta_0, \beta_1)=\displaystyle\sum_{i=0}^{n}(y_i-\hat{y}_i)^2=\displaystyle\sum_{i=0}^{n}(y_i-(\beta_0 +\beta_1 x_i))^2
y=\beta_0+\beta_1 x

微分可以得到函數圖形的「斜率」

重要工具－微分

可以拿來找最大最小值（斜率為 0 處）

y=x^2-3x+2\Rightarrow\dfrac{dy}{dx}=2x-3
2x-3=0\Rightarrow x=\dfrac{3}{2}\text{ has minimum } y

將線性回歸的損失函數

解（簡單）線性迴歸方程式

分別對兩個參數偏微分就可以了

\dfrac{\partial\mathcal{L}}{\partial \beta_0}=0 \Rightarrow \beta_0=\bar{y}-\beta_1\bar{x}
\dfrac{\partial\mathcal{L}}{\partial \beta_1}=0 \Rightarrow \beta_1=\dfrac{\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\displaystyle\sum_{i=1}^{n}(x_i-\bar{x})^2}

將一堆分類好的資料點

監督式學習－分類問題

找出能把它們分割的那條線

支撐向量機（Support Vector Machine）

\vec{w}
\vec{x}_i

支撐向量

\vec{w} \cdot \vec{x} + b=0
\vec{w} \cdot \vec{x} + b=1
\vec{w} \cdot \vec{x} + b=-1

支撐向量機的最小化問題

SVM 要在資料點不落入兩個超平面中間的條件下

使得兩個超平面有最大間隔

兩個超平面的間隔為

\dfrac{2}{||\vec{w}||}

因此目標是「在                                    的條件下，

y_i(\vec{w}\cdot\vec{x}_i+b)\geq1

最小化           。」

||\vec{w}||

其中     為資料點的「顏色」，值為 1 或 -1

y_i

支撐向量機－軟間隔

「硬間隔」SVM 並不好分析，也難以用於真實資料

因此通常使用「軟間隔」，容許部分錯誤分類

此時可定義損失函數：

\mathcal{L}(\vec{w}, b)=\lambda||\vec{w}||^2+\dfrac{1}{n}\displaystyle\sum_{i=1}^{n}\max(0, 1-y_i(\vec{w}\cdot\vec{x}_i+b))

其中    可控制對錯誤分類的容許程度

\lambda

支撐向量機－軟間隔

SVM 的情況不太能像線性回歸那樣一步到位

\dfrac{\partial\mathcal{L}}{\partial \vec{w}}= \begin{cases} 2\lambda\vec{w}-y_ix_i & \text{if $y_i(\vec{w}\cdot\vec{x}_i+b)<1$} \\ 2\lambda\vec{w} & \text{otherwise} \end{cases}

但我們依然可以用偏微分求出梯度來更新參數

\text{For every $i$ : }
\dfrac{\partial\mathcal{L}}{\partial b}= \begin{cases} -y_i & \text{if $y_i(\vec{w}\cdot\vec{x}_i+b)<1$} \\ 0 & \text{otherwise} \end{cases}

支撐向量機－Kernel

對於非線性問題（無法用一條直線分類的問題）

SVM 有時可以透過 Kernel 來解決

平視圖

支撐向量機－Kernel

使用 Kernel：二次方程式

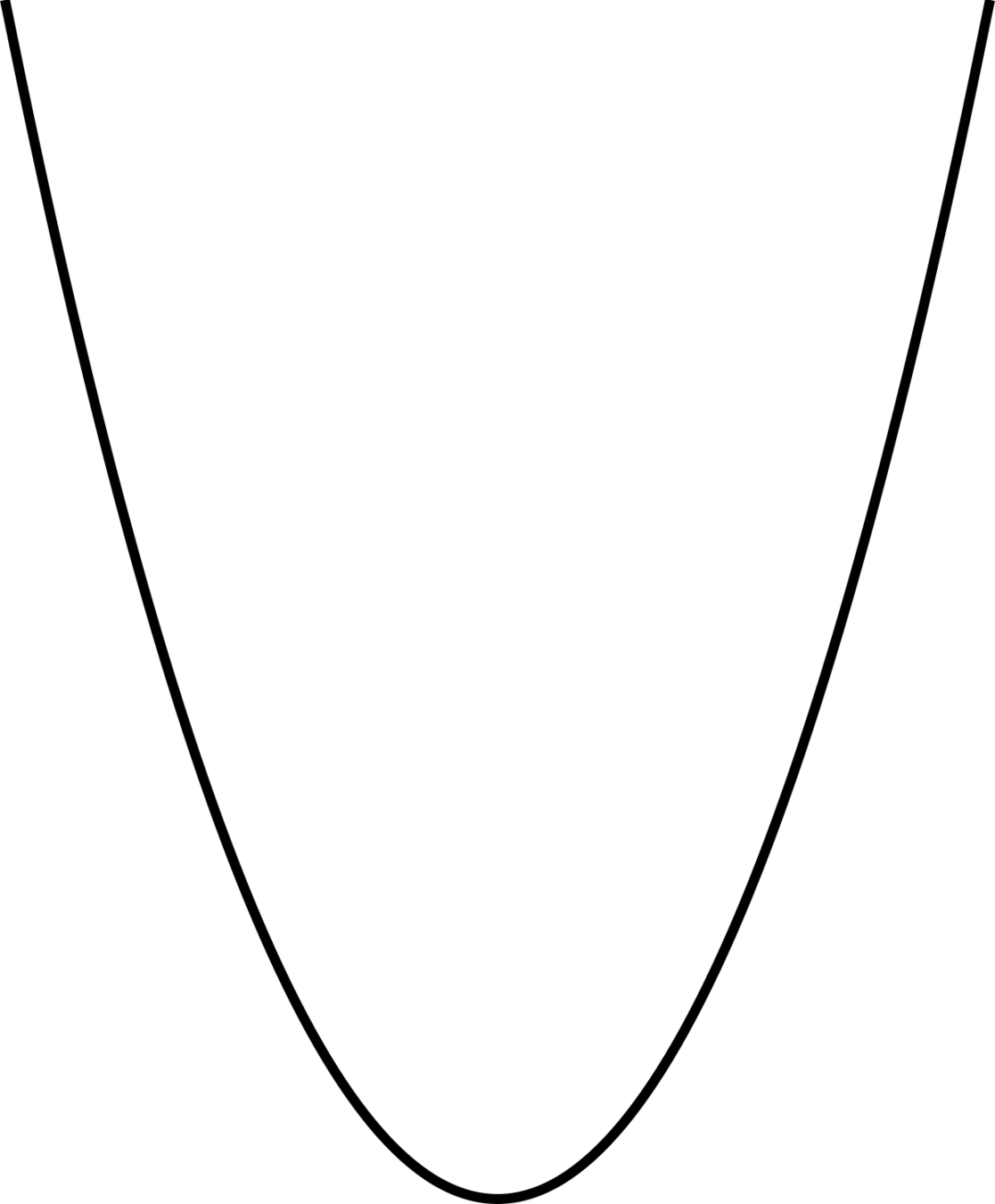
平視圖

一堆沒有標籤的資料點

非監督式學習－聚類問題

要機器自己把相近的分成一類

迭代更新 K 個群心

K-means clustering

以把資料分成 K 類

放置好 K 個群心（註）

K-means 迭代流程

將各個資料點分配到最近的群心

K-means 迭代流程

各群心更新位置到自己群的重心

K-means 迭代流程

重複

K-means 迭代流程

重複

K-means 迭代流程

重複

K-means 迭代流程

重複

K-means 迭代流程

重複

K-means 迭代流程

重複

K-means 迭代流程

重複

K-means 迭代流程

重複

K-means 迭代流程

重複

K-means 迭代流程

完成！

K-means 迭代流程

可以看到 K-means 就跟前面的演算法一樣

K-means 的最小化問題

都有一個要最小化的值

在這裡是「群心與群內各點之距離和」

但它卻不是先以數學分析

而是直接以演算法迭代來達成

群心的初始分布對聚類結果有一定的影響

K-means 群心初始化方法

常用的初始化方式就有三種

  • Forgy：從資料中隨機挑 K 個當初始群心
  • 隨機劃分：把每個資料點隨機分配到 K 個群當中

拿這些群的群心當初始群心

  • K-Means++：一個一個從資料中隨機挑群心

離已經挑過的越遠越容易被挑中

感知器（Perceptron）

x_1
x_2
x_3
\{-1, 1\}
\displaystyle\sum+b
sgn
w_1
w_2
w_3

權重

資料

加總＆加上偏置

激勵函數

輸出

感知器的數學表述

感知器的數學表述與 SVM 極為相似

輸出為

sgn(\vec{w}\cdot\vec{x}+b)

損失函數

\mathcal{L}(\vec{w}, b)=-\dfrac{1}{n}\displaystyle\sum_{i=1}^{n}y_i(\vec{w}\cdot\vec{x}_i+b)
\dfrac{\partial\mathcal{L}}{\partial \vec{w}}=-y_ix_i, \dfrac{\partial\mathcal{L}}{\partial b}=-y_i

感知器的定位

感知器也是一種線性分類器

與 SVM 不同的是，它並不追求最大化邊界

只要找出能分類兩組資料的直線就好

以分類而言其實是比 SVM 差的

那感知器到底有什麼用途呢？

敬請期待

?

Made with Slides.com