FLOw
| Download Speed | Police Chase |
| School Dance | Distinct Routes |
| Parcel Delivery | Task Assignment |
| Distinct Routes II | Distance Queries |
| Grid Puzzle I | Grid Puzzle II |
CSES
LOJ
115、116、117 今天不會講
定義
FLOW?









FLOW?









1
1
1
1
2
2
3
FLOW?

FLOW?
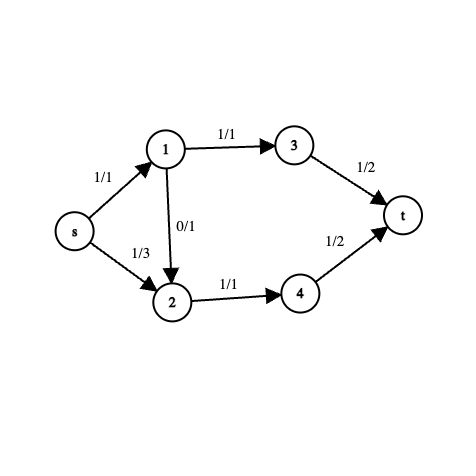
FLOW?

$$|f|=2$$
嚴謹定義
一個流網路(Flow Network)是一張有向圖 \(G=(V,E)\)
- 每條邊有一個非負權重 \(C(u,v)\) 代表邊的流量上限
- 如果 \((u,v) \notin E\),則 \(C(u,v)=0\)
- 有源點 \(s\) (source) 跟匯點 \(t\) (sink)
嚴謹定義
一個流網路上的 s-t 可行流是一個函數 \(f:V \times V \mapsto \mathbb{R} \) 滿足:
- \(f(u,v)\leq c(u,v), \forall (u,v) \in V \times V\) (流量限制)
- \(f(u,v)=-f(v,u), \forall (u,v) \in V \times V\)(流量對稱)
- 對於所有\(v \in V \backslash \{s,t\}\),有\(\sum_{u \in V} f(v,u)=0\)(流量守恆)
嚴謹定義
一個流網路上的 s-t 可行流是一個函數 \(f:V \times V \mapsto \mathbb{R} \) 滿足:
- \(f(u,v)\leq c(u,v), \forall (u,v) \in V \times V\) (流量限制)
- \(f(u,v)=-f(v,u), \forall (u,v) \in V \times V\)(流量對稱)
- 對於所有\(v \in V \backslash \{s,t\}\),有\(\sum\limits_{u \in V} f(v,u)=0\)(流量守恆)
這個 s-t 流的流量為
\(|f|=\sum\limits_{v \in V} f(s,v)=\sum\limits_{u \in t} f(u,t)\)
一個流網路上,\(|f|\)最大的 s-t 流是一個最大流
例子

亂解最大流
無獎徵答

這個網路的最大流是什麼?
無獎徵答

這個網路的最大流是什麼?
\(|f|=4+3+3+1=11\)

亂解最大流
剛剛怎麼找最大流的?
亂解最大流
剛剛怎麼找最大流的?
Greedy 亂做?
每次找一條 s-t 的路流
亂解最大流
剛剛怎麼找最大流的?
Greedy 亂做?
每次找一條 s-t 的路流


亂解最大流
剛剛怎麼找最大流的?
Greedy 亂做?
每次找一條 s-t 的路流


\(|f|=1\)
Greedy vs. 最大流


Greedy
最大流
差了什麼?
Greedy vs. 最大流


Greedy
最大流
差了什麼?
流回去
流回去
可以:
- 從1號點流2流量給2號點
- 從2號點倒流3流量給1號點

流回去
可以:
- 從1號點流2流量給2號點
- 從2號點倒流3流量給1號點
Recall: \(f(2,1)=-f(1,2)=-3\)、\(c(2,1)=0\)

剩餘網路
定義:兩點間的剩餘流量 (residual capacity) 為:
\(r(u,v)=c(u,v)-f(u,v)\)
也就是這條邊還可以再(倒)流的量
剩餘網路
定義:兩點間的剩餘流量 (residual capacity) 為:
\(r(u,v)=c(u,v)-f(u,v)\)
也就是這條邊還可以再(倒)流的量
所有 \(r(u,v)>0\) 的邊構成的圖稱為剩餘網路 (residual network)
圖 \(G\) 上的一組流 \(f\) 的剩餘網路記作 \(G_f\)
剩餘網路
定義:兩點間的剩餘流量 (residual capacity) 為:
\(r(u,v)=c(u,v)-f(u,v)\)
也就是這條邊還可以再(倒)流的量
所有 \(r(u,v)>0\) 的邊構成的圖稱為剩餘網路 (residual network)
圖 \(G\) 上的一組流 \(f\) 的剩餘網路記作 \(G_f\)
剩餘網路上一組 s-t 路徑稱為擴充路徑(Augmenting Path)
修好的greedy
- 在剩餘網路找一條擴充路徑
- 往他塞滿流
- 找不到擴充路徑的話就是最大流了
修好的greedy
- 在剩餘網路找一條擴充路徑
- 往他塞滿流
- 找不到擴充路徑的話就是最大流了
屁啦
證明呢
最大流最小割定理 (MFMC)
割?
圖的「割」:把圖分成兩群
中間的邊把他🈹掉
割?
圖的「割」:把圖分成兩群
中間的邊把他🈹掉
定義:一個 s-t 割 (cut) \(C\) 是一個滿足 \(s \in S, t \in T\) 的割
- \(S+T=V\)、\(S\cap T = \{\} \)
- 在流網路中,一個 s-t 割的大小為 \(|C|=\sum\limits_{u \in S} \sum\limits_{v \in T} c(u,v)\)
- 也就是所有從 \(S\) 到 \(T\) 的邊的流量上限和
- \(T\) 到 \(S\) 的不算!
- 最小割是大小最小的 s-t 割
一些lemma
- \(f(S,T)=\sum\limits_{u \in S} \sum\limits_{v \in T} f(u,v)\)
- 則\(|f|=f(S,T)\leq c(S,T)\)
一些lemma
- \(f(S,T)=\sum\limits_{u \in S} \sum\limits_{v \in T} c(u,v)\)
- 則\(|f|=f(S,T)\leq c(S,T)\)
任意一組 s-t 流 \(\leq\) 任意一組 s-t 割
一些lemma
- \(f(S,T)=\sum\limits_{u \in S} \sum\limits_{v \in T} c(u,v)\)
- 則\(|f|=f(S,T)\leq c(S,T)\)
任意一組 s-t 流 \(\leq\) 任意一組 s-t 割
最大流 \(\leq\) 最小割!
到底找不找得到呢?
一些lemma
- \(f(S,T)=\sum\limits_{u \in S} \sum\limits_{v \in T} c(u,v)\)
- 則\(|f|=f(S,T)\leq c(S,T)\)
任意一組 s-t 流 \(\leq\) 任意一組 s-t 割
最大流 \(\leq\) 最小割!
到底找不找得到呢?可以!
最大流最小割定理
(Max Flow Min Cut Theorem)
對一個流量網路 \(G\) ,以下三者等價:
- \(f\) 是一個 s-t 最大流
- \(G_f\) 沒有從 \(s\) 到 \(t\) 的擴充路徑
- \(|f| = |C|\),其中 \(C\) 是 s-t 最小割
最大流最小割定理
(Max Flow Min Cut Theorem)
對一個流量網路 \(G\) ,以下三者等價:
- \(f\) 是一個 s-t 最大流
- \(G_f\) 沒有從 \(s\) 到 \(t\) 的擴充路徑
- \(|f| = |C|\),其中 \(C\) 是 s-t 最小割
也就是 最大流 = 最小割,而且greedy亂做是對的
最大流最小割定理
(Max Flow Min Cut Theorem)
證明:(1) -> (2)
假設 \(G_f\) 有擴充路徑,那走完這條之後 \(|f|\) 會更大,矛盾
最大流最小割定理
(Max Flow Min Cut Theorem)
證明:(2) -> (3)
令 \(S\) 為 \(s\) 在 \(G_f\) 上所有能走到的點,\(T=V \backslash S\)

最大流最小割定理
(Max Flow Min Cut Theorem)
證明:(2) -> (3)
令 \(S\) 為 \(s\) 在 \(G_f\) 上所有能走到的點,\(T=V \backslash S\)
- \(S,T\) 是一個🈹
- \(|f|=|f(S,T)|\) (Lemma)
- \(S\) 到 \(T\) 的邊都流滿(不然會在 \(G_f\) 上)
- \(T\) 到 \(S\) 的邊都沒流(不然會在 \(G_f\) 上)
- \(|f|=|f(S,T)|=|C|\)
最大流最小割定理
(Max Flow Min Cut Theorem)
證明:(3) -> (1)
- \(|f| \leq |C|\)
- 剛剛構造了一個 \((S,T)\) 使 \(|C|=|f|\)
最大流最小割定理
(Max Flow Min Cut Theorem)
證明:(3) -> (1)
- \(|f| \leq |C|\)
- 剛剛構造了一個 \((S,T)\) 使 \(|C|=|f|\)
構解:\(S\) 為 \(s\) 在 \(G_f\) 上所有能走到的點,\(T=V \backslash S\)
最大流演算法
Ford-Fulkerson & Capacity Scaling
Ford-fulkerson
MFMC 說 greedy 是對的
Ford-fulkerson
MFMC 說 greedy 是對的
演算法:
- while \(G_f\) 上有擴充路徑
- 找一條擴充
好簡單
Ford-fulkerson
MFMC 說 greedy 是對的
演算法:
- while \(G_f\) 上有擴充路徑
- 找一條擴充
好簡單
找路徑?DFS
流多少?擴充路徑上剩餘流量的最小值
Code
#include<iostream>
#include<vector>
#include<algorithm>
#include<utility>
using namespace std;
typedef long long ll;
const ll inf = INT32_MAX;
struct edge{
int v, c, r, rid;
edge(int _v, int _c, int _r, int _rid){
v = _v, c = _c, r = _r, rid = _rid;
}
// rid: 存反向邊編號
};
struct ff{
vector<vector<edge>> graph;
vector<bool> vis;
ff(int n){
graph.resize(n + 1);
vis.resize(n + 1);
}
void add(int a, int b, int c, int rc = 0){
// rc: 無向圖時用
graph[a].emplace_back(b, c, c, (int)graph[b].size());
graph[b].emplace_back(a, rc, rc, (int)graph[a].size() - 1);
}
int dfs(int u, int t, int cap){
// cap: 瓶頸大小
if(cap == 0) return 0; // 涼了
if(u == t) return cap; // 到t了
vis[u] = 1;
for(auto &[v, c, r, rid]: graph[u]){
if(!vis[v]){
int flow_val = dfs(v, t, min(cap, r));
if(flow_val != 0){
r -= flow_val;
graph[v][rid].r += flow_val;
return flow_val;
}
}
}
return 0;
}
ll flow(int s, int t){
// 記得開long long
ll ans = 0, flow_val;
while((flow_val = dfs(s, t, inf)) > 0){
ans += flow_val;
fill(vis.begin(), vis.end(), 0);
}
return ans;
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n, m, s, t;
cin >> n >> m >> s >> t;
ff flow(n);
int a, b, c;
for(int i = 0; i < m; i++){
cin >> a >> b >> c;
flow.add(a, b, c);
}
cout << flow.flow(s, t) << "\n";
}複雜度分析

複雜度分析

誰在搞事

誰在搞事

唬爛2:
假設最大邊權為 \(U\)
先只看 \(G_f\) 中剩餘流量 \(\geq\) \(U\) 的邊
再看 \(\geq \frac{U}{2}\) 的邊
再看 \(\geq \frac{U}{4}\) 的邊
...
CODE
#include<iostream>
#include<vector>
#include<algorithm>
#include<utility>
using namespace std;
typedef long long ll;
const ll inf = INT32_MAX;
struct edge{
int v, c, r, rid;
edge(int _v, int _c, int _r, int _rid){
v = _v, c = _c, r = _r, rid = _rid;
}
// rid: 存反向邊編號
};
struct ff{
vector<vector<edge>> graph;
vector<bool> vis;
int maxi = 0;
ff(int n){
graph.resize(n + 1);
vis.resize(n + 1);
}
void add(int a, int b, int c, int rc = 0){
// rc: 無向圖時用
graph[a].emplace_back(b, c, c, (int)graph[b].size());
graph[b].emplace_back(a, rc, rc, (int)graph[a].size() - 1);
maxi = max(maxi, c);
maxi = max(maxi, rc);
}
int dfs(int u, int t, int cap, int delta){
// cap: 瓶頸大小
if(cap < delta) return 0; // 涼了
if(u == t) return cap; // 到t了
vis[u] = 1;
for(auto &[v, c, r, rid]: graph[u]){
if(!vis[v]){
int flow_val = dfs(v, t, min(cap, r), delta);
if(flow_val != 0){
r -= flow_val;
graph[v][rid].r += flow_val;
return flow_val;
}
}
}
return 0;
}
ll flow(int s, int t, int delta){
// 記得開long long
ll ans = 0, flow_val;
while((flow_val = dfs(s, t, inf, delta)) > 0){
ans += flow_val;
fill(vis.begin(), vis.end(), 0);
}
return ans;
}
ll scale(int s, int t){
ll ans = 0;
while(maxi > 0){
fill(vis.begin(), vis.end(), 0);
ans += flow(s, t, maxi);
maxi /= 2;
}
return ans;
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n, m, s, t;
cin >> n >> m >> s >> t;
ff flow(n);
int a, b, c;
for(int i = 0; i < m; i++){
cin >> a >> b >> c;
flow.add(a, b, c);
}
cout << flow.scale(s, t) << "\n";
}正確性證明
- 假設現在只看剩餘流量 \(\geq D\) 的邊
- \(G_f(D)\) 為這樣子的剩餘網路
- \(D=1\)時,\(G_f(D)=G_f\)
- 所以是對的,只是前面多跑了幾次 FF 而已
複雜度分析
複雜度突然變 \(|E|^2 logU\) 了!
複雜度分析
複雜度突然變 \(|E|^2 logU\) 了!
證明:
- 假設現在只看 \(\geq D\) 的邊,叫做一個 D-scaling phase
- \(D\) 每次被砍半,所以只會有 \(O(log(U))\) 次 phases
複雜度分析
複雜度突然變 \(|E|^2 logU\) 了!
證明:
- 假設現在只看 \(\geq D\) 的邊,叫做一個 D-scaling phase
- \(D\) 每次被砍半,所以只會有 \(O(log(U))\) 次 phases
- Lemma 1:在 D-scaling phase 結束後,目前找到的 \(|f|\) 最多只比最大流大小 \(|f_{max}|\) 小 \(D\cdot |E|\)
- 證明:設 \(S\) 是 \(G_f(U)\) 中從 \(s\) 走得到的點,其他為 \(T\)
- 跟證 MFMC 一模一樣
- S-T 割中的邊每條剩餘流量都小於 \(D\)
- \(|f|+D\cdot |E| \geq |C(S,T)| \geq |f_{max}|\)
- 證明:設 \(S\) 是 \(G_f(U)\) 中從 \(s\) 走得到的點,其他為 \(T\)
複雜度分析
複雜度突然變 \(|E|^2 logU\) 了!
證明:
- 假設現在只看 \(\geq D\) 的邊,叫做一個 D-scaling phase
- \(D\) 每次被砍半,所以只會有 \(O(log(U))\) 次 phases
- Lemma 2:一個 D-scaling phase 最多擴充 \(2 \cdot |E|\) 次
- 2D-scaling phase 結束後,\(|f|+2D\cdot |E| \geq |f_{max}|\)
- 一次擴充最少擴充 \(D\)
- 最多擴充 \(2|E|\) 次就滿了
複雜度分析
複雜度突然變 \(|E|^2 logU\) 了!
證明:
- 假設現在只看 \(\geq D\) 的邊,叫做一個 D-scaling phase
- \(D\) 每次被砍半,所以只會有 \(O(log(U))\) 次 phases
- \(O(log(U))\) 次 phase
- 一次 phase 擴充 \(O(|E|)\)次
- 一次擴充花 \(O(|E|)\)
- 總複雜度 \(O(|E|^2logU)\)
複雜度分析
複雜度突然變 \(|E|^2 logU\) 了!
其實這樣已經可以過所有CSES題了 (flow很難跑到 worst-case)
更快的Flow
Edmonds-Karp, Dinic (Dinitz)
Ford-fulkerson
演算法:
- while \(G_f\) 上有擴充路徑
- 找一條擴充
EDmonds-karp
演算法:
- while \(G_f\) 上有擴充路徑
- 找一條 \(G_f\)上的最短路 擴充
EDmonds-karp
演算法:
- while \(G_f\) 上有擴充路徑
- 找一條 \(G_f\)上的最短路 擴充
\(O(|E|\cdot |f|)\) -> \(O(|V|\cdot|E|^2)\)!
證明
兩個 lemma:
- 令 \(d_f(u)\) 為 \(G_f\) 上 \(s\) 到 \(u\) 的最短路長
- Lemma 1:在 Edmonds-Karp 中,\(d_f(u)\) 不會減少
- 令一條邊 \((u,v)\) 為緊邊代表它是目前擴充路徑上剩餘流量最小的一條邊
- Lemma 2:每條邊最多成為 \(O(V)\) 次緊邊
證明
兩個 lemma:
- 令 \(d_f(u)\) 為 \(G_f\) 上 \(s\) 到 \(u\) 的最短路長
- Lemma 1:在 Edmonds-Karp 中,\(d_f(u)\) 不會減少
- 令一條邊 \((u,v)\) 為緊邊代表它是目前擴充路徑上剩餘流量最小的一條邊
- Lemma 2:每條邊最多成為 \(O(V)\) 次緊邊
一次擴充一條緊邊 -> 最多擴充 \(O(VE)\) 次 -> 總複雜度 \(O(VE^2)\)
證明
Lemma 1 證明:
- 假設一次擴充完,流從 \(f\) 變成 \(f'\)
- 某個點 \(u\) 的距離從 \(d_f(u)\) 變成 \(d_{f'}(u)\)
- 假設這個 \(u\) 是所有距離減少的點中 \(d_{f'}(u)\) 最小的
- 令 \(G_{f'}\) 中最短路為 s -> v -> u
- \(d_{f'}(v)\) 沒減少
- 令 \(G_{f'}\) 中最短路為 s -> v -> u
- \((v,u) \notin E(G_f)\)
- 不然 \(d_f(u) \leq d_f(v)+1 \leq d_{f'}(v)+1=d_{f'}(u)<d_f(u)\)
- \((v,u) \in E(G_{f'})\),所以 \(f\) 到 \(f'\) 有走過 \((u,v)\)
- 但 \(d_f(u)=d_f(v)-1\leq d_{f'}(v)-1=d_{f'}(u)-2<d_f(u)-2\)
- 所以 \(d_f(u)\) 永遠不會減少
證明
Lemma 2 證明:
- 假設一次擴充完,\(u,v\) 是緊邊
- 擴充前 \(d_f(v)=d_f(u)+1\)
- 擴充完 \((u,v) \notin E(G_{f'})\)
- \((u,v)\) 要變成緊邊一定要從 \((v,u)\) 擴充過
- \((v,u)\) 擴充完,\(d_{f'}(u)=d_{f'}(v)+1\geq d_f(v)+1=d_f(u)+2\)
- \(d(u)\) 至少增加 2
- 最多增加 \(|V|\),所以最多成為緊邊 \(O(|V|)\) 次
CODE
#include<iostream>
#include<vector>
#include<algorithm>
#include<utility>
#include<queue>
using namespace std;
typedef long long ll;
const ll inf = INT32_MAX;
struct edge{
int v, c, r, rid;
edge(int _v, int _c, int _r, int _rid){
v = _v, c = _c, r = _r, rid = _rid;
}
// rid: 存反向邊編號
};
struct ek{
vector<vector<edge>> graph;
vector<bool> vis;
vector<int> dist;
ek(int n){
graph.resize(n + 1);
vis.resize(n + 1);
dist.resize(n + 1);
}
void add(int a, int b, int c, int rc = 0){
// rc: 無向圖時用
graph[a].emplace_back(b, c, c, (int)graph[b].size());
graph[b].emplace_back(a, rc, rc, (int)graph[a].size() - 1);
}
bool bfs(int s, int t){
fill(dist.begin(), dist.end(), inf);
queue<int> q;
q.push(s);
dist[s] = 0;
while(!q.empty()){
auto node = q.front();
q.pop();
for(auto &[v, c, r, rid]: graph[node]){
if(r > 0 && dist[v] == inf){
dist[v] = dist[node] + 1;
q.push(v);
}
}
}
return dist[t] < inf;
}
int dfs(int u, int t, int cap){
// cap: 瓶頸大小
if(cap == 0) return 0; // 涼了
if(u == t) return cap; // 到t了
vis[u] = 1;
for(auto &[v, c, r, rid]: graph[u]){
if(!vis[v] && dist[v] == dist[u] + 1){
int flow_val = dfs(v, t, min(cap, r));
if(flow_val != 0){
r -= flow_val;
graph[v][rid].r += flow_val;
return flow_val;
}
}
}
return 0;
}
ll flow(int s, int t){
// 記得開long long
ll ans = 0, flow_val;
while(bfs(s, t)){
fill(vis.begin(), vis.end(), 0);
while((flow_val = dfs(s, t, inf)) > 0){
ans += flow_val;
fill(vis.begin(), vis.end(), 0);
}
}
return ans;
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n, m, s, t;
cin >> n >> m >> s >> t;
ek flow(n);
int a, b, c;
for(int i = 0; i < m; i++){
cin >> a >> b >> c;
flow.add(a, b, c);
}
cout << flow.flow(s, t) << "\n";
}CODE
#include<iostream>
#include<vector>
#include<algorithm>
#include<utility>
#include<queue>
using namespace std;
typedef long long ll;
const ll inf = INT32_MAX;
struct edge{
int v, c, r, rid;
edge(int _v, int _c, int _r, int _rid){
v = _v, c = _c, r = _r, rid = _rid;
}
// rid: 存反向邊編號
};
struct ek{
vector<vector<edge>> graph;
vector<bool> vis;
vector<int> dist;
int maxi = 0;
ek(int n){
graph.resize(n + 1);
vis.resize(n + 1);
dist.resize(n + 1);
}
void add(int a, int b, int c, int rc = 0){
// rc: 無向圖時用
graph[a].emplace_back(b, c, c, (int)graph[b].size());
graph[b].emplace_back(a, rc, rc, (int)graph[a].size() - 1);
maxi = max(maxi, c);
maxi = max(maxi, rc);
}
bool bfs(int s, int t, int delta){
fill(dist.begin(), dist.end(), inf);
queue<int> q;
q.push(s);
dist[s] = 0;
while(!q.empty()){
auto node = q.front();
q.pop();
for(auto &[v, c, r, rid]: graph[node]){
if(r >= delta && dist[v] == inf){
dist[v] = dist[node] + 1;
q.push(v);
}
}
}
return dist[t] < inf;
}
int dfs(int u, int t, int cap, int delta){
// cap: 瓶頸大小
if(cap < delta) return 0; // 涼了
if(u == t) return cap; // 到t了
vis[u] = 1;
for(auto &[v, c, r, rid]: graph[u]){
if(!vis[v] && dist[v] == dist[u] + 1){
int flow_val = dfs(v, t, min(cap, r), delta);
if(flow_val != 0){
r -= flow_val;
graph[v][rid].r += flow_val;
return flow_val;
}
}
}
return 0;
}
ll flow(int s, int t, int delta){
// 記得開long long
ll ans = 0, flow_val;
while(bfs(s, t, delta)){
fill(vis.begin(), vis.end(), 0);
while((flow_val = dfs(s, t, inf, delta)) > 0){
ans += flow_val;
fill(vis.begin(), vis.end(), 0);
}
}
return ans;
}
ll scale(int s, int t){
ll ans = 0;
while(maxi > 0){
fill(vis.begin(), vis.end(), 0);
ans += flow(s, t, maxi);
maxi /= 2;
}
return ans;
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n, m, s, t;
cin >> n >> m >> s >> t;
ek flow(n);
int a, b, c;
for(int i = 0; i < m; i++){
cin >> a >> b >> c;
flow.add(a, b, c);
}
cout << flow.scale(s, t) << "\n";
}當然也可以 scaling
還要更快
Edmonds-Karp 浪費時間在哪?
每次最短路都要重跑一次
還要更快
Edmonds-Karp 浪費時間在哪?
每次最短路都要重跑一次
先把最短路 DAG 找出來

還要更快
假設現在有條邊沒有用了..

還要更快
假設現在有條邊沒有用了..
下次直接從下一條邊開始找擴充路徑!

還要更快
假設現在有條邊沒有用了..
下次直接從下一條邊開始找擴充路徑!
對於每個點 \(u\) ,紀錄這個點目前跑到的邊 \(it(u)\)
下次直接從 \(it(u)\) 開始跑

還要更快

CODE
#include<iostream>
#include<vector>
#include<algorithm>
#include<utility>
#include<queue>
using namespace std;
typedef long long ll;
const ll inf = INT32_MAX;
struct edge{
int v, c, r, rid;
edge(int _v, int _c, int _r, int _rid){
v = _v, c = _c, r = _r, rid = _rid;
}
// rid: 存反向邊編號
};
struct dinic{
vector<vector<edge>> graph;
vector<bool> vis;
vector<int> dist, it;
dinic(int n){
graph.resize(n + 1);
vis.resize(n + 1);
dist.resize(n + 1);
it.resize(n + 1);
}
void add(int a, int b, int c, int rc = 0){
// rc: 無向圖時用
graph[a].emplace_back(b, c, c, (int)graph[b].size());
graph[b].emplace_back(a, rc, rc, (int)graph[a].size() - 1);
}
bool bfs(int s, int t){
fill(dist.begin(), dist.end(), inf);
queue<int> q;
q.push(s);
dist[s] = 0;
while(!q.empty()){
auto node = q.front();
q.pop();
for(auto &[v, c, r, rid]: graph[node]){
if(r > 0 && dist[v] == inf){
dist[v] = dist[node] + 1;
q.push(v);
}
}
}
return dist[t] < inf;
}
int dfs(int u, int t, int cap){
// cap: 瓶頸大小
if(cap == 0) return 0; // 涼了
if(u == t) return cap; // 到t了
vis[u] = 1;
for(int &i = it[u]; i < (int)graph[u].size(); i++){
auto &[v, c, r, rid] = graph[u][i];
if(!vis[v] && dist[v] == dist[u] + 1){
int flow_val = dfs(v, t, min(cap, r));
if(flow_val != 0){
r -= flow_val;
graph[v][rid].r += flow_val;
return flow_val;
}
}
}
return 0;
}
ll flow(int s, int t){
// 記得開long long
ll ans = 0, flow_val;
while(bfs(s, t)){
fill(vis.begin(), vis.end(), 0);
fill(it.begin(), it.end(), 0);
while((flow_val = dfs(s, t, inf)) > 0){
ans += flow_val;
fill(vis.begin(), vis.end(), 0);
}
}
return ans;
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n, m, s, t;
cin >> n >> m >> s >> t;
dinic flow(n);
int a, b, c;
for(int i = 0; i < m; i++){
cin >> a >> b >> c;
flow.add(a, b, c);
}
cout << flow.flow(s, t) << "\n";
}CODE
#include<iostream>
#include<vector>
#include<algorithm>
#include<utility>
#include<queue>
using namespace std;
typedef long long ll;
const ll inf = INT32_MAX;
struct edge{
int v, c, r, rid;
edge(int _v, int _c, int _r, int _rid){
v = _v, c = _c, r = _r, rid = _rid;
}
// rid: 存反向邊編號
};
struct dinic{
vector<vector<edge>> graph;
vector<bool> vis;
vector<int> dist, it;
int maxi = 0;
dinic(int n){
graph.resize(n + 1);
vis.resize(n + 1);
dist.resize(n + 1);
it.resize(n + 1);
}
void add(int a, int b, int c, int rc = 0){
// rc: 無向圖時用
graph[a].emplace_back(b, c, c, (int)graph[b].size());
graph[b].emplace_back(a, rc, rc, (int)graph[a].size() - 1);
maxi = max(maxi, c);
maxi = max(maxi, rc);
}
bool bfs(int s, int t, int delta){
fill(dist.begin(), dist.end(), inf);
queue<int> q;
q.push(s);
dist[s] = 0;
while(!q.empty()){
auto node = q.front();
q.pop();
for(auto &[v, c, r, rid]: graph[node]){
if(r > 0 && dist[v] == inf && r >= delta){
dist[v] = dist[node] + 1;
q.push(v);
}
}
}
return dist[t] < inf;
}
int dfs(int u, int t, int cap, int delta){
// cap: 瓶頸大小
if(cap < delta) return 0; // 涼了
if(u == t) return cap; // 到t了
vis[u] = 1;
for(int &i = it[u]; i < (int)graph[u].size(); i++){
auto &[v, c, r, rid] = graph[u][i];
if(!vis[v] && dist[v] == dist[u] + 1){
int flow_val = dfs(v, t, min(cap, r), delta);
if(flow_val != 0){
r -= flow_val;
graph[v][rid].r += flow_val;
return flow_val;
}
}
}
return 0;
}
ll flow(int s, int t, int delta){
// 記得開long long
ll ans = 0, flow_val;
while(bfs(s, t, delta)){
fill(vis.begin(), vis.end(), 0);
fill(it.begin(), it.end(), 0);
while((flow_val = dfs(s, t, inf, delta)) > 0){
ans += flow_val;
fill(vis.begin(), vis.end(), 0);
}
}
return ans;
}
ll scale(int s, int t){
ll ans = 0;
while(maxi > 0){
ans += flow(s, t, maxi);
maxi /= 2;
}
return ans;
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n, m, s, t;
cin >> n >> m >> s >> t;
dinic flow(n);
int a, b, c;
for(int i = 0; i < m; i++){
cin >> a >> b >> c;
flow.add(a, b, c);
}
cout << flow.scale(s, t) << "\n";
}又可以 scaling 了
複雜度分析
\(O(V^2E)\)
可以想像成把Edmonds-Karp的一個 \(E\) 壓成 \(V\)
證明:
- 每個點要試的點數不超過 \(deg(u)\)
- 全部人要試的點數不超過 \(O(|E|)\)
- 每次擴充會有一條邊變緊邊
- 有人的 \(it(u)\) 會增加
- 最多擴充 \(O(|E|)\) 次
- 每次擴充路徑長為 \(O(k)\)
- 擴充所有同樣長度的路徑要 \(O(k|E|)\)
- 總複雜度 \(\sum\limits_{k=1}^{|V|-1} O(k|E|)=O(|V|^2|E|)\)
複雜度分析
更爽的特例:
- 單位流網路中是 \(O(min(V^{2/3},E^{1/2}))\)
- 二分圖匹配網路中是 \(O(\sqrt{V} E)\)
二分圖匹配是 \(O(\sqrt{V} E)\) 的證明:
-
擴充完 \(1\) ~ \(\sqrt{|V|}\) 的路徑後,剩下的每條擴充路徑長度都 \(\geq \sqrt{|V|}\)
- 這部分是 \(O(\sqrt{V} E)\)
- 每個點都只會有最多一條擴充路徑經過他
- 所以剩下的擴充路徑數 \(\leq \sqrt {|V|}\)
- 擴充一條路徑花 \(O(|E|)\) 的時間,所以這部分也是 \(O(\sqrt{V} E)\)
- 所以加起來就是 \(O(\sqrt{V} E)\)
例題
小聲明
講師不會備課所以聽不懂很正常
可以先把 Dinic 想像成一個會輸出最大流的黑盒子
有 \(n\) 台機器跟 \(m\) 條電纜,每條電纜連接 \(u,v)\),有一個頻寬上限 \(c\)
請問從機器 1 傳訊到機器 \(n\) 的最大頻寬為多少?
- \(n \leq 500\)
- \(m \leq 1000\)
- \(c \leq 10^9\)
最小割裸題
還記得怎麼構解嗎?
有 \(n\) 個男生跟 \(m\) 個女生,有 \(k\) 對男生跟女生想一起跳舞
一個人只能跟另一個人跳舞,請問最多可以湊成幾對舞伴?
P. S. Happy Pride Month
- \(1 \leq n,m \leq 500\)
- \(1 \leq k \leq 1000\)
二分圖匹配
\(s\) 跟 \(t\) 怎麼辦?
二分圖匹配
\(s\) 跟 \(t\) 怎麼辦?
把所有源點連到超源點、所有匯點連到超匯點

我真的沒時間了燒雞
這些是上課可能會講得例題
最小費用(最大)流
Min Cost Max Flow
定義
一個費用流網路(Flow Network)是一張有向圖 \(G=(V,E)\)
- 每條邊有一個非負權重 \(C(u,v)\) 代表邊的流量上限
- 和一個實數權重 \(W(u,v)\) 代表邊的費用
- 如果 \((u,v) \notin E\),則 \(C(u,v)=0\)
- 有源點 \(s\) (source) 跟匯點 \(t\) (sink)
定義
一個費用流網路上的 s-t 可行流是一個函數 \(f:V \times V \mapsto \mathbb{R} \) 滿足:
- \(f(u,v)\leq c(u,v), \forall (u,v) \in V \times V\) (流量限制)
- \(f(u,v)=-f(v,u), \forall (u,v) \in V \times V\)(流量對稱)
- 對於所有\(v \in V \backslash \{s,t\}\),有\(\sum\limits_{u \in V} f(v,u)=0\)(流量守恆)
這個 s-t 流的流量為
\(|f|=\sum\limits_{v \in V} f(s,v)=\sum\limits_{u \in t} f(u,t)\)
這個 s-t 流的費用為
\(W(f)=\sum\limits_{(u,v) \in E} f(u,v)W(u,v)\)
定義
最小費用最大流:流量是最大的情況下,費用最少的流
這個 s-t 流的流量為
\(|f|=\sum\limits_{v \in V} f(s,v)=\sum\limits_{u \in t} f(u,t)\)
這個 s-t 流的費用為
\(W(f)=\sum\limits_{(u,v) \in E} f(u,v)W(u,v)\)
mCMF
Min Cost Max Flow
跟 Ford-Fulkerson 一模一樣!
演算法:
- while \(G_f\) 上有擴充路徑
- 找一條花費最小的路徑擴充
mCMF
Min Cost Max Flow
跟 Ford-Fulkerson 一模一樣!
演算法:
- while \(G_f\) 上有擴充路徑
- 找一條花費最小的路徑擴充
小問題:剩餘流量的花費?
mCMF
Min Cost Max Flow
跟 Ford-Fulkerson 一模一樣!
演算法:
- while \(G_f\) 上有擴充路徑
- 找一條花費最小的路徑擴充
小問題:剩餘流量的花費?
取消花 \(W(u,v)\) 的錢 -> 花 \(-W(u,v)\) 的錢
mCMF
Min Cost Max Flow
mCMF
Min Cost Max Flow
注意到最小花費的路不一定是最短路
所以複雜度退化到 Ford-Fulkerson 的\(O(SP\cdot |f|)\)
其中 SP 為一次最短路要花的時間
因為負邊會憑空跑出來 所以要用 SPFA (很重要)
但是可以證明如果一開始的圖沒有負環,那之後都不會有
CODE
#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll inf = INT64_MAX;
struct edge{
int v, c, r, rid;
ll w;
edge(int _v, int _c, int _r, int _rid, int _w){
v = _v, c = _c, r = _r, rid = _rid, w = _w;
}
};
struct mcmf{
vector<vector<edge>> graph;
vector<int> par, par_eid;
vector<ll> dist;
vector<bool> inq;
mcmf(int n){
graph.resize(n + 1);
dist.resize(n + 1);
par.resize(n + 1);
inq.resize(n + 1);
par_eid.resize(n + 1);
}
void add(int a, int b, int c, ll w){
graph[a].emplace_back(b, c, c, (int)graph[b].size(), w);
graph[b].emplace_back(a, 0, 0, (int)graph[a].size() - 1, -w);
}
bool spfa(int s, int t){
fill(inq.begin(), inq.end(), 0);
fill(dist.begin(), dist.end(), inf);
queue<int> q;
q.emplace(s);
inq[s] = 1;
dist[s] = 0;
while(!q.empty()){
int u = q.front();
q.pop();
inq[u] = 0;
for(int i = 0; i < (int)graph[u].size(); i++){
auto &[v, c, r, rid, w] = graph[u][i];
if(dist[u] + w < dist[v] && r > 0){
dist[v] = dist[u] + w;
par[v] = u;
par_eid[v] = i;
if(!inq[v]) q.push(v), inq[v] = 1;
}
}
}
return dist[t] < inf;
}
pair<ll, ll> flow(int s, int t){
ll ans = 0, mf = 0;
while(spfa(s, t)){
ll cap = inf;
int cur = t;
while(cur != s){
cap = min(cap, (ll)graph[par[cur]][par_eid[cur]].r);
cur = par[cur];
}
cur = t;
while(cur != s){
ans += cap * graph[par[cur]][par_eid[cur]].w;
graph[par[cur]][par_eid[cur]].r -= cap;
graph[cur][graph[par[cur]][par_eid[cur]].rid].r += cap;
cur = par[cur];
}
mf += cap;
}
return make_pair(mf, ans);
}
};
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> n >> m;
mcmf flow(n);
int a, b, c, w;
for(int i = 0; i < m; i++){
cin >> a >> b >> c >> w;
flow.add(a, b, c, w);
}
auto res = flow.flow(1, n);
cout << res.first << " " << res.second << "\n";
}mCMF的酷性質
假設我想找流量為 \(x\) 的最小費用流?
mCMF的酷性質
假設我想找流量為 \(x\) 的最小費用流?
跑 \(x\) 次 SPFA 就好,可以證明是好的
mCMF的酷性質
假設我想找流量為 \(x\) 的最小費用流?
跑 \(x\) 次 SPFA 就好,可以證明是好的
MCMF 時最短路不會變短,跟前面一樣
mCMF的酷性質
假設我想找流量為 \(x\) 的最小費用流?
跑 \(x\) 次 SPFA 就好,可以證明是好的
MCMF 時最短路不會變短,跟前面一樣
假設 \(f(x)\) 為流量為 \(x\) 的最小費用流,\(f(x)\) 會是凸的,
因為 \(f(x+1)-f(x) \geq f(x) - f(x-1)\)
mCMF的酷性質

這個性質後面可以用
例題
可以流但是不能流
例題
XXXXXX
XXXXXXXX
XXXXXX
XXXXXXXXXXXX
- \(1 \leq n \leq 500\)
- \(1 \leq m \leq 1000\)
例題
XXXXXX
XXXXXXXX
XXXXXX
XXXXXXXXXXXX
- \(1 \leq n \leq 500\)
- \(1 \leq m \leq 1000\)
可以建模跑 flow 欸!
例題
XXXXXX
XXXXXXXX
XXXXXX
XXXXXXXXXXXX
- \(1 \leq n \leq\) \(500000\)
- \(1 \leq m \leq\) \(500000\)
我需要解釋
例題
有時候看起來可以 flow
但範圍大到不能 flow
那可能可以用 flow 的一些酷性質導出正解
最大流 = 最小割
有一條路上有 \(n) 個城市
第 \(i\) 個城市出產 \(p_i\) 公斤的產品 最多可以賣 \(s_i\) 公斤的產品
對所有 \(1 \leq i < j \leq n\) 的 \((i,j)\),最多可以從 \(i\) 送 \(c\) 公斤的產品到 \(j\)
問最多能賣多少產品
- \(1 \leq n \leq 10000\)
- \(1 \leq p_i, s_i, c \leq 10^9\)
最大流 = 最小割
最大流 = 最小割
最大流 = 最小割
顯然是最大流..
(自己建模看看)
不能算最大流,那能不能算最小割?
令 \(dp(i,j)\) 為前 \(i\) 個城市中,有 \(j\) 個城市在 \(S\) 中的最小割
轉移:\(dp(i,j)=min(dp(i-1,j-1)+s_i,dp(i-1,j)+p_i+c*j)\)
複雜度 \(O(n^2)\),記得滾動
例題
前情提要:MCMF 的做法大致上有兩種
- 一直找最短路走擴增(前面講的)
- 一直找負環擴增
前情提要:MCMF 的做法大致上有兩種
- 一直找最短路走擴增(前面講的)
- 一直找負環擴增
- 沒負環?從 \(t\) 連一條 cost = \(- \infty\)、cap = \(\infty\) 的邊到 \(s\)
- 找流量為 \(k\) 的最小費用流?cost = \(- \infty\)、cap = \(k\)
前情提要:MCMF 的做法大致上有兩種
- 一直找最短路走擴增(前面講的)
- 一直找負環擴增
- 沒負環?從 \(t\) 連一條 cost = \(- \infty\)、cap = \(\infty\) 的邊到 \(s\)
- 找流量為 \(k\) 的最小費用流?cost = \(- \infty\)、cap = \(k\)
模擬費用流:試著用更快的方法模擬這兩種演算法
例題
poohorz 要辦一場模競,總共有 \(k\) 題
他可以花 \(n\) 天準備,其中第 \(i\) 天可以:
- 花 \(a_i\) 生一題的題目
- 花 \(b_i\) 印一題之前(或今天)生的題目
請問最少需要花多少錢?
- \(1 \leq k \leq n \leq 500000\)
例題
先建模吧

例題
一條擴增路徑一定是:\(s\rightarrow i \rightarrow j \rightarrow t\),而且
- \(s\rightarrow i\) 沒有流
- \(j\rightarrow t\) 沒有流
- \(i \leq j\) 或 ( \(i>j\) 但 \([j,i]\) 都流了至少 \(1\) 流量 )
- 記得可以流回去
例題
一條擴增路徑一定是:\(s\rightarrow i \rightarrow j \rightarrow t\),而且
- \(s\rightarrow i\) 沒有流
- \(j\rightarrow t\) 沒有流
- \(i \leq j\) 或 ( \(i>j\) 但 \([j,i]\) 都流了至少 \(1\) 流量 )
- 記得可以流回去
- 選最小花費的路徑
例題
例題
例題
例題
二分搜一個 \(c\)

例題
考慮從 \(n\) 到 \(1\) 一個一個加點到現在的圖裡面
加了一個點 \(i\) 之後會有兩種負環可以消:
- \(s \rightarrow a_i \rightarrow b_j \rightarrow t \rightarrow s\)
- \(s \rightarrow a_i \rightarrow b_j \rightarrow a_k \rightarrow s\)
例題
考慮從 \(n\) 到 \(1\) 一個一個加點到現在的圖裡面
加了一個點 \(i\) 之後會有兩種負環可以消:
- \(s \rightarrow a_i \rightarrow b_j \rightarrow t \rightarrow s\)
- \(s \rightarrow a_i \rightarrow a_j \rightarrow s\)

例題
考慮從 \(n\) 到 \(1\) 一個一個加點到現在的圖裡面
加了一個點 \(i\) 之後會有兩種負環可以消:
2. \(s \rightarrow a_i \rightarrow b_j \rightarrow a_k \rightarrow s\)

例題
考慮從 \(n\) 到 \(1\) 一個一個加點到現在的圖裡面
加了一個點 \(i\) 之後會有兩種負環可以消:
1. 把 \(a_i\) 跟 \(b_j\) 配
2. 把一對 \((a_k,b_j)\) 幹掉,改成 \((a_i,b_j)\)
事實上還有更多奇怪的負環,但只需要考慮上面這兩種就好,可以證明看看
例題
考慮從 \(n\) 到 \(1\) 一個一個加點到現在的圖裡面
加了一個點 \(i\) 之後會有兩種負環可以消:
- \(s \rightarrow a_i \rightarrow b_j \rightarrow t \rightarrow s\)
- \(s \rightarrow a_i \rightarrow b_j \rightarrow a_k \rightarrow s\)
開一個 pq 存目前可能被配的東西
每次 pop 最小的配 (如果加起來小於0)
配完要把可能跟別人配的 push 進去:
- 如果 \(a_i\) 配走,那要 push \(-a_i\)
- 如果 \(b_i\) 沒被配,那要 push \(b_i-c\)
例題
習題
習題
今天沒有講的東西
- 全域最小割
- Stoer-Wagner
- Karger
- 最小割樹 (Gomory-Hu Tree)
- 上下界流
- 其他我不知道的東西