暑訓教學
組合賽局

講師介紹
賽局理論
(Game Theory)
策略
- 策略,或稱戰略,是決定及實行基本和長期目標及目的的過程,或是為了實現目標所需資源的配置行為。
- 在賽局理論中,我們定義的策略即為某個實體根據目前所擁有的資訊,對達成目標的一切思考及行動。
- 其中,最佳化策略即為客觀認為最能有效達成目標的一種策略。
分類
靜態 vs 動態
零合 vs 非零合
組合賽局
What is 組合賽局 ?
- 兩位玩家輪流進行操作
- 賽局盤面資訊完全公開
- 任何盤面下的任何操作皆不含機率成分
- 賽局結果存在三一律,A勝B敗、B勝A敗、AB平手
勝利失敗條件
勝利條件:
現在這個盤面為必勝:可以轉移到一個對手必敗的盤面。
失敗條件:
現在這個盤面為必敗:可以轉移到的任何盤面對手都必勝。



























Zermelo's theorem
對於一個組合賽局,以下三者必有一成立。
1.先手擁有必勝策略
2.後手擁有必勝策略
3.兩人都有平手策略
一些組合賽局分類
- 標準 vs 匱乏
- 有偏 vs 無偏
賽局經典遊戲
囚徒困境
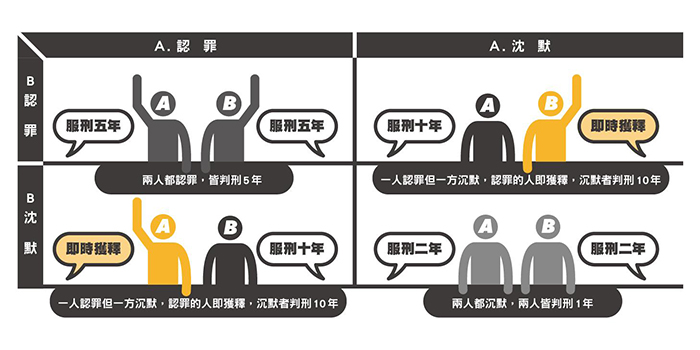
小遊戲
濕婆神與雪山神女
傳聞濕婆神曾經與他的配偶雪山神女來到喜馬拉雅山下的小村莊摩耶拉赫,當地在秋天的豐收節總會玩一個簡單的小遊戲,他們會在毗濕奴神廟前擺上21顆山竹,並讓村裡最賢能的一男一女輪流拿取1~3顆山竹,拿到最後一顆山竹的就能成為當年度的長老,若您正在與濕婆神對戰,該選擇先拿還是後拿呢?
賽拉耶佛風土記
道光十三年春,同友人遊波士尼亞,於逆旅榻座數日,望東市尋湯餅,途上覘土民遊戲於江岸,某吏疊數十幣列於几上,令二翁相互取幣遊戲,每每皆取二之冪次者,取末者勝,嚐驚奇,以此境之異聞為之妙。
邊緣鴨嘴獸寶寶
密西西比河上游有奇數隻鴨嘴獸寶寶,他們總是成雙成對的游泳,並留下一隻落單,你與另一位拓荒探險家皆想把他們抓回家當寵物,你們可以輪流抓取,每次選擇拿1隻或是2隻鴨嘴獸,但邪惡的杜芬舒斯博士發明了鴨嘴獸終結者,每觀察到一對不在密西西比河上游的鴨嘴獸就會把他們做成蔥燒麻辣鴨嘴獸,為此你期望拿到奇數隻鴨嘴獸,這樣就能留下最後一隻成為你的寵物,也就是最邊緣的那一隻。
波提切利叔叔的薯條
波提切利叔叔是一個在聖彼得堡的薯條小販,由於波提切利叔叔小時候遭遇的種種不幸,他十分喜歡與顧客玩一個刺激的小遊戲,波提切利叔叔會準備兩盤薯條,並與一位顧客輪流吃薯條,但是他們每次吃薯條的方法有特別的限制,那就是每次選擇吃一盤當中任意數量的薯條,並在另外一盤中選擇要吃與前一盤相同數量的薯條或是都不吃,吃到最後一根薯條的玩家獲勝。
格物樓地下室邊緣人
某個邊緣人喜歡在地下室到處找人喝酒賭博(沒錯,建中的地下室文化就是這麼可悲),他尤其喜歡玩一個遊戲,每次會有好幾堆硬幣,兩個人輪流操作,每次一個人可以從任意一堆拿至少一個硬幣,拿到最後一個硬幣的人就能拿走全部的硬幣,你要怎麼拿到最後一個硬幣呢? 先不用考慮酒精對你的腦袋的影響,以後再說。
怎麼有些人這麼強?
濕婆神與雪山神女
這個遊戲與初始數字有很大的關係:
初始數字是\(4\)的倍數的話是後手必勝,不然就是先手必勝!
策略:
如果現在是\(4\)的倍數,先手拿\(k\)個,後手就拿\(4-k\)個,拿到最後一個的一定是後手!
只要想辦法把現在的數字變成\(4\)的倍數就好了!
另一方毫無反制之力!
這樣就很明顯了吧!
賽拉耶佛風土記
有沒有聯想到二進位?
完全無關!
初始數字為\(3\)的倍數是後手勝,
否則是先手勝!
策略:跟前一題很像,但你會發現所有\(2^k\)的數字除以\(3\)都會餘\(1\)或\(2\),所以如果當前剩餘數量是\(3\)的倍數,一方怎麼取,另一方都可以把它取回\(3\)的倍數,就能輕鬆得勝!
很簡單吧!
可以拿去騙騙人!
邊緣鴨嘴獸寶寶
前言:
這題的勝利策略已經不像前面那麼顯然,講師如果用大腦跟你玩也不一定得會贏
但不一定要用人腦......
我們是資訊社欸!
(接下來的東西如果覺得有點困難、聽不懂、想睡覺、覺得講師不知道在幹嘛......完全沒有關係,很正常,有興趣、聽得懂的人就聽,也可以再找我討論)
還記得前面講的勝利失敗條件嗎?
畫圖分析!
講師要用小畫家講課笑死
可以用程式跑!
實際細節可能有機會再說吧!
附code
大家看看就好
int dp[105][2][2];
void eval(){
for(int i=0;i<100;i++){
if(dp[i][0][0]==-1) dp[i][0][0]=0;
if(dp[i][0][1]==-1) dp[i][0][1]=0;
if(dp[i][1][0]==-1) dp[i][1][0]=0;
if(dp[i][1][1]==-1) dp[i][1][1]=0;
if(dp[i][0][0]==0){
dp[i+1][1][0]=1;
dp[i+2][0][0]=1;
}
if(dp[i][0][1]==0){
dp[i+1][0][0]=1;
dp[i+2][1][0]=1;
}
if(dp[i][1][0]==0){
dp[i+1][1][1]=1;
dp[i+2][0][1]=1;
}
if(dp[i][1][1]==0){
dp[i+1][0][1]=1;
dp[i+2][1][1]=1;
}
}
}格物樓地下室邊緣人
這其實是經典的標準無偏賽局:Nim!
數學家發展了一套分析標準無偏賽局的理論,使用Sprange-Grundy Value,或稱SG Value, nimber, nimsum等等
另外,Sprange-Grundy Theorem表明每一個標準無偏賽局都可以對應到某一種數量的Nim,是標準無偏賽局的終極大定理,以後有機會再聊吧!
Nim的先手必勝條件:將每一堆的數量XOR起來,若此值為0則後手必勝,否則先手必勝。
甚麼是XOR?
將數字以二進位表示,兩個數字的每一位相異則\(1\),否則\(0\)
為什麼?
首先,全部拿完的盤面XOR的值是0
然後我們可以構造出一種方法,使得是0的盤面一定只能變成非0,非0的盤面一定可以變成0。
所以就是好的!
講義中有做法,大家可以參考看看!
Huh?
是不是跟之前的取到3、4的倍數很像?
沒有錯!