Random Forest
Stéphane Yanan
Yves Legris
Le 20 Novembre 2016

Plan
- Contexte de l'étude
- Le problème posé en terme de fouille de données ainsi que les objectifs visés
- La structure de donnée
- Données d'apprentissages et de tests
- Description de l'algorithme
- L'analyse comparative
- Résultats obtenus
- Conclusion
1. Contexte de l'étude
Méthode introduite par Leo Breiman en 2001
Idées plus anciennes : Bagging (1996), arbres dedécisions CART (1984)

Preuves de convergences récentes (2006, 2008)
Historique & référence
Les forêts aléatoires consistent à faire tourner en parallèle un grand nombre d’arbres de décisions construits aléatoirement, avant de les moyenner.
Une forêt (Forest)= un ensemble d'arbres
Aléatoire (Random) = Choix au hasard d'un sous arbre
1. Contexte de l'étude
En termes statistiques, si les arbres sont décorrélés, cela permet de réduire la variance des prévisions.
Explication


Bagging ou Random Forests : utiliser le hasard pour améliorer les performances d’algorithmes de «faibles» performances. C’est applicable à différents algorithmes et RF est un aménagement spécifique à CART.
1. Contexte de l'étude
Explication
3 choses importantes concernant Random Forest :
Out Of Bag (OOB) estimate error
Le nombre d'arbre (number of trees)
Le nombre de variable testés à chaque division (mtry)
Le but du jeu est d’obtenir l’OOB le plus petit possible. Pour minimiser cette valeur, on peut régler deux éléments : le nombre d’arbres construits par l’algorithme (ntree) et le nombre de variables testées à chaque division (mtry).
1. Contexte de l'étude
Explication
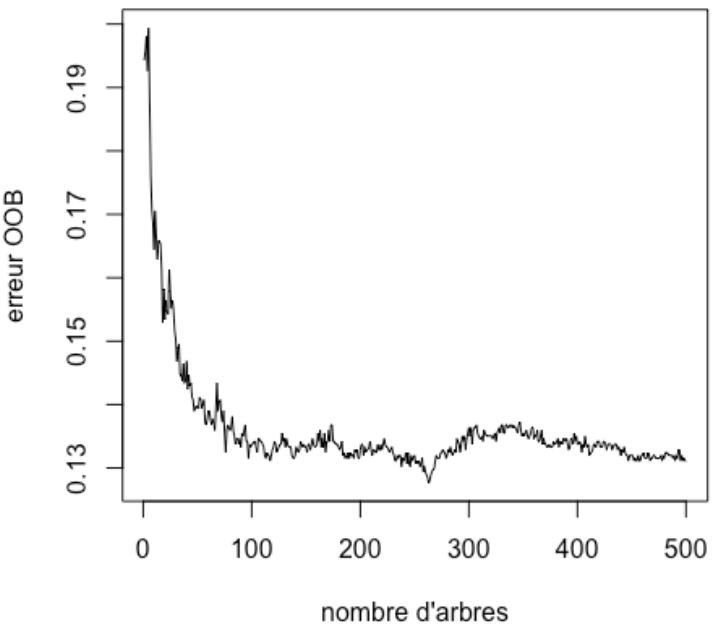
Ici, on voit que plus le nombre d'arbre est grand, plus l'OOB diminue
2. Objectifs visés
Performant pour la prédiction
Objectif : obtenir des arbres les plus décorrélés possible, de façon à ce qu'ils soient indépendants
A utiliser lors d'un grand nombre de variable explicative, ou dans les grandes dimensions (ex : bio-puces, signaux, images ...)



2. Problèmes rencontrés
Ne pas utiliser pour implémenter des règles de décision
Effet boite noire, comme pour les réseaux de neuronnes


3. Structure de donnée utilisée
Ensemble de données choisi : IRIS
150 exemples de critères observé sur 3 espèces différentes
Chaque exemple est composé de 4 attributs

Fichier iris.arff
@ATTRIBUTE sepallength REAL
@ATTRIBUTE sepalwidth REAL
@ATTRIBUTE petallength REAL
@ATTRIBUTE petalwidth REAL
@ATTRIBUTE class {Iris-setosa,Iris-versicolor,Iris-virginica}3. Données d'apprentissages et de tests
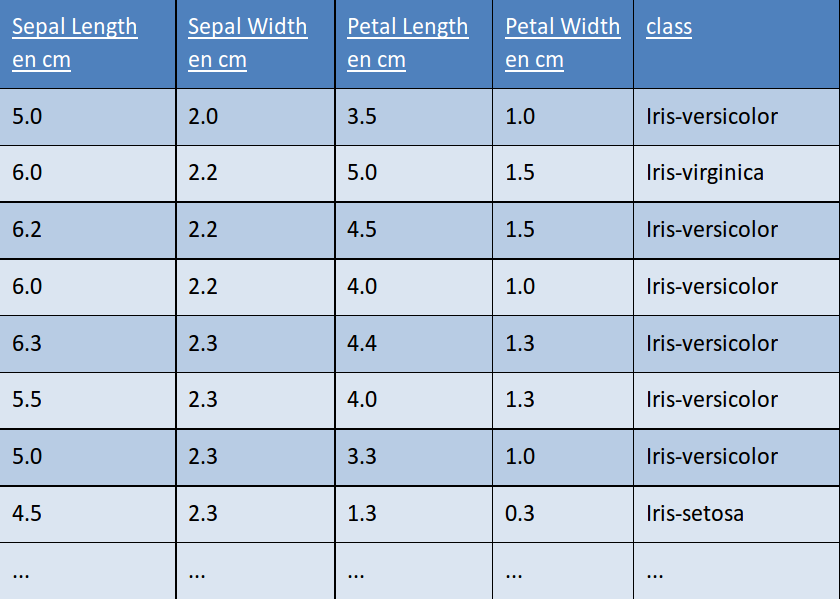
Échantillon de donnée d'apprentissage
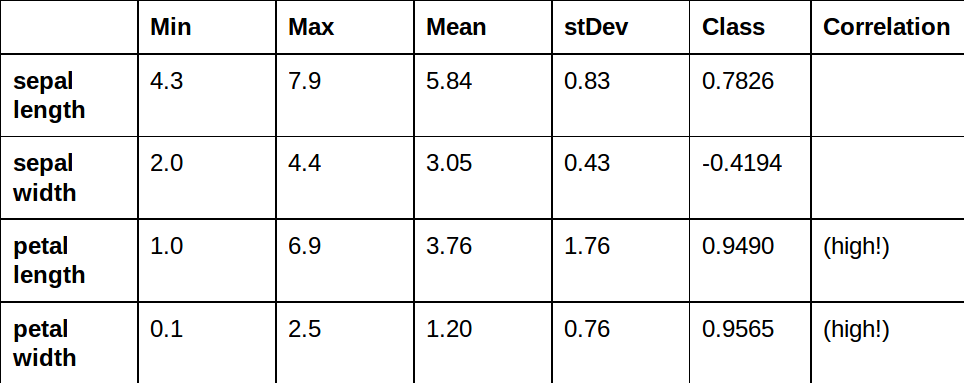
Statistique de nos valeurs


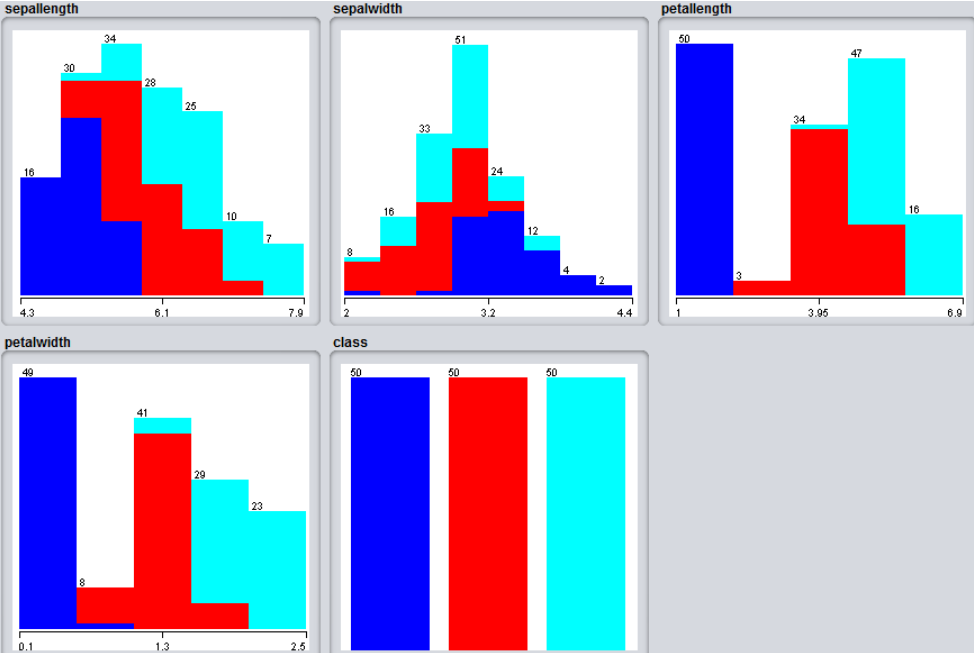
3 espèces différentes :
Setosa (en bleu)
Versicolor (en rouge)
Virginica (en turquoise)
Cross-validation : 10

3. Données d'apprentissages et de tests
3. Données d'apprentissages et de tests

Résultat obtenu

Temps : 0.07 secondes - Taux d'erreur : 4.67% (7)
3. Données d'apprentissages et de tests

La moyenne des True Positive, correspond au positive correctement prédit, est de 0.953
La moyenne des False Positive, correspond au négative prédit à tort comme des classes positives est de 0.023
La Precision est de 0.953, (c’est une détermination de l’exactitude, c’est le rapport des cas positifs prédits qui étaient exacts au nombre total de cas positifs prédits).
Détails par classe

3. Description détaillée de l'algorithme
ArbreDecision(T)
si "condition d'arret"
retourner feuille(T)
sinon
choisir le "meilleur" attribut parmi un sous ensemble choisi aléatoirement
pour chaque valeur v de l'attribut i
T[v] = {(x, y) de T tels que x_i = v}
t[v] = ArbreDecision(T[v])
fin pour
retourner noeud(i, {v -> t[v]})
fin siÉchantillonage des attributs :
On tire uniformément au hasard un sous-ensemble A′ ⊂ A de taille m′ ≤ m (pour la régression, les auteurs suggèrent m′ ≈ m/3) dont on choisira le meilleur attribut. L’objectif de cette opération est de décorréler les arbres produits, la corrélation entre les prédicteurs réduisant les gains potentiels en précision dus au bagging.
Critère d’arrêt :
Les arbres construits sont aussi profonds que possible, i.e. le critère d’arrêt est une condition forte (|Tf| < 10, | Yf| = 1, ...), dans les limites d’un temps de calcul raisonnable. Ainsi, un prédicteur apprendra toutes les relations entre les données à sa portée, le surapprentissage et la sensibilité au bruit qui en résultent étant compensés par le bagging.
1
1
2
2
4. Analyse Comparative
Comparaison avec l'algorithme J48
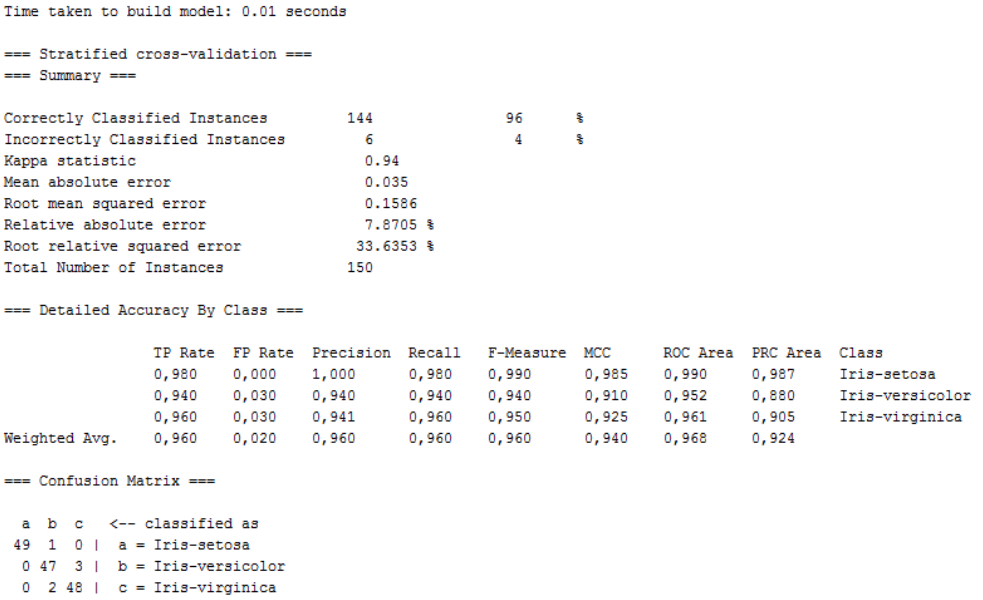
Temps : 0.01 secondes - Taux d'erreur : 4% (6)
Résultat obtenu

5. Résultats obtenus

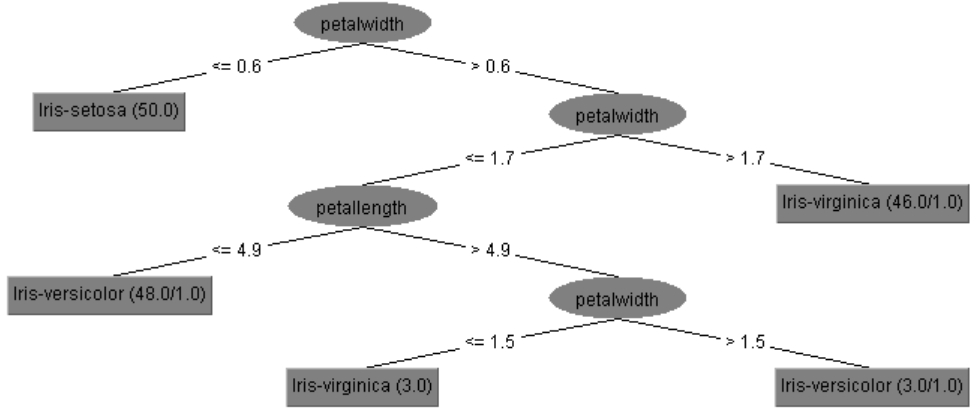
6. Conclusion
Les résultats montrent que l'algorithme Random Forest prend plus de temps pour classer les données et nous donne moins de précision.
L’algorithme J48 nous offre une meilleure précision avec une légère augmentation du temps pour la classification.
Le taux d’erreur est plus élevé avec l’algorithme RandomForest comparer à J48.
De plus l’algorithme J48 nous donne la possibilité de générer un arbre ce qui n’est pas possible avec le RandomForest sous l'environnement Weka.