Fearless programming and reasoning with infinities

Alexander Gryzlov

IMDEA Software Institute

06/06/2024

Agenda

  • Totality, partiality and fixed points
  • Infinite data
  • Interfaces and objects
  • Automata
  • Extra ideas & conclusions

Part 1

purely functional programming

=

programming and reasoning with

referentially transparent

higher-order functions

 

Having explicit effects simplifies

reasoning and formalization

Totality, partiality and fixed points

Purity

Very useful for reasoning about

intention and correctness

 

Types classify well-behaved programs,

but we inevitably lose some

 

So there's a quest to regain expressivity by

making type system more powerful

 

Allow more communication between

types and programs!

Totality

Pushing type-based reasoning further gives

dependent types

We can program the type-checker itself and build structures with invariants

data Vec (A : 𝒰 ℓ) : ℕ → 𝒰 ℓ where
  []  : Vec A zero
  _∷_ : A → Vec A n → Vec A (suc n)

Totality

data Format = Number Format | Str Format
            | Lit String Format | End

PrintfType : Format → 𝒰
PrintfType (Number fmt) = (i : Int) → PrintfType fmt
PrintfType (Str fmt) = (str : String) → PrintfType fmt
PrintfType (Lit str fmt) = PrintfType fmt
PrintfType End = String

printfFmt : (fmt : Format) → (acc : String) → PrintfType fmt
printfFmt (Number fmt) acc = λ i → printfFmt fmt (acc ++ show i)
printfFmt (Str fmt) acc = λ str → printfFmt fmt (acc ++ str)
printfFmt (Lit lit fmt) acc = printfFmt fmt (acc ++ lit)
printfFmt End acc = acc

toFormat : (xs : List Char) → Format
toFormat [] = End
toFormat ('%' :: 'd' :: chars) = Number (toFormat chars)
toFormat ('%' :: 's' :: chars) = Str (toFormat chars)
toFormat ('%' :: chars) = Lit "%" (toFormat chars)
toFormat (c :: chars) = case toFormat chars of
                             Lit lit chars' => Lit (strCons c lit) chars'
                             fmt => Lit (strCons c "") fmt

printf : (fmt : String) -> PrintfType (toFormat (unpack fmt))
printf fmt = printfFmt _ ""

Totality

This however means that purity is not enough

Functions have to be total: defined everywhere

Otherwise the type-checking crashes or fails

= inconsistent logic

{-# TERMINATING #-}
void : ⊥
void = void

oops : 2 + 2 ＝ 5
oops = absurd void

Safety and liveness

Correctness properties typically split into

  • safety (nothing bad ever happens)
  • liveness (something good eventually happens)

 

Totality also has two aspects:

  • defined input (no crashing)
  • producing output (no hanging)

Safety & liveness reasoning

Partial functions violating safety

=

some arguments are not handled

Typically handled by either restricting the domain

or wrapping codomain in Maybe/Either

 

Violation of liveness = non-termination

We need to reason about unfolding computations

Non-termination

Temporal aspects are typically "invisible"

How to model endless computation?

 

Total programming usually restricts to

terminating functions

Too narrow, cannot reason about interactive programs

Need to model control flow in the type system

Non-termination hacks

We can try adding hacks:

  1. construct individual terminating steps
  2. make a small unsafe function that spins the steps
  3. alternatively, add number of steps and then unsafely generate an infinite number
data Fuel = Dry | More Fuel

limit : ℕ → Fuel
limit  zero   = Dry
limit (suc n) = More (limit n)

{-# TERMINATING #-}
forever : Fuel
forever = More forever

There should be a fully formal solution

Type-level time

A natural way of reasoning about time is to split it into steps/ticks on some global clock

The flow of time should be unidirectional

...

A thunk calculus

  • Add a special type constructor ▷
  • ▷A is "A, but available one step later"
  • Essentially a type-level thunk () ⇒ A
  • Can also be thought of as staging (to run in the next stage)
  • The program generates a new program that runs after the first one and so on

...

▷

▷▷

▷▷▷

Structure of later

It's an applicative functor

(will write ap as ⊛) 

next : A → ▷A
ap : ▷(A → B) → ▷A → ▷B

Functorial structure

  • We can derive a functorial action (will write map as ⍉)
  • All the laws hold definitionally (by symbolic computation)
map : (A → B) → ▹ A → ▹ B
map f a▹ = next f ⊛ a▹
ap-map : (f : A → B) → (x▹ : ▹ A)
       → (next f ⊛ x▹) ＝ f ⍉ x▹
ap-map f x▹ = refl

Not a monad

There is no monadic structure

 

flatten : ▹ ▹ A → ▹ A

This ensures that the temporal structure is preserved

▷

For an arbitrary type there's also typically no

▹ A → A

(though we can do it for universes)

Guarded recursion

  • We can schedule computations, what now?
  • Terminating → Productive recursive programs
  • Every recursive call is "guarded" by a thunk, returning control
  • Infinite / streaming computations, servers, OSs

...

▷

▷▷

▷▷▷

Guarded recursion

  • A form of Y-combinator
  • Postulated definition, unfolding made propositional
  • Can be erased into a general recursive fixpoint
fix: (▹ A → A) → A
postulate
  dfix : (▹ A → A) → ▹ A
  pfix : (f : ▹ A → A) → dfix f ＝ next (f (dfix f))

fix : (▹ A → A) → A
fix f = f (dfix f)

fix-path : (f : ▹ A → A) → fix f ＝ f (next (fix f))
fix-path f i = f (pfix f i)

Ticked type theory

  • We'll use Agda proof assistant for interactive examples
  • Guarded modality is encoded as a function from a modal Tick: 𝕋
  • A tick is a proof of an elapsed time step
  • Can encode next, ap and map

  • Black triangle ▸ is a type-level time shift

▹_ : 𝒰 ℓ → 𝒰 ℓ
▹_ A = (@tick α : Tick) → A

▸_ : ▹ 𝒰 ℓ → 𝒰 ℓ
▸ A▹ = (@tick α : Tick) → A▹ α

Ticked cubical type theory

  • Technically we're using the cubical mode of Agda
  • Equality is encoded as a function from a continuous interval type 𝕀
  • The interval is allowed to commute with the tick ("time-travel")
  • Allows to reason about the future in the present
▹-ext : {A : 𝒰 ℓ} {x▹ y▹ : ▹ A}
      → ▹[ α ] (x▹ α ＝ y▹ α)
      → x▹ ＝ y▹
▹-ext p i α = p α i 

▹-iso : x▹ ＝ y▹ ≅ (▹[ α ] (x▹ α ＝ y▹ α))

Logical justification

  • A flavour of provability modality
  • 1933 - Gödel's analysis of S4
  • 1950s - (Weak) Löb's axiom:   □(□A → A) → □A

  • We're using the strong version: (□A → A) → A

  • 1960s - GL system
  • 1970s - intuitionistic systems, fixed points
  • 2000s - links to formal semantics and category theory

Nakano's approximation

  • Nakano, [2000] "A modality for recursion"
  • ▷was initially written ⏺
  • Continued by many authors, most notably:
    Atkey-McBride'13
  • A series of papers by Birkedal and coauthors in 2010s
  • Viewed as a special type constructor in the type system

Programming with ▷

So, to recap we have essentially 4 new constructs:

 

▷, next, ap/⊛, fix

 

(+ ▸, map/⍉ and some proof machinery)

What can we write with these?

Part 2

Which infinite types make sense?

Infinite data

Fitting the fix

Previously, I've said that for an arbitrary type there typically is no

▹ A → A

However, that is the type of function we need:

 

 

We can construct such types with ▹

fix: (▹ A → A) → A

Partiality effect

  • Recall the motivation of having a non-termination effect
  • We can express it with 2 constructors + a guard annotation
  • Many names: L(ift), Event, Delay 
data Part (A : 𝒰) : 𝒰 where
  now   : A → Part A
  later : ▹ Part A → Part A

...

Partiality functor

Mapping a function = waiting until the end and applying it

map-body : (A → B) 
         → ▹ (Part A → Part B)
         →    Part A → Part B
map-body f m▹ (now a)   = now (f a)
map-body f m▹ (later p) = later (m▹ ⊛ p)

map : (A → B) → Part A → Part B
map f = fix (map-body f)

...

...

Partiality applicative

Unwind both structures "in parallel"

pure : A → Part A
pure = now

ap-body : ▹ (Part (A → B) → Part A → Part B)
          →  Part (A → B) → Part A → Part B
ap-body a▹ (now f)    (now x)    = now (f x)
ap-body a▹ (now f)    (later x▹) = later (a▹ ⊛ next (now f) ⊛ x▹)
ap-body a▹ (later f▹) (now x)    = later (a▹ ⊛ f▹ ⊛ next (now x))
ap-body a▹ (later f▹) (later x▹) = later (a▹ ⊛ f▹ ⊛ x▹)

ap : Part (A → B) → Part A → Part B
ap = fix ap-body

...

...

...

Partiality monad

  • Essentially an arbitrary sequence of nested ▹'s

  • Reassociating makes it a monad (▹▹▹(▹▹A) → ▹▹▹▹▹A)

flatten-body : ▹ (Part (Part A) → Part A)
             →   Part (Part A) → Part A
flatten-body f▹ (now p)    = p
flatten-body f▹ (later p▹) = later (f▹ ⊛ p▹)

flatten : Part (Part A) → Part A
flatten = fix flatten-body

...

...

Partiality effect

never : Part ⊥
never = fix later

collatz-body : ▹ (ℕ → Part ⊤) → ℕ → Part ⊤
collatz-body c▹ 1 = now tt
collatz-body c▹ n =
  if even n then later (c▹ ⊛ next (n ÷2))
            else later (c▹ ⊛ next (suc (3 · n)))

collatz : ℕ → Part ⊤
collatz = fix collatz-body

Wraps potentially non-terminating computations

Indexed partiality monad

Complexity can be made explicit by

indexing with steps

data Delayed (A : 𝒰) : ℕ → 𝒰 where
  nowD   : A → Delayed A zero
  laterD : ∀ {n} → ▹ (Delayed A n) → Delayed A (suc n)

Cannot express infinite computations anymore:

there's no ▹ (Delayed A n) → Delayed A n

Indexed partiality monad

Can be made more explicit by indexing with steps

mapᵈ : (A → B) → Delayed A n → Delayed B n

apᵈ : Delayed (A → B) m
    → Delayed A n 
    → Delayed B (max m n)

runs sequentially

Encoding applicative via bind changes complexity!

_>>=ᵈ_ : Delayed A m 
       → (A → Delayed B n) 
       → Delayed B (m + n)

runs "in parallel"

Conaturals

Unary numbers extended with numerical infinity

≅ Part⊤

data ℕ∞ : 𝒰 where
  ze : ℕ∞
  su : ▹ ℕ∞ → ℕ∞
  
infty : ℕ∞
infty = fix su

+-body : ▹ (ℕ∞ → ℕ∞ → ℕ∞) → ℕ∞ → ℕ∞ → ℕ∞
+-body a▹    ze        ze     = ze
+-body a▹ x@(su _)     ze     = x
+-body a▹    ze     y@(su _)  = y
+-body a▹   (su x▹)   (su y▹) = 
      su (next (su (a▹ ⊛ x▹ ⊛ y▹)))

_+_ : ℕ∞ → ℕ∞ → ℕ∞
_+_ = fix +-body

Conatural subtraction

∸-body : ▹ (ℕ∞ → ℕ∞ → Part ℕ∞) 
       →    ℕ∞ → ℕ∞ → Part ℕ∞
∸-body s▹    ze      _      = now ze
∸-body s▹ x@(su _)   ze     = now x
∸-body s▹   (su x▹) (su y▹) = later (s▹ ⊛ x▹ ⊛ y▹)

_∸_ : ℕ∞ → ℕ∞ → Part ℕ∞
_∸_ = fix ∸-body

(Saturating) subtraction is partial:

∞ ∸ ∞ never terminates

Conatural proof

∸ᶜ-infty : infty ∸ᶜ infty ＝ never
∸ᶜ-infty = fix λ cih▹ →
  infty ∸ᶜ infty
    ~⟨ ... unroll subtraction and infinity definitions with fix-path ... ⟩
  later ((next _∸ᶜ_) ⊛ next infty ⊛ next infty)
    ~⟨⟩
  later (next (infty ∸ᶜ infty))
    ~⟨ ap later (▹-ext cih▹) ⟩
  later (next never)
    ~⟨ fix-path later ⁻¹ ⟩
  never
    ∎

Proofs typically follow this pattern:

  1. unroll fixed points by a necessary amount of steps
  2. apply equations + "coinductive hypothesis"
  3. roll fixed points back

Co/free monad

Partiality is just an instantiation of the free monad with the  ▷  functor

  • Free monad is an F-branching tree with data on the leaves
  • Cofree comonad is a tree with data at the branches
  • What do we get by instantiating Cofree with ▷ ?

 

data Free (F : 𝒰 → 𝒰) (A : 𝒰) : 𝒰 where
  Pure : A → Free F A
  Roll : F (Free F A) → Free F A

data Cofree (F : 𝒰 → 𝒰) (A : 𝒰) : 𝒰 where
  Cof : A → F (Cofree F A) → Cofree F A

Streams

  • Another classical infinite structure
  • An inductive list with a delayed tail and no empty case
  • A lazy linear producer of values
data Stream (A : 𝒰) : 𝒰 where
  cons : A → ▹ Stream A → Stream A

...

Stream functions

headˢ : Stream A → A
headˢ (cons x _) = x

tail▹ˢ : Stream A → ▹ Stream A
tail▹ˢ (cons _ xs▹) = xs▹

repeatˢ : A → Stream A
repeatˢ a = fix (cons a)

mapˢ-body : (A → B) 
          → ▹ (Stream A → Stream B) 
          →    Stream A → Stream B
mapˢ-body f m▹ as = cons (f (headˢ as)) (m▹ ⊛ (tail▹ˢ as))

mapˢ : (A → B) → Stream A → Stream B
mapˢ f = fix (mapˢ-body f)

natsˢ-body : ▹ Stream ℕ → Stream ℕ
natsˢ-body n▹ = cons 0 (mapˢ suc ⍉ n▹)

natsˢ : Stream ℕ
natsˢ = fix natsˢ-body

Stream comonad

extract = head

duplicate = tails

extractˢ : Stream A → A
extractˢ = headˢ

duplicateˢ-body : ▹ (Stream A → Stream (Stream A)) 
                →    Stream A → Stream (Stream A)
duplicateˢ-body d▹ s@(cons _ t▹) = cons s (d▹ ⊛ t▹)

duplicateˢ : Stream A → Stream (Stream A)
duplicateˢ = fix duplicateˢ-body

...

...

...

...

...

Causality

  • We can define stutter but not everyother
  • Violates casualty
  • (can be defined with clocks, however)
stutter : Stream A → Stream A
stutter = fix λ d▹ s → 
  cons (headˢ s) (next (cons (headˢ s) (d▹ ⊛ tail▹ˢ s)))

-- everyother : Stream A → Stream A
-- everyother = fix λ e▹ s → 
--   cons (headˢ s) (e▹ ⊛ tail▹ˢ (tail▹ˢ s {!!}))

...

Folds and numbers

  • We can define other familiar functions
  • foldr, scan, zipWith, interleave
  • numerical streams
fibˢ-body : ▹ Stream ℕ → Stream ℕ
fibˢ-body f▹ = 
  cons 0 ((λ s → cons 1 $ (zipWithˢ _+_ s) ⍉ (tail▹ˢ s)) ⍉ f▹)

fibˢ : Stream ℕ
fibˢ = fix fibˢ-body

primesˢ-body : ▹ Stream ℕ → Stream ℕ
primesˢ-body p▹ = cons 2 ((mapˢ suc ∘ scanl1ˢ _·_) ⍉ p▹)

primesˢ : Stream ℕ
primesˢ = fix primesˢ-body

Part 3

Let's look at the definition of the stream again

Objects and interfaces

A datatype with a single constructor is essentially a record

data Stream (A : 𝒰) : 𝒰 where
  cons : A → ▹ Stream A → Stream A

Iterator

We can treat the stream as an iterator object with two methods:

  1. reading the head value
  2. advancing by one step
record Stream (A : 𝒰) : 𝒰 where
  constructor cons
  field
    hd  : A
    tl▹ : ▹ Stream A

Branching iterator

Can be generalized to an infinite binary tree

data Tree∞ (A : 𝒰) : 𝒰 where
  node : A → ▹ Tree∞ A → ▹ Tree∞ A
       → Tree∞ A

record Tree∞ (A : 𝒰) : 𝒰 where
  constructor node
  field
    val : A
    l▹  : ▹ Tree∞ A
    r▹  : ▹ Tree∞ A

...

Branching iterator

Or a rose tree with arbitrary branching

data RTree (A : 𝒰) : 𝒰 where
  rnode : A → List (▹ RTree A) → RTree A

record RTree (A : 𝒰) : 𝒰 where
  constructor rnode
  field
    val : A
    ch▹ : List (▹ RTree A)

...

Terminating iterators

Multiple constructors makes this harder

data Colist (A : 𝒰) : 𝒰 where
  cnil  : Colist A
  ccons : A → ▹ Colist A → Colist A

record Colist0 (A : 𝒰) : 𝒰 where
  constructor ccons0
  field
    hd  : Maybe A
    tl▹ : ▹ Colist0 A
    
record Colist1 (A : 𝒰) : 𝒰 where
  constructor ccons1
  field
    hd   : A
    emp? : Bool    
    tl▹  : ▹ Colist1 A

Set interface

How would we represent an infinite set of ℕ?

(a finite set is usually some search structure RedBlackTree ℕ)

 

Typically via a function ℕ → Prop/Bool

We can also use Stream Bool

Generally, Stream A ≅   ℕ → A

Tabulation of a function

However, this is not very efficient

...

1

2

3

1

0

Set interface

Instead, we can encode a set interface as

a recursive guarded record

(actual implementation a bit more technical)

record Setℕ : 𝒰 where
  constructor mkSet
  field
    emp? : Bool
    has? : ℕ → Bool
    ins  : ℕ → ▹ Setℕ
    uni  : ▹ Setℕ → Part Setℕ

Strict positivity

  • Guarded recursion has two general areas of application:
  1. Working with potentially infinite data structures
  2. Encoding non-strictly-positive recursive types

 

  • Strictly positive type appears to the left of 0 arrows
  • A syntactic approximation of monotonicity

Strict positivity

  • Strictly positive type appears to the left of 0 arrows
  • Another syntactic approximation
  • Positive type appears in even positions
  • Negative type appears in odd positions
data Expr : 𝒰 → 𝒰 where 
  Foo : ((Expr a → Expr a) → Expr b) → Expr (a → b) 
          ^^^^^^----------------------- positive occurrence
                   ^^^^^^-------------- negative occurrence 
                             ^^^^^^---- strictly positive occurrence

A finite set object

finiteSet-body : ▹ (List ℕ → Setℕ) 
               →   List ℕ → Setℕ
finiteSet-body f▹ l =
  mkSet (empty? l)
        (λ n → elem? n l)
        (λ n → f▹ ⊛ next (n ∷ l))
        (λ x▹ → later ((λ x →
           foldrP (λ n z →
              later (now ⍉ (z .ins n))) x l) ⍉ x▹))

finiteSet : List ℕ → Setℕ
finiteSet = fix finiteSet-body

Carries around the search structure (here a List)

An infinite set object

evensUnion-body : ▹ (Setℕ → Setℕ) 
                →    Setℕ → Setℕ
evensUnion-body e▹ s =
  mkSet false
        (λ n → even n or s .has? n)
        (λ n → e▹ ⊛ s .ins n)
        (λ x▹ → later ((λ f →
           mapᵖ f (s .uni x▹)) ⍉ e▹))

evensUnion : Setℕ → Setℕ
evensUnion = fix evensUnion-body

Delegates to the parameter

Objects with IO

This idea can be extended to state and effects

Encode IO as a form of a partiality monad and

abstract over methods using polynomials

record IOTree : 𝒰 (ℓsuc 0ℓ) where
  field
    Command : 𝒰
    Response : Command → 𝒰

data IOProg (I : IOTree) (A : 𝒰) : 𝒰 where
  ret : (a : A) → IOProg I A
  bnd : (c : Command I) (f : Response I c → ▹ IOProg I A) → IOProg I A

record Interface : 𝒰 (ℓsuc 0ℓ) where
  field
    Method : 𝒰
    Result : Method → 𝒰

record IOObj (Io : IOTree) (I : Interface) : 𝒰 where
  field
    mth : (m : Method I) → IOProg Io (Result I m × IOObj Io I)

Part 4

Let's go back to the idea of function tabulation

Stream A ≅   ℕ → A

What is the infinite tree isomorphic to?

Automata

data Tree∞ (A : 𝒰) : 𝒰 where
  node : A → ▹ Tree∞ A → ▹ Tree∞ A
       → Tree∞ A

Word consumers

Tree∞ A ≅   ℕ₂ → A

(the type of binary numbers)

There's general construction to tabulate

T → A into some F A

where the structure of F mirrors that of T

...

1

10

11

101

100

110

111

Tries

We can think of structures as infinite tries whose branching factor is determined by T

...

Word automata

This idea can be generalized even further, to tabulated polymorphic functions:

data Stream (A : 𝒰) : 𝒰 where
  cons : A → (⊤ → ▹ Stream A) → Stream A

data Tree∞ (A : 𝒰) : 𝒰 where
  cons : A → (Bool → ▹ Tree∞ A) → Tree∞ A

data Moore (X A : 𝒰) : 𝒰 where
  mre : A → (X → ▹ Moore X A) → Moore X A

Word automata

Moore X A ≅ List X → A

Deterministic Moore automaton, common special case is

Moore X Bool ≅ List X → Bool

which is typically called a recognizer

data Moore (X A : 𝒰) : 𝒰 where
  mre : A → (X → ▹ Moore X A) → Moore X A

Operations on automata

pure : B → Moore A B
pure b = fix (pure-body b)

map : (B → C)
    → Moore A B → Moore A C
...

ap : Moore A (B → C) → Moore A B → Moore A C
..

zipWith : (B → C → D) 
        → Moore A B → Moore A C → gMoore A D
zipWith f = ap ∘ map f

cat : Moore A B → Moore B C → Moore A C
...

Regular expressions

Lang : 𝒰 → 𝒰
Lang A = Moore A Bool

∅ : Lang A
∅ = pure false

ε : Lang A
ε = mre true λ _ → ∅

char : A → Lang A
char a = Mre false λ x → 
           if ⌊ x ≟ a ⌋ then ε else ∅

compl : Lang A → Lang A
compl = map not

_⋃_ : Lang A → Lang A → Lang A
_⋃_ = zipWith _or_

_⋂_ : Lang A → Lang A → Lang A
_⋂_ = zipWith _and_

Mealy automata

data Mealy (X A : 𝒰) : 𝒰 where
  mly : (X → A × ▹ Mealy X A) → Mealy X A

data Moore (X A : 𝒰) : 𝒰 where
  mre : A → (X → ▹ Moore X A) → Moore X A

Mealy X A ≅ Stream X → Stream A

transducer automaton

Resumptions

data Res (I O A : 𝒰) : 𝒰 where
  ret  : A → Res I O A
  cont : (I → O × ▹ Res I O A) → Res I O A
  • A Mealy automaton that possibly terminates
  • a combination of a partiality and state monad

Harrison, Procter, [2015] "Cheap (But Functional) Threads”

Coroutines

Passing control back and forth via thunks is conceptually programming with coroutines

 

Can be compiled into patterns of communication between consumer and producer automata

data Consume (A B : 𝒰) : 𝒰 where
  end  : B → Consume A B
  more : (A → ▹ Consume A B) → Consume A B

pipe-body : ▹ (Stream A → Consume A B → Part B)
          →    Stream A → Consume A B → Part B
pipe-body p▹ _           (end x)   = now x
pipe-body p▹ (cons h t▹) (more f▹) = later (p▹ ⊛ t▹ ⊛ f▹ h)

pipe : Stream A → Consume A B → Part B
pipe = fix pipe-body

Part 5

Where to go next?

Extra ideas & conclusions

Clocked type theory

  • We can work "under" thunks but not remove them
  • Delayedness never decreases
  • Weaker than proper coinduction
  • Can be extended by a constant ☐ modality or clock variables to allow forcing "completed" thinks
  • force : (∀ κ → ▹ κ (A κ)) → ∀ κ → A κ
  • Controlled violation of causality
  • E.g. we can write everyother function on streams

Bird's algorithm

  • aka replaceMin
  • later generalized to value recursion (MonadFix) in Haskell
  • given a binary tree with data in leaves, replaces all values with a minimum in a single pass

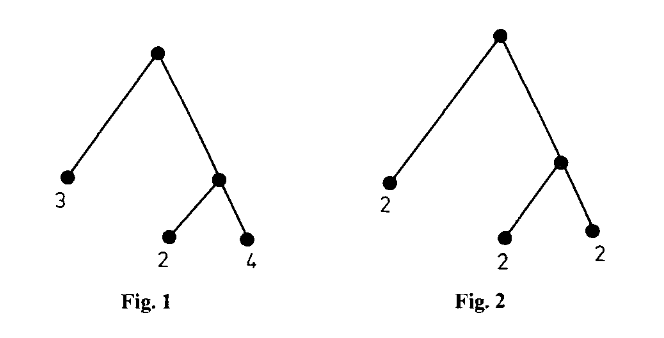
Bird's algorithm

Classical form is somewhat weird

replaceMin :: Tree -> Tree

replaceMin t = 
  let (r, m) = rmb (t, m) in r 
  where 
  rmb :: (Tree, Int) -> (Tree, Int) 
  rmb (Leaf x, y) = (Leaf y, x) 
  rmb (Node l r, y) = 
    let (l',ml) = rmb (l, y) 
        (r',mr) = rmb (r, y) 
     in 
   (Node l' r', min ml mr)

Guarded decomposition

  • We can decompose this in two temporal phases
  • Compute the minimum and construct the thunk
  • Then run the thunk
  • Uses the feedback combinator
    feedback : (▹ A → B × A) → B
    feedback f = fst (fix (f ∘ snd     ⍉_))

  • Inserts intermediate data between steps

  • Cannot run the thunk without clocks

Guarded decomposition

replaceMinBody : Tree ℕ 
               → ▹ ℕ → ▹ (Tree ℕ) × ℕ
replaceMinBody (Leaf x) n▹ = Leaf ⍉ n▹ , x
replaceMinBody (Br l r) n▹ =
  let (l▹ , nl) = replaceMinBody l n▹
      (r▹ , nr) = replaceMinBody r n▹
    in
  (Br ⍉ l▹ ⊛ r▹) , min nl nr
  
feedback : (▹ A → B × A) → B
feedback f = fst (fix (f ∘ (snd ⍉_)))

-- main function

replaceMin : Tree ℕ → ▹ Tree ℕ
replaceMin t = feedback (replaceMinBody t)

Continuations

  • We can reason about control-flow based algorithms
  • Harper's algorithm for matching on regexps with continuations
  • Hofmann's algorithm for tree BFS
data StdReg = NoMatch | MatchChar Char | Or StdReg StdReg
            | Plus StdReg | Concat StdReg StdReg
            
type MatchT = (String -> Bool) -> Bool

matchi :: StdReg -> Char -> String -> MatchT
matchi  NoMatch       c cs k = False
matchi (MatchChar c') c cs k = if c == c' then k cs else False
matchi (Or r1 r2)     c cs k = matchi r1 c cs k || matchi r2 c cs k
matchi (Plus r)       c cs k = matchi r c cs (\cs -> k cs || matchh cs (Plus r) k)
matchi (Concat r1 r2) c cs k = matchi r1 c cs (\cs -> matchh cs r2 k)

matchh :: String -> StdReg -> MatchT
matchh []       r k = False
matchh (c : cs) r k = matchi r c cs k

match :: String -> StdReg -> Bool
match s r = matchh s r null

Breadth-first traversal

  • Another form of a binary tree, data on both leaves and nodes
  • Compute a breadth-first traversal

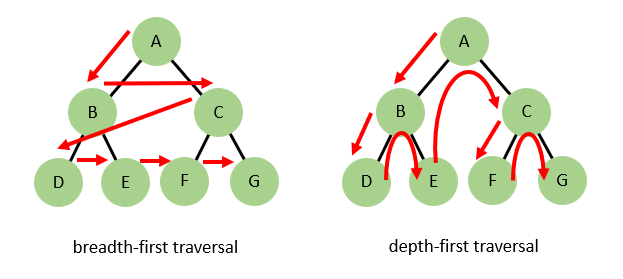
Hoffman's algorithm

  • Typically done with queues
  • Hoffman invented a purely functional continuation-based algorithm in 1993
  • Requires a intermediate (non-strictly) positive datatype
data Rou A where
  Over : Rou A
  Next : ((Rou A → List A) → List A) → Rou A
---        ^^^^^

Hoffman's algorithm

  • We can encode this in guarded theory by switching to Colists
  • requires smart constructors that transport terms over the fixpoint (un)rolling equalities internally
data RouF (A : 𝒰) (R▹ : ▹ 𝒰) : 𝒰 where
  overRF : RouF A R▹
  nextRF : ((▸ R▹ → ▹ Colist A) → Colist A) → RouF A R▹

Rou : 𝒰 → 𝒰
Rou A = fix (RouF A)

overR : Rou A
nextR : ((▹ Rou A → ▹ Colist A) → Colist A) → Rou A

Stream calculus

exact real numbers, series

stream differential equations

Search algorithms

  • can encode sequential topology
  • constructive Tychonoff's theorem
→c-searchable : (ds : is-discrete X) 
              → c-searchable X (discrete-clofun ds)
              → c-searchable (Stream X) (closenessˢ ds)

A generic framework for

search/selection/minimization algorithms

Vs coinduction

  • Coinductive mechanisms are more liberal
  • Productivity checker is purely syntactic
  • Spend a few hours on a proof, get shot down
  • Guarded constructions are type-directed

Conclusion

  • A principled way to work with non-termination
  • A common theme is overcoming syntactic approximations
  • Thunks, streams, partiality
  • Non-strictly positive datatypes
  • Synthetic topology and domain theory
  • Concurrency models (quotienting & cubical gizmos)

Working repos

Literature

Contacts