Les économies d(e quelles) agglomérations?
Explorations méthodologiques à partir de lois d'échelle économiques urbaines
Olivier Finance, Université catholique de Louvain, Université Paris 1
Séminaire des directeurs régionaux de l'INSEE
Montrouge - Lundi 26 Mars 2018

Clémentine Cottineau, CNRS, University College London





Économies d'agglomération
> Investissements étrangers
> Inégalités
> New Economic Geography
> Scaling et systèmes complexes
Une raison de l'intérêt d'autres disciplines
envers le territoire
Autres quantités éco varient avec taille de population
Problème de définition (ville et ensemble de référence)
La question des phénomènes non ubiquitaires
La délimitation des villes
L'exemple des investissements étrangers en France
L'exemple des inégalités salariales en France
Finance O., Cottineau C., 2018, Are the absent always wrong? Dealing with zero-values in urban scaling
Cottineau C., Finance O., Hatna E., Arcaute E., Batty M., 2018
Enjeux de spatialisation
et de définition
Defining urban clusters to detect agglomeration economies
Évaluation de la variation d'une quantité économique Q avec la taille de la population P
Application à des territoires urbains i
Interprétation de comme indicateur de non-linéarité
> Problème de seuil et significativité
> Interprétation théorique
Méthodologie commune :
scaling ou lois d'échelle
> 1 : super-linéarité
Interprétation statique vs. dynamique
Conséquences en termes
de recommandations publiques
~ 1 : linéarité
< 1 : sub - linéarité
Méthodologie commune :
scaling ou lois d'échelle
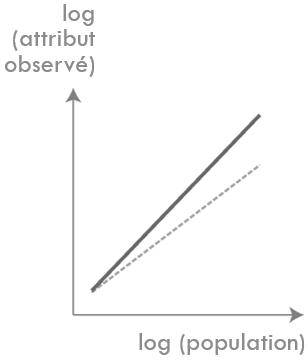
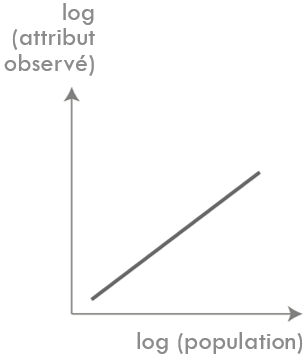
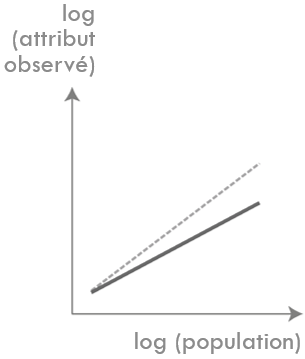
Superlinéarité
Linéarité
Sublinéarité
Unité de l'ensemble
Définition des éléments
Moyenne des observations
Scaling : biologie vs. études urbaines

Kleiber, 1932

West, 2017
West, Bettencourt, 2013

> implicite
Ensemble des données utilisées
Taille
de la ville
Définition
de la ville
Variables
d'étude
Finance O., Cottineau C., 2018
Cottineau C., et al., 2018
Population
(recensement)
Ménages
(recensement)
...
Zonage
en Aires Urbaines
(INSEE)
Densité de population
(CORINE Land Cover)
Migrations
domicile-travail
(INSEE)
Emplois
(INSEE)
Revenus
(IRCOM)
Salaires
(base CLAP)
Stock d'IDE
(ORBIS, LIFI et CLAP)
Flux d'IDE
(Financial Times)
Finance O., Cottineau C., 2018
Cottineau C., et al., 2018
Premier cas :
Les investissements des firmes transnationales étrangères
Stratégies de localisation
des firmes transnationales étrangères
Inégalités d'intégration à l'échelle mondiale
> Processus de mise en relation
> Acteurs majeurs : firmes transnationales
> Intégration / exclusion : principalement Nord-Nord
Et à échelle plus fine ?
> Dépasser échelle inter-nationale et "villes mondiales"
> Polarisation de l'activité économique par les villes =
échelon d'analyse retenu
> Système de villes français =
confrontation à la hiérarchie urbaine
Stratégies de localisation
des firmes transnationales étrangères
Démarche générale :
confrontation des IDE à la hiérarchie urbaine

Décomposition
des IDE
Confrontation à la hiérarchie urbaine
Stratégies de localisation
des firmes transnationales étrangères
Exemple :
ArcellorMittal

Stratégies de localisation
des firmes transnationales étrangères
Une approche "dynamique" :
concentration / diffusion dans le temps ?
> Stocks d'IDE localisés
= ensemble des emplois dans les établissements
contrôlés depuis l'étranger en 2008
versus
> Flux d'IDE localisés
= ensemble des emplois dans les sites
nouvellement créés par les firmes étrangères
entre 2003 et 2015
versus
> Emplois
Investissements étrangers :
Paris... et puis ?

Stock d'IDE :
Emplois dans
établissements
contrôlés depuis
l'étranger
(2008)

Investissements étrangers :
Paris... et puis ?

Flux d'IDE :
Emplois dans
sites nouvellement créés par les firmes étrangères
(2003-2015)

Investissements étrangers :
Paris... et puis ?

Benchmark :
Emplois dans
l'ensemble des établissements
(au sein d'une
firme ou non)

Investissements étrangers :
Paris... et puis ?






Investissements étrangers :
Paris... et puis ?


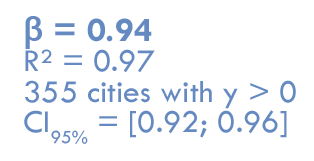

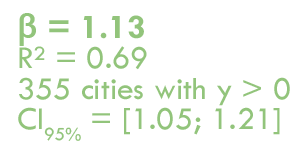

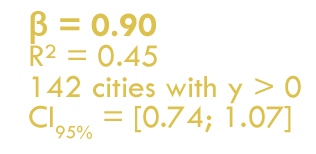
Les lois d'échelle classiques,
inappropriées ?
Une diffusion hiérarchique des investissements, à rebours de la littérature ?
Pourtant, faisceau d'indices en contradiction avec les résultats précédents
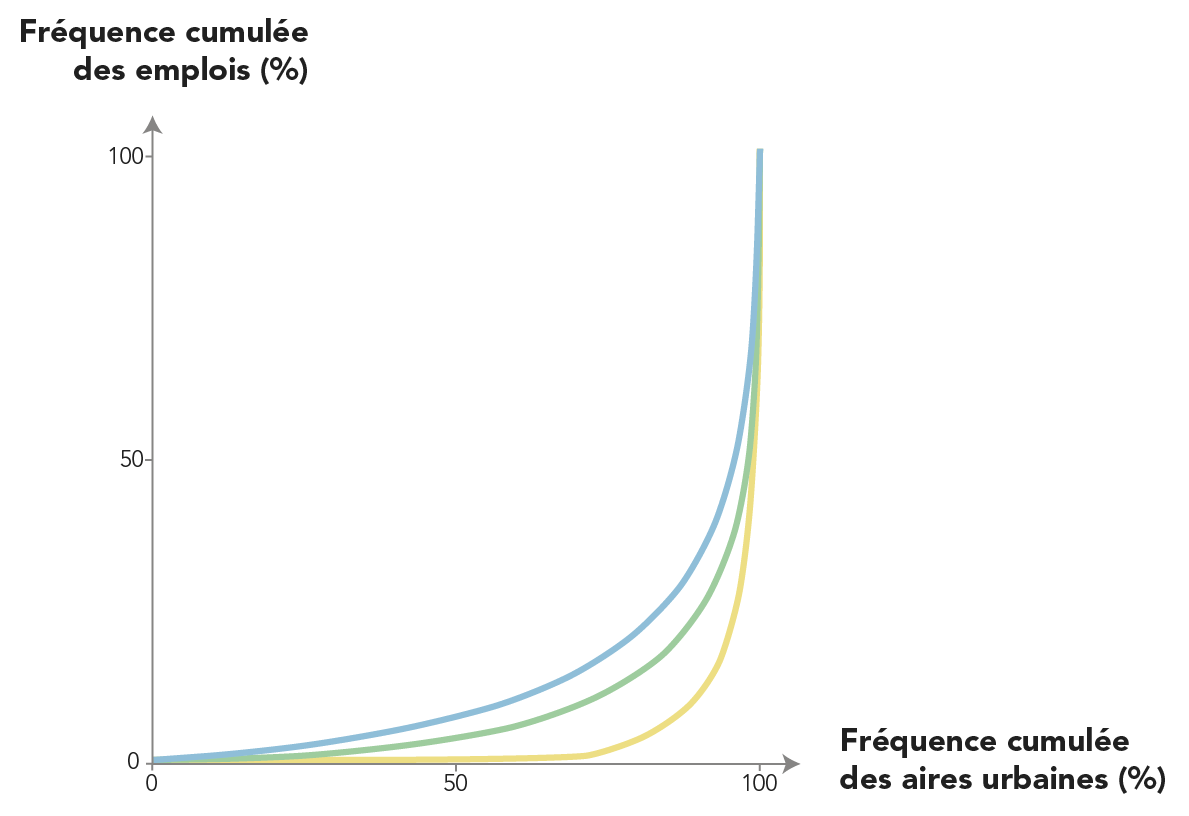



Gini = 0.746
Gini = 0.828
Gini = 0.938
Les lois d'échelle classiques,
inappropriées ?
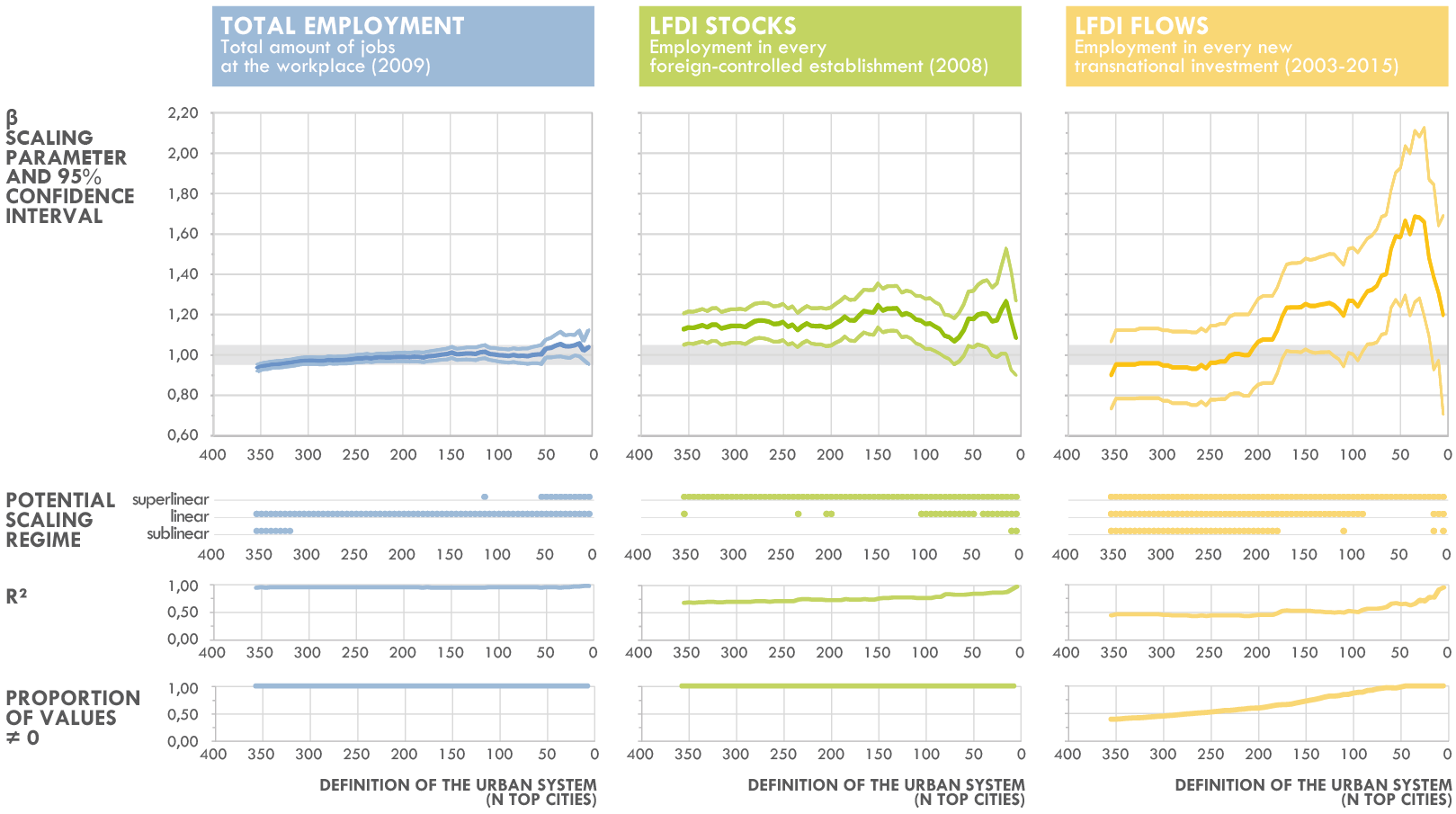
Les lois d'échelle classiques,
inappropriées ?

Les lois d'échelle classiques,
inappropriées ?

Les lois d'échelle classiques,
inappropriées ?
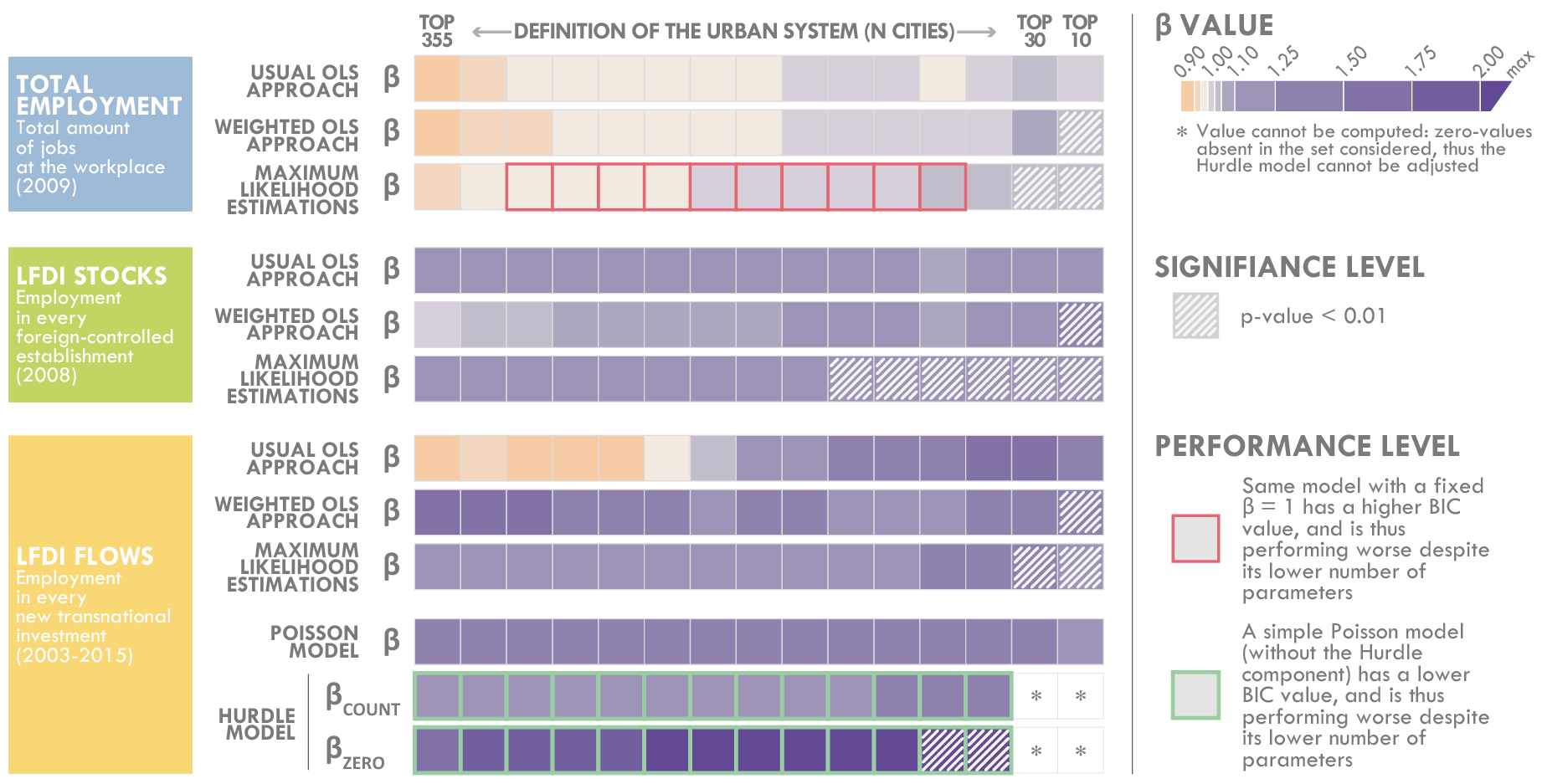
Les lois d'échelle classiques,
inappropriées ?
A (...) limitation of the usual approach is that it requires removing the datapoints with yi = 0 (because it requires computing ln yi).
This filtering is arbitrary because y = 0 is usually a valid observation (e.g. cities without any patents filed).

[Leitão et al., 2016]
Approche classique :
Ajustement par la méthode des moindres carrés
Qualité de l'ajustement estimée par R²
Validation via l'intervalle de confiance à 95%
Les lois d'échelle classiques,
inappropriées ?
Des méthodes additionnelles :
&
Lois d'échelle pondérées
Données brutes "lissées" par classes de taille
Suppression artificielle des valeurs nulles
Les lois d'échelle classiques,
inappropriées ?
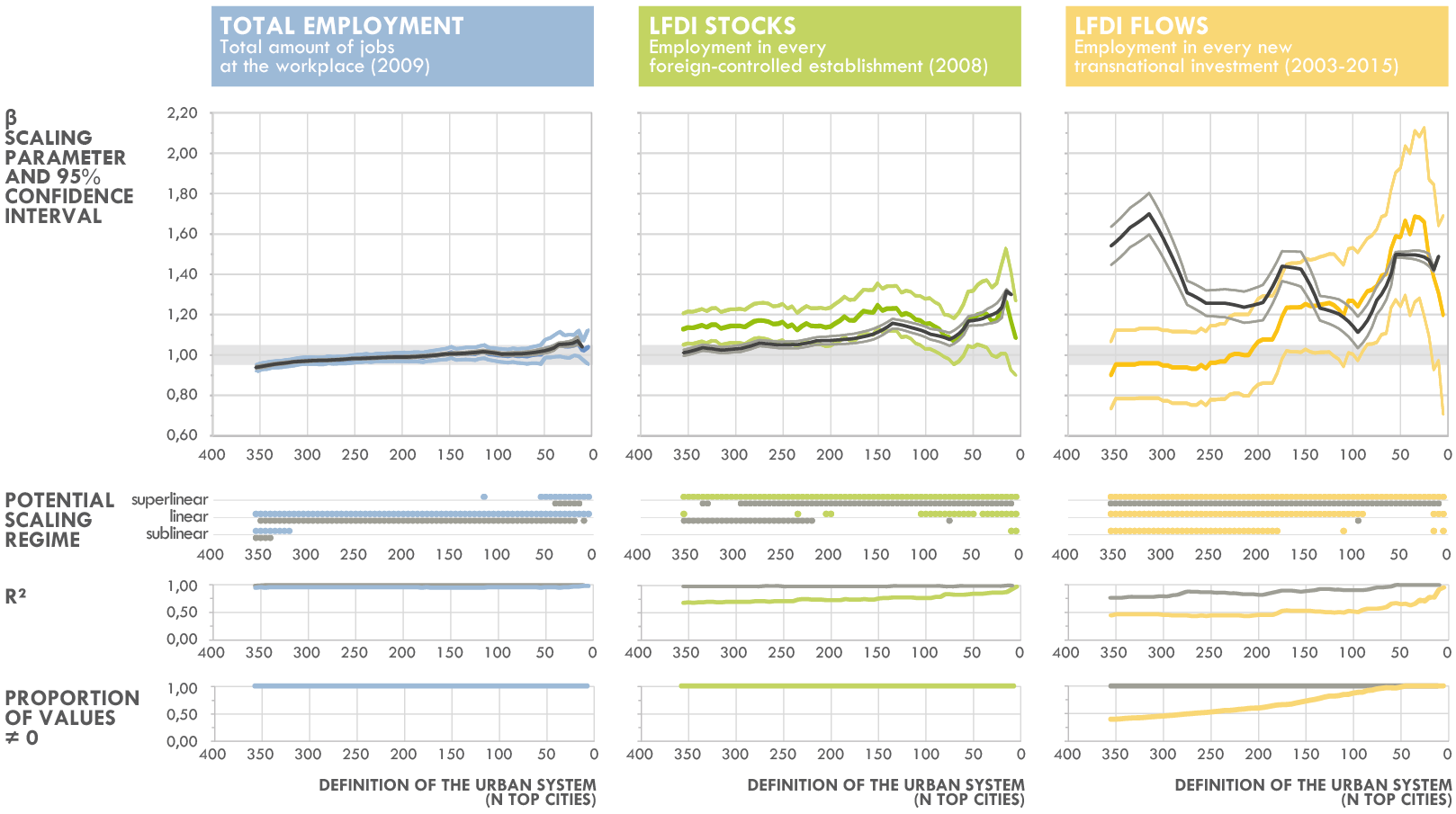
Les lois d'échelle classiques,
inappropriées ?

Les lois d'échelle classiques,
inappropriées ?
= inversion des interprétations
Des méthodes additionnelles :
&
Lois d'échelle pondérées
Données brutes "lissées" par classes de taille
Suppression artificielle des valeurs nulles
Les lois d'échelle classiques,
inappropriées ?
Maximum Likelihood estimation
&
Comparaison d'un modèle contraint avec β = 1 et d'un modèle avec β libre, en termes d'ajustement et de parsimonie
= inversion des interprétations
Des méthodes additionnelles :
&
Lois d'échelle pondérées
Données brutes "lissées" par classes de taille
Suppression artificielle des valeurs nulles
Les lois d'échelle classiques,
inappropriées ?

Les lois d'échelle classiques,
inappropriées ?
= résultats en faveur des interprétations des lois d'échelle pondérées
Maximum Likelihood estimation
&
Comparaison d'un modèle contraint avec β = 1 et d'un modèle avec β libre, en termes d'ajustement et de parsimonie
= inversion des interprétations
Des méthodes additionnelles :
&
Lois d'échelle pondérées
Données brutes "lissées" par classes de taille
Suppression artificielle des valeurs nulles
Les lois d'échelle classiques,
inappropriées ?
Modèle Hurdle et comparaison à modèle Poisson
&
Considération spécifique des valeurs nulles, estimation d'un β relatif aux valeurs nulles et d'un β relatif aux valeurs positives
= résultats en faveur des interprétations des lois d'échelle pondérées
Maximum Likelihood estimation
&
Comparaison d'un modèle contraint avec β = 1 et d'un modèle avec β libre, en termes d'ajustement et de parsimonie
= inversion des interprétations
Des méthodes additionnelles :
&
Lois d'échelle pondérées
Données brutes "lissées" par classes de taille
Suppression artificielle des valeurs nulles
Les lois d'échelle classiques,
inappropriées ?

Les lois d'échelle classiques,
inappropriées ?
Modèle Hurdle et comparaison à modèle Poisson
&
Considération spécifique des valeurs nulles, estimation d'un β relatif aux valeurs nulles et d'un β relatif aux valeurs positives
= résultats en faveur des interprétations des lois d'échelle pondérées
Maximum Likelihood estimation
&
Comparaison d'un modèle contraint avec β = 1 et d'un modèle avec β libre, en termes d'ajustement et de parsimonie
= inversion des interprétations
Des méthodes additionnelles :
&
Lois d'échelle pondérées
Données brutes "lissées" par classes de taille
Suppression artificielle des valeurs nulles
= renforcement de la concentration dans les grandes villes
Les lois d'échelle classiques,
à compléter par d'autres modèles
Lois d'échelle classiques : artefacts de modélisation dans le cas de grandeurs non-ubiquistes
> Révéleraient une diffusion de l'investissement
étranger pourtant erronée
À compléter par des modèles prenant en compte explicitement les valeurs nulles
> Poursuite de la concentration des investissements
étrangers vers le haut de la hiérarchie urbaine
Autres effets à considérer ?
Deuxième cas :
Salaires et revenus dans les villes françaises
Les économies d'agglomération
Mécanismes de concentration dans l'espace
> Sharing (infrastructure à plusieurs échelles)
> Matching (marché de l'emploi - régional)
> Learning (lieu de travail - local)
Empiriquement, du zipcode à la région
> si les différents groupes économiques sont associés à différents types d'espace de résidence et de travail
Et les inégalités?
Marshall, 1920
Duranton, Puga, 2004
Rosenthal, Strange, 2001
Ciccone, 2002
Définition des quantités économiques
Salaires totaux
> CLAP, 2008
Revenus totaux
> IRCOM, 2012
Indice de Gini
> Par décile de salaires / groupes de revenu
Indice de ségrégation
> Ordinal Variation Ratio Index
Füller, 1979
Reardon, 2009
Les économies d'agglomération,
quelle(s) définition(s) de la ville ?

Les économies d'agglomération,
quelle(s) définition(s) de la ville ?

Quelle(s) définition(s) de la ville ?
Variation de densité D Variation de navetteurs F
Variation de population P
> Agrégration pour chaque combinaison.
Credits: Y. Jiang, T. Russell, C. Cottineau, E. Arcaute
Quelle(s) définition(s) de la ville ?

39 valeurs de D
x 21 valeurs de F
x 6 valeurs de P
= 4929 représentations du système de villes
Les économies d'agglomération,
quelle(s) définition(s) de la ville ?

39 valeurs de D
x 21 valeurs de F
x 6 valeurs de P
= 4929 représentations du système de villes
x N variables
x M populations
> 1M de régressions
Lecture des résultats


Lecture des résultats

Économies d'agglomération et inégalités

Économies d'agglomération et inégalités
> La mesure des économies d'agglomération dépend de l'échelle d'observation, en lien avec les mécanismes générateurs
> Les grandes villes apparaissent au moins aussi riches que les plus petites, jamais moins en moyenne
> Les grandes villes apparaissent au moins aussi inégales que les plus petites, jamais moins en moyenne
Conclusion partielle
Conclusion générale
Conclusion


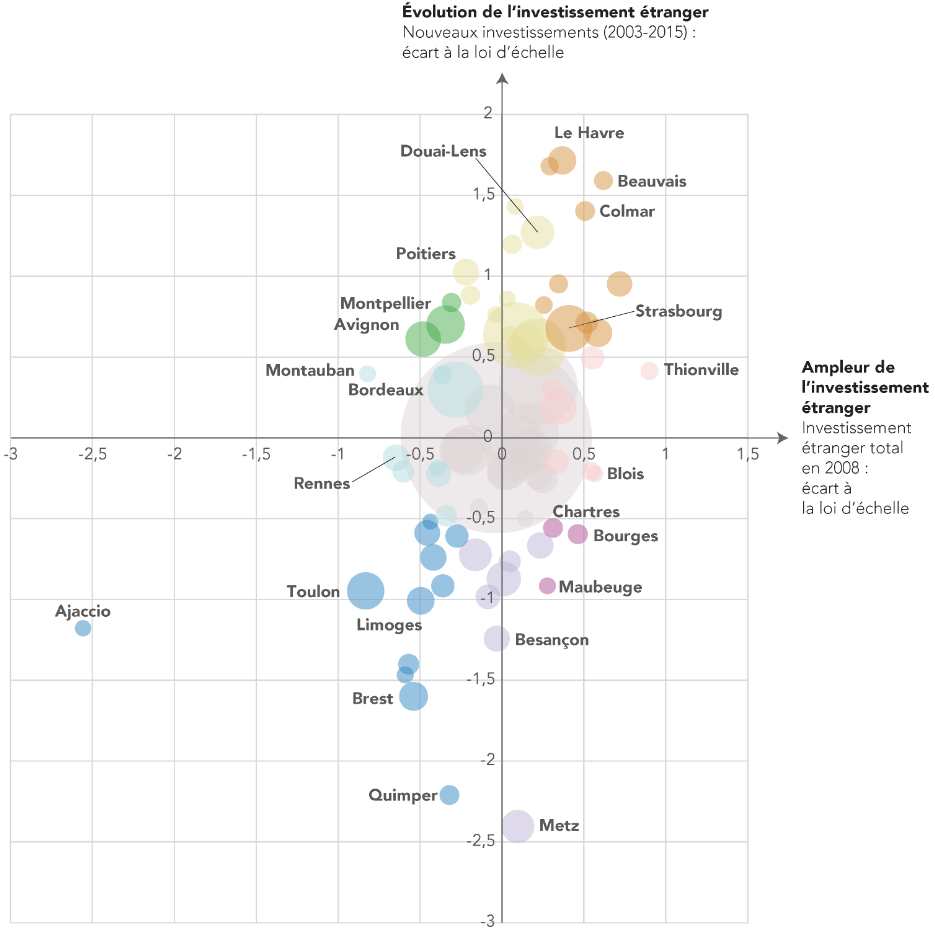
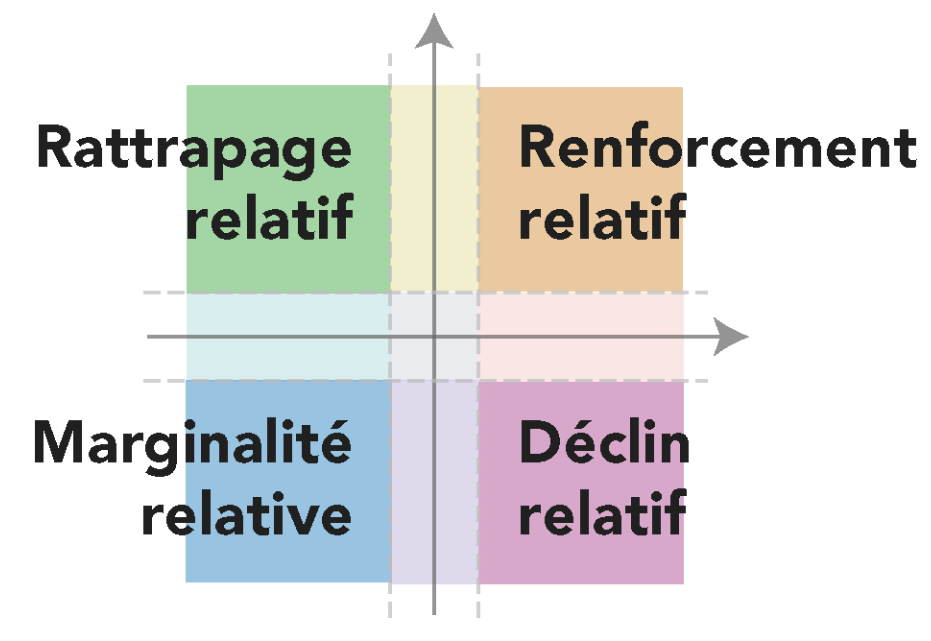


&
Conclusion
Lier les régimes d'explication des inégalités entre échelles géographiques, du quartier à la nation
> Par la mesure
> Par des modèles
Conclusion

Les économies d(e quelles) agglomérations?
Explorations méthodologiques à partir de lois d'échelle économiques urbaines
Olivier Finance, olivier.finance@uclouvain.be
Séminaire des directeurs régionaux de l'INSEE
Montrouge - Lundi 26 Mars 2018

Clémentine Cottineau, c.cottineau@ucl.ac.uk




