
How do you know when someone dies?
Not to be confused with lifelines:
(survival analysis in Python)
What is Customer Lifetime Value?
According to Google and every business article ever:








It's the sum of all the earnings you expect to receive from a customer over their lifetime with you.
Why is CLV Important to a company?
- How much money can I spend per acquisition?
- Do customers from Twitter or Facebook give me more CLV?
- What is the net-worth of my company? Should customers be treated as assets on my balance sheet?
Classify Business Settings
1. According to numbers presented in a news release that reported Vodafone Group Plc's results for the six months ended September 2012, Vodafone UK as 10.8 million "pay monthly" customers
2. In his "Q3 2012 Earnings Conference Call", the CFO of Amazon commented that "active customer accounts exceeded 188 million", where customers are considered active when they have placed an order during the preceding twelve-month period.
Which of the following is inaccurate?
Contractual vs Noncontractual settings
Contractual: we observe when the customers dies.
Non-contractual: the time at which a customer dies is unobserved.
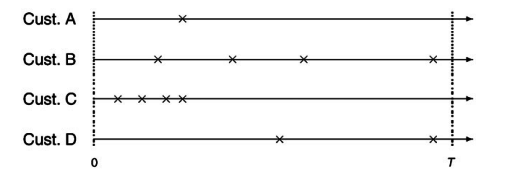
When do we know a customer is still alive?
Let's create a model of customers
1. Let's assume customers will continuing buying from us until they "die".
2. Their death rate is constant (but different constants across individuals).
3. Assume exponential time between purchases (with different rates across individuals)
Call this the Pareto model
- An individual purchases Poisson-ly, with rate λ, over their lifetime.
- λ comes from a Gamma(r, α)
- A customer's lifetime is exponentially distributed, with rate μ.
- μ comes from a Gamma(s, β)
Pareto/NBD model
Graphically:

1.
2.
3.
4.
But we don't know the population parameters!
Solution: use existing data/observations to infer these parameters. Nice part - we only need a few variables to do this.
Age: how old is the customer?
Frequency: how many purchases did they make?
Recency: how old was the customer at their last purchase?
Inference
1. Set up the likelihood
2. find the maximum using numerical methods
3. push the maximum point back into the distributions
Lifetimes implements this part.
penalizer_coef = 0.01
bgf = ParetoNBDFitter(penalizer_coef=penalizer_coef)
bgf.fit(rfm_customers['frequency'], rfm_customers['recency'], rfm_customers['t'])
print bgf
# <lifetimes.ParetoNBDFitter: fitted with 40063 subjects, a: 0.34, alpha: 945.35, b: 0.39, r: 0.19>
print model.conditional_probability_alive(frequency=0,recency=0,T=109)
# 0.46701904847776876
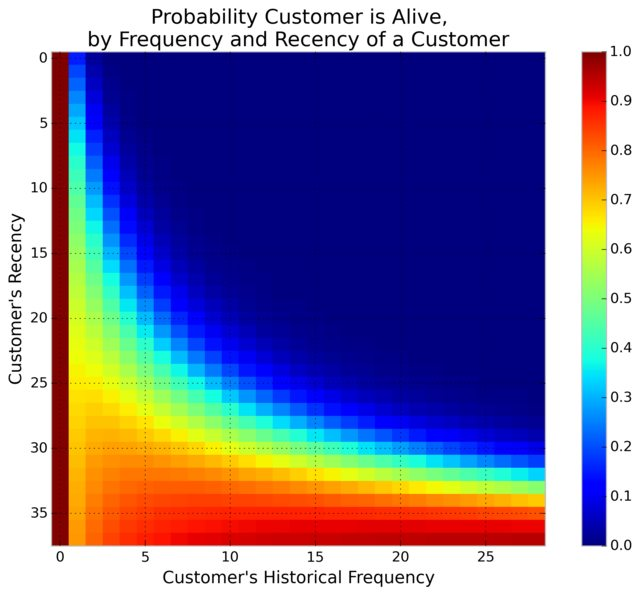
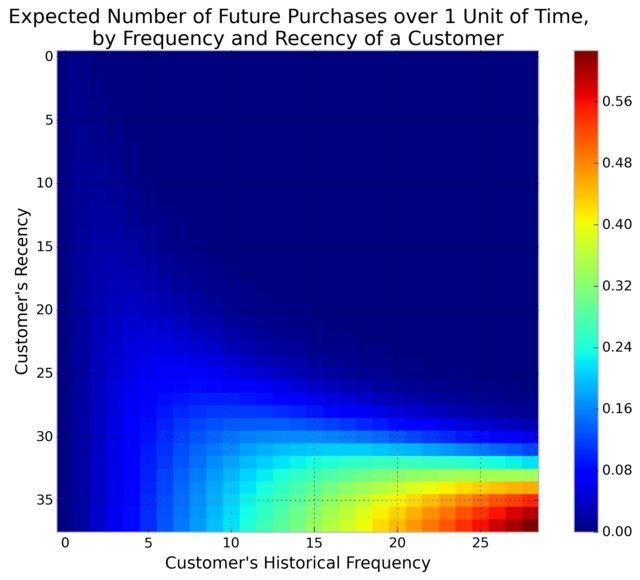
Let's create another model of customers.
1. Let's assume customers will continuing buying from us until they "die".
2. After each additional purchase they have a p-percent chance of dieing (p is unique to the individual).
3. Assume exponential time between purchases.
Call this the BG/NDB model
Shopify
Applications
- Not purchases, but storefront sessions can be used: a visitor often comes to your site, but hasn't in months - they've probably died.
- Partners: partners never tell us they are leaving, they just stop sending us new shops.
- App usage: when does a merchant churn from an app without explicitly uninstalling it?
Other interesting applications
- Visits to a hospital. We track check-ins, but don't see them "die".
- "Health" of church goers. Did a family lose their faith?
- Any setting where we have have transactions (visits, purchases, check-ins), and underlying death is unobserved.
Questions?
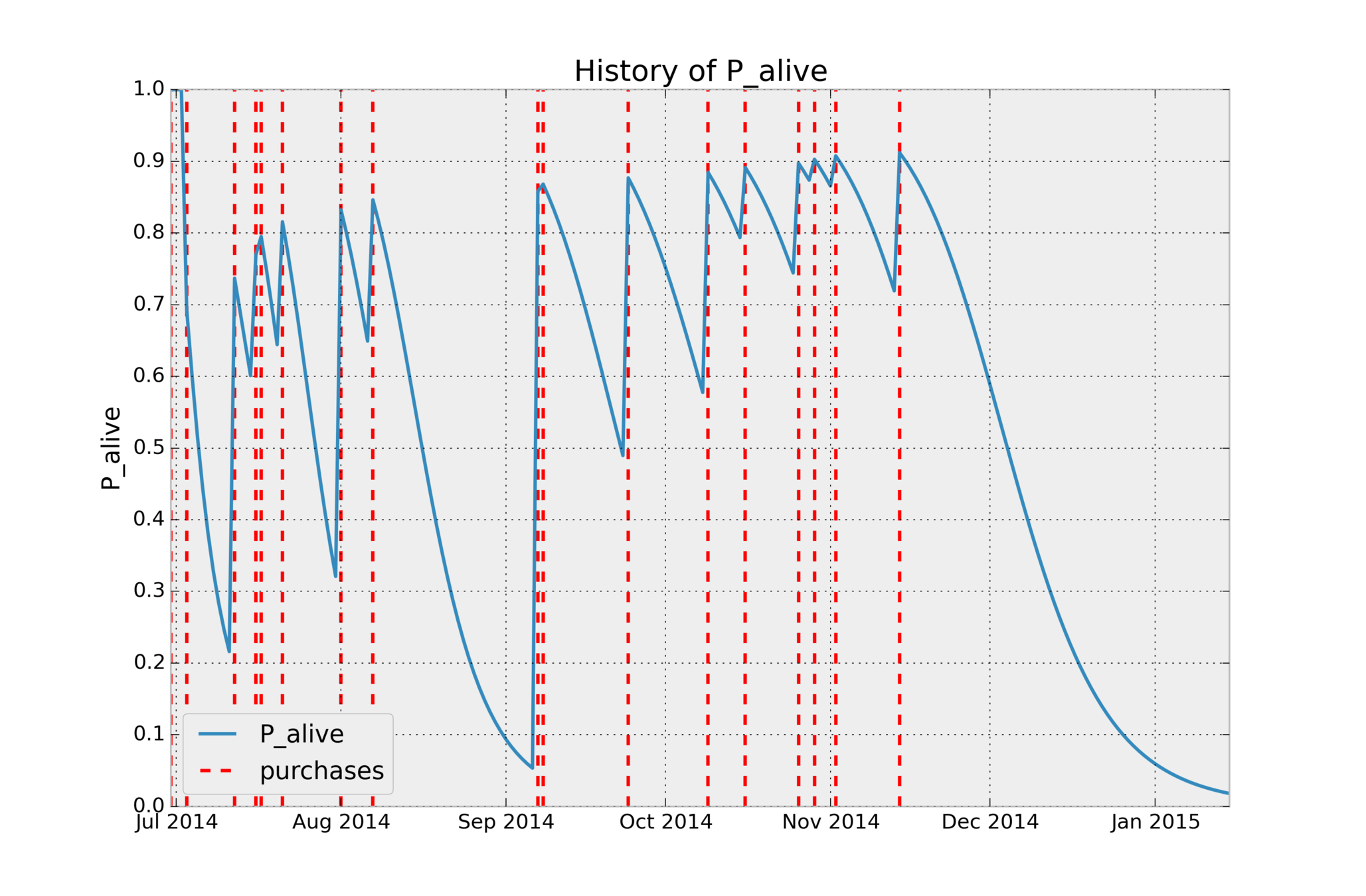
How does this work for seasonal sales?
Pretty good! Seasonal sales like Christmas are only a blip on the cumulative total number of orders. This might "reawaken" dead customers though, which is not part of our model.
What about Bayesian inference instead of MLE?
Absolutely - this is almost desirable when you are dealing with small businesses who lack lots of data - you want to see the uncertainty in your estimates.
Dan W. at Pass the ROC does a great job of this:
http://danielweitzenfeld.github.io/passtheroc/
Ex: instead of point estimates of λ, I want a distribution of what λ might be.