How does the cosmic web impact galaxy formation?

Corentin Cadiou — PhD student

In collaboration with Yohan Dubois, Christophe Pichon, Marcello Musso

MPA — 18/12/2018

An insight from theory and numerical simulations.

(Quick) Introduction

A very biased view on galaxy formation

The isotropic view

Silk&Mamon 12

Press&Schechter 74

"Mass function from first principle"

Works nicely to describe anisotropic features in the Universe

p(\mathrm{galaxy}) = f(z, \vec{r}, \dots)
p(\mathrm{galaxy}) = f(z,\dots)

Marginalise             position        

The anisotropic view

p(\mathrm{galaxy}) = f(z, \vec{r}, \dots)

Galaxies do not form anywhere at anytime

Need to create anisotropic methods → beyond two-point correlation function

Structure in the GAMA survey, Kraljic+18

How to measure position?

What metric modulates galaxy properties?

Predicting anisotropic halo properties

Excursion Set Theory

Galaxy properties & evolution from initial conditions
⇒ Find largest mass that will collapse by z at given location

Theory Real space
R M
z
\delta

Spherical collapse model:

Structure of size R will collapse at z iff

\left\{\begin{matrix}\delta(R) =& \frac{\delta_c}{D(z)} \\ M(R)=&\frac{4\pi}{3}\bar\rho R^3 \end{matrix} \right.
\delta_c = 1.68 \text{, } D(z) \text{ is the linear growth factor}

R

Compressing the spatial information

q_{ij} \equiv \nabla_i \nabla_j \varphi
\delta_{\mathcal{S}}

Height: determined by (over-)density

Curvature: controlled by (traceless) tidal tensor

\bar{q}_{ij} \equiv q_{ij} - \delta_{ij}\frac{\mathrm{Tr}(q_{ij})}{3}

Poisson equation

\mathrm{Tr}(q_{ij}) \propto \delta_\mathcal{S}

Critical point constrain*

\nabla_i\varphi=0

Results

Direction of void

Direction of filament

In filaments, halos are...

  1. more massive
  2. form later (at fixed mass)
  3. accrete more (at fixed mass)

... than in voids

(Musso, Cadiou et al 2018)

Excursion set theory + saddle point constrain

Results

The results hold for galaxies (at least simulated ones)!

Some open questions / improvements

  • Develop more subtle quantities
    • concentration, spin quantities, etc...
    • two-filament configuration (bridge effect)
    • merger rate (extending Hanami 01)
    • beyond spherical collapse? Ask Marcello Musso!
  • Take into account tidal effects…
    • by improving ES with moving barrier (e.g. Castorina+16)
    • using peak patch theory
  • Effective models of galaxy formation? (Kraljic+18)

Galaxies seem to be influenced by the cosmic web too...

This is largely WIP

Can we explain this?

We can try using numerical simulations

Simulation Setup

  • suite of zoom-in simulations (~3-5), RAMSES (Teyssier 2002)
  • Δx = 35pc, Mstar = 1.1 10⁴ M☉ Mhalo=10¹² M☉
  • Turbulent star formation (Kimm+17, Trebitsch+17)
  • Mechanical feedback (Kimm+15)
  • AGN formation with spin-regulated efficiency (Dubois+12,+14)
  • 30,000,000 tracer particles (~10/cell, 0.5/star, Cadiou+18)

*See Cadiou+18

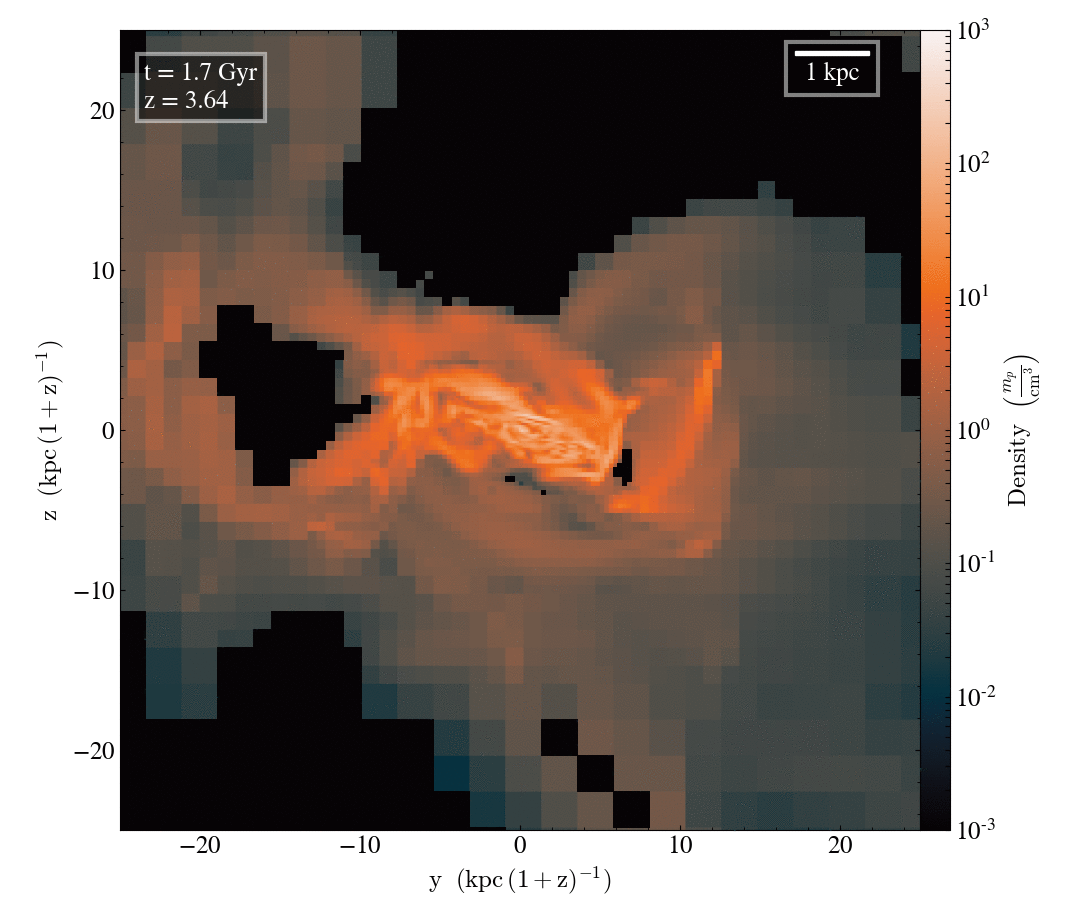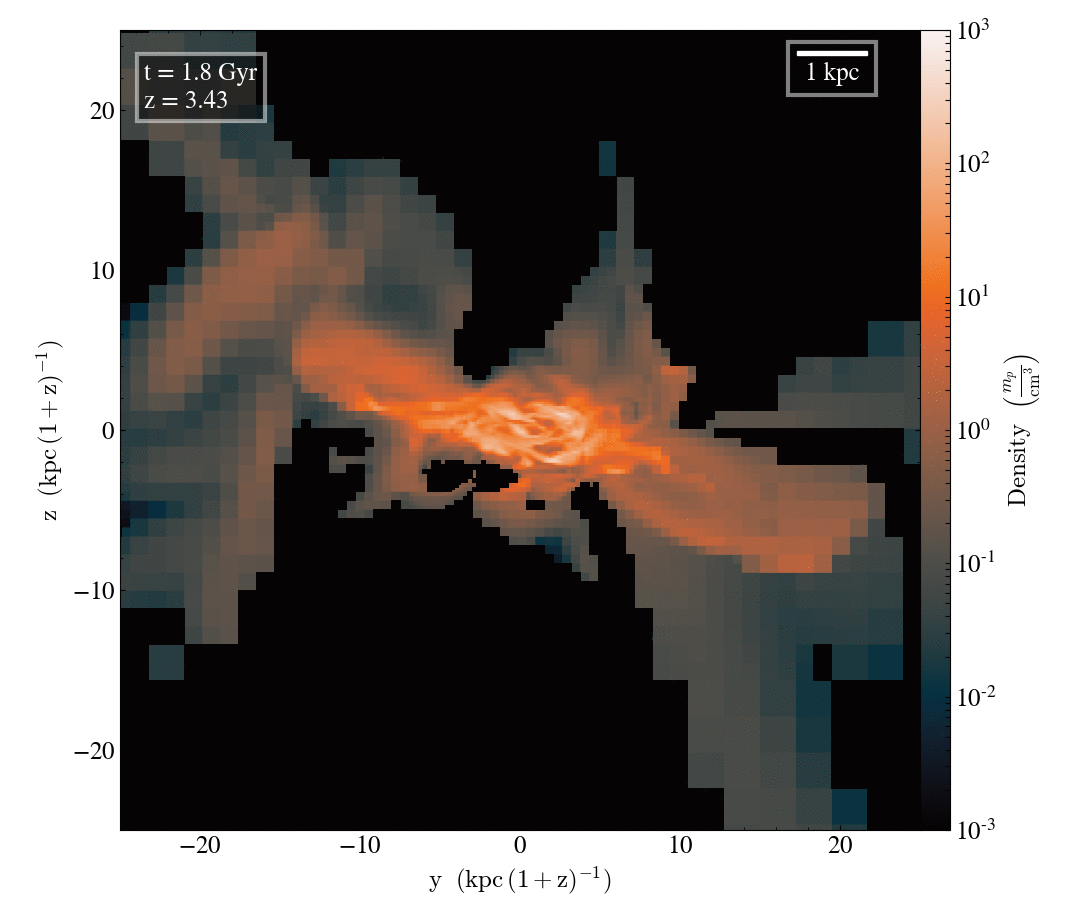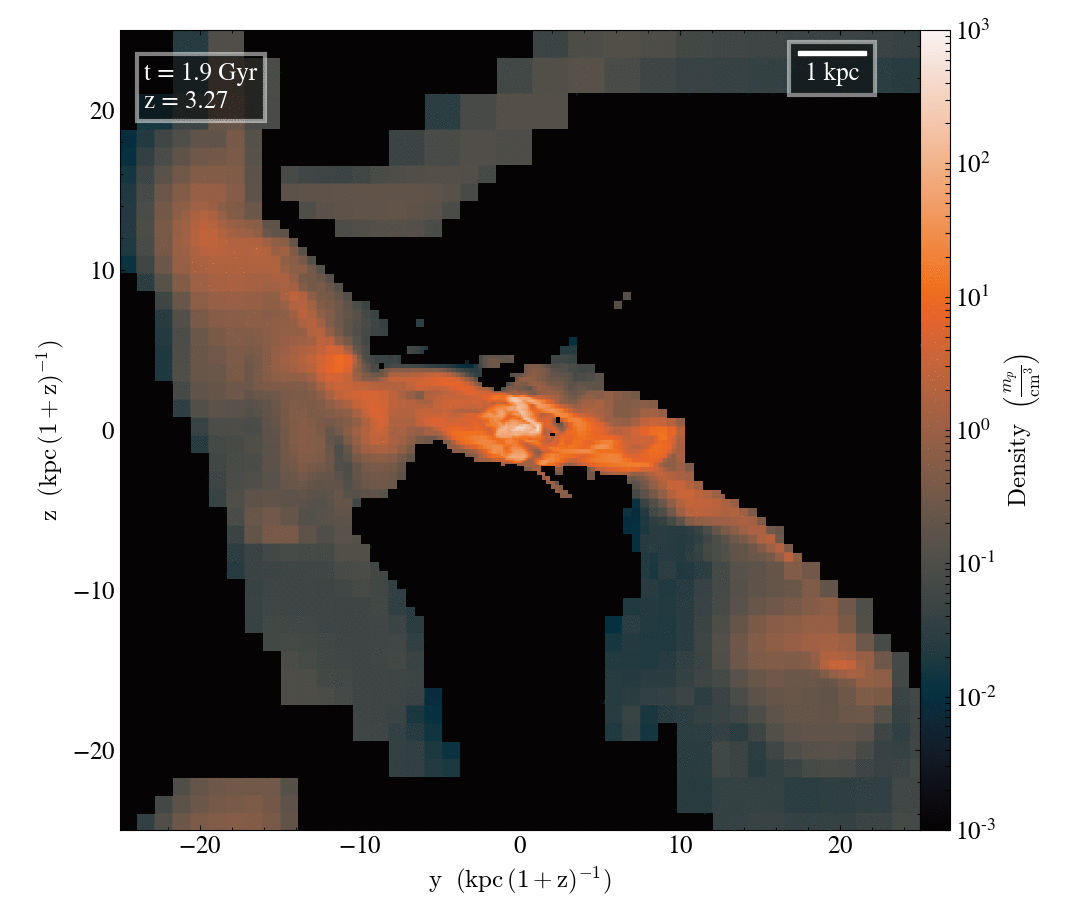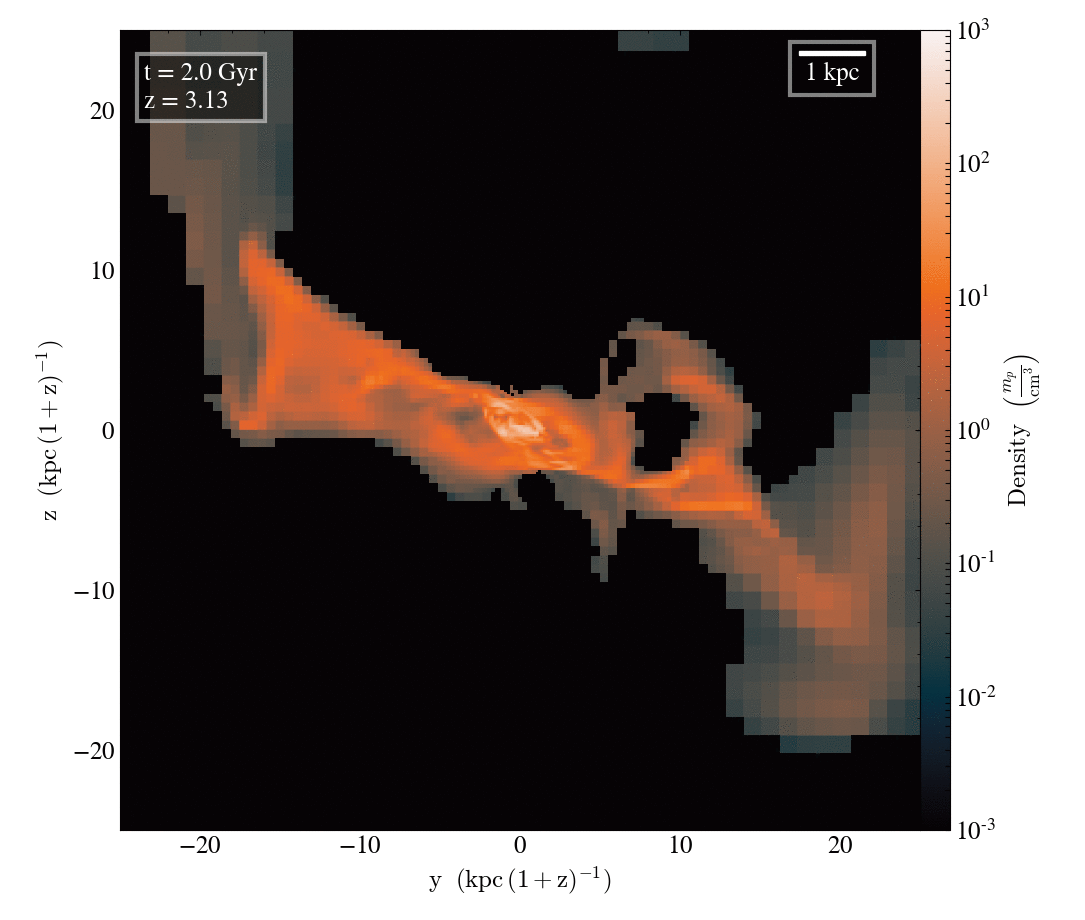
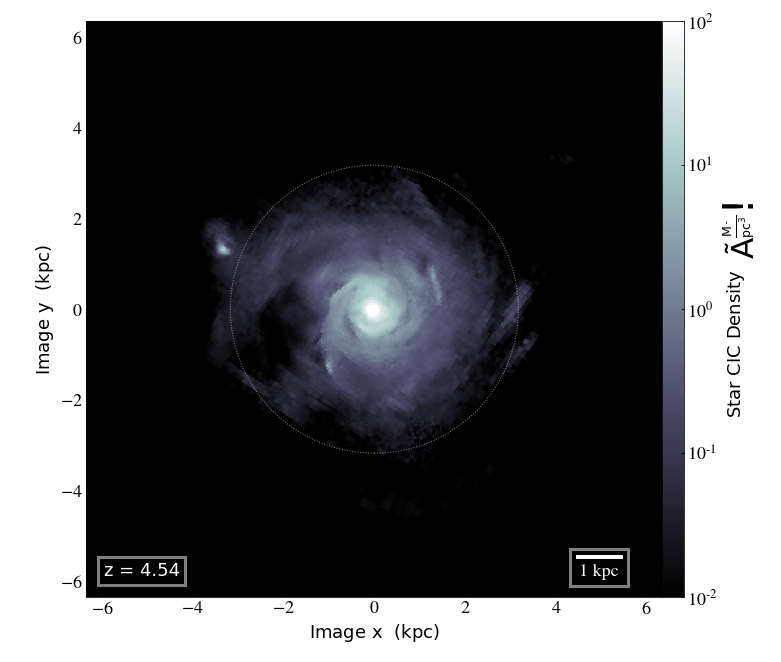
Gas density

Tracer density

Linking assembly variables to

galaxy formation?

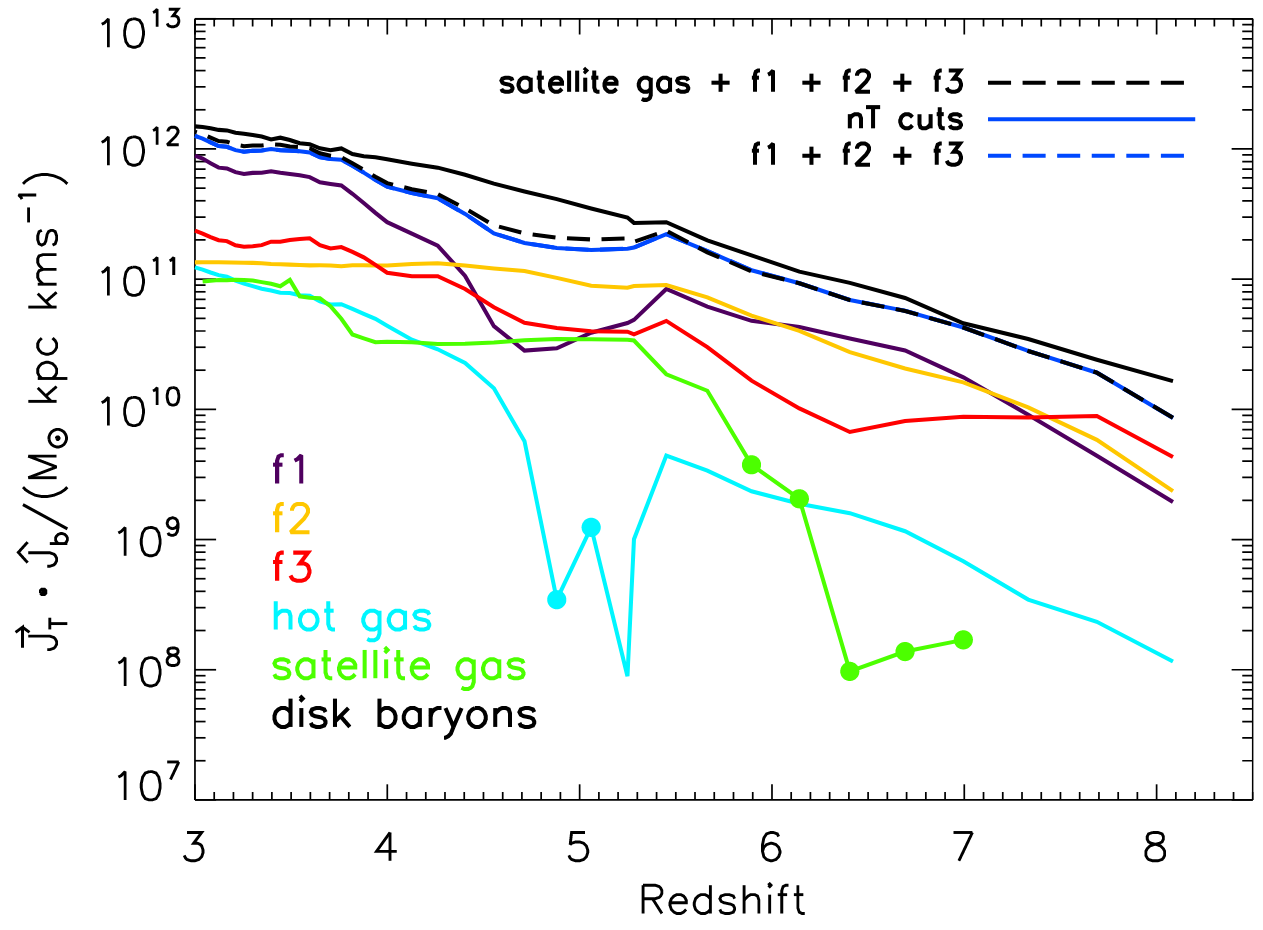
Filamentary accretion is responsible for most of the mass and angular momentum acquisition (at z>3 ; Kereš+05, Pichon+11, Tillson+12, …)

Filamentary accretion: natural "bridge" between large scale structures (cosmic web) and galaxy formation

Tillson+2015

Cadiou+ in prep

Linking assembly variables to

galaxy formation?

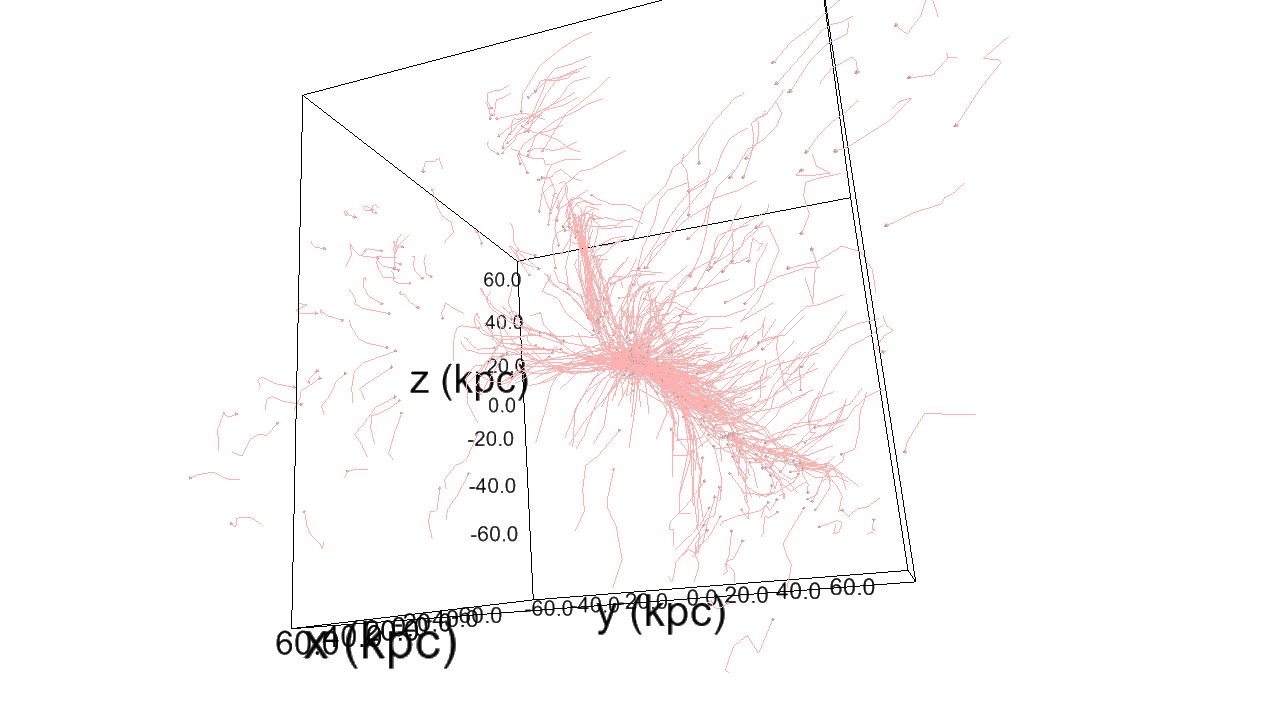
The structure of filamentary accretion

The cold flows are

  • coherent
  • resilient
  • source at large scales
  • end up at small scales
  • sAM rich

for small enough galaxies/high z

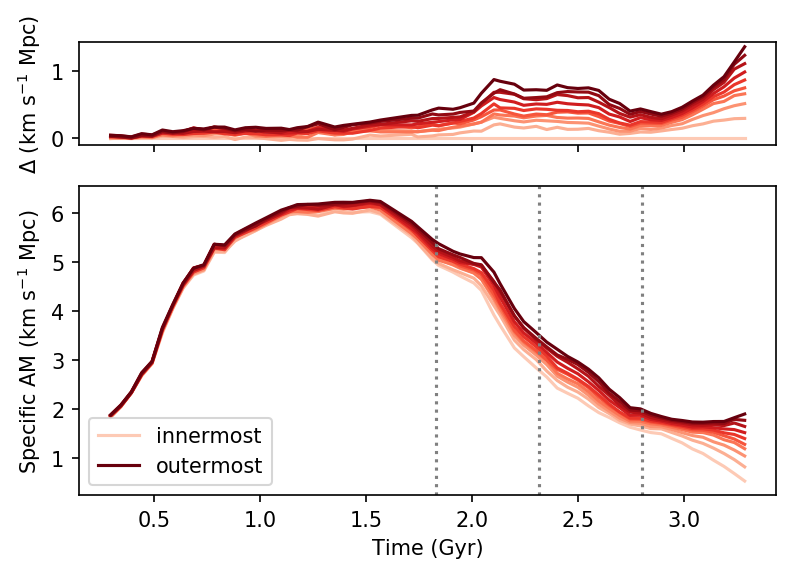
Time →

High sAM →

Innermost regions

Outermost regions

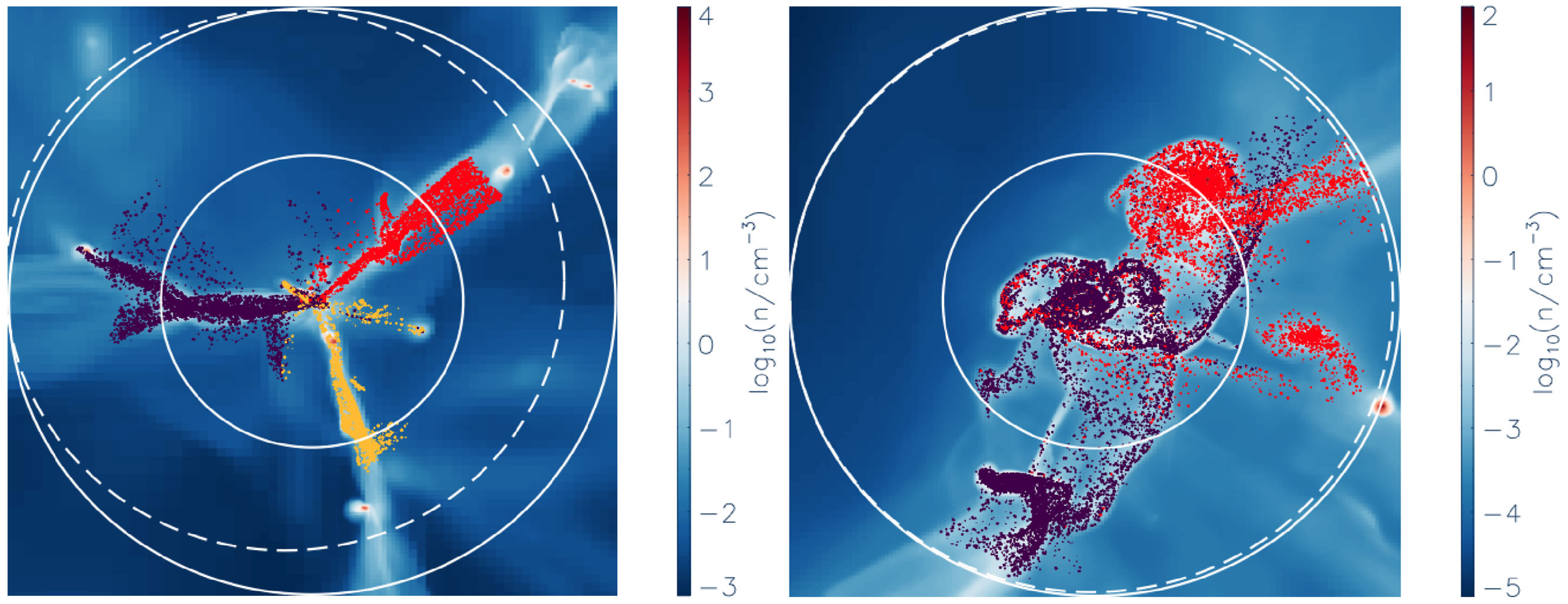
Cadiou+ in prep

Perfect candidates to transport anisotropic information from cosmic web to smale scales.

Tillson+15

Cold accretion and angular momentum

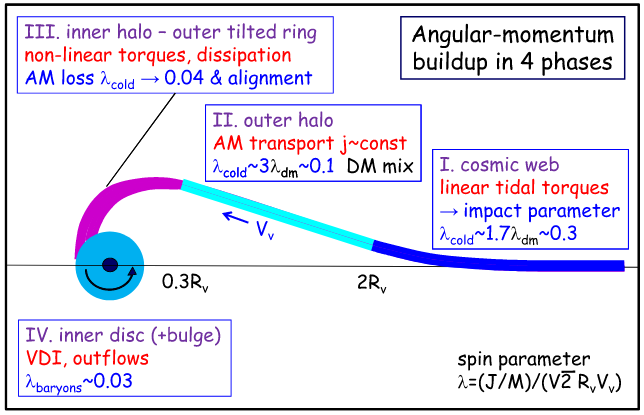
Danovich+15

  1. AM acquisition via TTT >2Rvir
  2. AM transport down to >0.3Rvir
  3. AM loss in inner halo >0.1Rvir
  4. AM loss in inner disk <0.1Rvir

1

2

3

4

Cadiou+ in prep

  • Cause of AM dissipation in internal halo?
    • Gravitational torques? (Danovich+15)
    • Hydrodynamical shock? (Cadiou & Ramsoy, Devriendt+ in prep)
    • AGN/SN feedback? (Nelson+15)
    • KH instability? (Mandelker+18)
  • sAM content of gas just prior to star formation?
  • Alignment of cold flows with large-scale filaments?
    • sAM due to filament "sweep" or impact parameter?
    • Effect of three-filament configuration (Cadiou&Pichon, in prep)

Some open questions / improvements

Thank you

New Horizon simulation, Dubois+ in prep

PS: I am available for a postdoc!

Backup Slides

Galaxy properties

\sim R_\mathrm{vir}

Bulge

\underbrace{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}_{M_\star}

Red or blue?

\frac{v_\mathrm{rot}}{\sigma}

Disk

   

All the properties vary with cosmic time…

Do they vary with spatial location?

 

Galaxies & the cosmic web

Halo model: galaxy properties are inherited from their parent halo + local density (~no effect of the cosmic web)

  • Kaiser bias: large scale overdensities bias halo density


    (Kaiser 84, BBKS 86)
     
  • Spins align with the cosmic web
    (Tempel&Libeskind 13, Codis+15, Chisari+15, ...)
     
  • Galaxy properties are modulated by the cosmic web
    (Laigle+17, Kraljic+18, Musso, Cadiou+18)
n_\mathrm{halo} = b n_\mathrm{DM}

We have to take into account the spatial modulation induced by the cosmic web

 

How do galactic and DM halo scales couple to the large scale anisotropies of the cosmic web?

The Excursion Set Theory

Excursion Set Theory

Galaxy properties & evolution from initial conditions
⇒ Find largest mass that will collapse by z at given location

Large mass                    Small mass

Early collapse

Late collapse

Constrained Excursion Set Theory

+

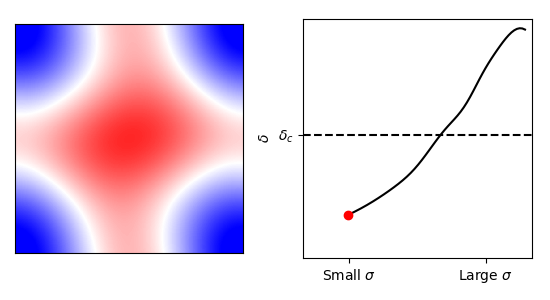
``How does the cosmic web biases the excursion and halo properties?´´

\delta(R) \Rightarrow \delta(R|\vec{r},\mathcal{S}) \quad \sigma(R) \Rightarrow \sigma(R|\vec{r}, \mathcal{S})

The Cosmic Web

How to encode the cosmic web?

Nodes (maxima of density)

Saddle point (center of filament)

Compressing the spatial information

1

2

3

Describe the critical points only

Results

Results

The relevant parameter for quantifying the anisotropy is:

\mathcal{Q} \equiv \frac{r_i\bar{q}_{ij}r_j}{r^2}

Observation (in simu)

v/σ residuals at fixed dens + mass

Theory

But... why?

The filament constrains

  • the density                           
  • the variance of the density

Void         Filament          Void

Conclusion

Conclusions...

  • New model built, room for lots of improvement              
  • Classical results recovered
  • Help to uncover new results


...and perspectives

Towards a more comprehensive halo model

  • How do galaxy respond to large-scale anisotropies?
    ⇒ simulations (WIP)
  • Take into account non spherical collapse (WIP)
  • More subtle quantities:
    • halo merger rate (WIP)
    • halo concentration
    • ... star formation rate?

Excursion set at fixed final mass in different environments

Excursion set at fixed final mass in different environments

Effect of AGN feedback

Simulation Setup

How did the disk acquire its AM?

Requires the knowledge of the Lagrangian evolution of the gas

⇒ now possible using tracer particles

Let look at the filamentary accretion of cold gas at z≥2

Made with Slides.com