Initializing Kernel Adaptive Filters via Probabilistic Inference
Iván Castro, Cristóbal Silva and Felipe Tobar
IEEE-DSP XII August 2017



Overview
- Non linear time series prediction through Kernel Adaptive Filters (KAFs)
- Probabilistic framework for KAF parameters:
- Determine initial conditions
- Construct a fully adaptive parameter-wise KAF
- Prior distributions over parameters:
- Dictionary elements
- Filter weights
- Sparsity focus in parameter estimation
- Non linearity of parameter search is overcome through MCMC optimization
- Validation over synthetic and real world data outperforms standard KAF
Why is non-linear modeling useful?
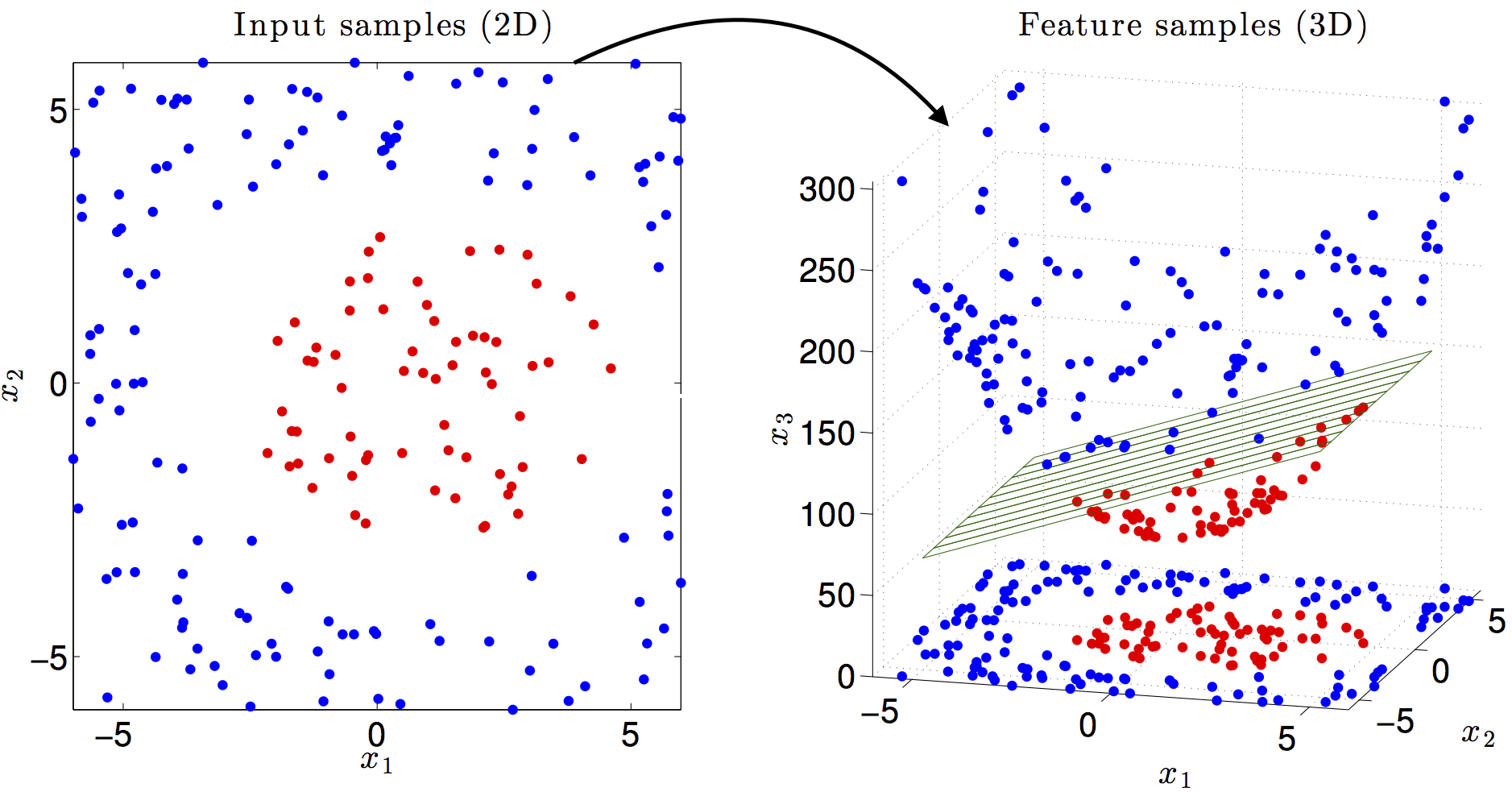
Linearly distributed data
- Well studied problems
- It exists a tremendous variety of tools for different learning topics
Non linearly distributed data
- The problem arises: should we develop new tools, or tinker the existing ones?
- For practical purposes, is easier to adjust the data to the existing tools
- Therefore, feature or space transformations are the answer
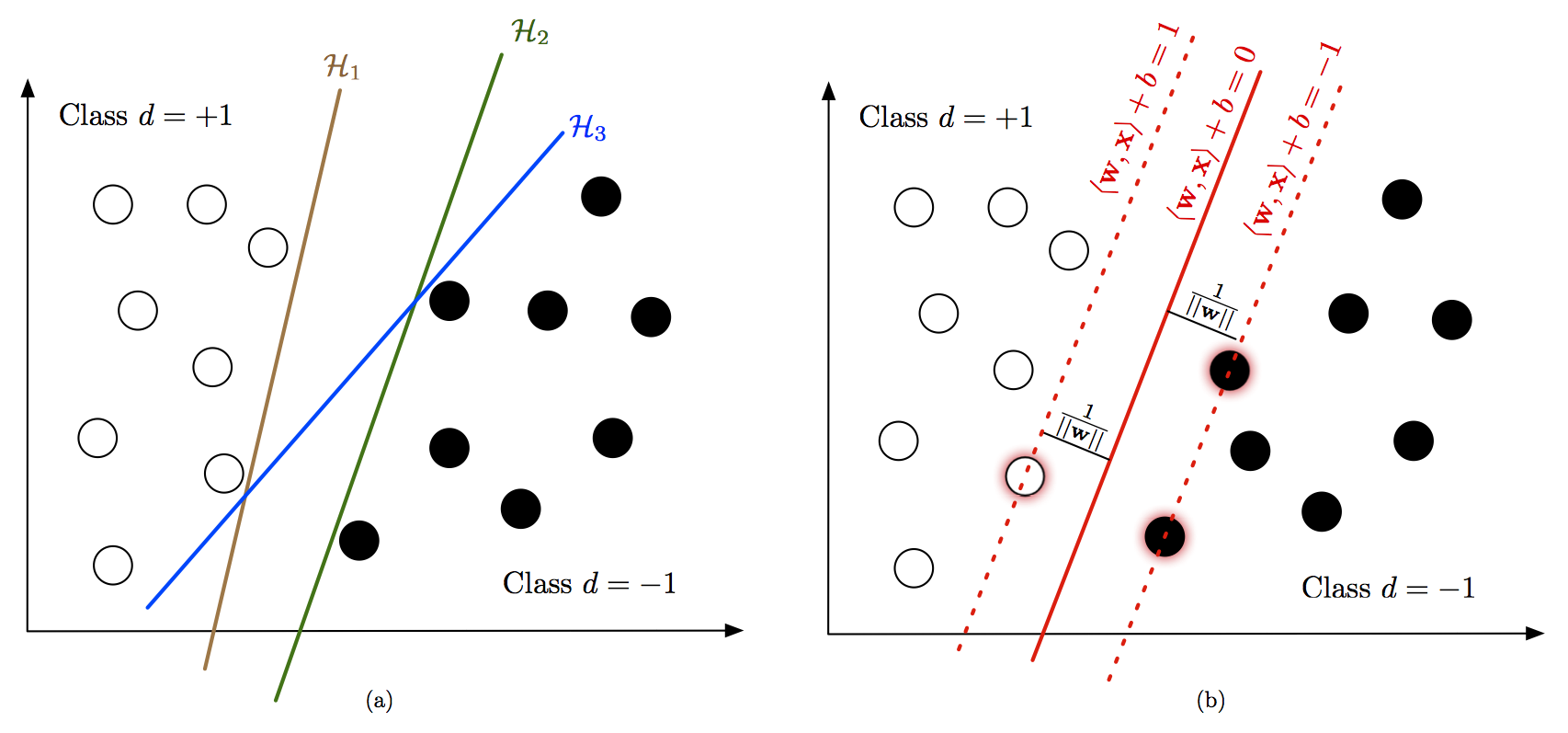
Linear and non-linear estimation
KAFs and PI in a nutshell
Probabilistic Model for KAFs
Probabilistic Model
$$p(Y) = \prod_{i=d}^{N} \frac{1}{2\pi\sigma_{\epsilon}^2} \exp \left( \frac{\left(y - {\alpha}^{\texttt{T}} K_{\sigma_k}\left(x_i, \mathcal{D}\right)\right)^2}{2\sigma_{\epsilon}^2} \right)$$
Model Likelihood
Weights prior
$$p(\alpha) = \frac{1}{\sqrt{2\pi l_{\alpha}^2}} \exp \left( - \frac{\left\| \alpha \right\|^2}{2 l_{\alpha}^2} \right) $$
Sparsity Inducing Prior
$$ p(\mathcal{D}) = \frac{1}{\sqrt{2\pi l_{\mathcal{D}}^2}} \exp \left( - \frac{\left\| K_{\sigma}(\mathcal{D}, \mathcal{D}) \right\|^2}{2 l_{\mathcal{D}}^2} \right)$$
$$ y_i = \sum_{j=1}^{N_i} \alpha_{j} K_{\sigma_k}(i, j) + \epsilon_i $$
Simulations: Lorentz time series offline
\( x[i + 1] = x[i] + dt(\alpha(y[i] - x[i])) \)
\( y[i + 1] = y[i] + dt(x[i](\rho - z[i]) - y[i]) \)
\( z[i + 1] = z[i] + dt(x[i]y[i] - \beta z[i]) \)
Results: anemometer wind series offline
Fully Adaptive Kernel Filtering Online
Analysis of main findings
- Pre-training
- Sparsity inducing prior contribution
- Fully Adaptive KAF
Concluding Remarks
- Probabilistic model improved KAF performance in offline and online applications.
- Further development of online application looks promising.
- MCMC related faster approaches could be explored.
References
[1] W. Liu, P. Pokharel, and J. Principe, “The kernel least-mean-square algorithm,” IEEE Trans. on Signal Process., vol. 56, no. 2, pp. 543–554, 2008.
[2] C. Richard, J. Bermudez, and P. Honeine, “Online prediction of time series data with kernels,” IEEE Trans. on Signal Process., vol. 57, no. 3, pp. 1058 –1067, 2009.