COMP6771

Week 7.2 ⁠— Generic Programming

Concepts

Somewhat more formally, a concept is a description of requriements on one or more types stated in terms of the existence and properties of procedures, type attributes, and type functions defined on the types.

— Elements of Programming, by Alexander Stepanov and Paul McJones.

What's in a requirement?

A constraint is a syntax requirement. The compiler can check these.

An axiom is a semantic requirement. The compiler can't check these, but librarians may assume that they hold true forever. Precondition checks can sometimes check at runtime.

Axioms are usually provided via comments in-tandem with the constraints.

Complexity requirements don't have a fancy name, and can't be checked by the implementation, nor the library author. A sophisticated benchmarking tool might be able to do so.

We say that we satisfy the requirements if all the constraints evaluate as true. We model the concept if, and only if, we satisfy the requirements and meet the axioms and complexity requirements.

Hello, concepts!

template<typename T>
concept type = true;

template<typename T>
requires type<T>
void hello(T)	
{
	std::cout << "Permissive, base-case\n";
}

int main()	
{
	hello(0);
	hello(0.0);
	hello("base-case");	
}

Try it on Compiler Explorer!

Hello, concepts!

template<typename T>
concept type = true;

template<type T> // same as using `typename` right now
void hello(T)
{
	std::cout << "Permissive, base-case\n";
}

int main()	
{
	hello(0);
	hello(0.0);
	hello("base-case");	
}

Try it on Compiler Explorer!

Hello, concepts!

template<typename T>
concept integral = std::is_integral_v<T>;

template<integral T>
void hello(T)
{
	std::cout << "Integral case\n";
}

int main()	
{
	hello(0);
	//hello(0.0);
	//hello("base-case");	
}

Try it on Compiler Explorer!

Hello, concepts!

template<typename T>
concept floating_point = std::is_floating_point_v<T>;

void hello(floating_point auto)
{
   std::cout << "Floating-point case\n";
}

int main()
{
   // hello(0);
   hello(0.0);
   // hello("base case");
}

Try it on Compiler Explorer!

Hello, concepts!

void hello(integral auto)       { std::cout << "Integral case\n";       }
void hello(floating_point auto) { std::cout << "Floating-point case\n"; }
void hello(auto)                { std::cout << "Base-case\n";           }
	
int main()
{
	hello(0);           // prints "Integral case"
	hello(0.0);         // prints "Floating-point case"
	hello("base case"); // prints "Base-case"
}

Try it on Compiler Explorer!

Refining and weakening concepts

A concept C2 refines a concept C1, if whenever C2 is modelled, C1 is also modelled.

A concept C2 weakens C1, if its requirements are a proper subset of C1.

Hello, concepts!

void hello(integral auto) { std::cout << "Integral case\n"; }

template<typename T>
concept signed_integral = integral<T> and std::is_signed_v<T>;

void hello(signed_integral auto) { std::cout << "Signed integral case\n"; }
	
int main()	
{
	hello(0);  // prints "Signed integral case"
	hello(0U); // prints "Integral case"
}

Try it on Compiler Explorer!

signed_integral refines integral

Library concepts

C++20 not only introduced concepts as a language feature, but also three families of highly usable concepts.

Due to many reasons they are available in GCC 10, but not Clang with libc++ (which is what we use in the course).

There's a 1:1 mapping between concepts in range-v3 and what's in the standard library (namespaces aside).

C++ Reference: Concepts library

C++ Reference: Iterators library

Concepts family

Relevant header

<concepts/concepts.hpp>

<range/v3/iterator.hpp>

C++ Reference: Ranges library

<range/v3/range.hpp>

CMakeLists LINK:

range-v3-concepts

range-v3

range-v3

Namespace:

concepts

ranges

ranges

Motivation

struct equal_to {
  template<typename T, typename U>
  auto operator()(T const& t, U const& u) const -> bool
  {
    return t == u;
  }
};

equal_to{}(0, 0)                            // okay, returns true
equal_to{}(std::vector{0}, std::vector{1})  // okay, returns false
equal_to{}(0, 0.0)                          // okay, returns true
equal_to{}(0.0, 0)                          // okay, returns true
equal_to{}(0, std::vector<int>{})           // error: `int == vector` not defined

Motivation

struct equal_to {
  template<typename T, std::equality_comparable_with<T> U>
  auto operator()(T const& t, U const& u) const -> bool
  {
    return t == u;
  }
};

equal_to{}(0, 0)                            // okay, returns true
equal_to{}(std::vector{0}, std::vector{1})  // okay, returns false
equal_to{}(0, 0.0)                          // okay, returns true
equal_to{}(0.0, 0)                          // okay, returns true
equal_to{}(0, std::vector<int>{})           // still error, but makes more sense

Regularity

template<typename T>
concept movable = std::is_object_v<T>
              and std::move_constructible<T>
              and std::assignable_from<T&, T>
              and std::swappable<T>;

template<typename T>
concept copyable = std::copy_constructible<T>
               and std::movable<T>
               and std::assignable_from<T&, T const&>;

template<typename T>
concept semiregular = std::copyable<T> and std::default_initializable<T>;

template<typename T>
concept regular = std::semiregular<T> and std::equality_comparable<T>;

Previously on COMP6771...

A range is an ordered sequence of elements with a designated start and rule for finishing

std::vector<std::string>{"Hello", "world!"}

std::string("Hello, world!")

ℕ ℤ⁺ ℚ⁺ ℝ⁺

Exercise: how can ℂ be made into a range?

for (auto i = 0; std::cin >> i;) { ... }

Iterators and pointers

A pointer is an abstraction of a virtual memory address.

—Sy Brand

Iterators are a generalization of pointers that allow a C++ program to work with different data structures... in a uniform manner.

—Working Draft, Standard for Programming Language C++

Iterators are a family of concepts that abstract different aspects of addresses, ...

—Elements of Programming, Stepanov & McJones

template<typename T, std::equality_comparable_with<T> U>
auto find(std::vector<T> const& r, U const& value) -> std::vector<T>::size_type {
   for (auto i = typename std::vector<T>::size_type{0}; i < r.size(); ++i) {
      if (r[i] == value) {
         return i;
      }
   }
   return r.size();
}

template<typename T, std::equality_comparable_with<T> U>
auto find(std::deque<T> const& r, U const& value) -> std::deque<T>::size_type {
   for (auto i = typename std::deque<T>::size_type{0}; i < r.size(); ++i) {
      if (r[i] == value) {
         return i;
      }
   }
   return r.size();
}

𝑥 sequence containers

𝑦 sequence algorithms (e.g. find)

×

≈

𝑥𝑦 algorithm implementations

We need an intermediate representation

vector

Iterator

Algorithm

Result

Result sink

static vector

string

cord

skip list

linked list

The result may be a one or more iterators, a scalar value, or some combination of both.

𝑥 sequence containers

𝑦 sequence algorithms (e.g. find)

+

≈

𝑥 + 𝑦 total implementations

What makes an iterator tick?

Iterators let us write a generic find

{
  auto const v = std::deque<int>{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
  auto result = ranges::find(v.begin(), v.end(), 6);
  if (result != v.end()) {
    std::cout << "Found 6!\n";
  }
  else {
    std::cout << "Didn't find 6.\n";
  }
}

Iterator invalidation

Iterator is an abstract notion of a pointer
What happens when we modify the container?
- What happens to iterators?
- What happens to references to elements?
Using an invalid iterator is undefined

auto v = std::vector<int>{1, 2, 3, 4, 5};
// Copy all 2s
for (auto it = v.begin(); it != v.end(); ++it) {
  if (*it == 2) {
    v.push_back(2);
  }
}
// Erase all 2s
for (auto it = v.begin(); it != v.end(); ++it) {
  if (*it == 2) {
    v.erase(it);
  }
}

Iterator invalidation - push_back

Think about the way a vector is stored
"If the new size() is greater than capacity() then all iterators and references (including the past-the-end iterator) are invalidated. Otherwise only the past-the-end iterator is invalidated."

auto v = std::vector<int>{1, 2, 3, 4, 5};
// Copy all 2s
for (auto it = v.begin(); it != v.end(); ++it) {
  if (*it == 2) {
    v.push_back(2);
  }
}

https://en.cppreference.com/w/cpp/container/vector/push_back

Iterator invalidation - erase

"Invalidates iterators and references at or after the point of the erase, including the end() iterator."
For this reason, erase returns a new iterator

std::vector v{1, 2, 3, 4, 5};
// Erase all even numbers
for (auto it = v.begin(); it != v.end(); ) {
  if (*it % 2 == 0) {
    it = v.erase(it);
  } else {
    ++it;
  }
}

https://en.cppreference.com/w/cpp/container/vector/erase

Iterator invalidation - general

Containers generally don't invalidate when you modify values
But they may invalidate when removing or adding elements
std::vector invalidates everything when adding elements
std::unordered_(map/set) invalidates all iterators when adding elements
std::map/std::set doesn't invalidate iterators upon insertion (why?)

Iterator adaptors

Wrapper around a type to grant that type iterator properties.

Wrapper around an iterator type to grant additional or different iterator properties.

Example: `std::reverse_iterator`

std::reverse_iterator is an iterator adaptor that transforms an existing iterator's operator++ to mean "move backward" and operator-- to mean "move forward".

std::reverse_iterator<std::vector<int>::iterator>

Readable iterators

Operation

Array-like

Node-based

Iterator

Iteration type

gsl_lite::index

node*

unspecified

Read element

v[i]

i->value

*i

++i

Successor

i = i->next

++i

Advance fwd

j = i + n < ranges::distance(v)
  ? i + n
  : ranges::distance(v);

ranges::next(i, s, n)

j = i->successor(n)

Comparison

i < ranges::distance(v)

i != nullptr

i != s

Indirectly readable

A type I models the concept std::indirectly_readable if:

std::iter_value_t<I>

1. These types exist

std::iter_reference_t<I>

std::iter_rvalue_reference_t<I>

2. These type pairs share a "relationship":

std::iter_value_t<I>&

std::iter_reference_t<I>

std::iter_rvalue_reference_t<I>

std::iter_reference_t<I>

std::iter_rvalue_reference_t<I>

std::iter_value_t<I> const&

A type we can create an lvalue from.

The type I::operator* returns.

The type ranges::iter_move(i) returns.

3. Given an object i of type I , *i outputs the same thing when called with the same input.

// Approximately
std::move(*i)

Generating those iter_ types (preamble)

template<typename T>
class linked_list {
public:
  class iterator;
private:
  struct node {
    T value;
    std::unique_ptr<node> next;
    node* prev;
  };

  std::unique_ptr<node> head_;
};

Generating those iter_ types

template<typename T>
class linked_list<T>::iterator {
public:
  using value_type = T; // std::iter_value_t<iterator> is value_type

  auto operator*() const noexcept -> value_type const& {
     // iter_reference_t<iterator> is value_type&
     // iter_rvalue_reference<iterator> is value_type&&
     return pointee_->value;
  }
private:
  node* pointee_;
  
  friend class linked_list<T>;
  
  explicit iterator(node* pointee)
  : pointee_(pointee) {}
};

static_assert(std::indirectly_readable<linked_list<int>::iterator>);

Weakly incrementable

A type I models the concept std::weakly_incrementable if:

I models std::default_initializable and std::movable
std::iter_difference_t exists and is a signed integer.

Let i be an object of type I.

++i is valid and returns a reference to itself.
i++ is valid and has the same domain as ++i
++i and i++ both advance i, with constant time complexity

Generating `std::iter_difference_t`

template<typename T>
class linked_list<T>::iterator {
public:
  using value_type = T;
  using difference_type = std::ptrdiff_t; // std::iter_difference_t<iterator> is difference_type
  
  iterator() = default;

  auto operator*() const noexcept -> value_type const& { ... }

  auto operator++() -> iterator& {
    pointee_ = pointee_->next.get();
    return *this;
  }
  
  auto operator++(int) -> void { ++*this; }
private:
  //...
};

static_assert(std::weakly_incrementable<linked_list<int>::iterator>);

Iterator basis

A type I models the concept std::input_or_output_iterator if:

std::input_or_output_iterator is the root concept for all six iterator categories.

I models std::weakly_incrementable
*i is a valid expression returns a reference to an object.

Input iterators

A type I models the concept std::input_iterator if:

std::input_iterator describes the requirements for an iterator that can be read from.

I models std::input_or_output_iterator
I models std::indirectly_readable
I::iterator_category is a type alias derived from std::input_iterator_tag

template<std::input_iterator I, typename T>
requires std::indirect_binary_predicate<ranges::equal_to, I, T const*>
auto find(I first, I last, T const& value) -> I {
   for (; first != last; ++first) {
      if (*first == value) {
         return first;
      }
   }
   
   return last;
}

Input iterators let us write an generic find

Checks ranges::equal_to{}(*first, *&value) is possible.

This is how we check *first == value is valid.

Modelling `std::input_iterator`

template<typename T>
class linked_list<T>::iterator {
public:
  using value_type = T;
  using difference_type = std::ptrdiff_t;
  using iterator_category = std::input_iterator_tag;

  iterator() = default;

  auto operator*() const noexcept -> value_type const& { ... }

  auto operator++() -> iterator& { ... }  
  auto operator++(int) -> void { ++*this; }
private:
  //...
};

static_assert(std::input_iterator<linked_list<int>::iterator>);

tl;dr

std::weakly_incrementable

std::indirectly_readable

Requires:

I::difference_type is a signed integer

++i and i++ move i to next element in O(1) time

++i returns a reference to itself

Requires:

I::value_type exists

Type of *i and I::value_type have a type in common

*i always outputs the same thing given the same input

std::input_or_output_iterator

*i return type can be a reference

std::input_iterator

Requires:

I::iterator_category is derived from std::input_iterator_tag

Design problem?

// real find
template<std::input_iterator I, typename T>
auto find(I first, I last, T const& value) -> I;

// bounded find
template<std::input_iterator I, typename T>
auto find_n(I first, std::iter_difference_t<I> n, T const& value) -> I {
   for (; n > 0; ++first, (void)--n) {
      if (*first == value) {
         return first;
      }
   }
   return first;
}

There are >100 algorithms. Do you really want to define copy_n, lower_bound_n, sort_n, etc.?

Counted iterators

// We leverage this through range-v3 in 20T2
// (it's available as std:: in GCC 10)
template<std::input_iterator I>
counted_iterator<I>::counted_iterator(I first, std::iter_difference_t<I> n);

std::ranges::find(
   std::counted_iterator{first, 10},
   ???,
   value)

What's this?

Counted iterators

// We leverage this through range-v3 in 20T2
// (it's available as std:: in GCC 10)
template<std::input_iterator I>
counted_iterator<I>::counted_iterator(I first, std::iter_difference_t<I> n);

std::ranges::find(
   std::counted_iterator{first, 10},
   std::counted_iterator<int>(), // well, that's a bit weird
   value)

It's weird because we are giving meaning to an arbitrary value, and it doesn't really express intentions to the reader.

It's also limiting, because we can't express any additional information. What if we wanted to also stop on the first even int?

Introducing sentinels

A sentinel is a type that denotes the end of a range. It might be an iterator of the same type (like with containers), or it might be a completely different type.

Types S and I model the concept std::sentinel_for<S, I> if:

I models std::input_or_output_iterator
S models std::semiregular

Let i be an object of type I and s be an object of type S.

i == s is well-defined (i.e. it returns bool and we have the other three).
If i != s is true, then i is dereferenceable.

`std::default_sentinel`

std::ranges::find(
   std::counted_iterator{first, 10},
   std::default_sentinel,
   value)

The default sentinel is type-based a way of deferring the comparison rule to the iterator when there's no meaningful definition for an end value.

template<std::input_iterator I>
auto counted_iterator<I>::operator==(std::default_sentinel) const -> bool {
    return n_ == 0;
}

`std::unreachable_sentinel`

The unreachable sentinel is a way of saying "there is no end to this range".

struct unreachable_sentinel_t {
   template<std::weakly_incrementable I>
   friend constexpr bool operator==(unreachable_sentinel_t, I const&) noexcept {
       return false;
   }
};

template<std::input_iterator I, std::sentinel_for<I> S, typename T>
requires std::indirect_binary_predicate<ranges::equal_to, I, T const*>
auto find(I first, S last, T const& value) -> I {
   for (; first != last; ++first) {
      if (*first == value) {
         return first;
      }
   }
   
   return first;
}

Completing our implementation of find

Relationship between iterators and ranges

Let's say there's an object r of type R

`std::ranges::begin`

template<typename R> std::input_or_output_iterator auto std::ranges::begin(R&& r);

Returns an object that models std::input_or_output_iterator.

Works on lvalues and sometimes on rvalues.

Works on types that use r.begin() (e.g. std::vector)

Works on types that use begin(r) without needing to do this insanity in every scope:

using std::begin;
auto i = begin(r);

Example usage:

auto i = std::ranges::begin(r);

std::iterator_t<R> is defined as the deduced return type for std::ranges::begin(r).

`std::ranges::end`

template<typename R> std::sentinel_for<std::ranges::iterator_t<R>> auto std::ranges::end(R&& r);

Returns an object that models std::sentinel_for<std::iterator_t<R>>.

Works on lvalues and sometimes on rvalues.

Works on types that use r.end() (e.g. std::vector)

Works on types that use end(r) without needing to do this insanity in every scope:

using std::end;
auto i = end(r);

Example usage:

auto s = std::ranges::end(r);

std::sentinel_t<R> is defined as the deduced return type for std::ranges::end(r).

`std::ranges::range`

template<typename T>
concept range = requires(R& r) {
   std::ranges::begin(r); // returns an iterator
   std::ranges::end(r);   // returns a sentinel for that iterator
};

R models the concept range when:

R is a valid type parameter for both std::ranges::begin and std::ranges::end, where std::ranges::end
ranges::begin(r) returns an iterator in amortised O(1) time.
ranges::end(r) returns a sentinel in amortised O(1) time.
[ranges::begin(r), ranges::end(r)) denotes a valid range (i.e. there's a finite number of iterations between the two).

Note: std::ranges::begin(r) is not required to return the same result on each call.

`std::ranges::input_range`

Refines range to make sure ranges::begin(r) returns an input iterator.

template<typename T>
concept input_range =
   std::ranges::range<T> and
   std::input_iterator<std::ranges::iterator_t<T>>;

A range-based find

template<ranges::input_range R, typename T>
requires std::indirect_binary_predicate<ranges::equal_to,
                                        ranges::iterator_t<R>>, const T*>
auto find(R&& r, const T& value) -> ranges::borrowed_iterator_t<R> {
   return comp6771::find(ranges::begin(r), ranges::end(r), value)
}

The range-based find simply defers to the iterator-based find. We prefer this algorithm when we need both begin and end, as opposed to arbitrary iterators, so that we don't mix iterators up and create invalid ranges (it's also more readable).

ranges::borrowed_iterator_t<R> is the same as ranges::iterator_t<R> if R is an lvalue reference or a reference to a borrowed range (not discussed), and a non-iterator otherwise.

auto v = std::vector<int>{0, 1, 2, 3};
ranges::find(v, 2); // returns an iterator
ranges::find(views::iota(0, 100), 2); // returns an iterator

ranges::find(std::vector<int>{0, 1, 2, 3}, 2); // returns ranges::dangling which is more useful
                                               // than void (better compile-time diagnostic info)

Turning our list into a range

template<typename T>
class linked_list {
public:
  class iterator;
  
  auto begin() const -> iterator { return head_; }
  auto end() const -> iterator { return tail_; }
private:
  struct node {
    T value;
    std::unique_ptr<node> next;
    node* prev;
  };

  std::unique_ptr<node> head_;
  node* tail_;
};

Find last

template<std::input_iterator I, std::sentinel_for<I> S, class Val>
requires std::indirect_relation<ranges::equal_to, I, Val const*>
auto find_last(I first, S last, Val const& value) -> I {
	auto cache = std::optional<I>();
	for (; first != last; ++first) {
		if (*first == value) {
			cache = first;
		}
	}

	return cache.value_or(std::move(first));
}

I isn't guaranteed to model std::copyable

Even if it were, I is only guaranteed to work for a single-pass

What if we are reading input from a network socket?

Incrementable

A type I models the concept std::incrementable if:

I models std::weakly_incrementable
I models std::regular
i++ is equivalent to

auto I::operator++(int) -> I {
   auto temp = i;
   ++i;
   return temp;
}

Refines std::weakly_incrementable so you can copy and iterate over the same sequence of values multiple times.

Modelling `std::incrementable`

template<typename T>
class linked_list<T>::iterator {
public:
  using value_type = T;
  using difference_type = std::ptrdiff_t;
  using iterator_category = std::input_iterator_tag;

  iterator() = default;

  auto operator*() const noexcept -> value_type const& { ... }

  auto operator++() -> iterator& { ... }  
  auto operator++(int) -> iterator {
     auto temp = *this;
     ++*this;
     return temp;
  }
private:
  //...
};

static_assert(std::incrementable<linked_list<int>::iterator>);

Forward iterators

A type I models the concept std::forward_iterator if:

I models std::input_iterator
I models std::incrementable
I::iterator_category is derived from std::forward_iterator_tag
I can be its own sentinel

Refines input iterators so you can copy and iterate over the same sequence of values multiple times.

Modelling `std::forward_iterator`

template<typename T>
class linked_list<T>::iterator {
public:
  using value_type = T;
  using difference_type = std::ptrdiff_t;
  using iterator_category = std::forward_iterator_tag;

  iterator() = default;

  auto operator*() const noexcept -> value_type& { ... }

  auto operator++() -> iterator& { ... }  
  auto operator++(int) -> iterator { ... }
  
  auto operator==(iterator const&) const -> bool = default;
private:
  //...
};

static_assert(std::forward_iterator<linked_list<int>::iterator>);

Find last

template<std::forward_iterator I, std::sentinel_for<I> S, class Val>
requires std::indirect_relation<ranges::equal_to, I, Val const*>
auto find_last(I first, S last, Val const& value) -> I {
	auto cache = std::optional<I>();
	for (; first != last; ++first) {
		if (*first == value) {
			cache = first;
		}
	}

	return cache.value_or(std::move(first));
}

Can we optimise this algorithm further?

Forward range

Refines input_range to make sure ranges::begin(r) returns a forward iterator.

template<typename T>
concept forward_range =
   std::ranges::input_range<T> and
   std::forward_iterator<std::ranges::iterator_t<T>>;

ranges::begin(r) now returns the same value given the same input.

tl;dr

std::input_iterator

std::incrementable

Requires:

std::weakly_incrementable

std::regular

auto I::operator++(int) -> I {
   auto temp = *this;
   ++*this;
   return temp;
}

std::forward_iterator

(See previous tl;dr)

I::iterator_category is derived from std::forward_iterator_tag

Requires:

auto operator==(I, I) -> bool;

auto operator!=(I, I) -> bool; (before C++20)

Bidirectional iterators

A type I models the concept std::bidirectional_iterator if:

I models std::forward_iterator
I::iterator_category is derived from std::bidirectional_iterator_tag
--i is valid and returns a reference to itself.
i-- is valid and has the same domain as --i
--i and i-- both decline i in constant time complexity
i-- is equivalent to

Refines forward iterators so you can iterate in reverse order.

auto I::operator--(int) -> I {
   auto temp = i;
   --i;
   return temp;
}

Modelling `std::bidirectional_iterator`

template<typename T>
class linked_list<T>::iterator {
public:
  using value_type = T;
  using difference_type = std::ptrdiff_t;
  using iterator_category = std::bidirectional_iterator_tag;

  iterator() = default;

  auto operator*() const noexcept -> value_type const& { ... }

  auto operator++() -> iterator& { ... }  
  auto operator++(int) -> iterator { ... }
  
  auto operator--() -> iterator& {
     pointee_ = pointee_->prev;
     return *this;
  }
  
  auto operator--(int) -> iterator {
     auto temp = *this;
     --*this;
     return temp;
  }
  
  auto operator==(iterator const&) const -> bool = default;
private:
  //...
};

static_assert(std::bidirectional_iterator<linked_list<int>::iterator>);

Find last

template<std::bidirectional_iterator I, class Val>
requires std::indirect_relation<ranges::equal_to, I, Val const*>
auto find_last(I first, I last, Val const& value) -> I {
	while (first != last) {
		--last;
		if (*last == value) {
			return last;
		}
	}

	return first;
}

We keep both implementations

template<std::forward_iterator I, std::sentinel_for<I> S, class Val>
requires std::indirect_relation<ranges::equal_to, I, Val const*>
auto find_last(I first, S last, Val const& value) -> I {
	auto cache = std::optional<I>();
	for (; first != last; ++first) {
		if (*first == value) {
			cache = first;
		}
	}

	return cache.value_or(std::move(first));
}

template<std::bidirectional_iterator I, class Val>
requires std::indirect_relation<ranges::equal_to, I, Val const*>
auto find_last(I first, I last, Val const& value) -> I {
	while (first != last--) {
		if (*last == value) {
			return last;
		}
	}

	return first;
}

tl;dr

std::forward_iterator

auto I::operator--(int) -> I {
   auto temp = *this;
   --*this;
   return temp;
}

std::bidirectional_iterator

(See previous tl;dr)

I::iterator_category is derived from std::bidirectional_iterator_tag

Requires:

--i and i-- move to the previous element, with O(1) time complexity

--i returns a reference to itself

A new example type

Our linked_list has been a good friend up until now.

It's sadly run its course for the lecture content and we can't use it any more.

Let's now define something similar to ranges::views::iota

`simple_iota_view`

template<std::integral I>
class simple_iota_view {
   class iterator;
public:
   simple_iota_view() = default;
   
   simple_iota_view(I first, I last)
   : start_(std::move(first))
   , stop_(std::move(last)) {}

   auto begin() const -> iterator { return iterator(*this, start_); }
   auto end() const -> iterator { return iterator(*this, stop_); }
private:
   I start_ = I();
   I stop_ = I();
};

`simple_iota_view::iterator`

template<std::integral I>
class simple_iota_view<I>::iterator {
public:
   using value_type = I;
   using difference_type = std::iter_difference_t<I>;
   using iterator_category = iterator_category_helper_t<I>;

   iterator() = default;
   
   explicit iterator(simple_iota_view const& base, I const& value)
   : base_(std::addressof(base))
   , current_(value) {}

   auto operator*() const -> I { return current_; }

   auto operator++() -> iterator& { ++current_; return *this; }
   auto operator++(int) -> iterator { ... }
   
   auto operator--() -> iterator& { --current_; return *this; }
   auto operator--(int) -> iterator { ... }
   
   auto operator==(iterator) const -> bool = default;
private:
   simple_iota_view const* base_ = nullptr;
   I current_ = I();
};

Check if two ranges meet some predicate, element-wise

template<std::input_iterator I1, std::sentinel_for<I1> S1,
         std::input_iterator I2, std::sentinel_for<I2> S2,
         std::indirect_binary_predicate<Pred, I1, I2> Pred = ranges::equal_to>
bool comp6771::equal(I1 first1, S1 last1, I2 first2, S2 last2, Pred pred = {})
{
   auto result = ranges::mismatch(std::move(first1), last1,
                                  std::move(first2), last2,
                                  std::ref(pred));
   return (result.in1 == last1) and (result.in2 == last2);
	
}

A good starting point, but ranges::mismatch isn't designed to short-circuit.

What might we be able to do to optimise this?

An optimisation

template<std::input_iterator I1, std::sentinel_for<I1> S1,
         std::input_iterator I2, std::sentinel_for<I2> S2,
         std::indirect_binary_predicate<Pred, I1, I2> Pred = ranges::equal_to>
bool comp6771::equal(I1 first1, S1 last1, I2 first2, S2 last2, Pred pred = {})
{
   auto result = ranges::mismatch(std::move(first1), last1,
                                  std::move(first2), last2,
                                  std::ref(pred));
   return (result.in1 == last1) and (result.in2 == last2);
	
}

If ranges don't have the same distance, then complexity should be constant!

Checking the distance of a range is currently a linear operation...

Sized sentinels

Refines std::sentinel so that we can compute the distance between two elements in constant time.

Given an iterator type I, A type S models the concept std::sized_sentinel_for if:

S models std::sentinel_for
ranges::disable_sized_sentinel_for<S, I> is false
s - i returns the number of elements between the iterator and sentinel, as an object of type std::iter_difference_t, in constant time
i - s is equivalent to -(s - i)

Used to opt out of being a sized sentinel for I if s - i doesn't evaluate in O(1) time (i.e. this is false by default).

An optimisation

template<std::input_iterator I1, std::sentinel_for<I1> S1,
         std::input_iterator I2, std::sentinel_for<I2> S2,
         std::indirect_binary_predicate<Pred, I1, I2> Pred = ranges::equal_to>
bool comp6771::equal(I1 first1, S1 last1, I2 first2, S2 last2, Pred pred = {})
{
   if constexpr (std::sized_sentinel_for<S1, I1> and std::sized_sentinel_for<S2, I2>) {
      if (last1 - first1 != last2 - first2) {
         return false;
      }
   }

   auto result = ranges::mismatch(std::move(first1), last1,
                                  std::move(first2), last2,
                                  std::ref(pred));
   return (result.in1 == last1) and (result.in2 == last2);
	
}

Modelling `std::sized_sentinel_for<S, I>`

template<std::integral I>
class simple_iota_view<I>::iterator {
public:
   using value_type = I;
   using difference_type = std::iter_difference_t<I>;
   using iterator_category = iterator_category_helper_t<I>;

   iterator() = default;
   
   explicit iterator(simple_iota_view const& base, I const& value);

   auto operator*() const -> I;
   auto operator++() -> iterator&;
   auto operator++(int) -> iterator;
   auto operator--() -> iterator&;
   auto operator--(int) -> iterator;
   
   auto operator==(iterator) const -> bool = default;
   
   friend auto operator-(iterator const x, iterator const y) -> difference_type {
     assert(x.base_ == y.base_);
     return x.current_ - y.current_;
   }
private: // ...
};
static_assert(std::sized_sentinel_for<simple_iota_view<int>::iterator, simple_iota_view<int>::iterator>);

Partition point

0 2 7 6 8 1 3 7 5

^

template<std::forward_iterator I, std::sentinel_for<I> S,
         std::indirect_unary_predicate<I> Pred>
auto partition_point(I first, S last, Pred pred) -> I {
   auto end = ranges::next(first, last);
   while (first != end) {
      auto middle = ranges::next(first, ranges::distance(first, end) / 2);
      if (std::invoke(pred, *middle)) {
         first = std::move(middle);
         ++first;
         continue;
      }
      end = std::move(middle);
   }
   
   return first;
}

Partition point

What is the complexity of this partition_point?

O(log(last - first)) applications of pred

Partition point complexity

O(log(last - first)) applications of pred

But there's currently O(n) steps through the range.

Wouldn't it be great for the applications and steps to be the same?

Random-access iterators

A type I models the concept std::random_access_iterator if:

I models std::bidirectional_iterator
I::iterator_category is derived from std::random_access_iterator_tag
I models std::totally_ordered
I is a sized sentinel for itself

Let i and j be objects of type I and n be an object of type iter_difference_t.

i += n and i -= n are valid and return references to the same object.
i ±= n advances/declines i by n elements in constant time.
j ± n advances/declines a copy of j by n elements in constant time.
n + j is the same as j + n.
j[n] is the same as *(j + n).

Refines bidirectional iterators so you can make arbitrary steps in constant time

Modelling `std::random_access_iterator`

template<std::integral I>
class simple_iota_view<I>::iterator {
public:
   using value_type = I;
   using difference_type = std::iter_difference_t<I>;
   using iterator_category = std::random_access_iterator_tag;

   // stuff from previous slides

   auto operator<=>(iterator) const -> std::strong_ordering = default;
   
   auto operator+=(difference_type const n) -> iterator& {
      current_ += n;
      return *this;
   }
   
   auto operator-=(difference_type const n) -> iterator& { return *this += -n; }
   auto operator[](difference_type const n) const -> value_type { return *(*this + n); }

   friend auto operator+(iterator j, difference_type const n) -> iterator { return j += n; }
   friend auto operator+(difference_type const n, iterator j) -> iterator { return j += n; }
   friend auto operator-(iterator j, difference_type const n) -> iterator { return j -= n; }
   friend auto operator-(iterator const x, iterator const y) -> difference_type { ... }
};

static_assert(std::random_access_iterator<simple_iota_view<int>::iterator>);

tl;dr

std::bidirectional_iterator

std::random_access_iterator

(See previous tl;dr)

Requires:

std::sized_sentinel_for<I, I>

Requires:

std::sentinel_for<I, I>

std::disable_sentinel_for<I, I> == false

s - i returns the number of elements between i and s in O(1) time

i - s is equivalent to s - i

I::iterator_category is derived from std::random_access_iterator_tag

i += n and i -= n advance/decline i by n elements in O(1) time

j + n, n + j and j - n advance/decline a copy of j by n elements in O(1) time

j[n] is equivalent to *(j + n)

std::totally_ordered (i.e. has all traditional comparison operators)

What happens if we want to write to a range?

template<std::input_iterator I, std::sentinel_for<I> S,
         ??? O>
auto copy(I first, S last, O result) -> copy_result<I, O> {
   for (; first != last; ++first, (void)++result) {
      *result = *first;
   }
   return {std::move(first), std::move(result)};
}

What do O and I need to model?

template<typename T,
         ??? O,
         std::sentinel_for<O> S>
auto fill(O first, S last, T const& value) -> O {
   for (first != last) {
      *first++ = value;
   }
   return first;
}

What does O need to model?

Writable iterators

Operation

Array-like

Node-based

Iterator

Iteration type

gsl_lite::index

node*

unspecified

Write to element

v[i] = x

i->value = x

*i = x

++i

Successor

i = i->next

++i

Advance fwd

j = i + n < ranges::distance(v)
  ? i + n
  : ranges::distance(v);

ranges::next(i, s, n)

j = i->successor(n)

Comparison

i < ranges::distance(v)

i != nullptr

i != s

Indirectly writable

Let o be a possibly-constant object of type O and val be an object of type T. A type O models the concept std::indirectly_writable<T> if:

*o = val is possible regardless of whether O is const-qualified
These expressions are possible for O& and O&&:
- *o = std::move(val)
- *std::move(o) = std::move(val)
All forms of *o = val result in *o returning a reference.

The concept indirectly_writable determines if we can write a value to whatever the iterator is referencing.

Modelling `std::indirectly_writable<O, T>`

template<typename T>
class linked_list<T>::iterator {
public:
  using value_type = T;
  using difference_type = std::ptrdiff_t;
  using iterator_category = std::bidirectional_iterator_tag;

  iterator() = default;

  auto operator*() const noexcept -> value_type& { return pointee_->data; }

  auto operator++() -> iterator& { ... }  
  auto operator++(int) -> iterator { ... }
  auto operator--() -> iterator& { ... }
  auto operator--(int) -> iterator { ... }
  
  auto operator==(iterator) const -> bool = default;
private:
  //...
};

static_assert(std::indirectly_writable<linked_list<int>::iterator, int>);

Applying this to copy

template<std::input_iterator I, std::sentinel_for<I> S,
         std::weakly_incrementable O>
requires std::indirectly_copyable<I, O>
auto copy(I first, S last, O result) -> copy_result<I, O> {
   for (; first != last; ++first, (void)++result) {
      *result = *first;
   }
   return {std::move(first), std::move(result)};
}

Where std::indirectly_copyable<I, O> means "we can copy the value we've read from I into O". In other words:

template<typename In, typename Out>
concept indirectly_copyable =
   std::indirectly_readable<In> and
   std::indirectly_writable<Out, std::iter_reference_t<In>>;

Output iterators

Let o be a possibly-constant object of type O and val be an object of type T. A type O models the concept std::output_iterator<T> if:

O models std::input_or_output_iterator
O models std::indirectly_writable<T>
- *(o++) = val is valid, if T is an lvalue, and is equivalent to
```
    *o = val;
    ++o;
```
- *(o++) = std::move(val) is valid, if T is an rvalue, and is equivalent to
```
    *o = std::move(val);
    ++o;
```

The concept output_iterator refines the base iterator concept by requiring the iterator models indirectly_writable.

Modelling `std::output_iterator<O, T>`

template<typename T>
class linked_list<T>::iterator {
public:
  // ...
private:
  //...
};

static_assert(std::bidirectional_iterator<linked_list<int>::iterator>);
static_assert(std::output_iterator<linked_list<int>::iterator, int>);

Iterators that model both std::bidirectional_iterator and std::indirectly_writable<O, T> model std::output_iterator<O, T> by default.

There isn't a concept for these kinds of iterators, but they're known as mutable iterators in generic programming theory.

Applying this to fill

template<typename T,
         std::output_iterator<T const&> O,
         std::sentinel_for<O> S>
auto fill(O first, S last, T const& value) -> O {
   while (first != last)
      *first++ = value;
   }
   return first;
}

Non-mutable output iterators are write-once-then-advance.

Iterators and `const`

Mutable iterators are always indirectly_writable, even when const-qualified.

void write_access(linked_list<int>::iterator const i) {
   *i = 42; // okay, changes what *i refers to
   i = {}; // error: can't change i itself
}

This is the same problem as T* const: we have a constant iterator, not an iterator pointing-to-const.

`const_iterator`s

A const_iterator is the iterator-equivalent of T const*.

void no_write_access(linked_list<int>::const_iterator i) {
   i = {}; // okay

   *i = 42; // error: can't indirectly write to i
}

How do we make `const_iterator`s?

Attempt 1: Two types

template<typename T>
class linked_list<T>::iterator {
public:
  using value_type = T;
  using difference_type = std::ptrdiff_t;
  using iterator_category = std::bidirectional_iterator_tag;

  iterator() = default;

  auto operator*() const noexcept -> value_type& {
     return pointee_->data;
  }

  auto operator++() -> iterator& { ... }  
  auto operator++(int) -> iterator { ... }
  auto operator--() -> iterator& { ... }
  auto operator--(int) -> iterator { ... }
  
  auto operator==(iterator) const -> bool = default;
private:
  //...
};

static_assert(
   std::indirectly_writable<linked_list<int>::iterator, int>);

template<typename T>
class linked_list<T>::const_iterator {
public:
  using value_type = T;
  using difference_type = std::ptrdiff_t;
  using iterator_category = std::bidirectional_iterator_tag;

  iterator() = default;

  auto operator*() const noexcept -> value_type const& {
     return pointee_->data;
  }

  auto operator++() -> iterator& { ... }  
  auto operator++(int) -> iterator { ... }
  auto operator--() -> iterator& { ... }
  auto operator--(int) -> iterator { ... }
  
  auto operator==(iterator) const -> bool = default;
private:
  //...
};

static_assert(
   not std::indirectly_writable<linked_list<int>::const_iterator,
                                int>);

Why might this be a bad approach?

Attempt 2: Parameterise on constness

template<typename T>
class linked_list {
  template<bool is_const>
  class iterator_impl;
public:
  using iterator = iterator_impl<false>;
  using const_iterator = iterator_impl<true>;
  
  // ...
};

We define one template class iterator_impl and parameterise it based on constness.

Then we add metadata to iterator_impl to help it understand what is_const means.

Attempt 2: Parameterise on constness

template<typename T>
template<bool is_const>
class linked_list<T>::iterator_impl {
public:
  using value_type = T;
  using difference_type = std::ptrdiff_t;
  using iterator_category = std::bidirectional_iterator_tag;

  iterator_impl() = default;
  
  auto operator*() const noexcept -> value_type const&
  requires is_const {
     return pointee_->data;
  }

  auto operator*() const noexcept -> value_type&
  requires (not is_const) {
     return pointee_->data;
  }

  auto operator++() -> iterator_impl& { ... }  
  auto operator++(int) -> iterator_impl { ... }
  auto operator--() -> iterator_impl& { ... }
  auto operator--(int) -> iterator_impl { ... }
  auto operator==(iterator_impl) const -> bool = default;
private:
  maybe_const_t<is_const, T>* pointee_;
  
  iterator_impl(maybe_const_t<is_const, T>* ptr) { ... }
  friend class linked_list<T>;
};

template<bool is_const, typename T>
struct maybe_const {
  using type = T;
};

template<typename T>
struct maybe_const<true, T> {
  using type = T const;
};

template<bool is_const, typename T>
using maybe_const_t =
   typename maybe_const<is_const, T>;

This is partial template specialisation, which we cover in Week 8. For now, you can think of it like a switch on constness, based on some compile-time property.

Getting the right kind of iterator

template<typename T>
class linked_list {
  template<bool is_const>
  class iterator_impl;
public:
  using iterator = iterator_impl<false>;
  using const_iterator = iterator_impl<true>;
  
  auto begin() -> iterator { return iterator(head_); }
  auto end() -> iterator { return iterator(tail_); }
  
  auto begin() const -> const_iterator { return iterator(head_); }
  auto end() const -> const_iterator { return iterator(tail_); }
};

Either way, you'll need to have two overloads for begin and for end. We don't want linked_list<int> const to return mutable iterators!

How might you improve this code?

Getting the right kind of iterator DRY style

template<typename T>
class linked_list {
public:
  using iterator = iterator_impl<false>;
  using const_iterator = iterator_impl<true>;
  
  auto begin() -> iterator { begin_impl(*this); }
  auto end() -> iterator { return end_impl(*this); }
  
  auto begin() const -> const_iterator { return begin_impl(*this); }
  auto end() const -> const_iterator { return end_impl(*this); }
private:
  template<typename T>
  static auto begin_impl(T& t) -> decltype(t.begin()) {
    return iterator_impl<std::is_const_v<T>>(head_);
  }
  
  template<typename T>
  static auto end_impl(T& t) -> decltype(t.end()) {
    return iterator_impl<std::is_const_v<T>>(tail_);
  }
};

When to have differently-qualified overloads

Is the iterator indirectly_writable?

Then you should use

Yes

begin() const end() const

begin() end()

No, but the range does housekeeping (e.g. keeps a cache)

begin() end()

What about `cbegin` and `cend`?

Standard containers ship with cbegin and cend as member functions.

While they might be handy, they're not necessary.

ranges::cbegin(r) and ranges::cend(r)will Do The Right Thing™ if you have a const-qualified begin member function. (Try it on our linked_list and see if it works!)

Not all ranges will have cbegin/cend member functions, so the only reliable way to get an iterator to a constant range is to use one of the above.

`rbegin` and `rend`

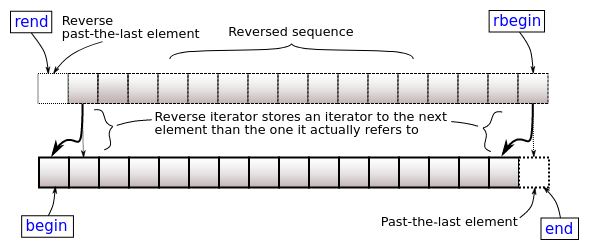
rbegin and rend idiomatically return reverse_iterator<iterator>s.

Unlike cbegin/cend, you'll probably want to define rbegin/rend as members for backwards-compatibility reasons.

crbegin/crend are in the same category as cbegin/cend.

Video Resources

Generic Programming, by Sean Parent

Concepts in 60: Everything You Need to Know and Nothing You Don't, by Andrew Sutton
Concepts: A Day in the Life, by Saar Raz
An Overview of Standard Ranges, by Tristan Brindle
Algorithm Intuition, by Conor Hoekstra
Range Algorithms, Views and Actions: A Comprehensive Guide, by Dvir Yitzchacki
From STL to Ranges: Using Ranges Effectively, by Jeff Garland
What a View! Building Your own (Lazy) Range Adaptors, by Christopher Di Bella

Written Resources

From Mathematics to Generic Programming, by Alexander Stepanov and Daniel Rose

Elements of Programming, by Alexander Stepanov and Paul McJones

COMP6771

Week 7.2 ⁠— Generic Programming

Concepts

What's in a requirement?

Hello, concepts!

Hello, concepts!

Hello, concepts!

Hello, concepts!

Hello, concepts!

Refining and weakening concepts

Hello, concepts!

Library concepts

Motivation

Motivation

Regularity

Previously on COMP6771...

A range is an ordered sequence of elements with a designated start and rule for finishing

Iterators and pointers

𝑥 sequence containers

𝑦 sequence algorithms (e.g. find)

×

≈

𝑥𝑦 algorithm implementations

We need an intermediate representation

𝑥 sequence containers

𝑦 sequence algorithms (e.g. find)

+

≈

𝑥 + 𝑦 total implementations

What makes an iterator tick?

Iterators let us write a generic find

Iterator invalidation

Iterator invalidation - push_back

Iterator invalidation - erase

Iterator invalidation - general

Iterator adaptors

Example: std::reverse_iterator

Readable iterators

Generating those iter_ types (preamble)

Generating those iter_ types

Generating std::iter_difference_t<I>

Input iterators let us write an generic find

Modelling std::input_iterator<I>

tl;dr

Design problem?

Counted iterators

Counted iterators

Completing our implementation of find

Relationship between iterators and ranges

A range-based find

Turning our list into a range

Find last

Modelling std::incrementable<I>

Modelling std::forward_iterator<I>

Find last

tl;dr

Modelling std::bidirectional_iterator<I>

Find last

We keep both implementations

tl;dr

A new example type

simple_iota_view

simple_iota_view::iterator

Check if two ranges meet some predicate, element-wise

An optimisation

An optimisation

Modelling std::sized_sentinel_for<S, I>

Partition point

Partition point

Partition point complexity

Modelling std::random_access_iterator<I>

tl;dr

What happens if we want to write to a range?

Writable iterators

Modelling std::indirectly_writable<O, T>

Applying this to copy

Modelling std::output_iterator<O, T>

Applying this to fill

Iterators and const

const_iterators

Example: `std::reverse_iterator`

Generating `std::iter_difference_t<I>`

Modelling `std::input_iterator<I>`

Modelling `std::incrementable<I>`

Modelling `std::forward_iterator<I>`

Modelling `std::bidirectional_iterator<I>`

`simple_iota_view`

`simple_iota_view::iterator`

Modelling `std::sized_sentinel_for<S, I>`

Modelling `std::random_access_iterator<I>`

Modelling `std::indirectly_writable<O, T>`

Modelling `std::output_iterator<O, T>`

Iterators and `const`

`const_iterator`s

How do we make `const_iterator`s?

What about `cbegin` and `cend`?

`rbegin` and `rend`