Applied Measure Theory
for Probabilistic Modeling
Chad Scherrer
July 2021

Introduction: Post-Covid Travel Planning




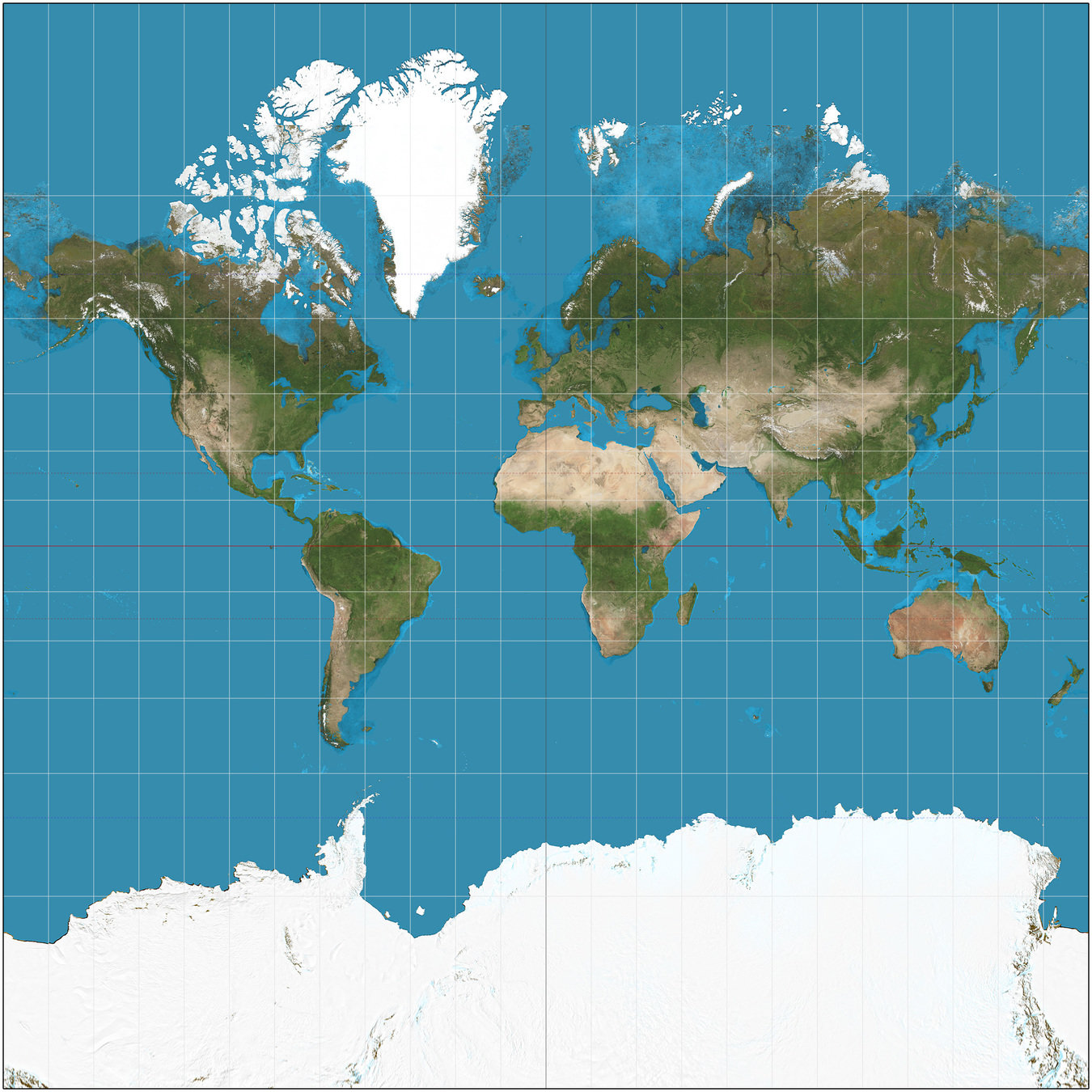



- Choose a destination "randomly"
- Your choice of map matters!
- One perspective:
-
Transform the "dart distribution" to a distribution on the globe
-
Transform the "dart distribution" to a distribution on the globe
- Our perspective for today:
- Transform "uniform on the globe" to a measure on a map
-
Consider our "dart distribution" using this as a base measure
-
Work with measures in terms of relative densities
Toy Problem: Approximating Beta(1.5,4)

Find a Normal distribution to approximate p = Beta(1.5, 4)
Standard Normal
density(Normal(), x)logdensity(::Normal{()} , x) = - x^2 / 2
Standard Normal
density(Normal(), x)logdensity(::Normal{()} , x) = - x^2 / 2
basemeasure(::Normal{()}) = (1/sqrt2π) * Lebesgue(ℝ)

density(Normal(), Lebesgue(ℝ), x)
A Different Parameterization
A measure can have multiple parameterizations
Here (μ, logσ) allows use of parameters from ℝ²
q(θ) = Normal(μ=θ[1], logσ=θ[2])function logdensity(d::Normal{(:μ,:logσ)}, x)
μ, logσ = d.μ, d.logσ
return -logσ - 0.5(exp(-2logσ) * (x - μ) ^ 2)
end
Computing the KL Divergence
D_\text{KL}(p || q) = \mathbb{E}_p[\log p - \log q]
p = Beta(1.5, 4)
q(θ) = Normal(μ=θ[1], logσ=θ[2])logdensity(p, q, x)\underbrace{\hspace{1in}}
Minimizing the KL Divergence
julia> using Symbolics; @variables μ logσ x;
Minimizing the KL Divergence
julia> using Symbolics; @variables μ logσ x;
julia> ℓ = logdensity(p, q([μ,logσ]), x)
3.2 + logσ + 0.5log(x) + 3log(1 - x) + 0.5exp(-2logσ)*((x - μ)^2)
Minimizing the KL Divergence
julia> using Symbolics; @variables μ logσ x;
julia> ℓ = logdensity(p, q([μ,logσ]), x)
3.2 + logσ + 0.5log(x) + 3log(1 - x) + 0.5exp(-2logσ)*((x - μ)^2)
julia> Symbolics.derivative(ℓ,μ)
0.5exp(-2logσ)*(2μ - (2x))
\mu = \mathbb{E}_p[x] \approx 0.27
Minimizing the KL Divergence

julia> using Symbolics; @variables μ logσ x;
julia> ℓ = logdensity(p, q([μ,logσ]), x)
3.2 + logσ + 0.5log(x) + 3log(1 - x) + 0.5exp(-2logσ)*((x - μ)^2)
julia> Symbolics.derivative(ℓ,μ)
0.5exp(-2logσ)*(2μ - (2x))
julia> Symbolics.derivative(ℓ,logσ)
1 - (exp(-2logσ)*((x - μ)^2))\mu = \mathbb{E}_p[x] \approx 0.27
\sigma^2 = \mathbb{V}_p[x] \approx 0.03
Parameterized Measures

Ways of writing Normal(0,2)
-\log {\color{darkorange} \sigma} - \frac{1}{2}\left(\frac{x - \color{blue} \mu}{\color{darkorange} \sigma}\right)^2
Normal(0,2)
Normal(μ=0, σ=2)
Normal(σ=2)
Normal(mean=0, std=2)
Normal(mu=0, sigma=2)-\frac{1}{2} \left( \log {\color{darkorange} \sigma^2} - \frac{(x - {\color{blue} \mu})^2}{\color{darkorange} \sigma^2} \right)
Normal(μ=0, σ²=4)
Normal(mean=0, var=4)\frac{1}{2} \left( \log({\color{darkorange} τ}) - {\color{darkorange} τ} (x - {\color{blue} μ})^2 \right)
Normal(μ=0, τ=0.25)-{\color{darkorange} \log \sigma} - \frac{(x - {\color{blue} μ})^2}{2 e^{2 {\color{darkorange} \log \sigma}}}
Normal(μ=0, logσ=0.69)Computing Relative Log-Density

\text{Lebesgue}(\mathbb{R})
\text{Beta}(\alpha, \beta)
\frac{1}{\sqrt{2\pi}}\text{Lebesgue}(\mathbb{R})
\text{Normal}(\mu, \sigma^2)
\text{Lebesgue}(\mathbb{I})
+
—
+
—
IID Products


d = Beta(2,4) ^ (40,64)A PowerMeasure produces replicates a given measure over some shape.
⋆
⋆Independent and Identically Distributed
Products with Index Dependence


d = For(40,64) do i,j
Beta(i,j)
endFor(indices) do j
# maybe more computations
# ...
some_measure(j)
endFor produces independent samples with varying parameters.
Markov Chains


mc = Chain(Normal(μ=0.0)) do x Normal(μ=x) end
r = rand(mc)Define a new chain, take a sample
julia> take(r,100) == take(r,100)
trueThis returns a deterministic iterator
julia> logdensity(mc, take(r, 1000))
-517.0515965372Evaluate on any finite subsequence
Symbolic Evaluations

julia> using MeasureTheory, Symbolics
julia> @variables μ τ
2-element Vector{Num}:
μ
τ
julia> d = Normal(μ=μ, τ=τ) ^ 1000;
julia> x = randn(1000);
julia> ℓ = logdensity(d, x) |> expand
500.0log(τ) + 3.81μ*τ - (503.81τ) - (500.0τ*(μ^2))- Types and functions are generic, so symbolic manipulations work out of the box
- Compare
- MeasureTheory.jl
- Distributions.jl
julia> logdensity(Distributions.Normal(μ, 1 / √τ), 2.0)
ERROR: MethodError: no method matching logdensity(::Num, ::Float64)Working with Likelihoods

prior = HalfNormal()

\begin{aligned}
\color{#009cfa} \sigma &\color{#009cfa}\sim \text{Normal}_+(0,1) \\
\phantom{\color{#e47045} x_n} &\phantom{\color{#e47045} \sim \text{Normal}(0,\sigma}
\end{aligned}
Working with Likelihoods

prior = HalfNormal()
d = Normal(σ=2.0) ^ 10
lik = Likelihood(d, x)

\begin{aligned}
\color{#009cfa} \sigma &\color{#009cfa}\sim \text{Normal}_+(0,1) \\
\color{#e47045} x_n &\color{#e47045} \sim \text{Normal}(0,\sigma)
\end{aligned}
Working with Likelihoods

prior = HalfNormal()
d = Normal(σ=2.0) ^ 10
lik = Likelihood(d, x)
post = prior ⊙ lik
\begin{aligned}
\color{#009cfa} \sigma &\color{#009cfa}\sim \text{Normal}_+(0,1) \\
\color{#e47045} x_n &\color{#e47045} \sim \text{Normal}(0,\sigma)
\end{aligned}
{\color{#3ba64c} P(\sigma | x)} \propto {\color{#009cfa} P(\sigma)} {\color{#e47045} P(x | \sigma)}
Packages Using MeasureTheory.jl

- From Moritz Schauer
- Mitosis.jl
- MitosisStochasticDiffEq.jl
- ZigZagBoomerang.jl can use MeasureTheory for sparse posteriors
- From me
- In Soss.jl, every Model is also an AbstractMeasure
Funding


Thanks to PlantingSpace for funding for Spring 2021 https://planting.space
Thank You!
