What node is most important?

Casper van Elteren

Dynamic importance of nodes is poorly predicted by static topological features

arxiv.org/abs/1904.06654

Complex systems are ubiquitous

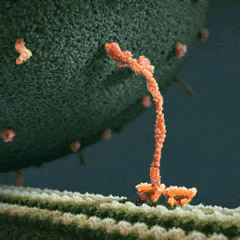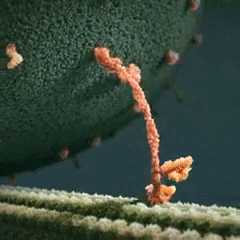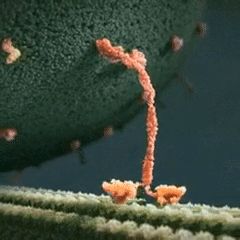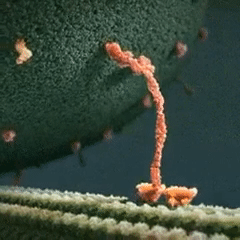
Structure
Dynamics
Emergent behavior

Most approaches are not applicable to complex systems:

Use simplified dynamics
Use structure as dynamic importance
Use overwhelming interventions

What is the most important node?

> What node drives the system?

\dot x_i = M_0(x_i) + \sum_i^N A_{ij} M_1(x_i) M_2(x_j)

Stationarity of system dynamics
Local linearity of state transitions
Memory-less dynamics
....

Wang et al. (2016)

However we have a many-to-one mapping

1. Simplified dynamics

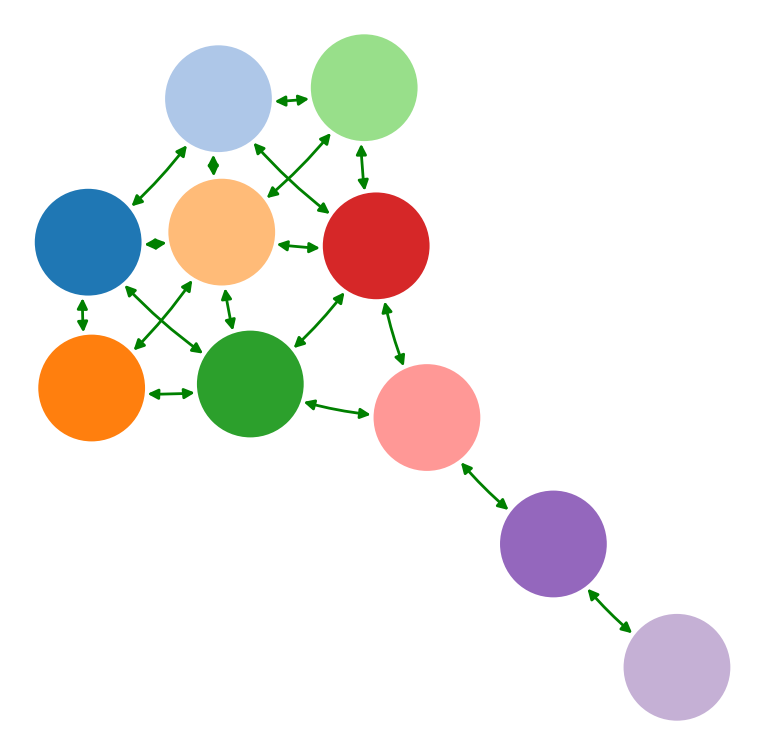
"Well-connected nodes are dynamically important"

2. Which feature to select?

N.B. implicit dynamics assumption!

Harush et al. (2017)

F_i \propto input \times output^{w-1}

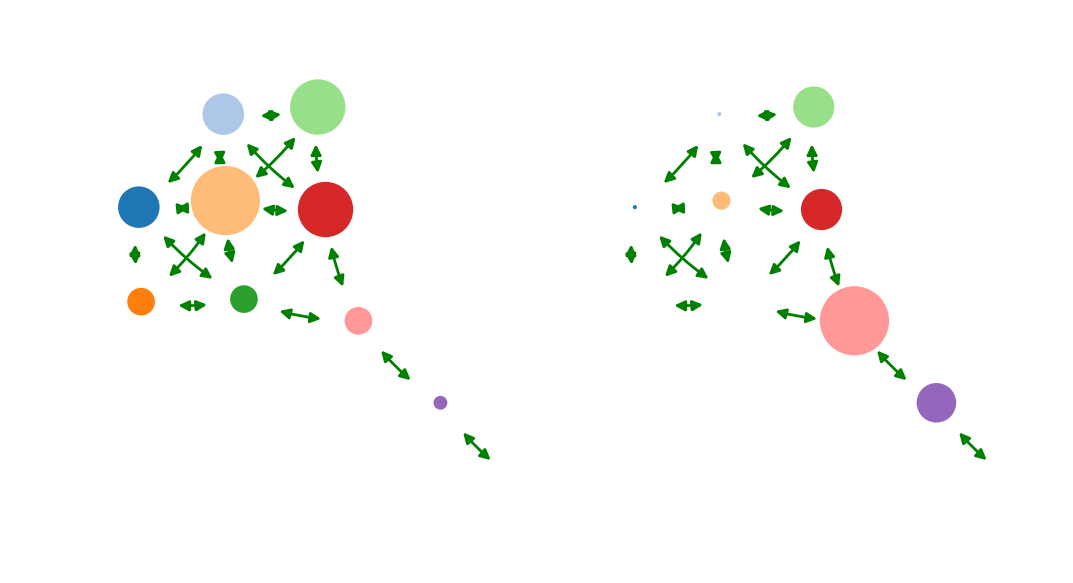
2. Dynamic importance interacts with structure

Genetic

Epidemic

Biochemical

Ecological

3. The size of intervention matters

Interventions are crucial for the scientific method
Many are overwhelming:
- Gene knockout
- Replacing signal

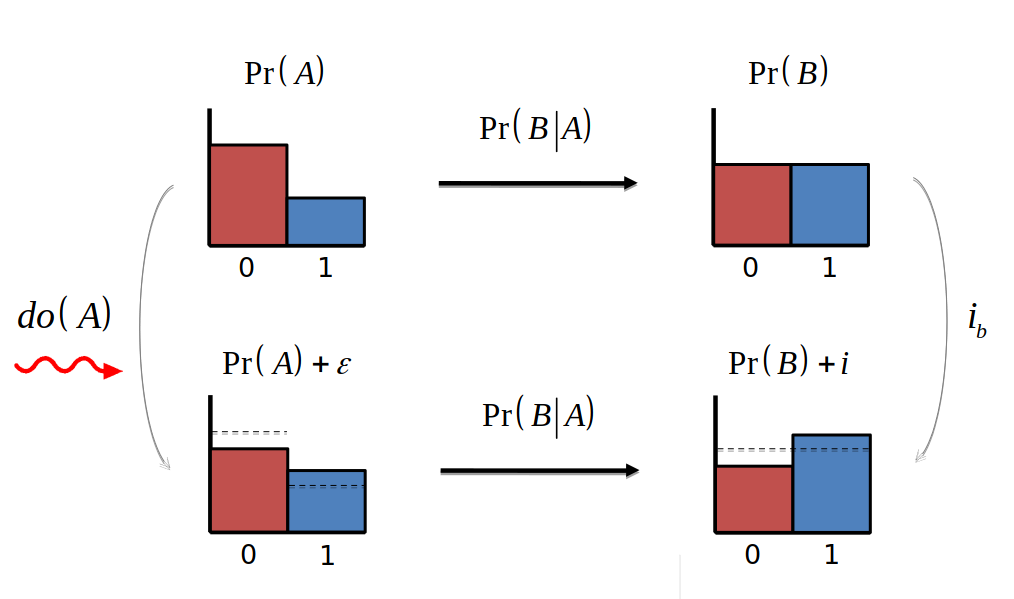
Pearl (2000)

Mechanism driving behavior are different under overwhelming interventions!

Summary

We have seen:

Most methods simplify the complex system
..use structure for identifying 'important' parts
..use overwhelming interventions

Possible solution: information theory

Information theory and complex systems

Traditional approaches are domain specific but all ask similar questions, e.g.:

What node is most important?
Does it exhibit criticality?
How robust is the system to removal of signals?
....

Quax et al. (2016)

How to achieve universal approach to study various complex behavior?

There is a need for a universal language that decouples syntax from semantics

Quax et al. (2016)

Domain specific

\dot x_i = M_0(x_i) + \sum_i^N A_{ij} M_1(x_i) M_2(x_j)

S = \{s_1, s_2, \dots, s_n\}

Quantify in terms of "information"

I(s_i : S)

Traditional approach

Information viewpoint

Down

...

P(System)

Down

...

P(Bird)

Shannon (1948)

Information Entropy: "Amount of uncertainty"

Mutual information: "Shared information"

H(X) = - \sum_{x \in X} P(x) \log P(x)

\begin{aligned} I(X : Y) &= \sum_{x \in X y \in Y} P(x, y) \log \frac{P(x,y)}{P(x)P(y)}\\ &= H(X) - H(X | Y)\\ &= H(Y) - H(Y | X)\\ \end{aligned}

N.B. No assumption on what generates P

H(X) = - \frac{1}{2} \log \frac{1}{2} - \frac{1}{2} \log \frac{1}{2} = 1

\begin{aligned} P(Heads) = \frac{1}{2} \\ P(Tails) = \frac{1}{2} \\ \end{aligned}

H(X) = 0

\begin{aligned} P(Heads) = 0 \\ P(Tails) = 1 \\ \end{aligned}

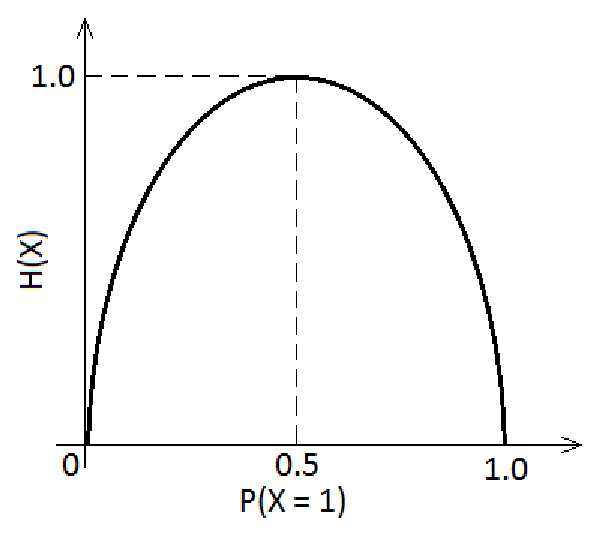
Information in complex systems

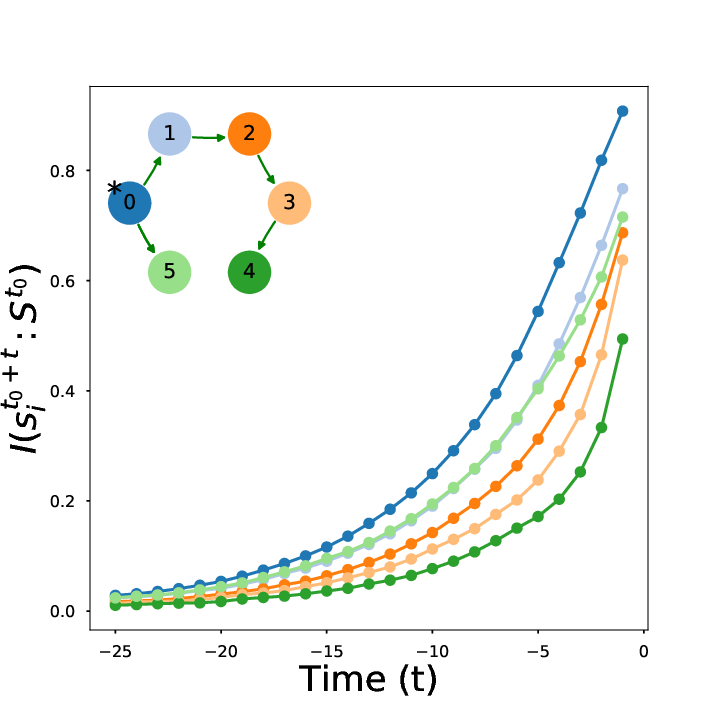
Given ergodic system S

Information will always decrease as function of time

Driver-node will share the most information with the system over time

Diminishing role of hubs

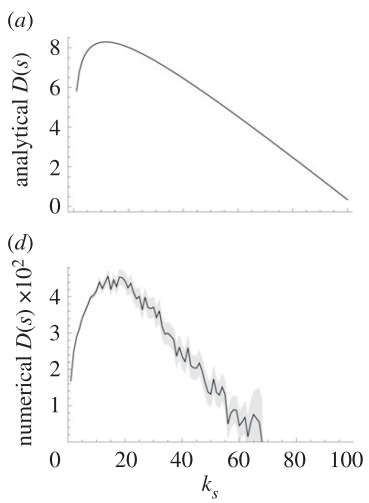
Quax & Sloot (2013)

Infinitely sized networks
Locally tree-like
No-self loops

Degree

Numerical

Analytical

d(s_i) = \{t : I(s_i^{t_0 + t} : S^{t_0}) = \frac{1}{2} H(s_i) \}

Goals

Answer:

Can information theory tools be used on real-world systems?
Does well-connectedness translate to dynamical importance in real-world systems?
Does intervention size matter in real-world systems?

Prior results:

Assume dynamics
Dynamics interact with structure
Overwhelming interventions
Theoretical

Goal: identify driver-node in real-world systems

Application domain

Mildly depressed patients
- Center for epidemiologic studies depression scale (CES-D)
- Changing lives for older couples (CLOC), N = 241

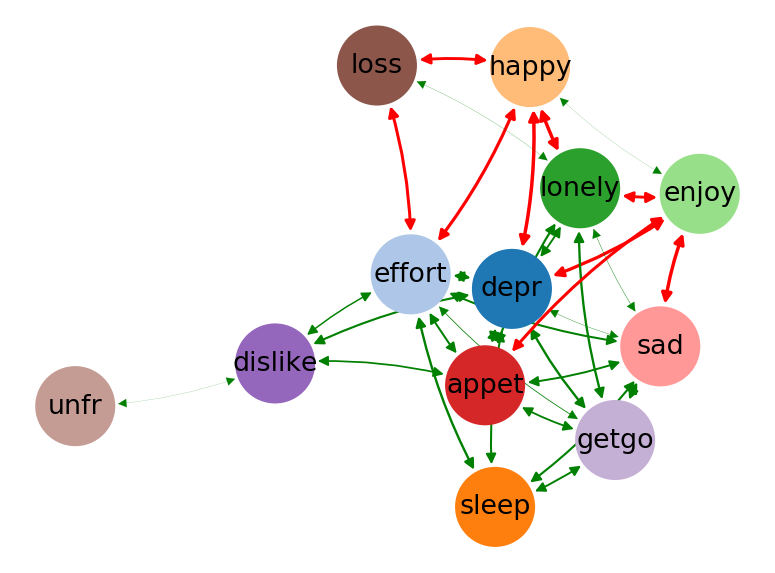
Fried et al. (2015)

Node dynamics

P(s_i ^ t | L_i ^ {t-1}) \propto \exp( -\frac{E(x)}{T})

Ising spin dynamics

s_i \in \{-1, 1\}

Glauber (1963)

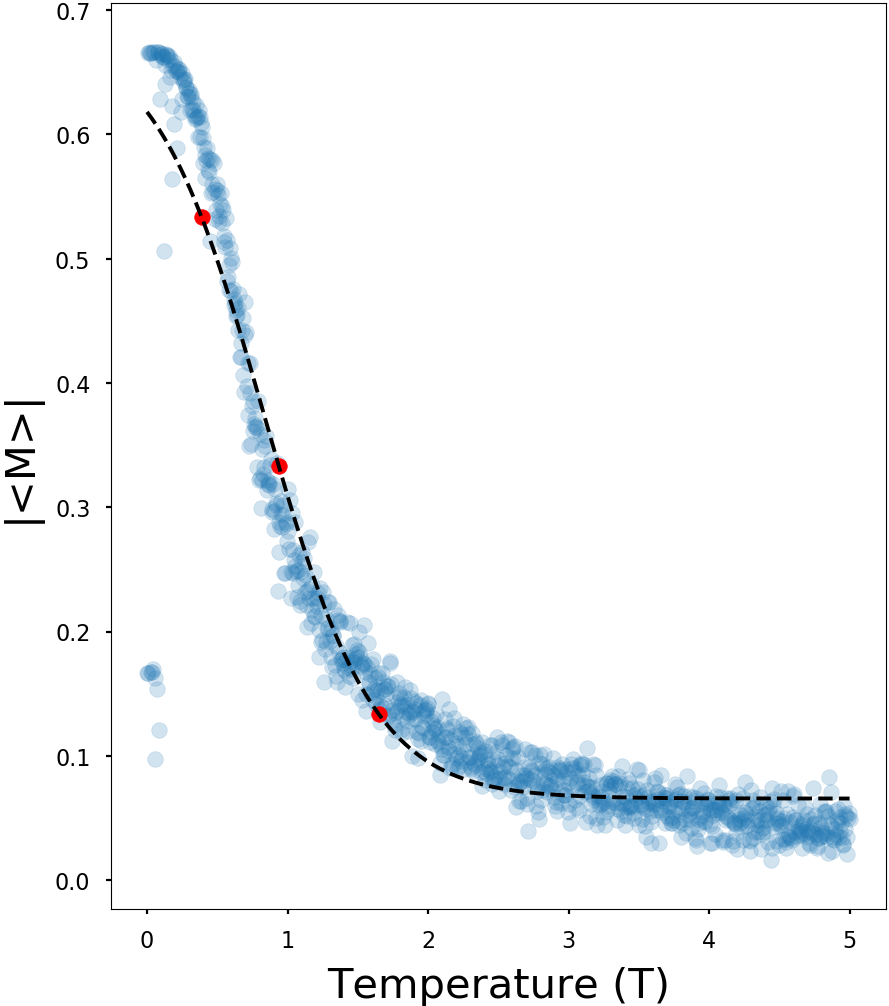
Used to model variety of behavior

Neural dynamics
Voting behavior
....

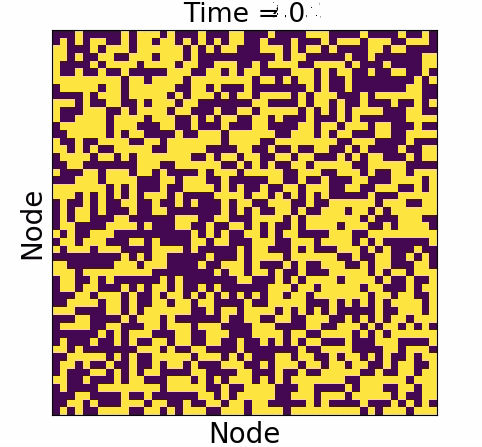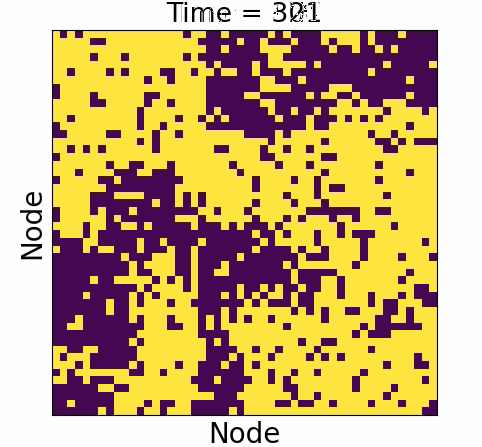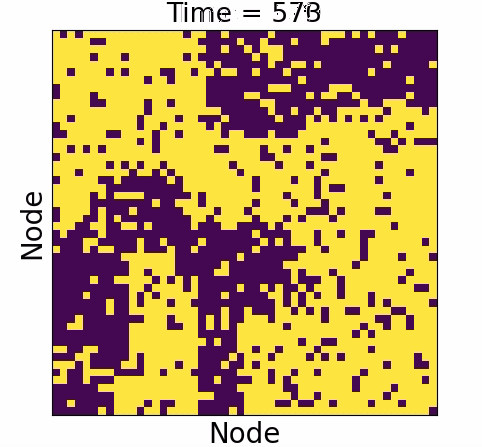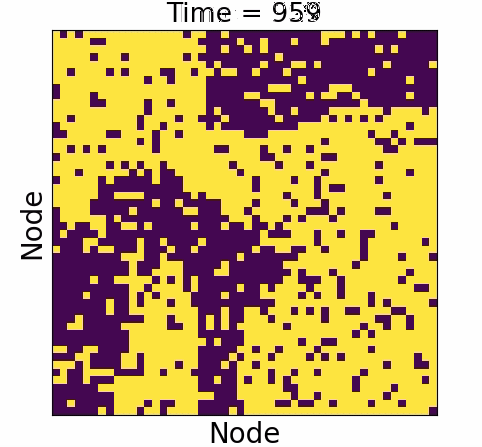
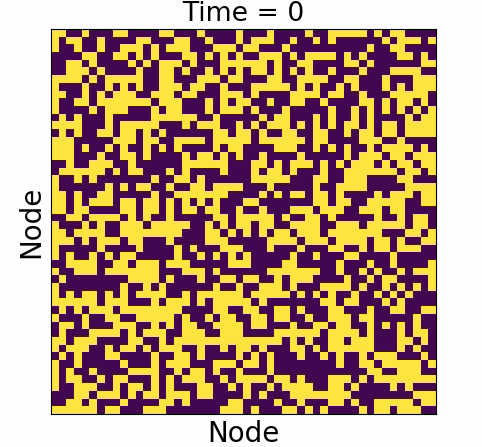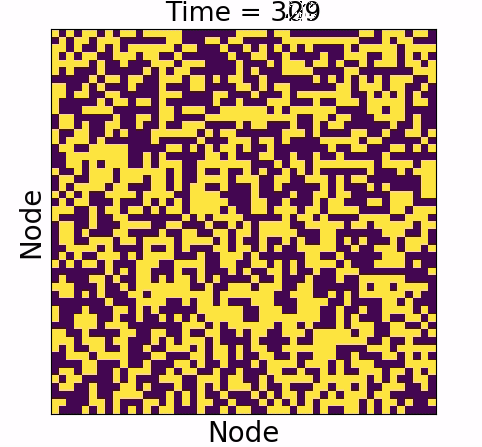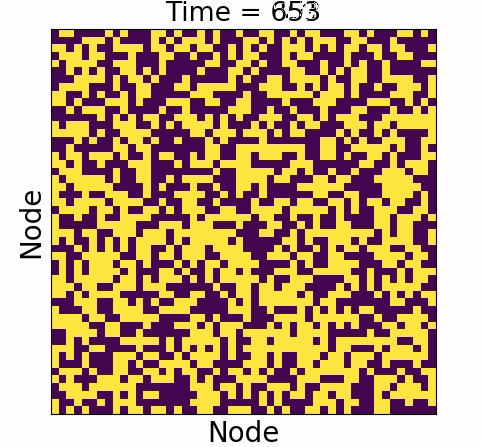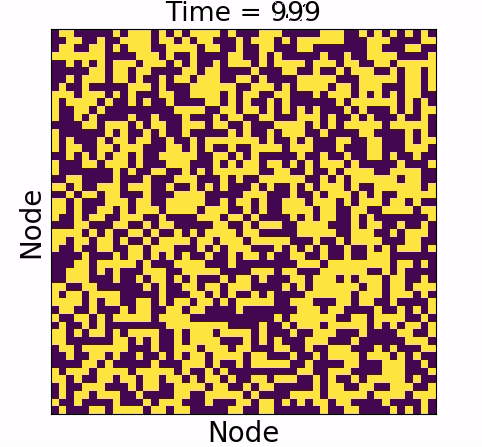
Causal influence

Causal influence forms the ground truth

Underwhelming :
Overwhelming:

E = 0.1

E = \infty

Causal impact

\gamma_i := \sum_{t=0}^\infty \sum_{j}^N D(P_i(s_j)' || P_i(s_j)) \Delta t

Advantages of KullBack-Leibler divergence:

Non Negative
Zero iff P' == P
No assumption on P
Optimality in coding setting
- Embodies extra bits needed to code samples from P' given code P

Information impact

Node with largest causal influence has highest information impact
Observations only!
- No perturbations required

\mu_i := \sum_{t=0}^\infty I(s_i^{t_0 + t} : S^{t_0}) \Delta t

Structural metrics

Name	What does it measure?
Betweenness	Shortest path
Degree	Local influence
Current flow	Least resistance
Eigenvector	Infinite walks

Statistical procedure

Ind. var max(x)	Dep. var
- Degree centrality - Betweenness centrality - Current flow centrality - Eigenvector centrality - Information impact	Causal impact - Underwhelming - Overwhelming

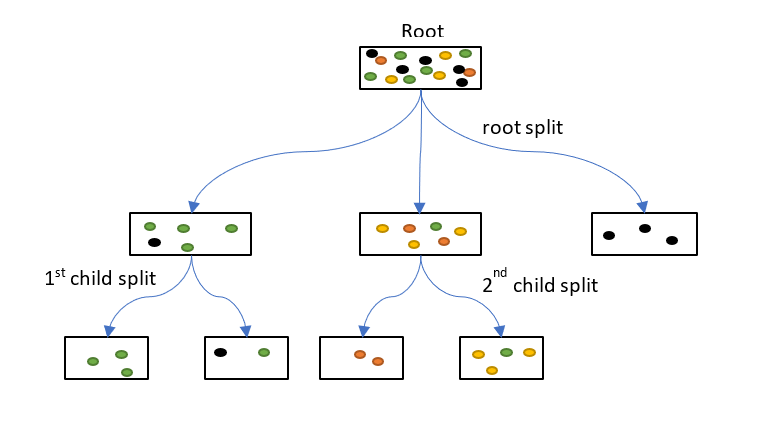
Classification with random forest:

Random forest classifier

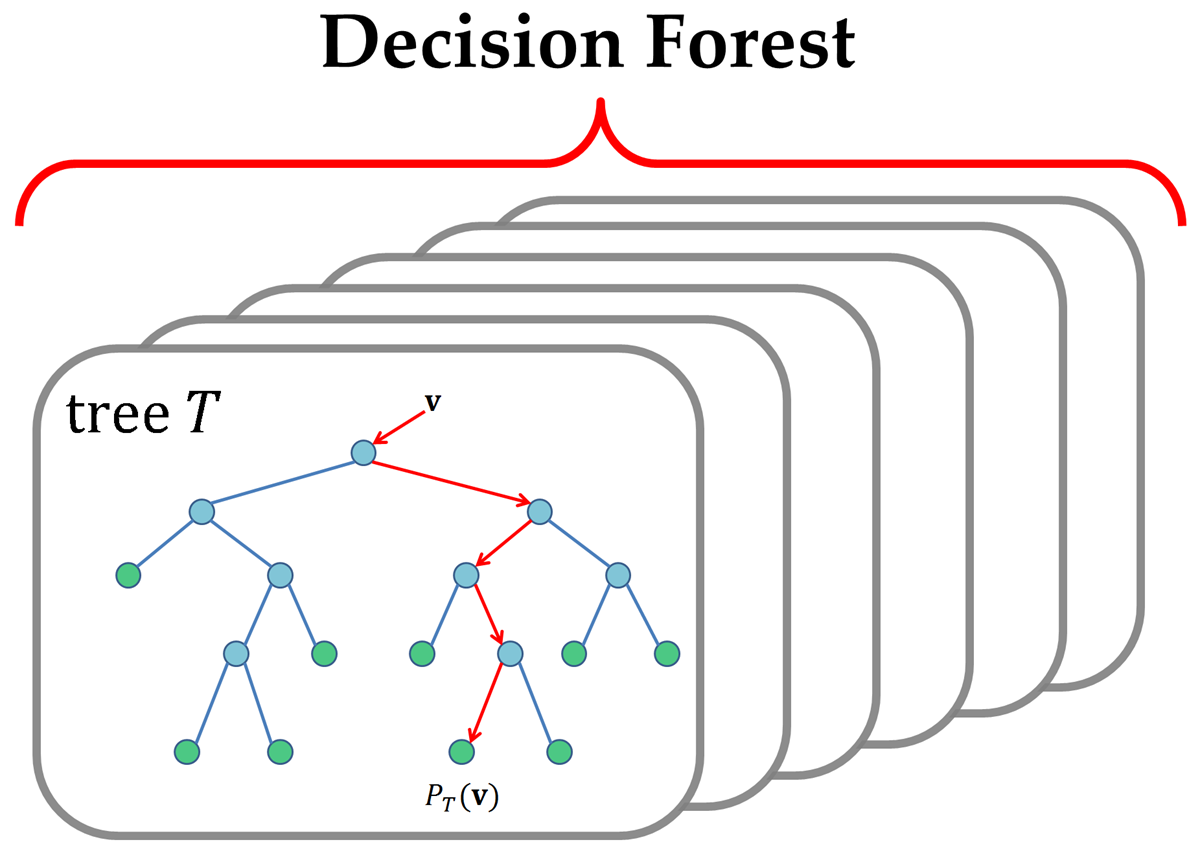
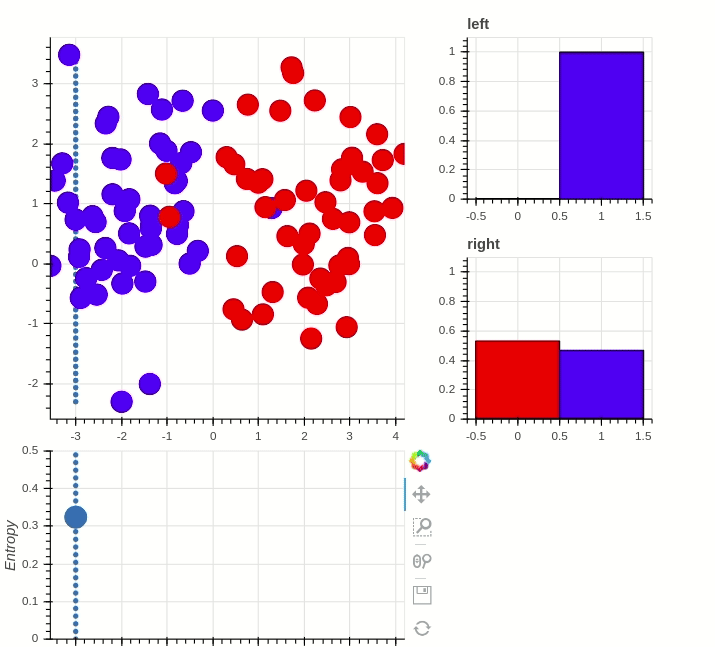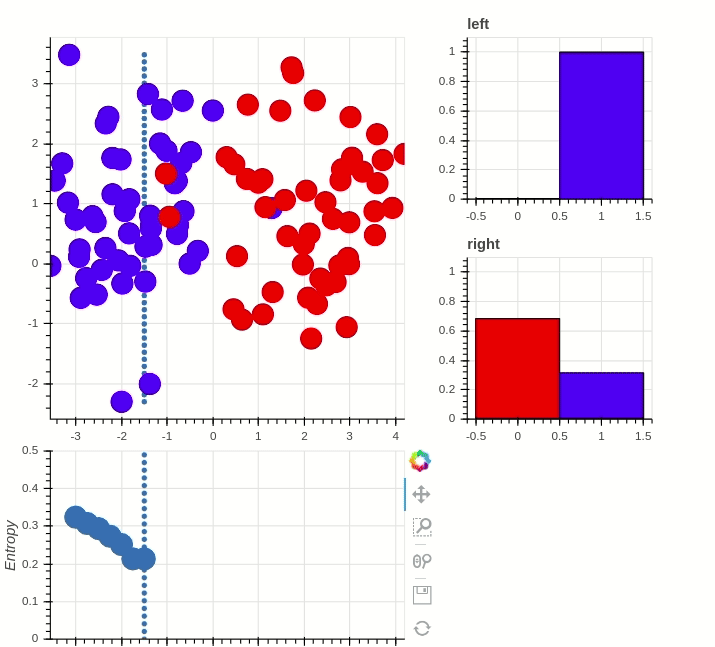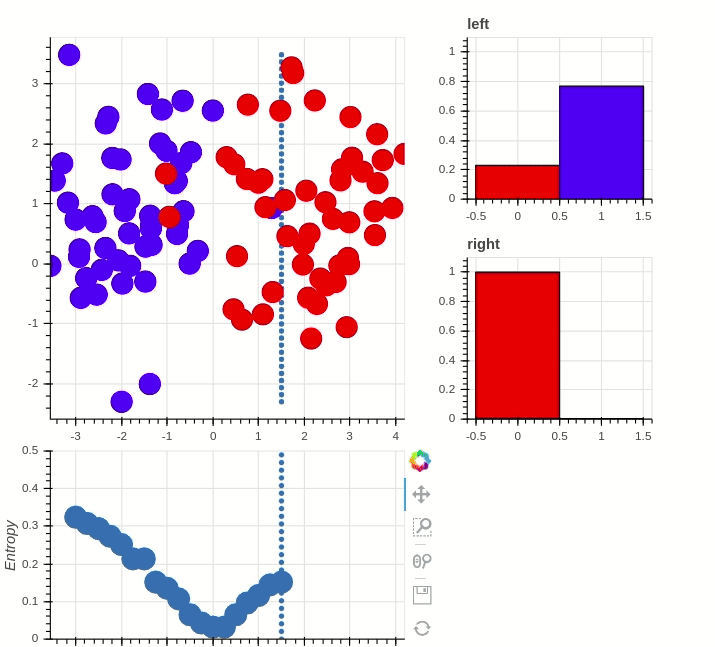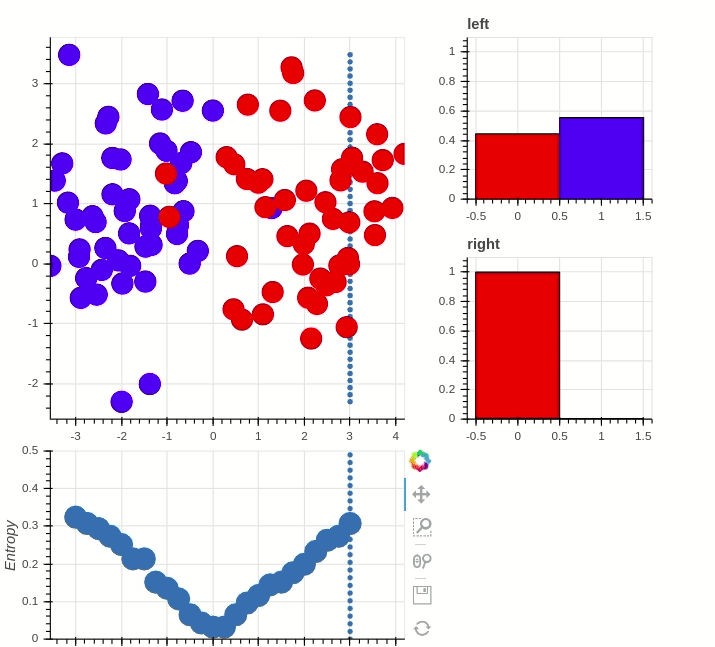
RNF classifier with high prediction accuracy

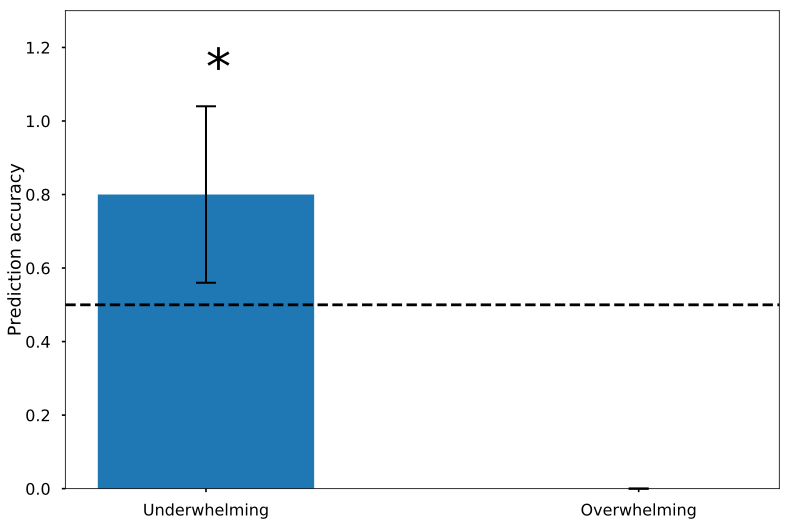
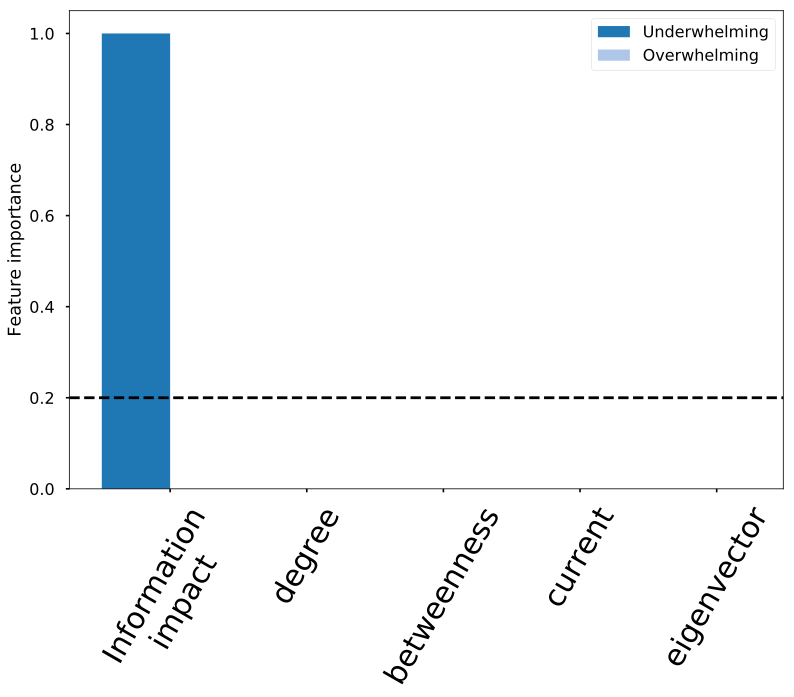
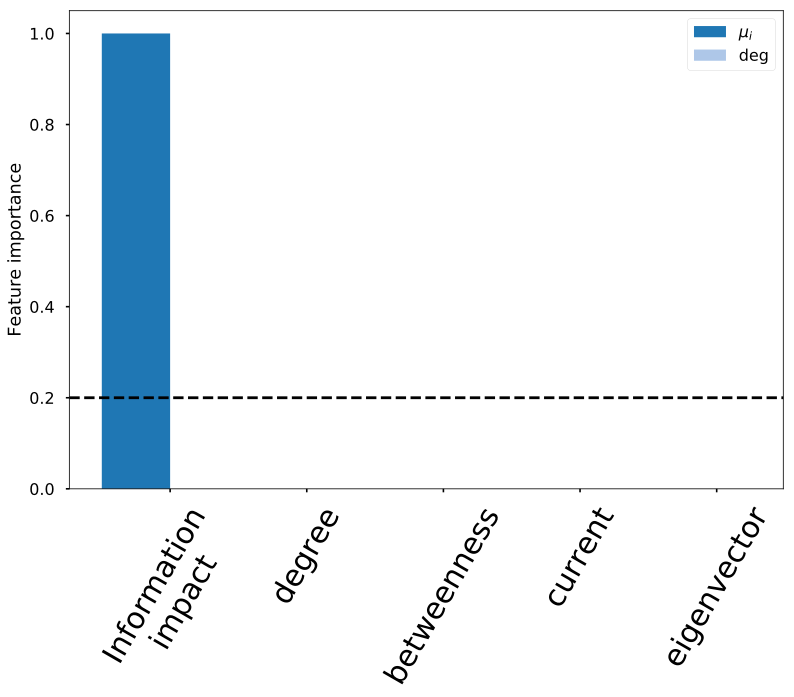
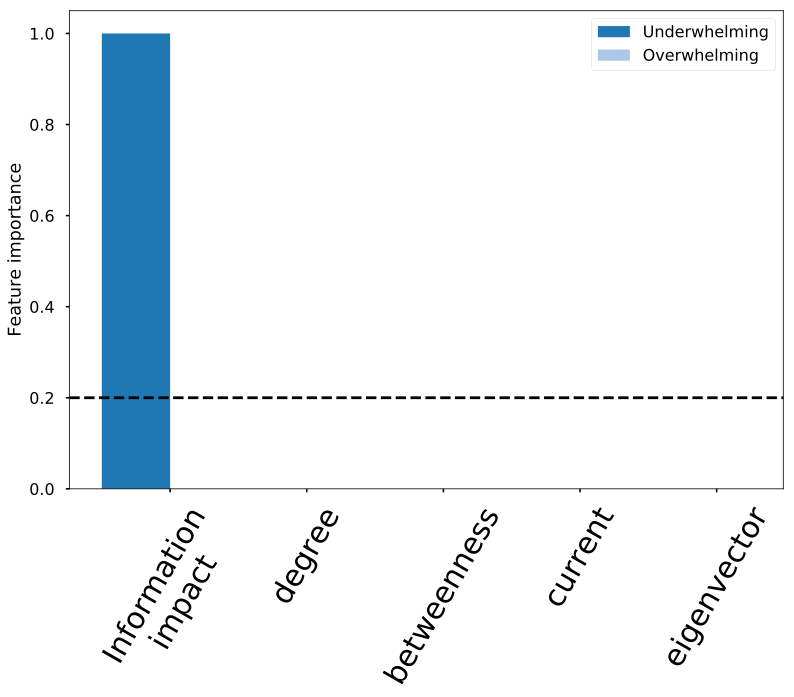
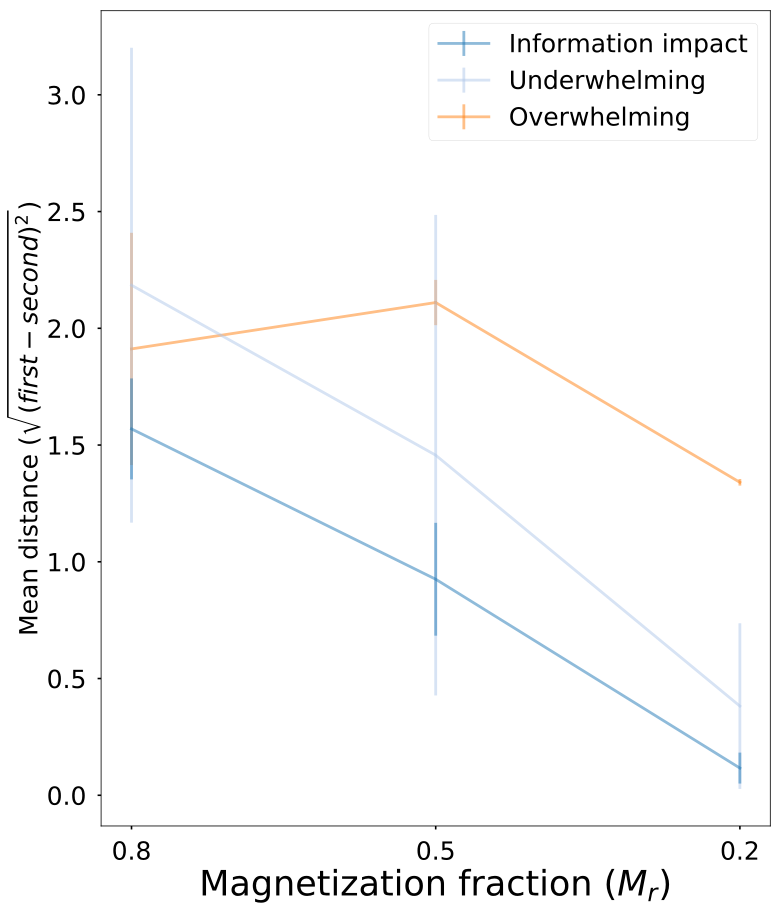
Underwhelming does not match overwhelming causal impact
Information impact matches underwhelming causal impact

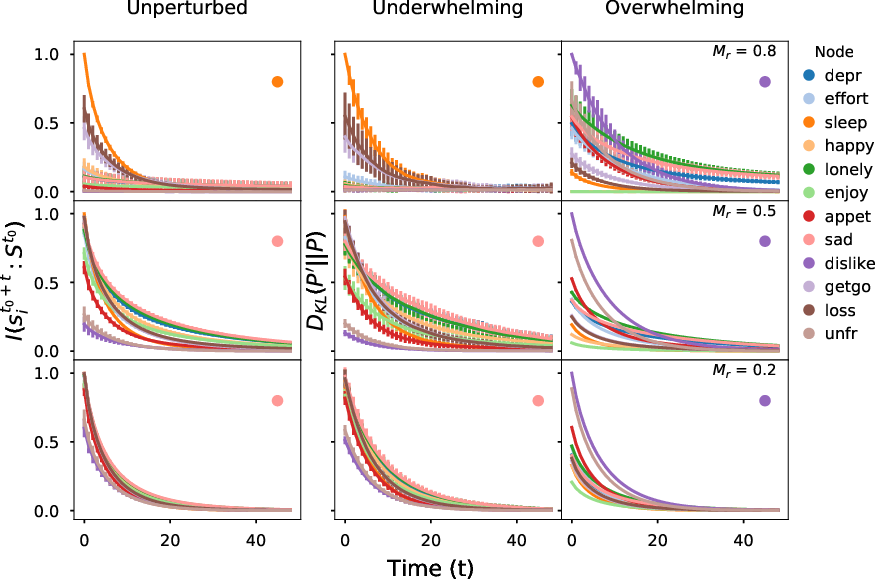
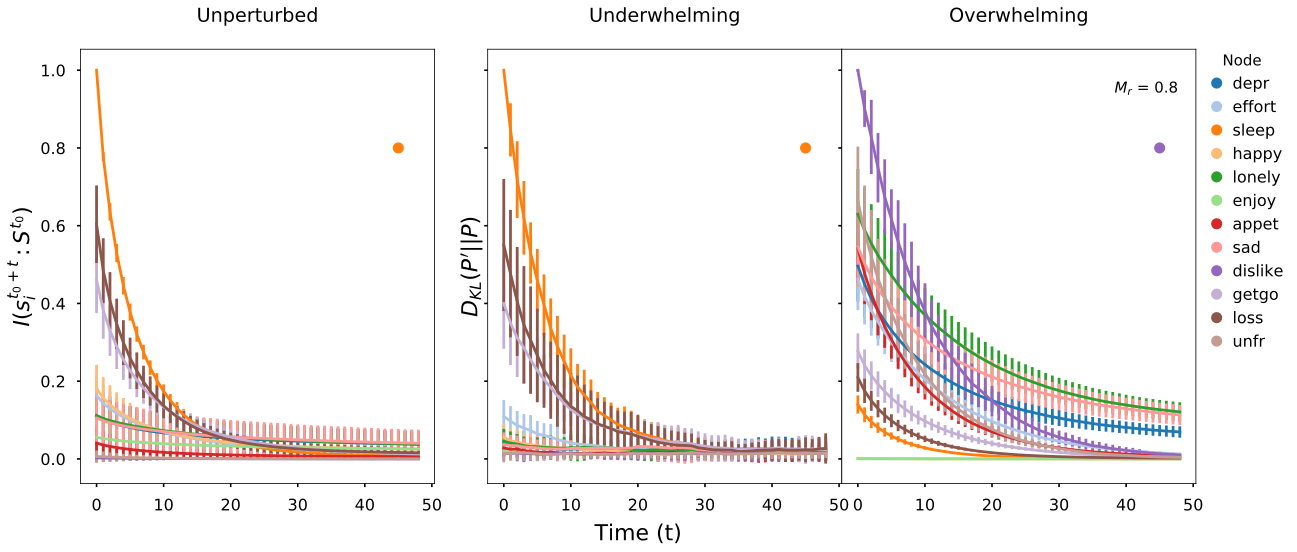
Information impact captures driver-node change

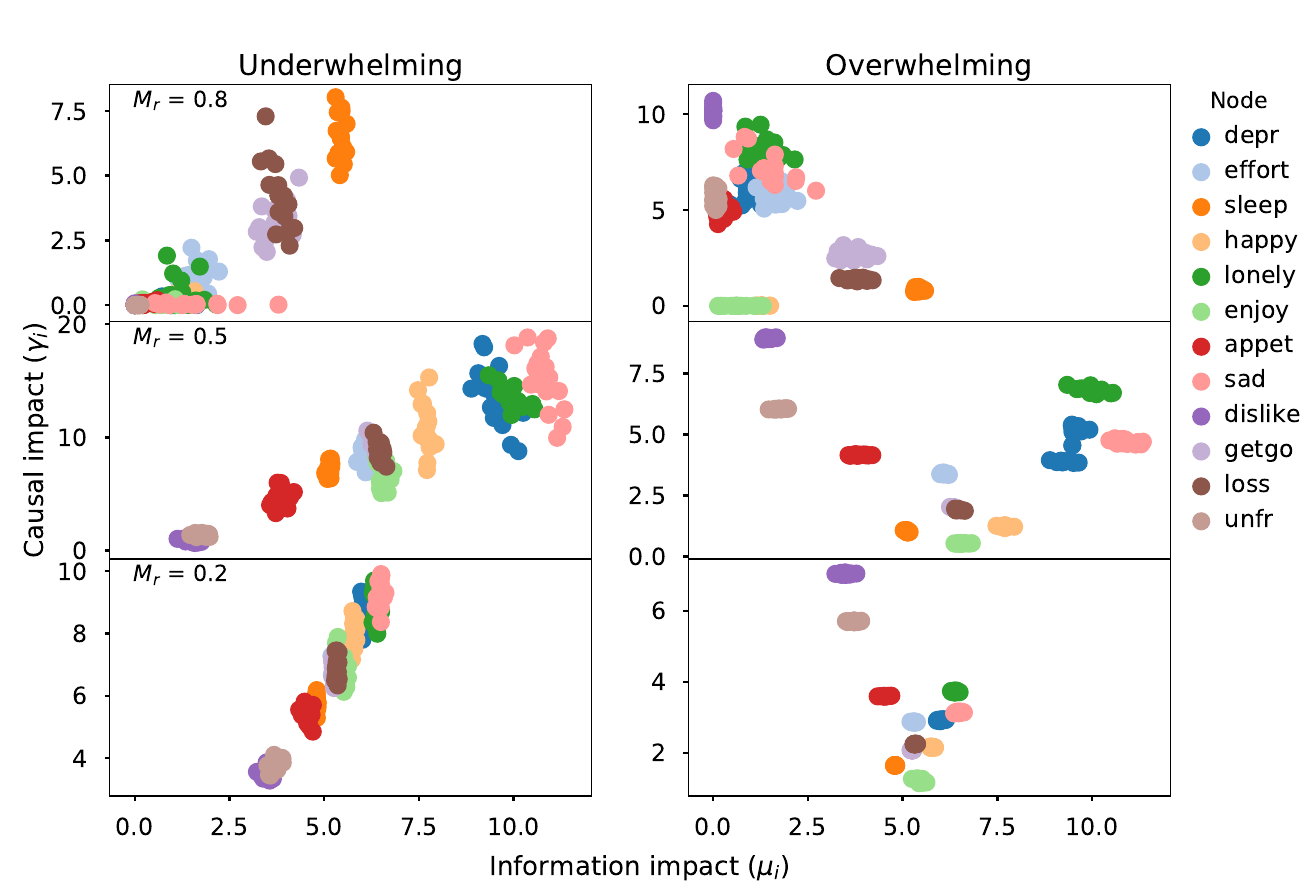
Information impact varies linearly with low causal impact

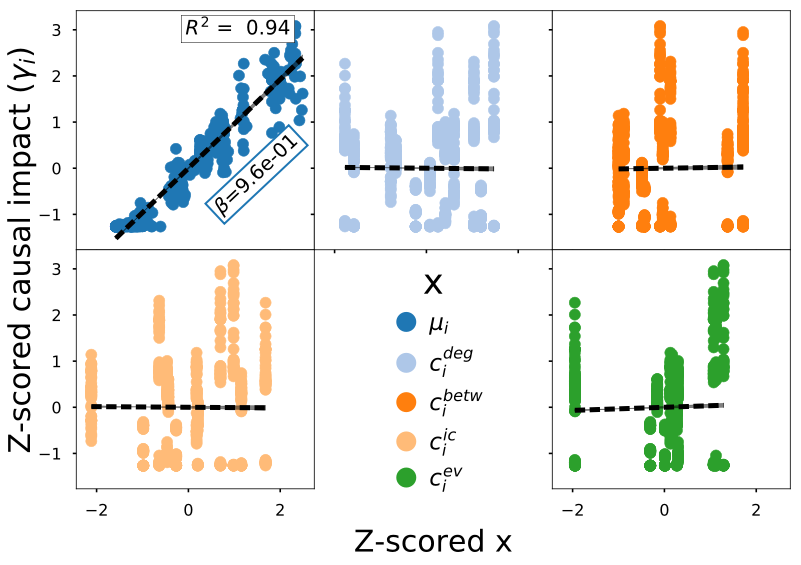
No structural metric showed a linear relation with low causal impact
Information impact was highly linear with low causal impact

Summary

Information impact predict driver-node for unperturbed dynamics
Intervention size matters
Structural metrics don't identify driver-node well

Take-home message:

Structural connectedness != dynamic importance

Future direction

Does information impact generalize well to other graphs?
Does it generalize well to other dynamics?
Can it be used to detect transient structures?
Asymmetry in time effects
....

Acknowledgement

A big thanks to dr. Rick Quax for his supervision

Models

Information

toolbox

Plotting toolbox

IO toolbox

cvanelteren.github.io

- Fast

- Extendable

- User-friendly

Information toolbox

Reference

Glauber, R. J. Time-dependent statistics of the Ising model. Journal of Mathematical Physics 4, 294–307 (1963).
Quax, R., Apolloni, A. & Sloot, P. M. a. The di-
minishing role of hubs in dynamical processes
on complex networks. Journal of the Royal Soci-
ety, Interface / the Royal Society 10, 20130568. arXiv:
1111.5483 (2013).
Quax, R., Har-Shemesh, O., Thurner, S., & Sloot, P. (2016). Stripping syntax from complexity: An information-theoretical perspective on complex systems. arXiv preprint arXiv:1603.03552.
Harush, U. & Barzel, B. Dynamic patterns of in-
formation flow in complex networks. Nature Com-
munications 8, 1–11 (2017).
Harush, U. & Barzel, B. Dynamic patterns of in-
formation flow in complex networks. Nature Com-
munications 8, 1–11 (2017).
Fried, E. I. et al. From loss to loneliness: The re-
lationship between bereavement and depressive
symptoms. Journal of Abnormal Psychology 124, 256–
265 (2015).

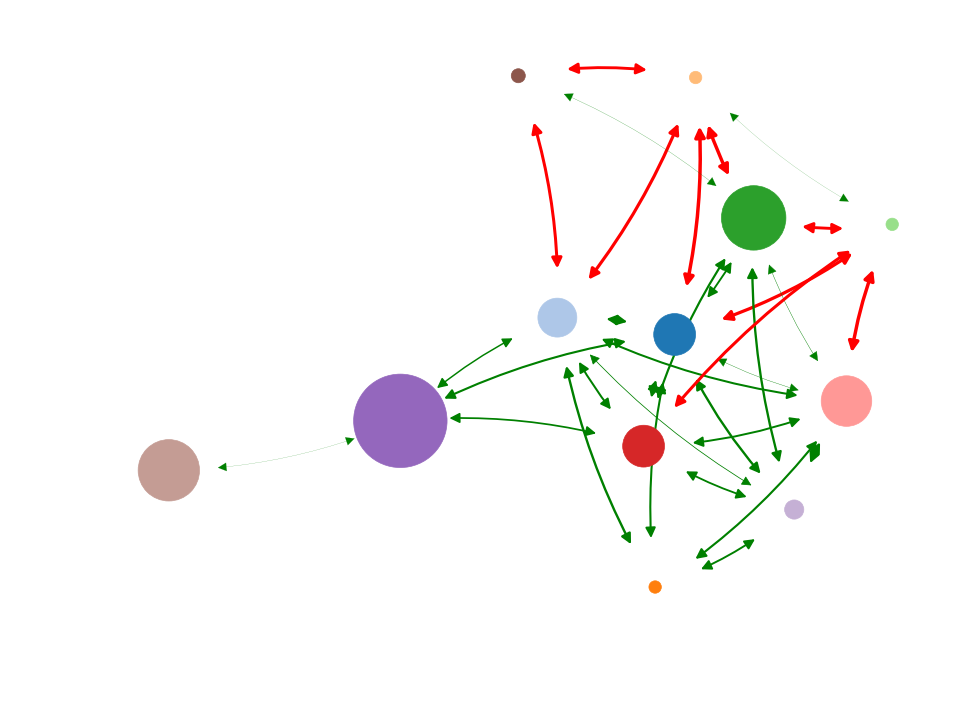
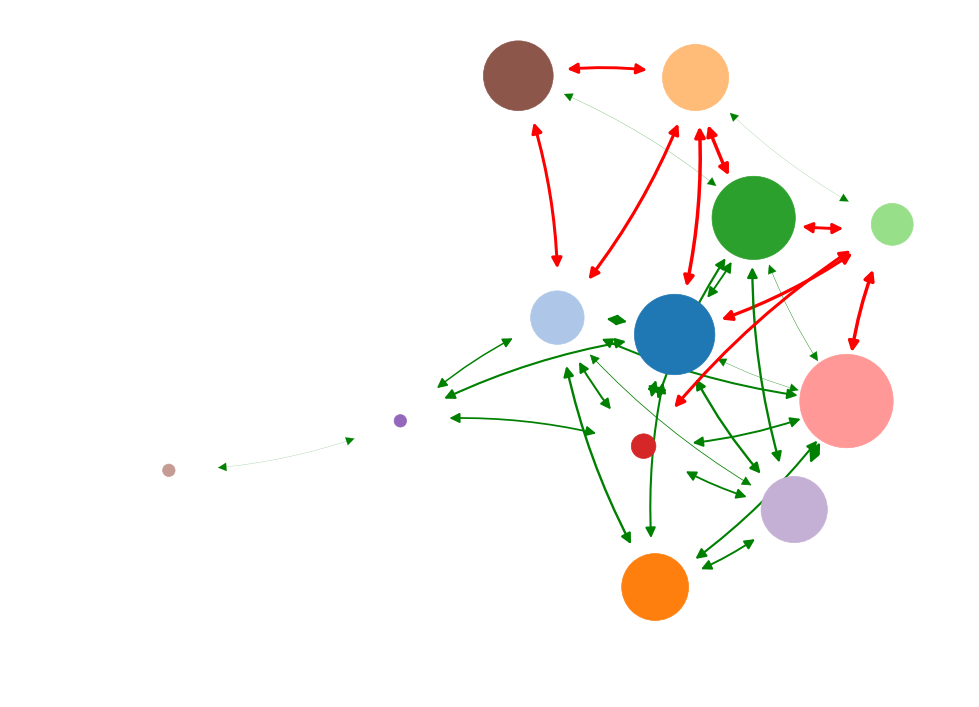
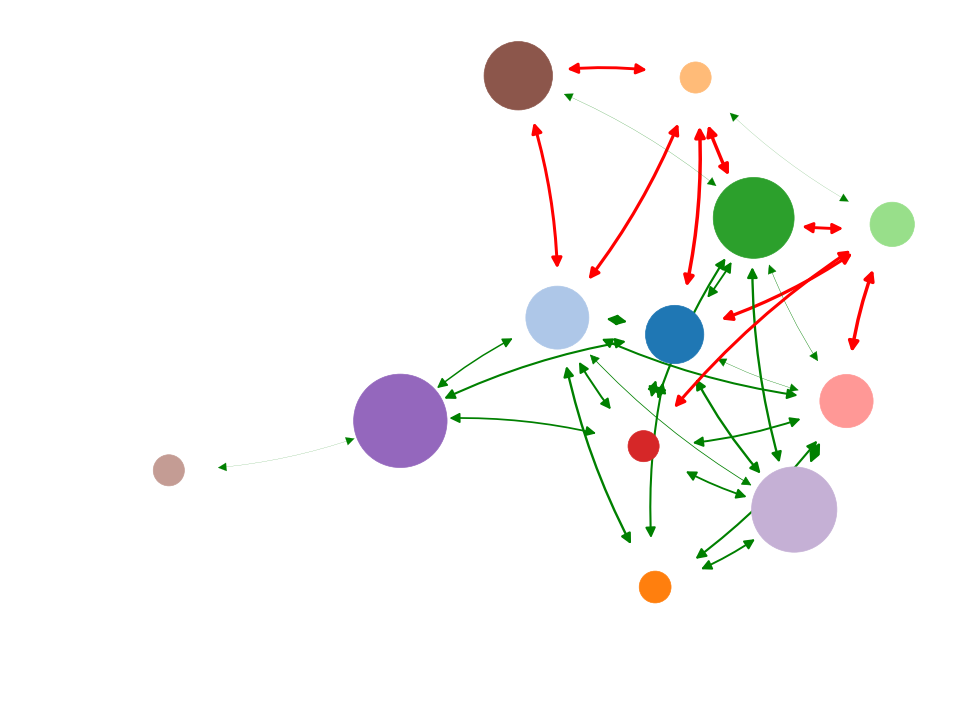
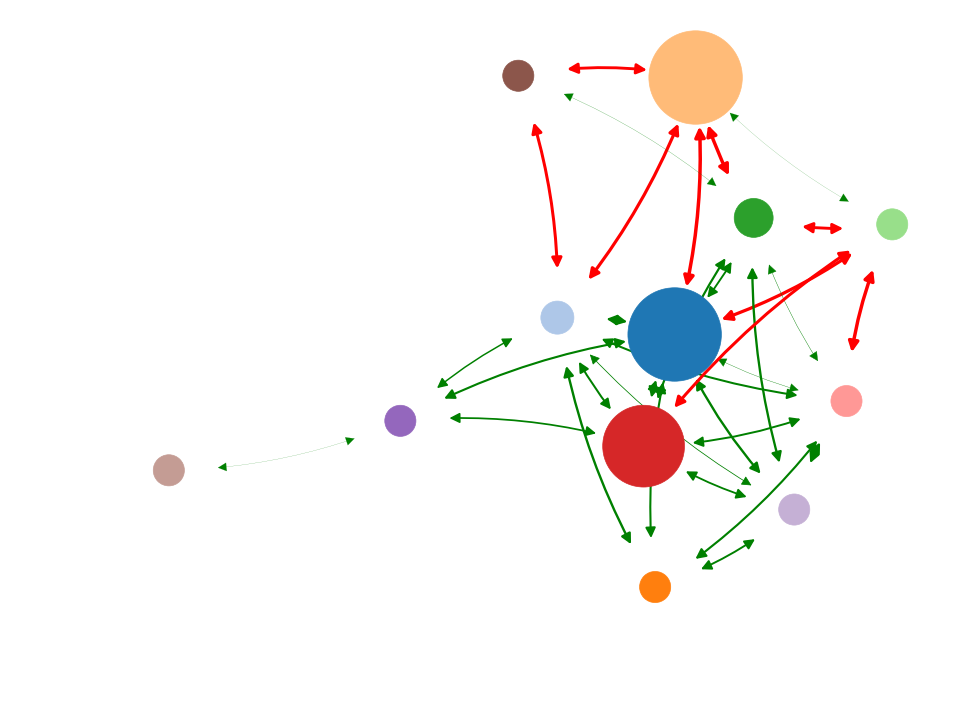
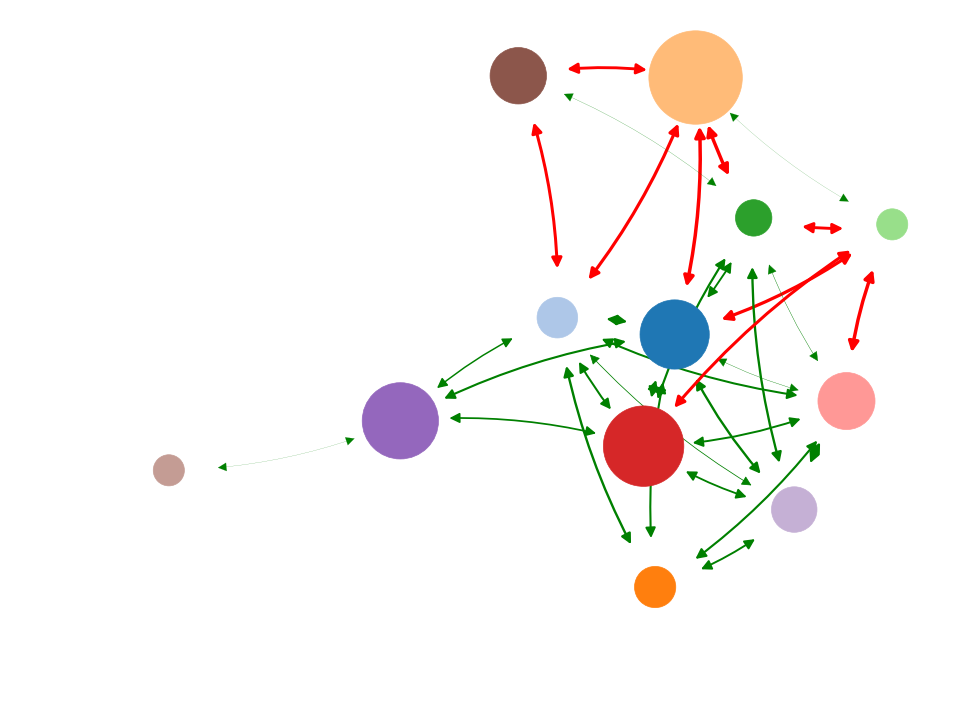
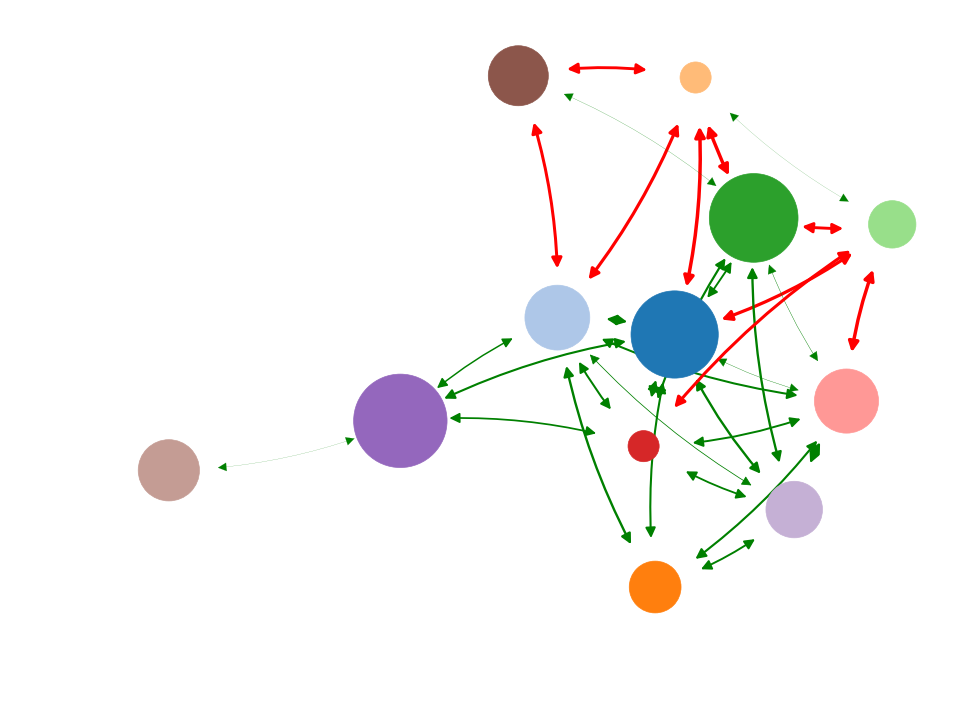
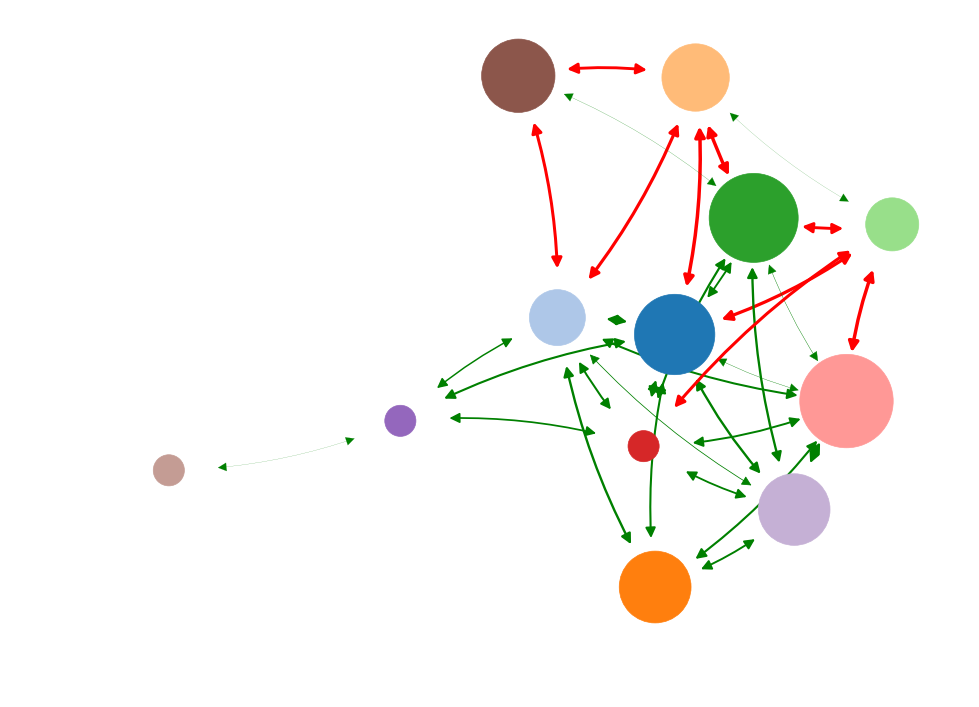
Information impact

Betweenness

Degree

Current flow

Eigenvector

Low causal impact

High causal impact

Shannon (1948)

P(A)

P(B | A = a)

I(A : A)

I(A : B)

Entropy

Mutual information

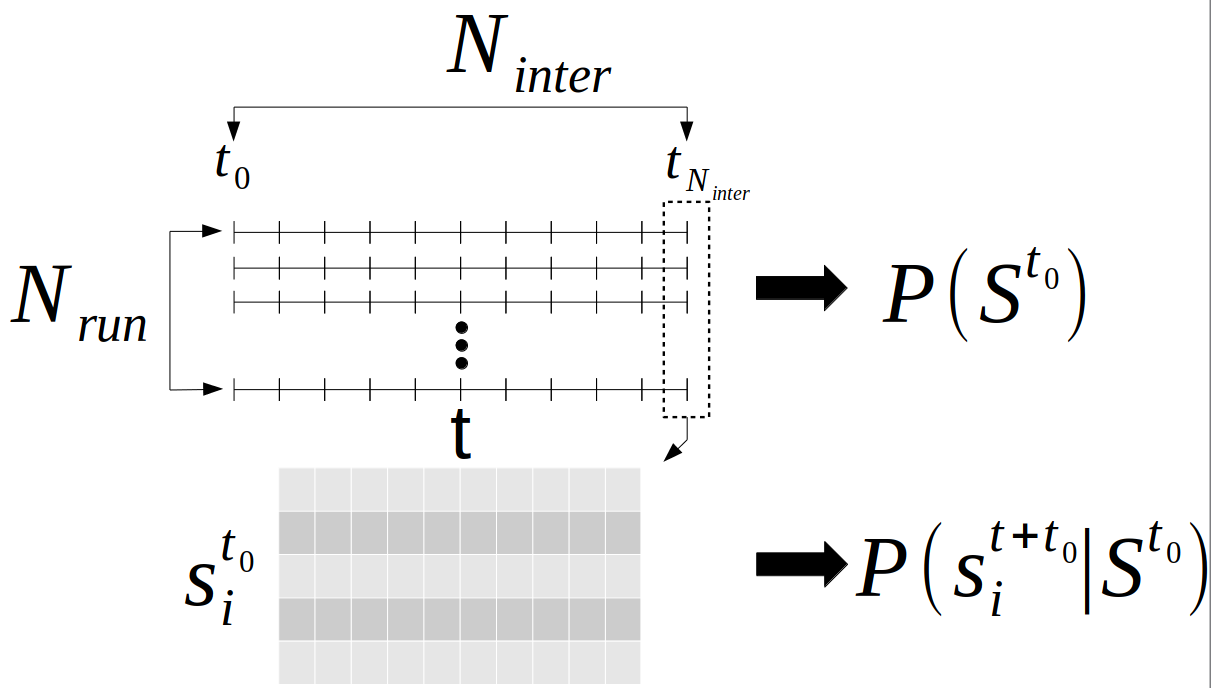
Numerical methods

Monte-Carlo methods
Compare information impact and centrality metrics
Intervention:
- Underwhelming
- Overwhelming

P(S^{t_0})

P(s_i^{t_0 + t} | S^{t_0})

E = 0.1

E = \infty

github.com/cvanelteren

Statistical procedure

Quantify accuracy with random forest classifier
Validation with Leave-One-Out cross-validation

\begin{aligned} D &= \{(X_1, Y_1), \dots, (X_N, Y_N)\}\\ Y_{n \in N} &= \{y_{m1}, \dots, y_{mN}\}\\ X_{n \in N} &= \{x_{m1}, \dots, k_{mN} \}\\ \end{aligned}

m = amount of regressors

N = number of samples