Generado laberintos utilizando el algoritmo de Prim
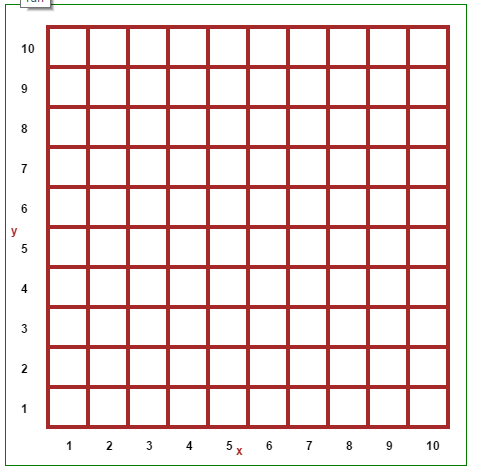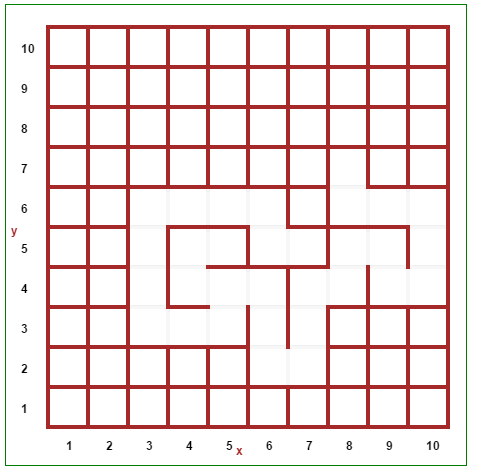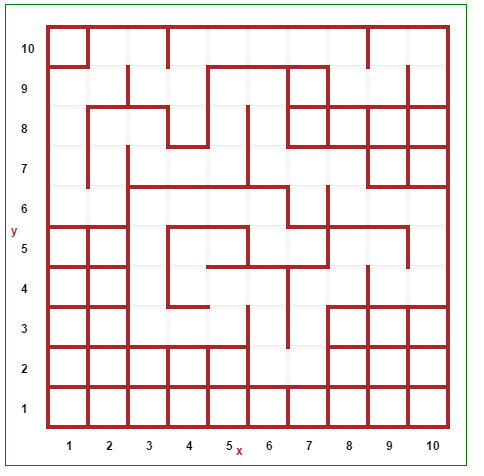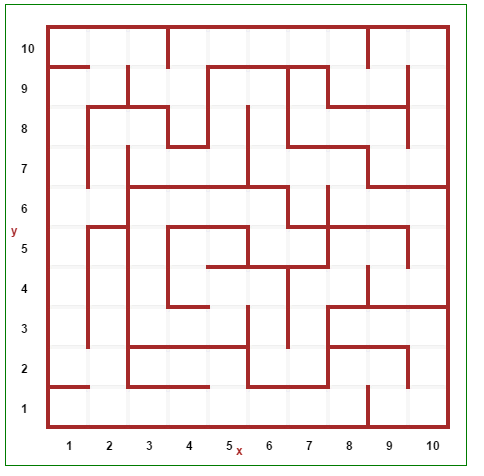
Algoritmo
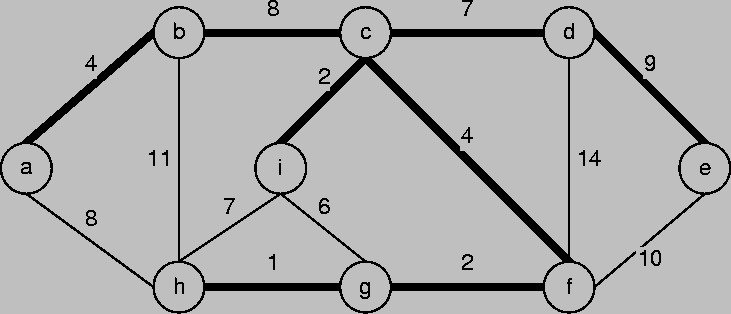
- Se elige un vertice arbitratio de G (el grafo), y se agrega a un conjunto V, inicialmente vacío.
- Se elige el arco con el peso mínimo de G, que conecte un vértice en V con otro vértice que no pertenezca a V.
- Se agrega el arco al mínimo arbol de expanción y el segundo vértice a V.
- Se repite el paso 2 y 3 hasta que V incluya todos los vértices en G.
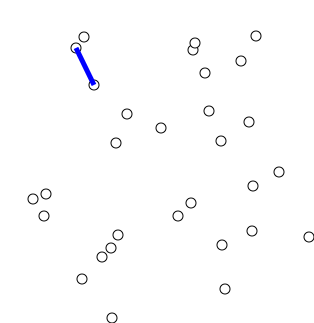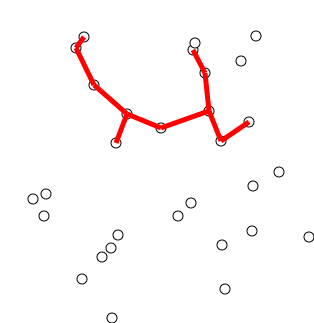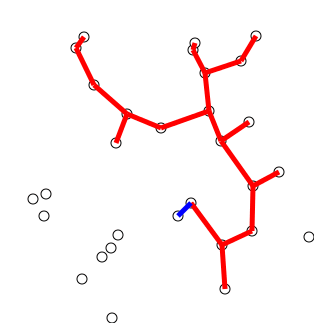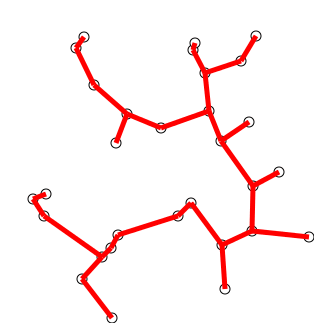
Complejidad temporal
Búsqueda en matriz de adjacencia :
O(V^2)
O(V2)
Pila binaria y lista de adyacencia :
O(Vlog(V) + Elog(V))
O(Vlog(V)+Elog(V))
Adaptando el algoritmo
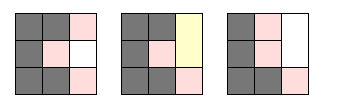
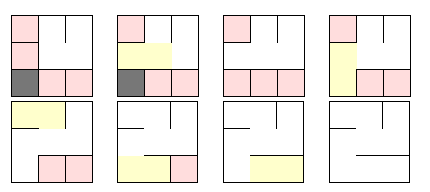
Solo cambiar el paso 2, entonces en vez de seleccionar el arco con el menor peso, se selecciona uno aleatorio, evitando seleccionar la "frontera" del laberinto.



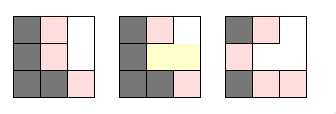
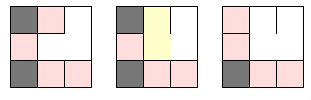
# --------------------------------------------------------------------
# 1. Allow the maze to be customized via command-line parameters
# --------------------------------------------------------------------
width = (ARGV[0] || 10).to_i
height = (ARGV[1] || width).to_i
seed = (ARGV[2] || rand(0xFFFF_FFFF)).to_i
srand(seed)
# --------------------------------------------------------------------
# 2. Set up constants to aid with describing the passage directions
# --------------------------------------------------------------------
N, S, E, W = 1, 2, 4, 8
IN = 0x10
FRONTIER = 0x20
OPPOSITE = { E => W, W => E, N => S, S => N }
# --------------------------------------------------------------------
# 3. Data structures and methods to assist the algorithm
# --------------------------------------------------------------------
grid = Array.new(height) { Array.new(width, 0) }
frontier = []
def add_frontier(x, y, grid, frontier)
if x >= 0 && y >= 0 && y < grid.length && x < grid[y].length && grid[y][x] == 0
grid[y][x] |= FRONTIER
frontier << [x,y]
end
end
def mark(x, y, grid, frontier)
grid[y][x] |= IN
add_frontier(x-1, y, grid, frontier)
add_frontier(x+1, y, grid, frontier)
add_frontier(x, y-1, grid, frontier)
add_frontier(x, y+1, grid, frontier)
end
def neighbors(x, y, grid)
n = []
n << [x-1, y] if x > 0 && grid[y][x-1] & IN != 0
n << [x+1, y] if x+1 < grid[y].length && grid[y][x+1] & IN != 0
n << [x, y-1] if y > 0 && grid[y-1][x] & IN != 0
n << [x, y+1] if y+1 < grid.length && grid[y+1][x] & IN != 0
n
end
def direction(fx, fy, tx, ty)
return E if fx < tx
return W if fx > tx
return S if fy < ty
return N if fy > ty
end
# --------------------------------------------------------------------
# 4. Routines for displaying the maze
# --------------------------------------------------------------------
def empty?(cell)
cell == 0 || cell == FRONTIER
end
def display_maze(grid)
print "\e[H" # move to upper-left
puts " " + "_" * (grid[0].length * 2 - 1)
grid.each_with_index do |row, y|
print "|"
row.each_with_index do |cell, x|
print "\e[41m" if cell == FRONTIER
if empty?(cell) && y+1 < grid.length && empty?(grid[y+1][x])
print " "
else
print((cell & S != 0) ? " " : "_")
end
print "\e[m" if cell == FRONTIER
if empty?(cell) && x+1 < row.length && empty?(row[x+1])
print((y+1 < grid.length && (empty?(grid[y+1][x]) || empty?(grid[y+1][x+1]))) ? " " : "_")
elsif cell & E != 0
print(((cell | row[x+1]) & S != 0) ? " " : "_")
else
print "|"
end
end
puts
end
end
# --------------------------------------------------------------------
# 5. Prim's algorithm
# --------------------------------------------------------------------
print "\e[2J" # clear the screen
mark(rand(width), rand(height), grid, frontier)
until frontier.empty?
x, y = frontier.delete_at(rand(frontier.length))
n = neighbors(x, y, grid)
nx, ny = n[rand(n.length)]
dir = direction(x, y, nx, ny)
grid[y][x] |= dir
grid[ny][nx] |= OPPOSITE[dir]
mark(x, y, grid, frontier)
display_maze(grid)
sleep 0.01
end
display_maze(grid)
# --------------------------------------------------------------------
# 6. Show the parameters used to build this maze, for repeatability
# --------------------------------------------------------------------
puts "#{$0} #{width} #{height} #{seed}"