Sequencing in situ by multiplexed padlock probes and rolling circle amplification (RCA)
Daniel Fürth
Meletis Lab
DMC lab meeting
9th May 2016
daniel.furth@ki.se
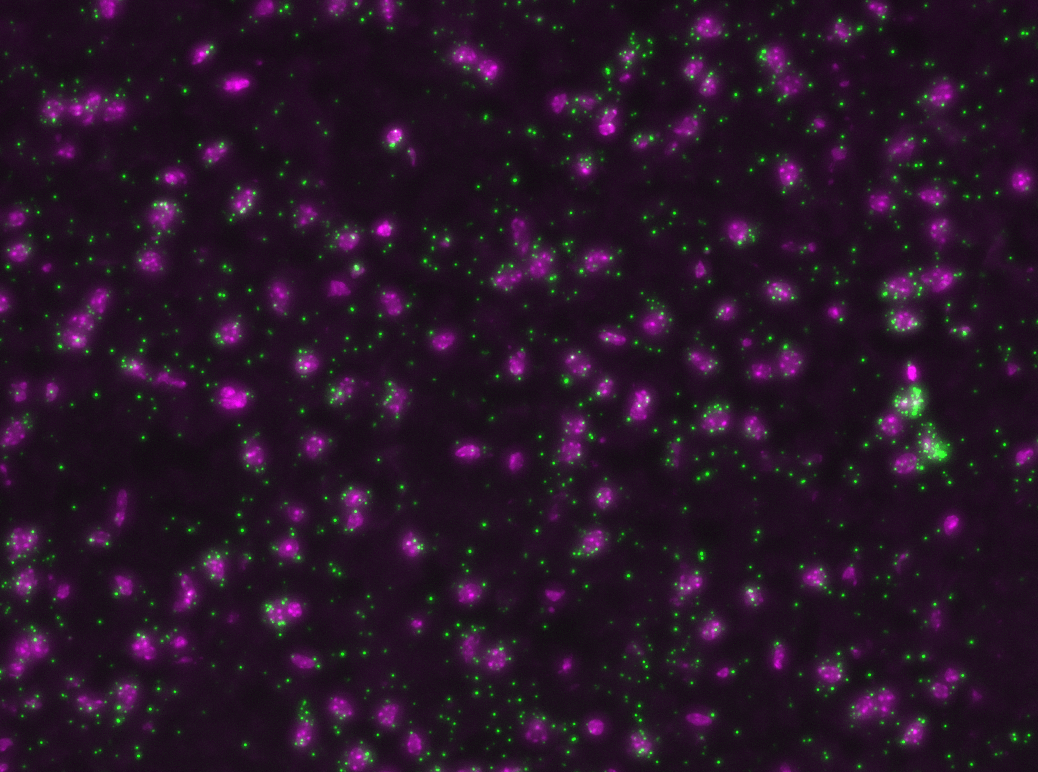
Padlock probes

b, b' : 20nt target sequences.
a, a' : complementary sequence.
c: detection sequence
linear, oligonucleotide single stranded construct construct
Nilsson et al. (1994) Science
Padlock probes

b, b' : 20nt target sequences.
a, a' : complementary sequence.
c: detection sequence
linear, oligonucleotide single stranded construct construct
5'

If last nt of the 3’ arm are non-complementary to the target sequence:
ligation is comprimised (padlock is not locked)
3'
5'
3'
Nilsson et al. (1994) Science
Rolling Circle Amplification (RCA)
If ligation is not comprimised padlock probe will not be washed away.
Phi29 DNA Polymerase yields 800-1000 copies of a padlock sequence per hour.
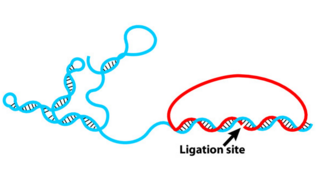
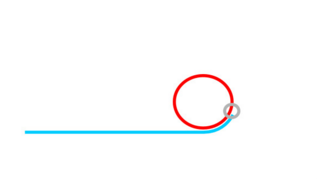
Rolling Circle Amplification (RCA)
If ligation is not comprimised padlock probe will not be washed away.
Phi29 DNA Polymerase yields 800-1000 copies of a padlock sequence per hour.

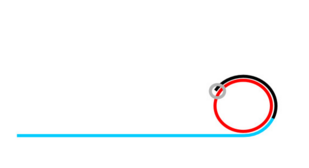
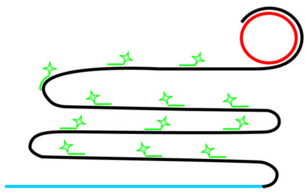
Rolling Circle Amplification (RCA)
If ligation is not comprimised padlock probe will not be washed away.
Phi29 DNA Polymerase yields 800-1000 copies of a padlock sequence per hour.




Multiplexing
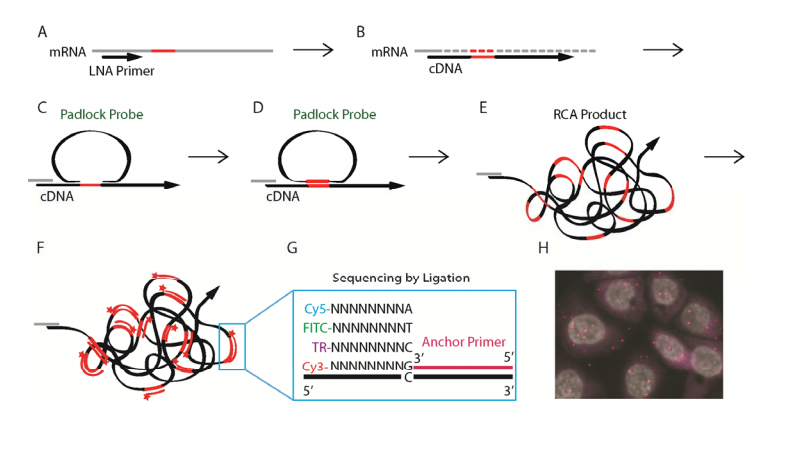
Reverse transcription
RNase H digestion
Hybridization
Ligation
Rolling Circle Amplification
FISH
Multiplexed padlock probes
Mats Nilsson and Jens Hjerling-Leffler
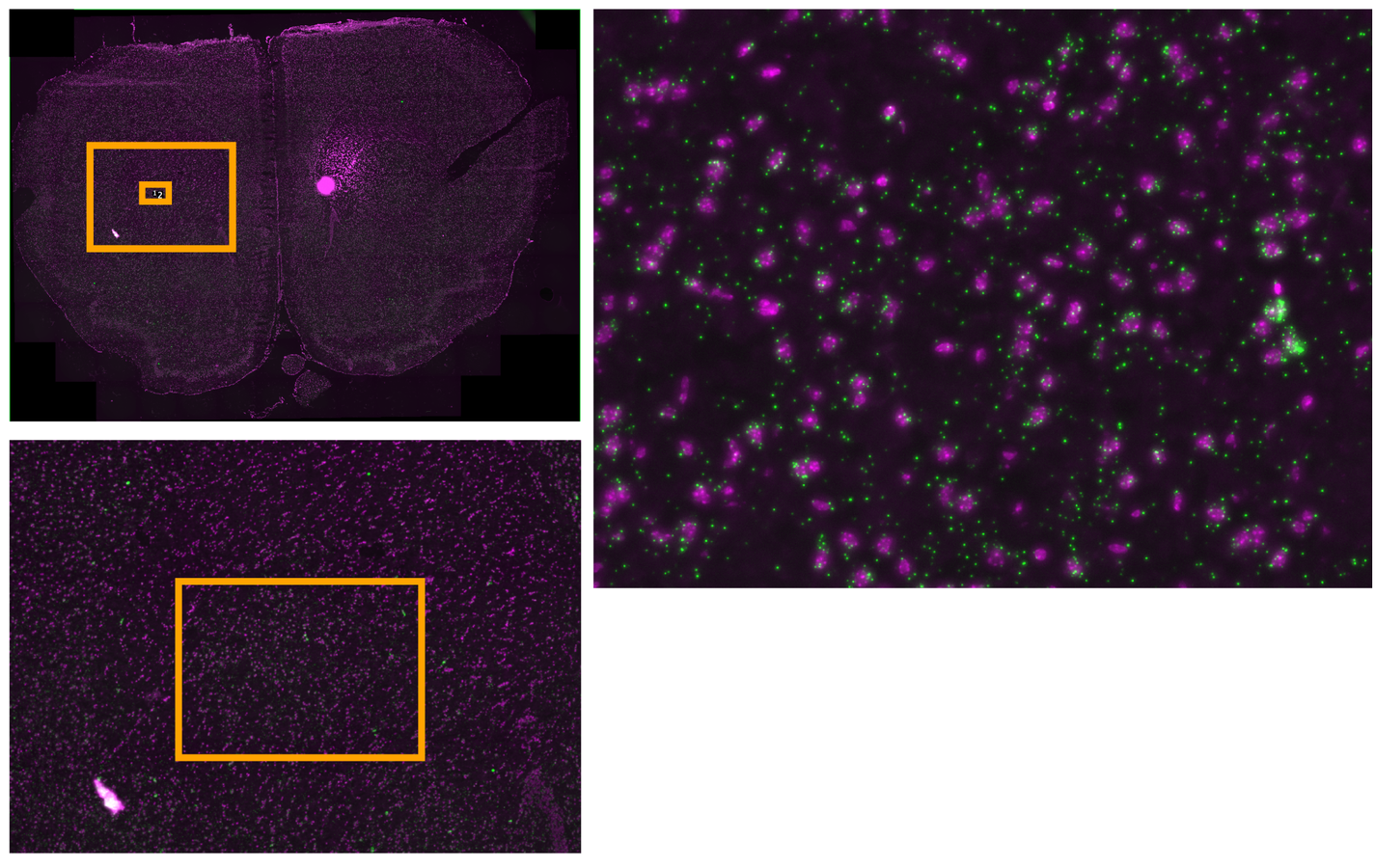
Multiplexed padlock probes
Mats Nilsson and Jens Hjerling-Leffler

Multiplexed padlock probes
Mats Nilsson

Multiplexed padlock probes
Mats Nilsson
Thank you!
Concurrency and parallel programming
- Multi-threaded applications through .

#include <string>
#include <iostream>
#include <thread>
using namespace std;
//The functions we want to make the thread run.
void task1(string msg)
{
cout << "task1 says: " << msg;
}
void task2(string msg)
{
cout << "task1 says: " << msg;
}
//Main loop.
int main()
{
thread t1(task1, "Task 1 executed");
thread t2(task2, "Task 1 executed");
//let main wait for t1 and t2 to finish.
t1.join();
t2.join();
}Rcpp

Dual core
Concurrency and parallel programming
- Multi threaded applications through .

#include <string>
#include <iostream>
#include <thread>
using namespace std;
//The functions we want to make the thread run.
void task1(string msg)
{
cout << "task1 says: " << msg;
}
void task2(string msg)
{
cout << "task1 says: " << msg;
}
//Main loop.
int main()
{
thread t1(task1, "Task 1 executed");
thread t2(task2, "Task 1 executed");
t1.join();
t2.join();
}Rcpp
Parallel computing
- Parallel computing is extremely simple to implement from R.
# install.packages('foreach'); install.packages('doSNOW')
library(foreach)
library(doSNOW)
cl <- makeCluster(2, type = "SOCK")
registerDoSNOW(cl)
getDoParName()
#matrix operators
x <- foreach(i=1:8, .combine='rbind', .packages='wholebrain' ) %:%
foreach(j=1:2, .combine='c', .packages='wholebrain' ) %dopar% {
l <- runif(1, i, 100)
i + j + l
}R package
- Why R?
- Standard data analysis:
- load some data
- estimate the density distribution.
- plot it
- Standard data analysis:
xx <- faithful$eruptions
fit <- density(xx)
plot(fit)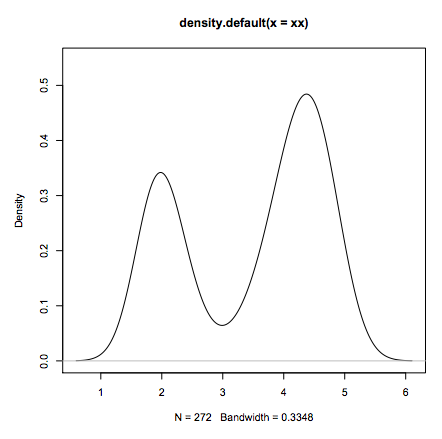
R package
- Why R?
#Line 1: loading
xx <- faithful$eruptions
#Line 2: estimate density
fit1 <- density(xx)
#Line 2: draw 10'000 bootstraps
fit2 <- replicate(10000, {
x <- sample(xx,replace=TRUE);
density(x, from=min(fit1$x), to=max(fit1$x))$y
})
#Line 3: compute 95% error "bars"
fit3 <- apply(fit2, 1, quantile,c(0.025,0.975))
#Line 4: plot the estimate
plot(fit1, ylim=range(fit3))
#Line 5: add estimation error as shaded region
polygon(c(fit1$x,rev(fit1$x)), c(fit3[1,], rev(fit3[2,])), col=’grey’, border=F)
#Line 6: add the line again since the polygon overshadows it.
lines(fit1)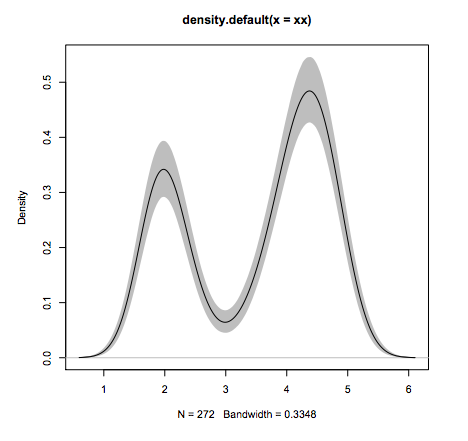
What other language can do this in 6 lines of code?
scRNA-seq
Gene specificity
about ~24'000 genes expressed in the brain.