Title Text
Curvature regularization with multigrid convergent estimator
Daniel Martins Antunes
Université Savoie Mont Blanc, LAMA
CoMeDic - ESIEE, Paris.
January 15, 2019
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Goal
Use curvature regularization in image processing tasks, i.e, inpainting, segmentation, stero.
segmentation
How?
Minimizing the energy functional
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
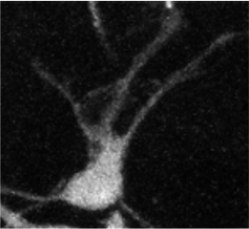



Data term
Data + Perimeter term
Data + Curvature term
[El-Zehiry, 2010]
Why curvature?
Completion property
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Why is it challenging?
Non-convex term
Difficult to optimize
Second order term. Should be careful with discretization scheme
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
MDCA + Graph-Cut
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
MDCA + Graph-Cut
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model









Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
MDCA + Graph-Cut




Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
MDCA + Graph-Cut
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
II + LP Relaxation
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
Grid cell representation
Binary variables for pixels
and linels
Consistency constraints
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
II + LP Relaxation
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
+ thresholding
linearization constraints
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Summary
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
MDCA + Graph cut: too local, generate many artifacts
II + LP: global optimization, but long running time
II + LP Relaxation: poor results
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Optimize digital boundary
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
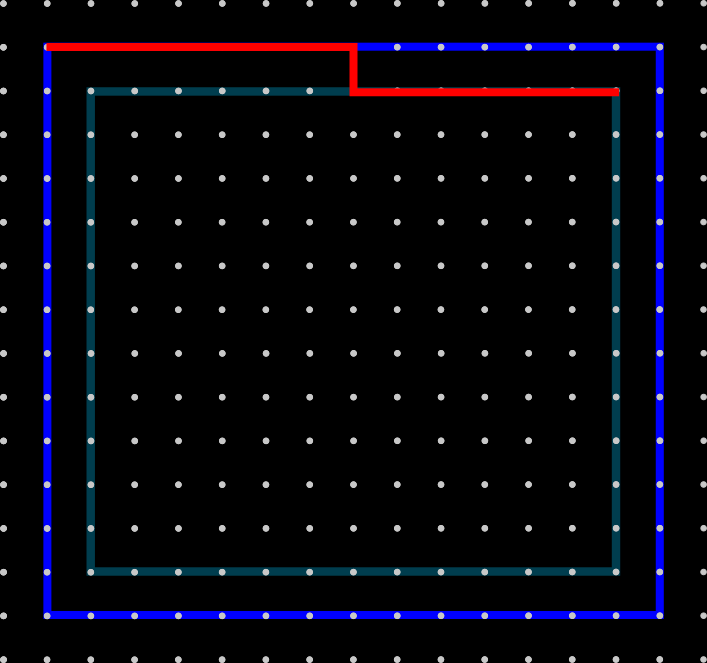
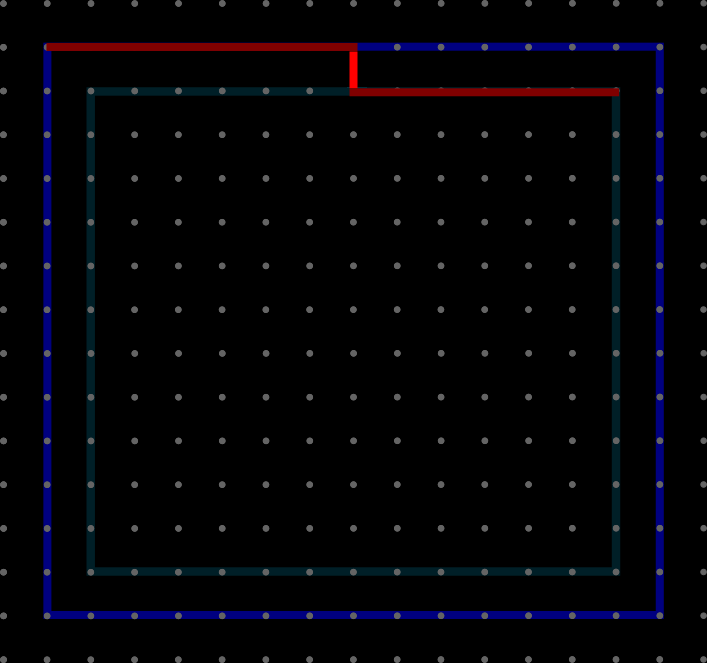
Optimization region
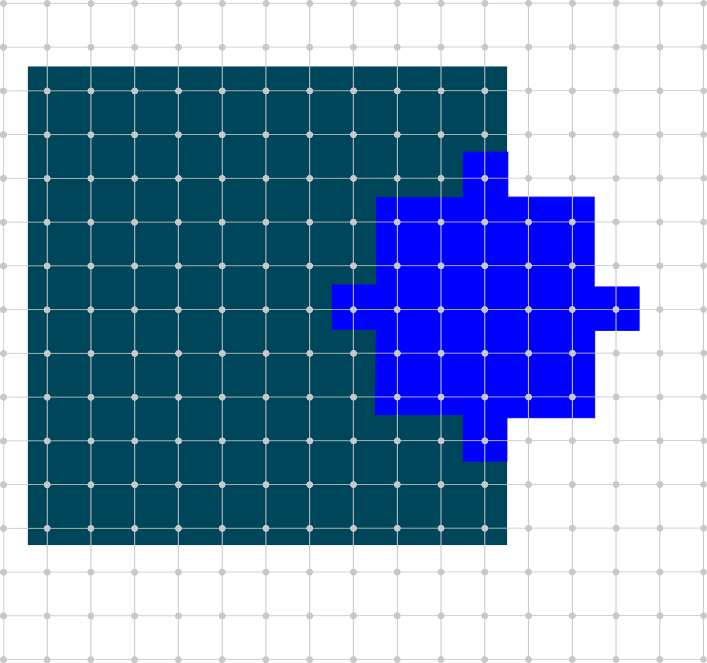
Symmetry issue
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Optimize digital boundary
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model
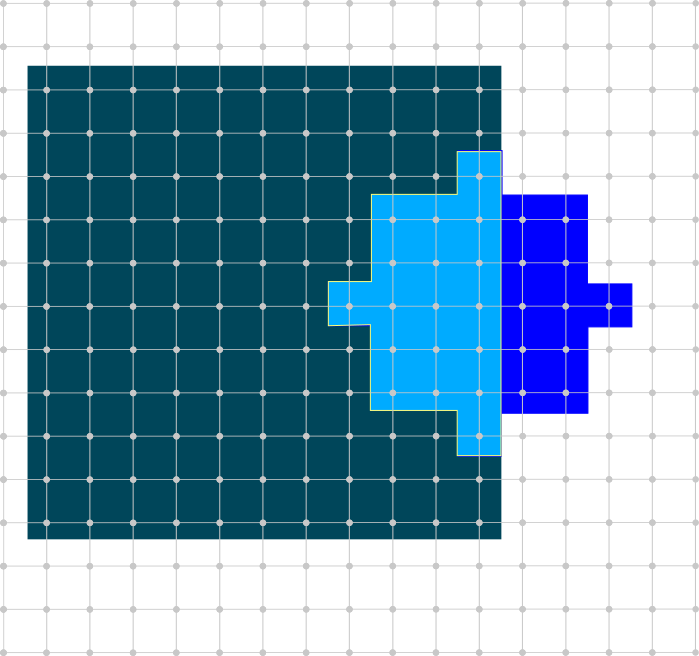
Optimization region
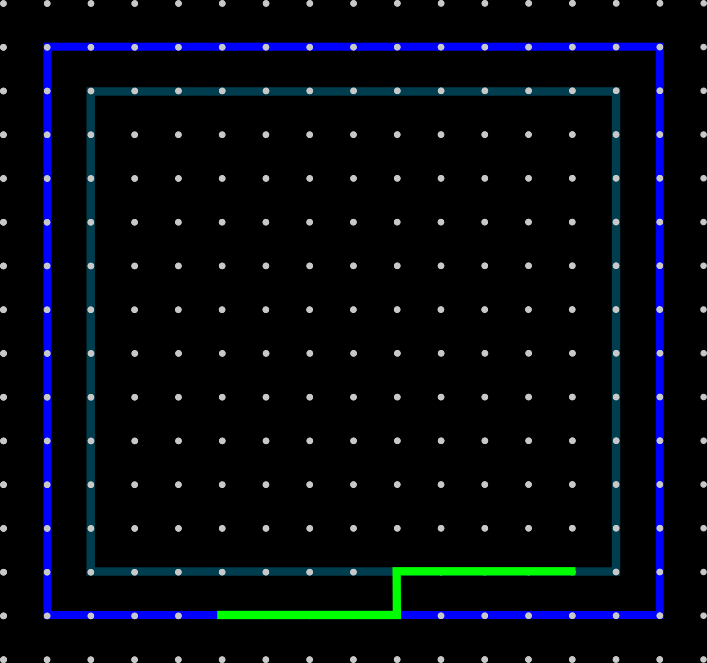
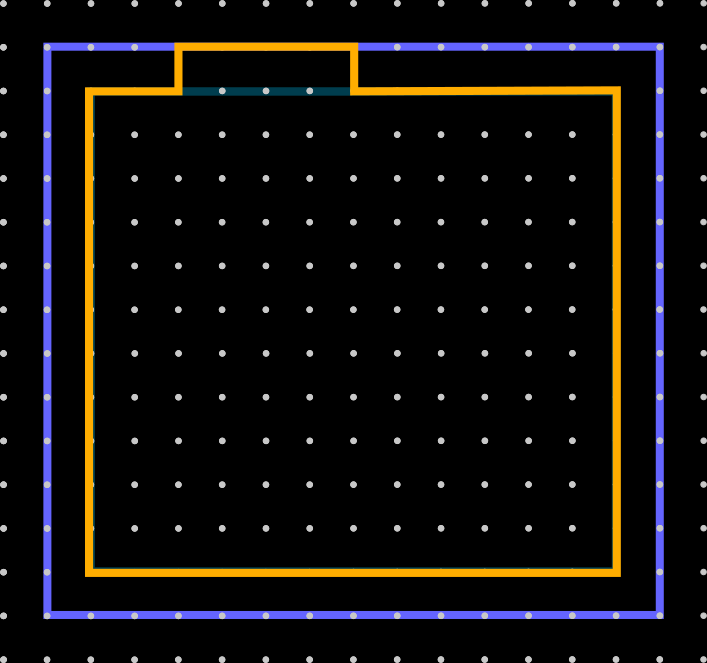
Estimator evaluation region
Solve using QPBOP
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Optimize digital boundary
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model


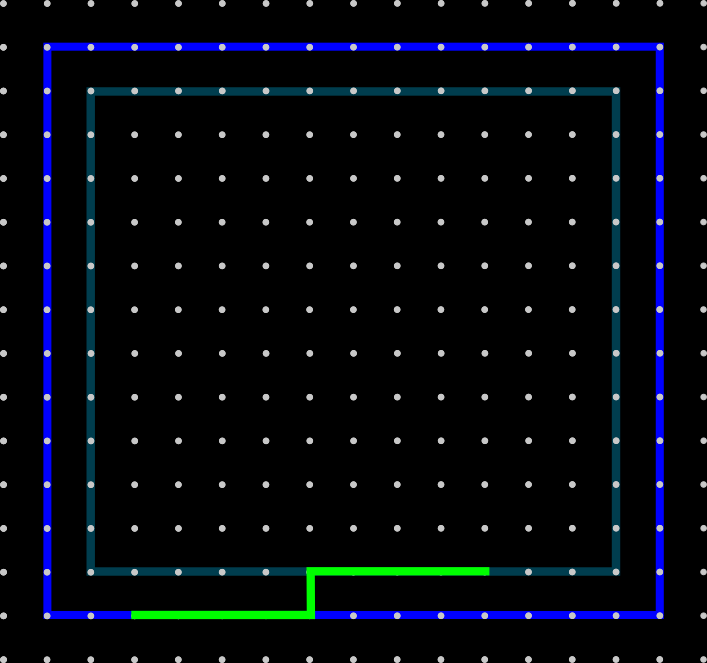
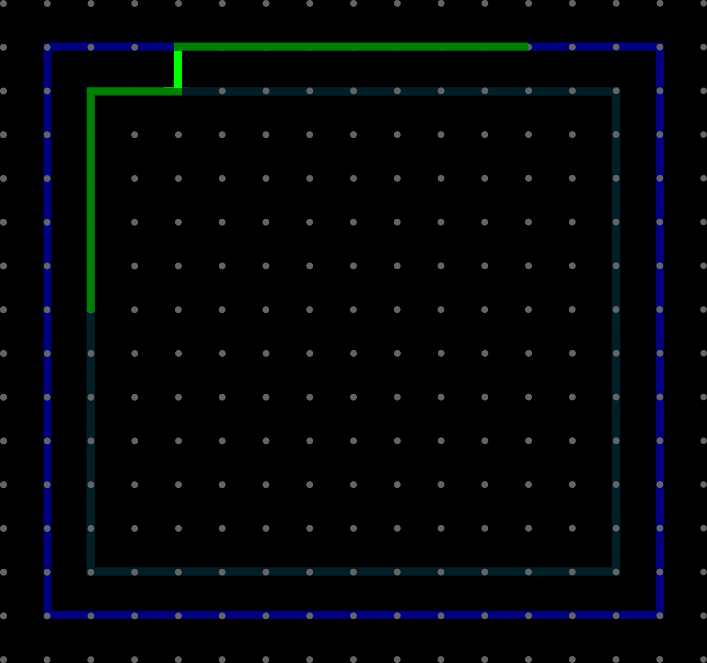
Labeled one pixel
Labeled zero pixel
Invert
solution
Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Optimize digital boundary
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model

Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Optimize digital boundary
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model

Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Boundary Regularization
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model




Daniel Martins Antunes
CoMeDiC - ESIEE, Paris. January 15, 2019
Boundary Regularization
Curvature regularization
with multigrid convergent estimator
Motivation
Modeling issues
Evolution model




