PyMKS Tutorial

Daniel Wheeler

My Background
- Computer Scientist at NIST
- Using Python since 2002
- Using/developing scientific software since 1995
- Dabble in machine learning ~4 years
- Software Carpentry instructor
PyMKS
- Materials Knowledge System
- Written in Python
- Provides machine learning techniques unavailable in other machine learning libraries
- Started in 2013
- 17 contributors
How does this work?
- What will we learn?
-
Live coding
-
Python?
-
Installation
-
Install on your laptop
-
Use Matin
-
Use Binder
-
-
Please stop me if I go too fast
-
Feel free to ask questions
What will we learn?
Classify Microstructures
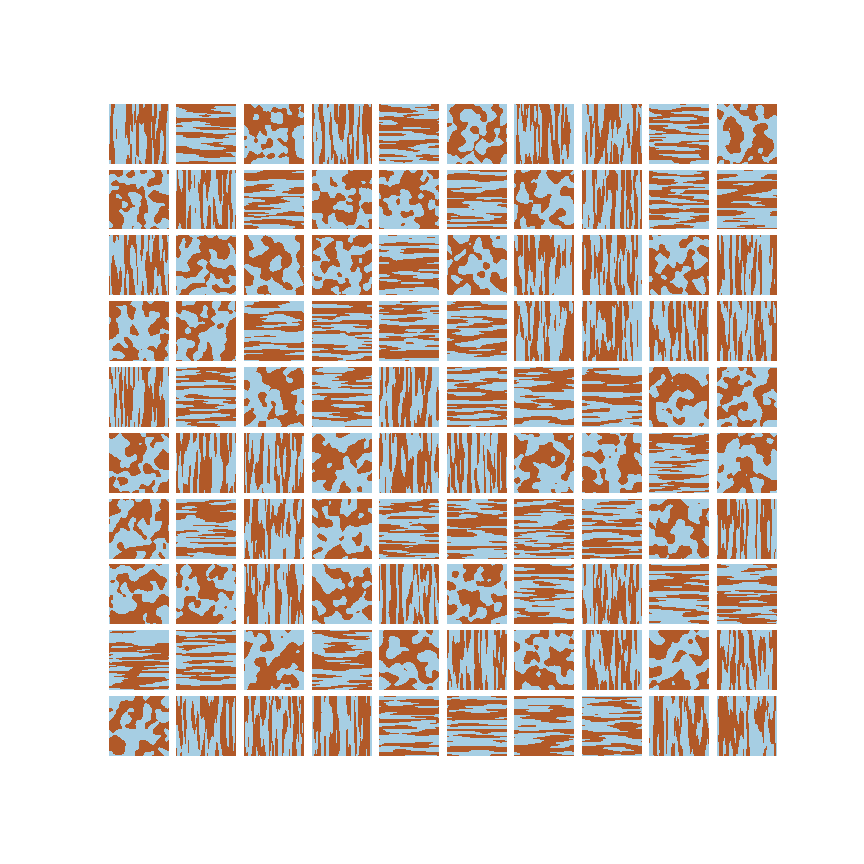


Metamodel
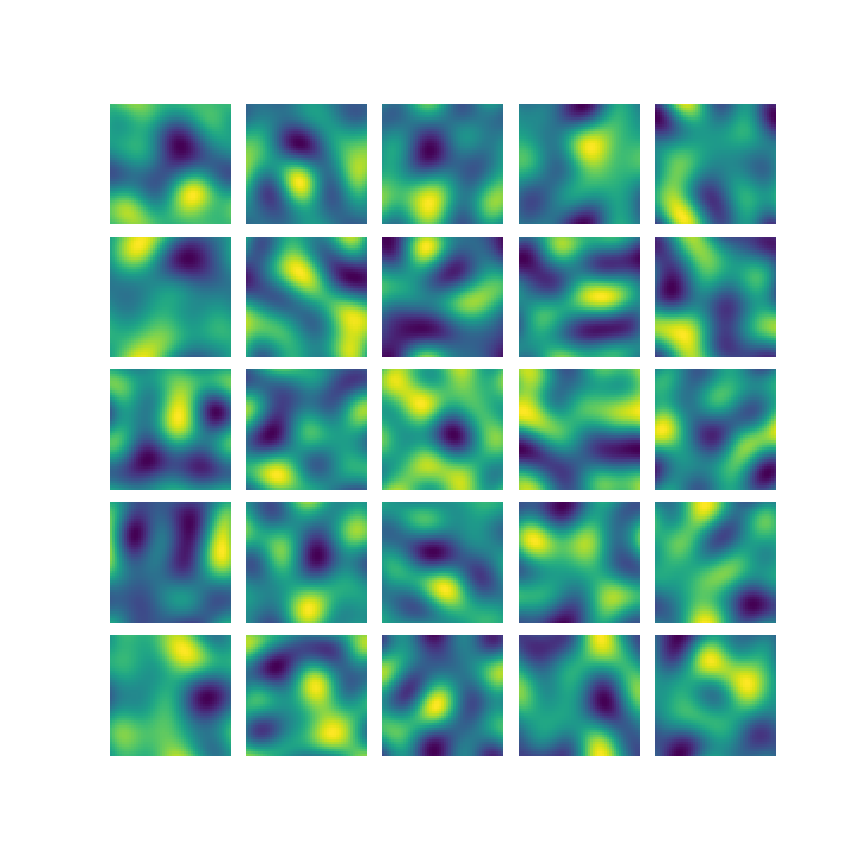


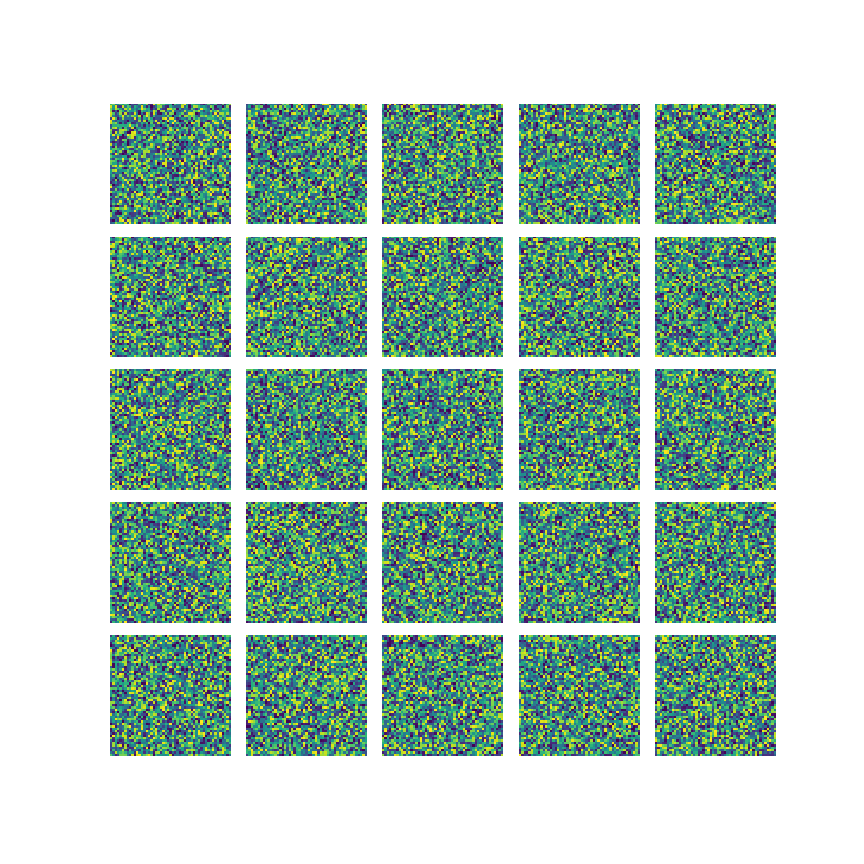
n \Delta t
model
metamodel
Homogenization

Localization


Microstructure
Response
1% displacement
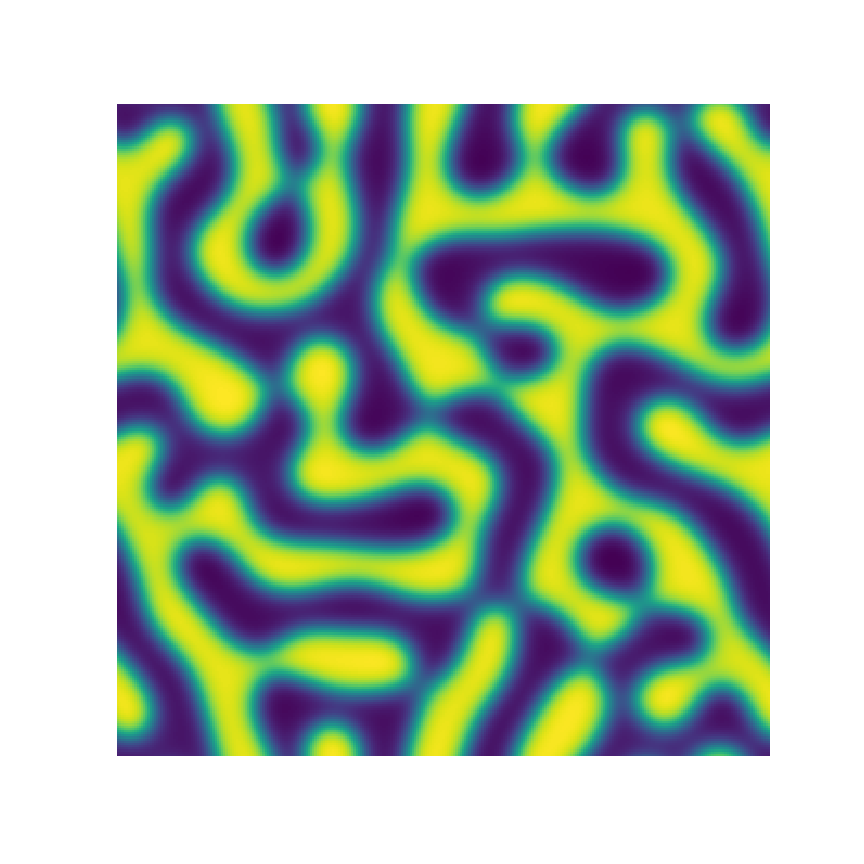
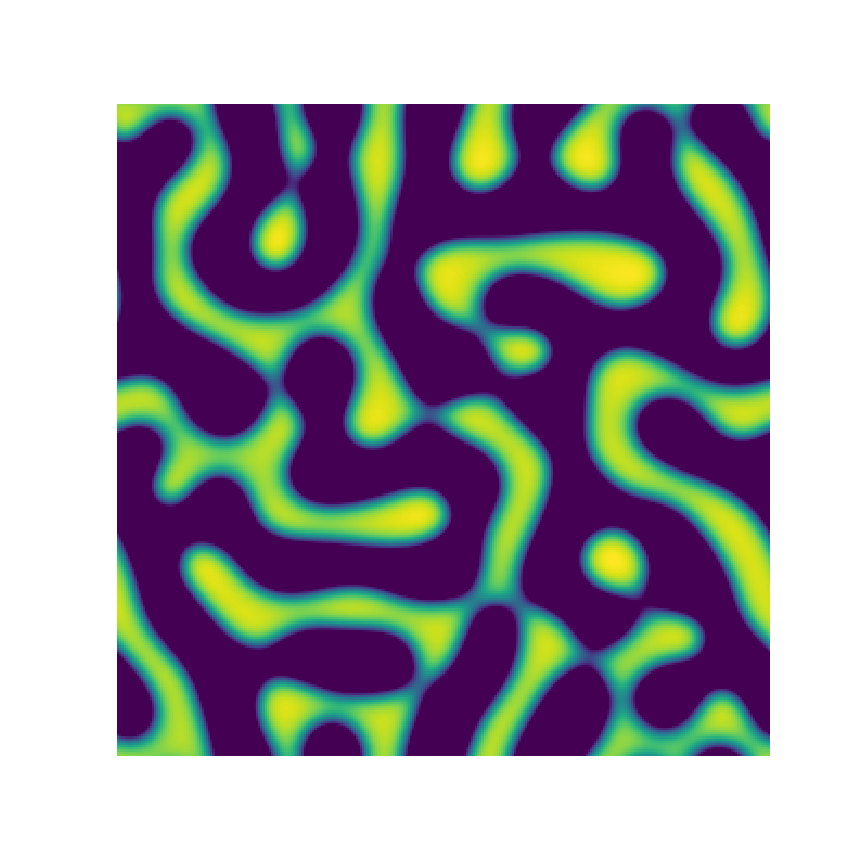
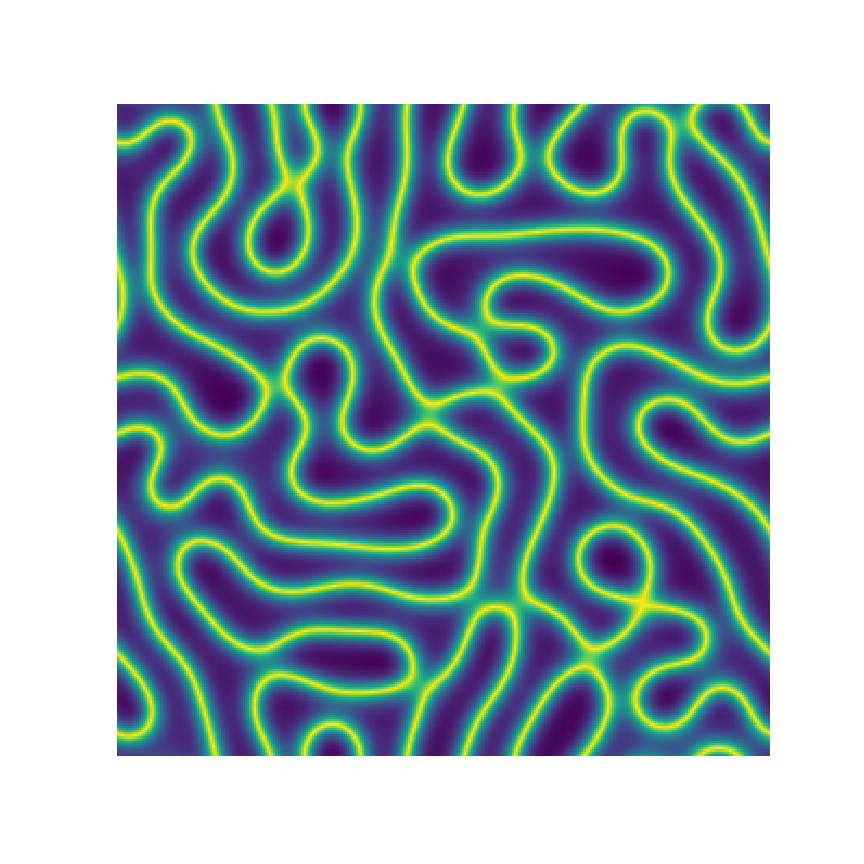

Channel 1
Channel 2
Channel 3
Microstructure Function
Microstructure Function
- Account for the stochastic nature of the local state
- Unified representation of the microstructure
- Create different mappings for different states
2-Point Statistics

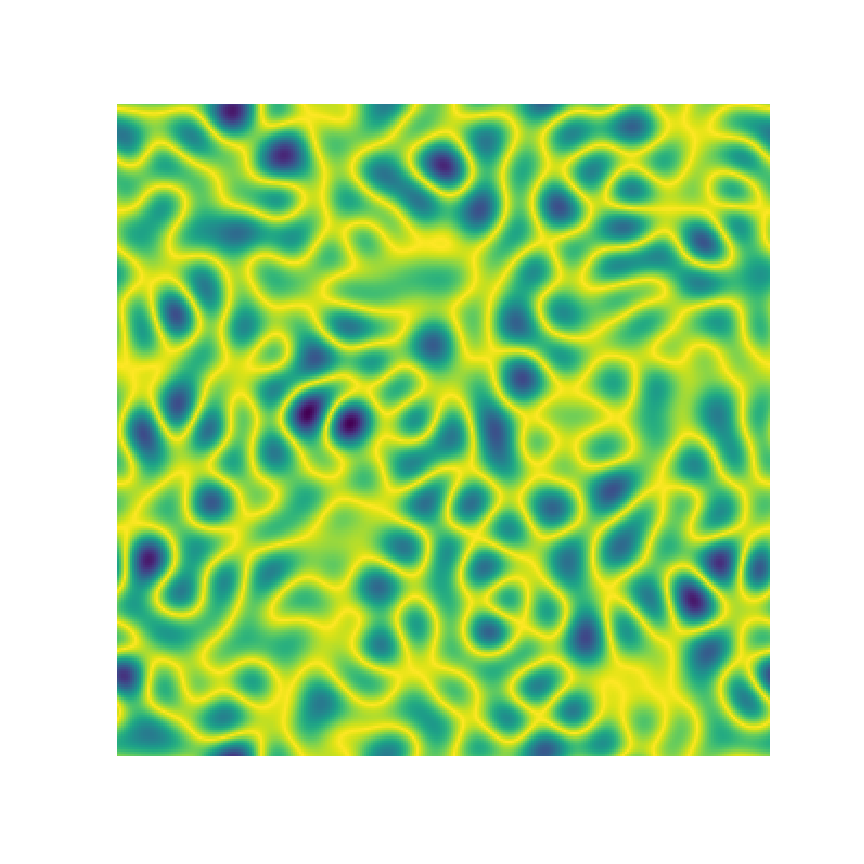

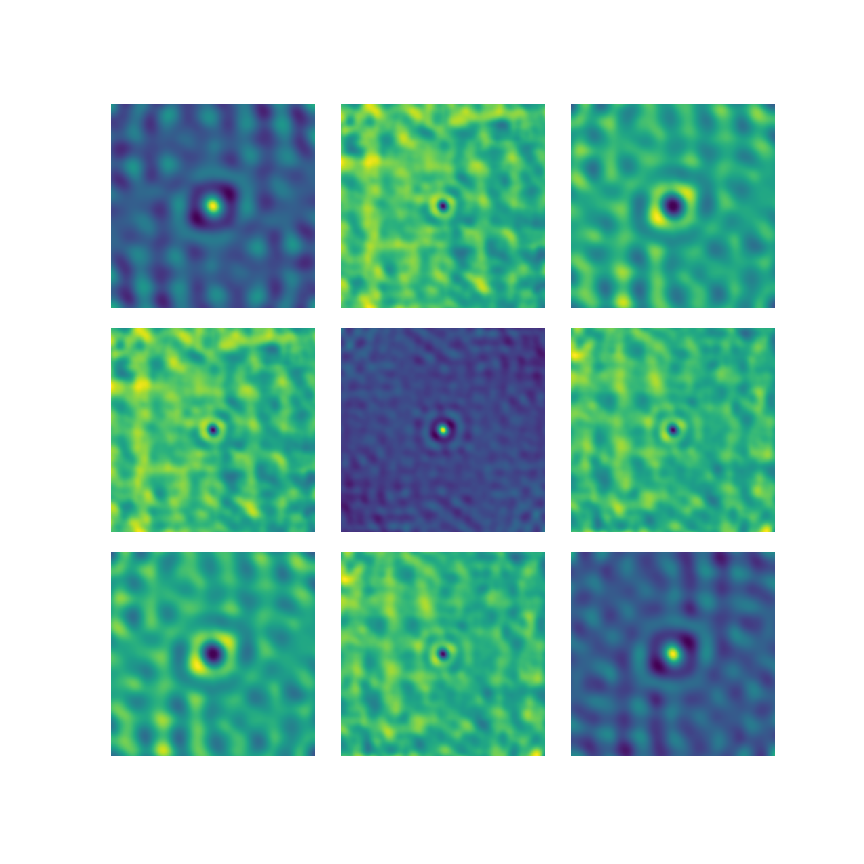

Samples v Features
\begin{pmatrix}
\begin{matrix}
m_{11} & m_{12} & \cdots & \cdots & \cdots & m_{1n} \\
m_{21} & m_{22} & \cdots & \cdots & \cdots & m_{2n} \\
\vdots & \vdots & \ddots & & & \vdots \\
\vdots & \vdots & & \ddots & & \vdots \\
\vdots & \vdots & & & \ddots & \vdots \\
m_{l1} & m_{l2} & \cdots & \cdots & \cdots & m_{ln}
\end{matrix}
\end{pmatrix}
\begin{pmatrix}
\begin{matrix}
r_{1} \\
r_{2} \\
\vdots \\
\vdots \\
\vdots \\
r_{l}
\end{matrix}
\end{pmatrix}
Samples
Features



Microstructure
Response
Make New Features
\begin{pmatrix}
\begin{matrix}
m_{11} & m_{12} & \cdots & \cdots & \cdots & m_{1n} \\
m_{21} & m_{22} & \cdots & \cdots & \cdots & m_{2n} \\
\vdots & \vdots & \ddots & & & \vdots \\
\vdots & \vdots & & \ddots & & \vdots \\
\vdots & \vdots & & & \ddots & \vdots \\
m_{l1} & m_{l2} & \cdots & \cdots & \cdots & m_{ln}
\end{matrix}
\end{pmatrix}





New features
n \gg l
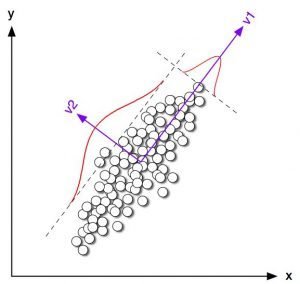
Dimensionality Reduction
\begin{pmatrix}
\begin{matrix}
m_{11} & m_{12} & \cdots & \cdots & \cdots & m_{1n} \\
m_{21} & m_{22} & \cdots & \cdots & \cdots & m_{2n} \\
\vdots & \vdots & \ddots & & & \vdots \\
\vdots & \vdots & & \ddots & & \vdots \\
\vdots & \vdots & & & \ddots & \vdots \\
m_{l1} & m_{l2} & \cdots & \cdots & \cdots & m_{ln}
\end{matrix}
\end{pmatrix}
Reduce features
l \gg n
n \gg l
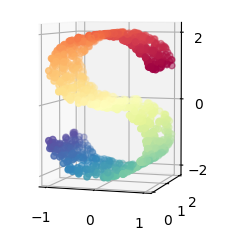
Learning
\begin{pmatrix}
\begin{matrix}
m_{11} & m_{12} & \cdots & \cdots & \cdots & m_{1n} \\
m_{21} & m_{22} & \cdots & \cdots & \cdots & m_{2n} \\
\vdots & \vdots & \ddots & & & \vdots \\
\vdots & \vdots & & \ddots & & \vdots \\
\vdots & \vdots & & & \ddots & \vdots \\
m_{l1} & m_{l2} & \cdots & \cdots & \cdots & m_{ln}
\end{matrix}
\end{pmatrix}
l \gg n
\begin{pmatrix}
\begin{matrix}
r_{1} \\
r_{2} \\
\vdots \\
\vdots \\
\vdots \\
r_{l}
\end{matrix}
\end{pmatrix}
Microstructure
Response
Microstructure

s = [0, 0]
s = [1, 0]
s = [2, 0]
s = [2, 1]
s = [1, 1]
s = [0, 1]
s = [0, 2]
s = [1, 2]
s = [2, 2]
\phi_k(\vec{s})
continuous:
discrete:
\phi_k[[i, j]]
\phi_k[[0, 0]] = 0
\phi_k[[0, 2]] = 1
categorical data
Microstructure
s = [0, 0]
s = [1, 0]
s = [2, 0]
s = [2, 1]
s = [1, 1]
s = [0, 1]
s = [0, 2]
s = [1, 2]
s = [2, 2]
\phi_k[[0, 1]] = 0.9
\phi_k[[0, 2]] = 0.1
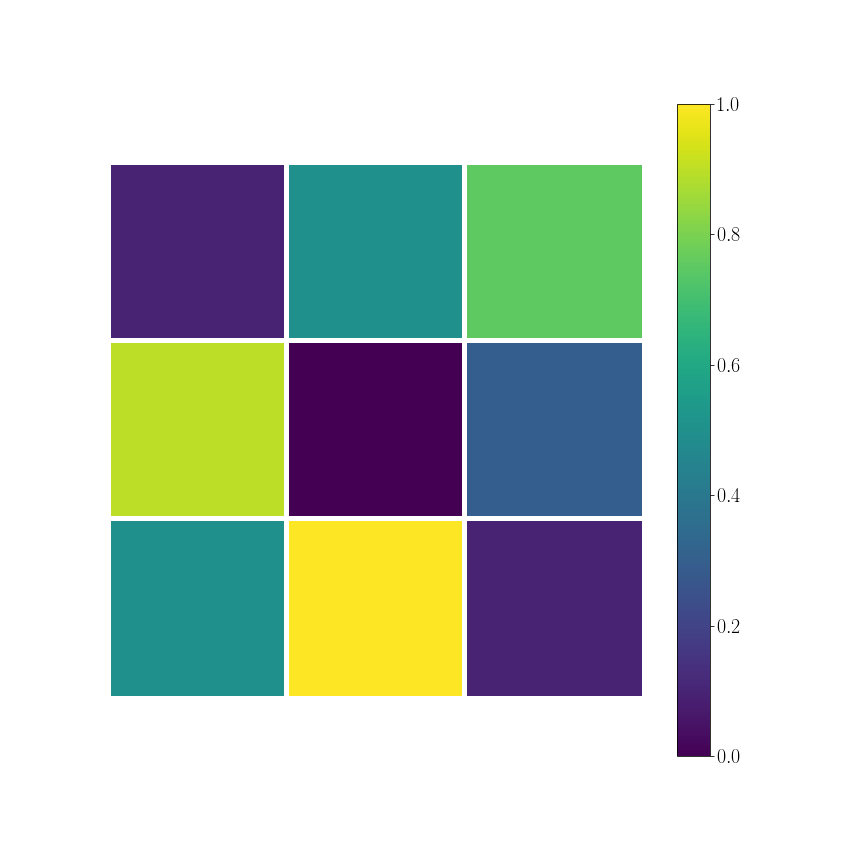
continuous data
Microstructure Function
\phi_k(\vec{s})
m_k(h; \vec{s})
\phi_k(\vec{s}) = \int_H h \; m_k(h; \vec{s}) \; dh
\int_H m_k(h; \vec{s}) \; dh = 1
m_k(h; \vec{s}) = \delta(h - \phi_k(\vec{s}))
Microstructure Function
\phi_k[s]
m_k[h; s]
m_k[h; s] = \delta[h - \phi_k[s]]
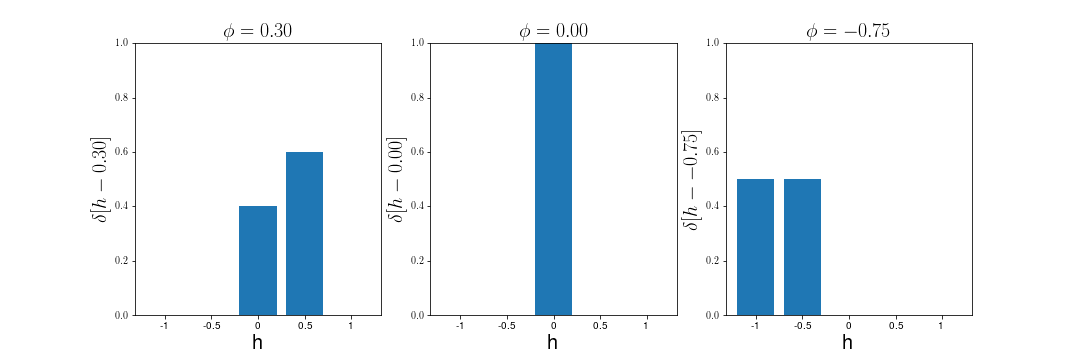
\delta [x] = \max \left( 1 - \left|\frac{x}{\Delta h}\right|, 0 \right)
Microstructure Function

s = [0, 0]
s = [1, 0]
s = [2, 0]
s = [2, 1]
s = [1, 1]
s = [0, 1]
s = [0, 2]
s = [1, 2]
s = [2, 2]
\phi_0[[0, 2]] = 1 \;\;\; m_0[0; [0, 2]] = 0
\phi_0[[0, 2]] = 1 \;\;\; m_0[1; [0, 2]] = 1
\phi_0[[0, 0]] = 0 \;\;\; m_0[0; [0, 0]] = 1
\phi_0[[0, 0]] = 0 \;\;\; m_0[1; [0, 0]] = 0
2-Point Stats

s = [0, 0]
s = [1, 0]
s = [2, 0]
s = [2, 1]
s = [1, 1]
s = [0, 1]
s = [0, 2]
s = [1, 2]
s = [2, 2]
f_k[h, h';r] = \frac{1}{\Omega_j[s]} \sum_{s \in S} m_k[h; s] m_k[h'; s + r]
f_0[0, 0; [0, 0]] = 5 / 9
f_0[1, 1; [0, 0]] = 4 / 9
f_0[0, 1; [0, 0]] = 0 / 9
f_0[1, 0; [2, -1]] = 3 / 9
f_0[1, 1; [2, -1]] = 1 / 9