Learning Hamiltonians of constrained mechanical systems
Davide Murari
One day – Young Researchers Seminars, Maths Applications & Models

\(\texttt{davide.murari@ntnu.no}\)
Joint work with Elena Celledoni, Andrea Leone and Brynjulf Owren
Definition of the problem
GOAL : approximate the unknown \(f\) on \(\Omega\)
DATA:
Approximation of a dynamical system
Introduce a parametric model
1️⃣
3️⃣
Choose any numerical integrator applied to \(\hat{f}_{\theta}\)
2️⃣
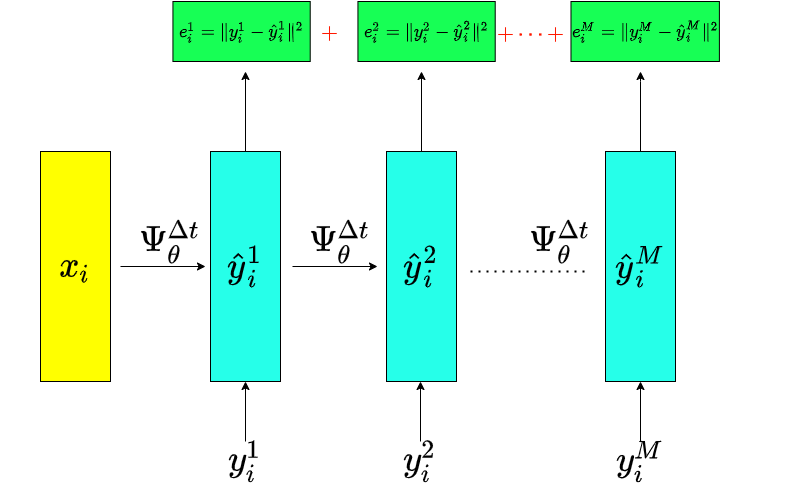
Unconstrained Hamiltonian systems
Unconstrained Hamiltonian systems
Choice of the model:
\(Net_{\bar{\theta}}(q)\)
Measuring the approximation quality
Test initial conditions
Numerical experiment
⚠️ The integrator used in the test, can be different from the training one.
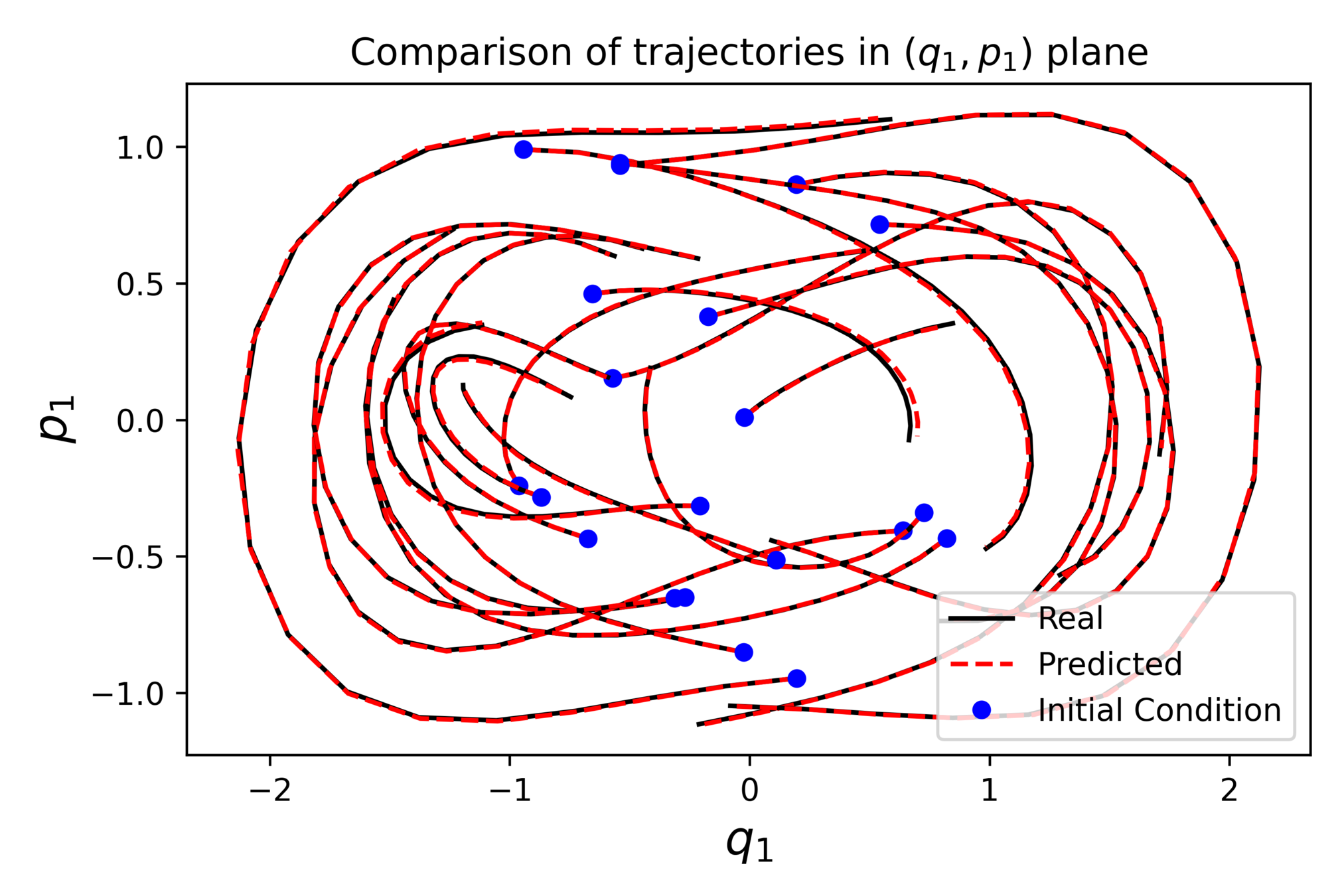
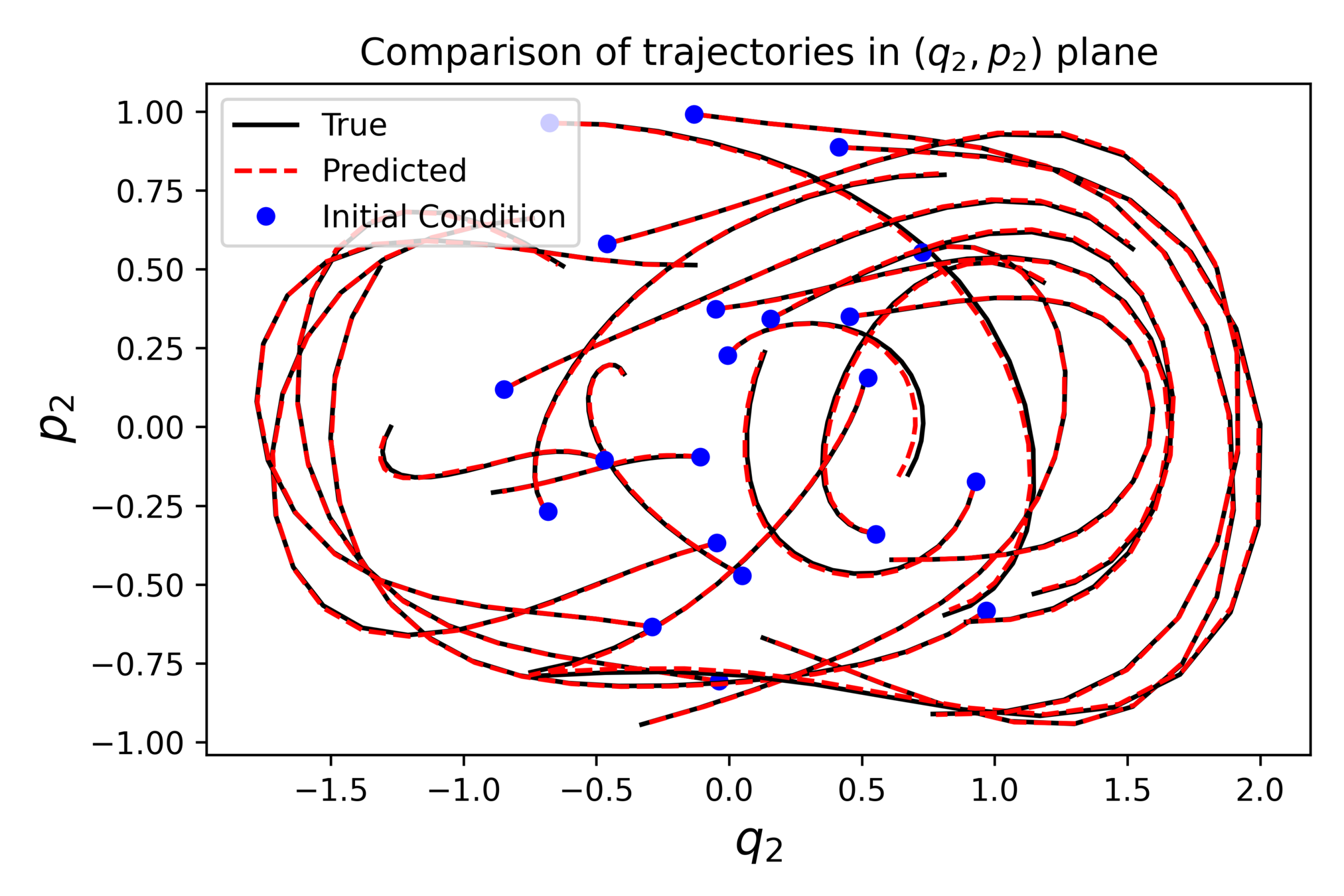
Constrained Hamiltonian systems
Modelling the vector field on \(\mathcal{M}\)
On \(\mathcal{M}\) the dynamics can be written as
⚠️ On \(\mathbb{R}^{2n}\setminus\mathcal{M}\) the vector field extends non-uniquely.
Learning constrained Hamiltonian systems
Example with the double spherical pendulum
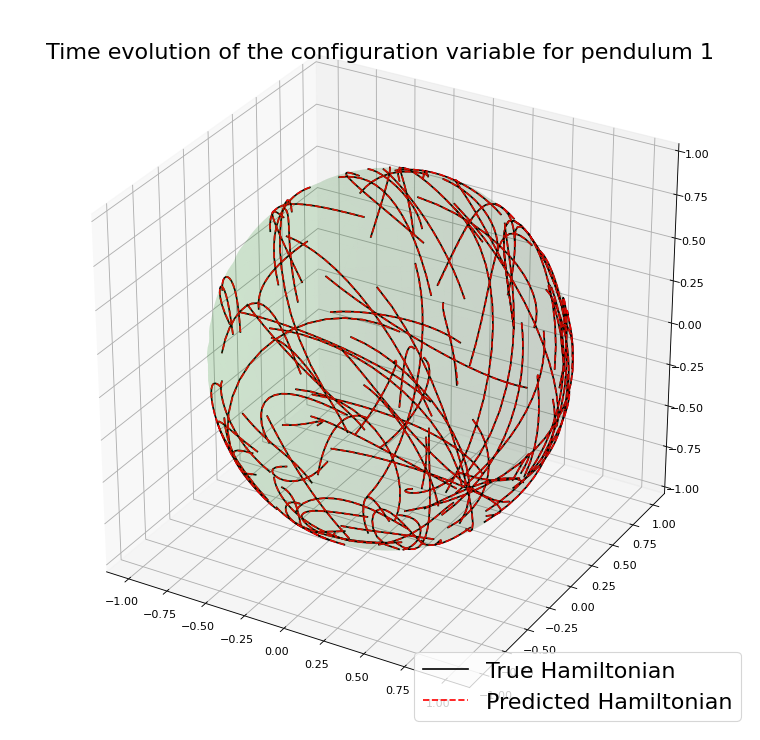
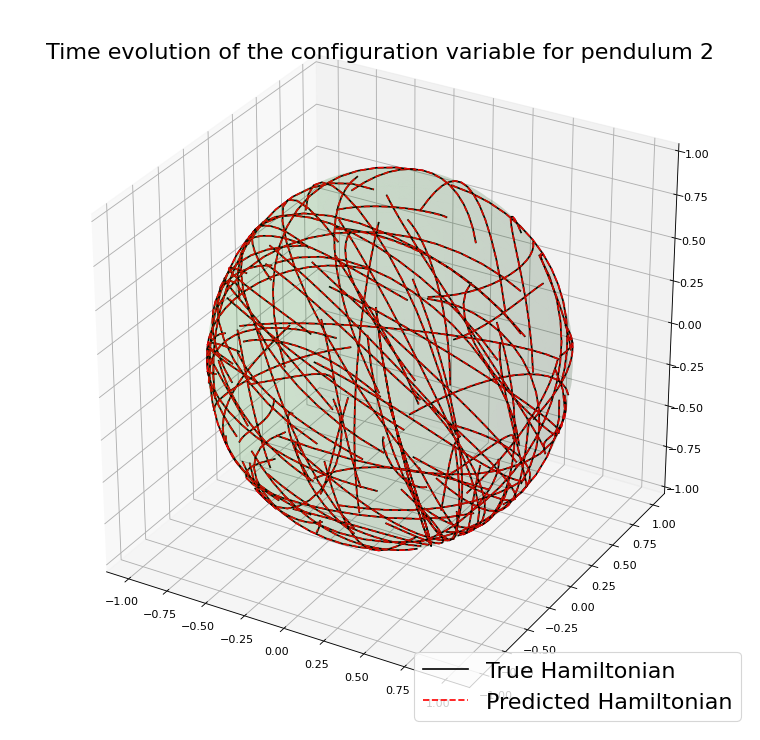
A case where preserving \(\mathcal{M}\) helps
Suppose to have just few unknown elements in the expression of the Hamiltonian
As a consequence, one expects a very accurate approximation.
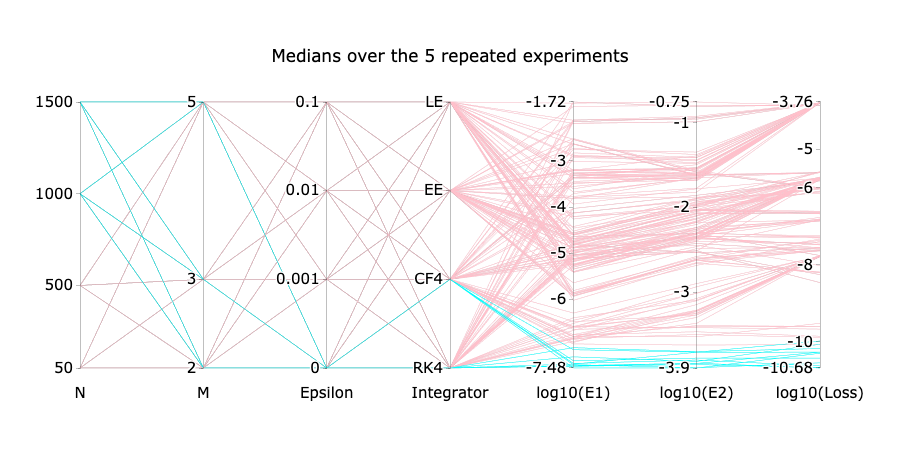
Example with the spherical pendulum:

Similar results preserving \(\mathcal{M}\)
For interactive plots complementary
to this:


Thank you for the attention
Preprint:
Celledoni, E., Leone, A., Murari, D., & Owren, B. (2022). Learning Hamiltonians of constrained mechanical systems. arXiv preprint arXiv:2201.13254