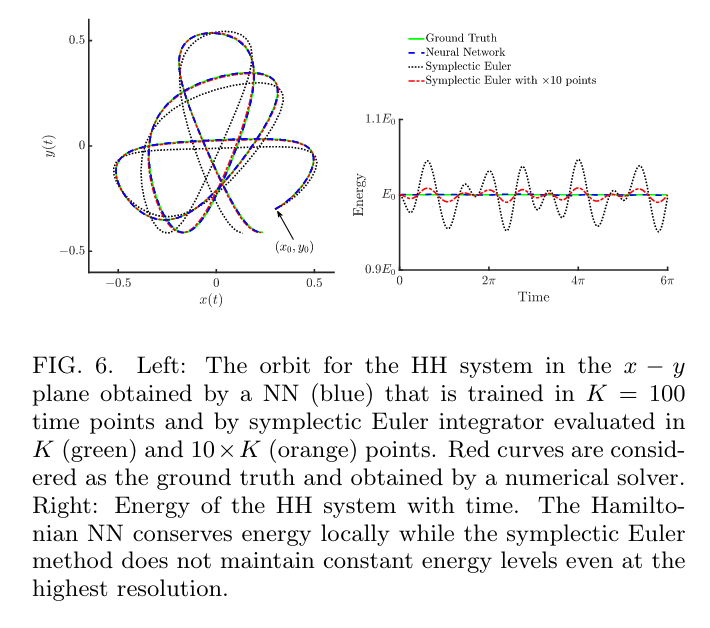
Hamiltonian NNs for equations of motion

Motivation

Hamiltonian NNs

Symplectic methods

Conserve a modified energy over long time

Conserve the correct energy over long time

Being iterative methods they accumulate errors

Provide smooth representation of the solution, not based on previous positions.

High cost to solve large systems

It was shown this does not happen for NN differential equation solvers

Being iterative methods they accumulate errors

Hamiltonian neural networks

GOAL: Solve for $t\in [0,T]$ the known system

\dot{z}(t) = \mathbb{J}\nabla H(z(t)),\,\, H:\mathbb{R}^{2n}\rightarrow\mathbb{R}\\ \mathbb{J} = \begin{bmatrix} 0_n & I_n \\ -I_n & 0_n \end{bmatrix}

STRATEGY: Model the solution with a network defined as

\hat{z}_{\theta}(t) = z_0 + f(t)\mathcal{N}_{\theta}(t)\in\mathbb{R}^{2n},\\ f:\mathbb{R}\rightarrow\mathbb{R},\,\, f(0)=0

Training

\hat{z}_{\theta}(t) = z_0 + f(t)\mathcal{N}_{\theta}(t)\in\mathbb{R}^{2n},\\ f:\mathbb{R}\rightarrow\mathbb{R},\,\, f(0)=0

Introduce a temporal discretization

$t_0=0<t_1<...<t_M=T$

Then minimize the following loss function:

L=\frac{1}{M} \sum_{n=1}^M\left(\dot{\hat{z}}_n-\mathbb{J}\nabla_{\hat{z}_n} H\left(\hat{z}_n\right)\right)^2+\lambda L_{\mathrm{reg}}

with $\hat{z}_n := \hat{z}(t_n)$ and $\dot{\hat{z}}_n := \frac{d}{dt}\hat{z}(t)\vert_{t=t_n}$

Training

L=\frac{1}{M} \sum_{n=1}^M\left(\dot{\hat{z}}_n-\mathbb{J}\nabla_{\hat{z}_n} H\left(\hat{z}_n\right)\right)^2+\lambda L_{\mathrm{reg}}

with $\hat{z}_n := \hat{z}(t_n)$ and $\dot{\hat{z}}_n := \frac{d}{dt}\hat{z}(t)\vert_{t=t_n}$

L_{\mathrm{reg}}=\frac{1}{M} \sum_{n=1}^M\left[\left(H\left(\hat{z}_n\right)-H\left(z_0\right)\right)^2\right]

Choice of $f(t)$

They use the function $f(t) = 1-e^{-t}$

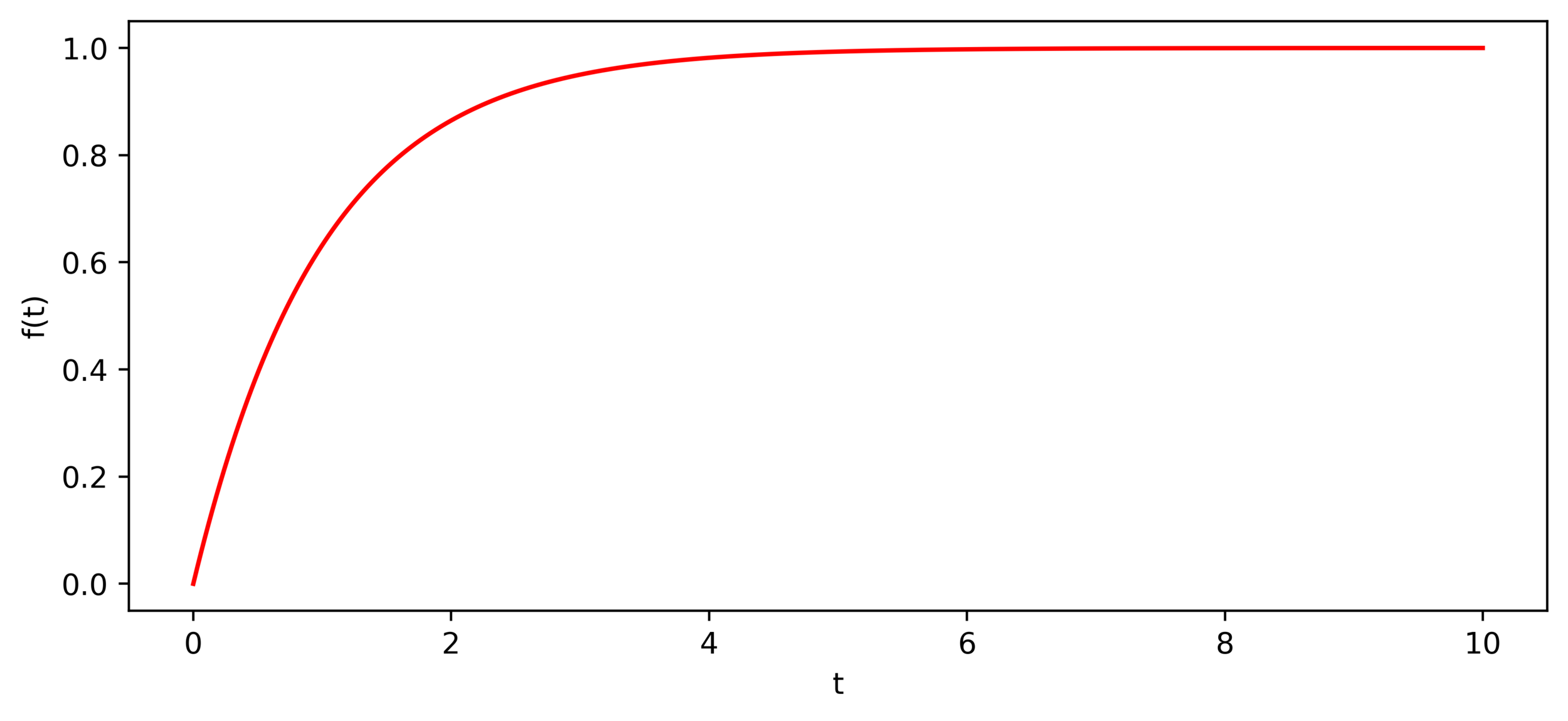
$f$ rapidly tends to $1$ and hence when $\lambda=0$, for long enough time not just $\hat{z}(t)$ will be symplectic but also $\mathcal{N}_{\theta}(t)$ since

\hat{z}_{\theta}(t) = z_0 + f(t)\mathcal{N}_{\theta}(t)\in\mathbb{R}^{2n}

Error analysis

$\delta z_n:= z(t_n)-\hat{z}(t_n)\in\mathbb{R}^{2n}$

$ H(z_n) \approx H(\hat{z}_n) + \nabla H(\hat{z}_n) \delta z_n+ \frac{1}{2}\delta z_n^T \nabla^2H(\hat{z}_n)\delta z_n$

$\nabla H(\hat{z}_n) \approx \nabla H(z_n) - \nabla^2 H(\hat{z}_n)\delta z_n$

\ell_n:=\dot{\hat{z}}_n-\mathbb{J}\nabla H(\hat{z}_n)\\ \approx \dot{\hat{z}}_n-\mathbb{J}\left(\nabla H(z_n)-\nabla^2 H(\hat{z}_n)\delta z_n\right)\\ =-\delta\dot{z}_n+\mathbb{J}\nabla^2H(z_n)\delta z_n

This gives an ODE for the error, once we have $\ell(t)$

Error analysis

\ell_n\approx \mathbb{J}\nabla^2H(z_n)\delta z_n-\delta\dot{z}_n

suppose $\bar{\ell}\geq \ell_n$ for every $n$

Suppose $\delta z_n$ is the maximum value and $\delta z_n = (0,...,0,\delta z_n^i,0,...,0)$

Then we have

$$|\delta z_n^i |\leq \frac{\bar{\ell}}{\sigma_{min}}$$

where $\sigma_{min}$ is the minimum singular value of $\nabla^2H(\hat{z}_n)$

Hénon-Heiles system

H(z)=\frac{1}{2}\left(p_x^2+p_y^2\right)+\frac{1}{2}\left(x^2+y^2\right)+\left(x^2 y-\frac{y^3}{3}\right)

Hénon-Heiles system