ECMI 2023

Learning Hamiltonians of constrained mechanical systems

Davide Murari

ECMI Conference, Wrocław, 2023

\(\texttt{davide.murari@ntnu.no}\)

Joint work with Elena Celledoni, Andrea Leone and Brynjulf Owren

Definition of the problem

\dot{x}(t) = f(x(t))\in\mathbb{R}^n

GOAL : approximate the unknown \(f\) on \(\Omega\)

DATA:

\{(x_i,y_i^1,...,y_i^M)\}_{i=1,...,N},\\ x_i\in\Omega\subset\mathbb{R}^n

y_i^j = \Phi_f^{j\Delta t}(x_i) + \delta_i^j

\Delta t>0

Approximation of a dynamical system

Introduce a parametric model

\dot{x}(t) = \hat{f}_{\theta}(x(t))

\text{solve}\quad \min_{\theta} \sum_{i=1}^N \sum_{j=1}^M \left\|y_i^j - \hat{y}_i^{j}\right\|^2 = \min_{\theta}\mathcal{L}_{\theta}

1️⃣

3️⃣

Choose any numerical integrator applied to \(\hat{f}_{\theta}\)

\hat{y}_i^0 = x_i,\,\,\hat{y}_i^{j+1} = \Psi_{\theta}^{\Delta t}(\hat{y}_i^{j})

2️⃣

Constrained Hamiltonian systems

\begin{cases} \dot{y}(t) = \mathbb{J}\nabla H(y(t)),\quad y=(q,p)\\ g(q) = 0,\quad g:\mathbb{R}^n\rightarrow\mathbb{R}^m \end{cases}

\mathcal{M} = T^*\mathcal{Q}=T^*\{q\in\mathbb{R}^n:\,g(q)=0\} = \\ \{(q,p)\in\mathbb{R}^{2n}:\,g(q)=0,\,G(q)\partial_pH(q,p)=0\}

\mathcal{Q}=\{q\in\mathbb{R}^n:\;g(q)=0\}\subset\mathbb{R}^n

Modelling the vector field on \(\mathcal{M}\)

P(q) : \mathbb{R}^n\rightarrow T_q\mathcal{Q},\,v\mapsto P(q)v

T_q\mathcal{Q} = \{v\in\mathbb{R}^n:\,G(q)v=0\}

\begin{cases} \dot{q}=P(q) \partial_{p} H(q, p) \\ \dot{p}=-P(q)^{T} \partial_{q} H(q, p)+W(q, p) \partial_{p} H(q, p) \end{cases}

On \(\mathcal{M}\) the dynamics can be written as

With \(W(q,p)\equiv 0\) when \(P(q)=I\).

⚠️ On \(\mathbb{R}^{2n}\setminus\mathcal{M}\) the vector field extends non-uniquely.

Learning constrained Hamiltonian systems

\hat{f}_{\theta}(q,p) = \begin{bmatrix} P(q) \partial_{p} H_{\theta}(q, p) \\ -P(q)^{T} \partial_{q} H_{\theta}(q, p)+W(q, p) \partial_{p} H_{\theta}(q, p) \end{bmatrix}

H_{\theta}(q, p)=\frac{1}{2} p^{T} M_{\theta_{1}}^{-1}(q) p+\mathcal{N}_{\theta_{2}}(q),\\ \mathcal{N}_{\theta_{2}} = F_{\theta_{2,L}} \circ ... \circ F_{\theta_{2,1}}\\ F_{\theta_{2,i}}(q) = A^T_i\tanh(B_iq+b_i)

Measuring the approximation quality

\mathcal{E}_1 = \sum_{i=1}^{\bar{N}}\sum_{j=1}^{\bar{M}}\left\|y_i^j - \hat{y}_i^j\right\|^2

y_i^{j+1} = \tilde{\Psi}^{\Delta t}_{H}(y_i^j),\quad \hat{y}_i^{j+1} = \tilde{\Psi}^{\Delta t}_{H_{\theta}}(\hat{y}_i^j)

\mathcal{E}_{2}=\frac{1}{\bar{N}} \sum_{i=1}^{\bar{N}}\left|H\left(\bar{x}_{i}\right)-H_{\theta}\left(\bar{x}_{i}\right)-\mathcal{A}\right|\\ \mathcal{A} = \frac{1}{\bar{N}} \sum_{l=1}^{\bar{N}}\left(H\left(\bar{x}_{l}\right)-H_{\theta}\left(\bar{x}_{l}\right)\right)

\hat{y}_i^0 = y_i^0 = \bar{x}_i

Test initial conditions

A few words on the choice of the integrator

\mathcal{M}

x_i

\Psi_1^{\Delta t}(x_i)

\Psi_2^{\Delta t}(x_i)

A case where preserving \(\mathcal{M}\) helps

Suppose to have just few unknown elements in the expression of the Hamiltonian

As a consequence, one expects a very accurate approximation.

Example with the spherical pendulum:

H_{\theta}(q, p)=\frac{1}{2 m} p^{T} p+u^{T} q, \quad m>0, u \in \mathbb{R}^{3}

Similar results preserving \(\mathcal{M}\)

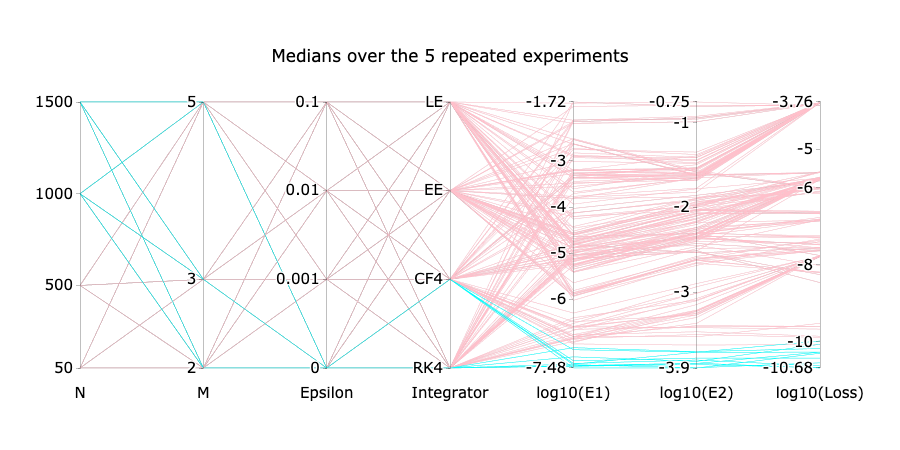
Scan for an interactive

version of the plot

Thank you for the attention

Celledoni, E., Leone, A., Murari, D., & Owren, B. (2023). Learning Hamiltonians of constrained mechanical systems. Journal of Computational and Applied Mathematics, 417, 114608.

Example with the double spherical pendulum

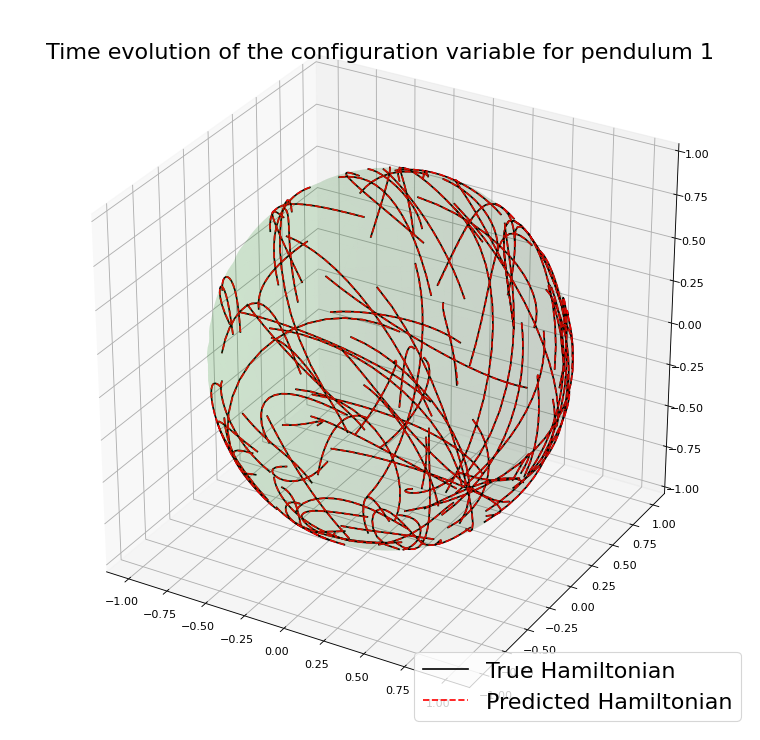
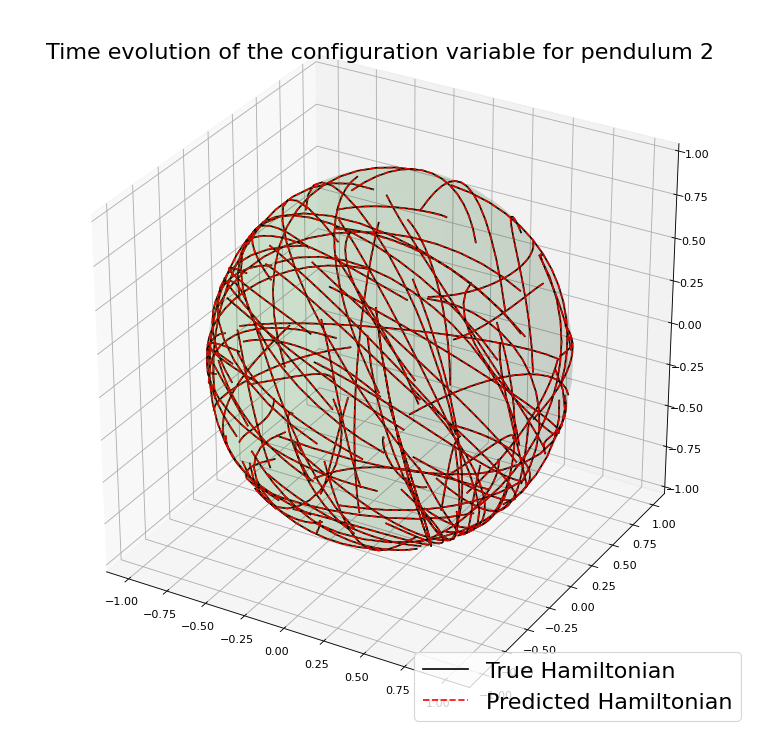
Example with \(\mathcal{Q}=S^2\)

\mathcal{Q}=\{q\in\mathbb{R}^3:\;\|q\|^2-1=0\}\subset\mathbb{R}^3,\\ dim\mathcal{Q}=2

P(q) : \mathbb{R}^3\rightarrow T_q\mathcal{Q},\,v\mapsto (I_3-qq^T)v

T_q\mathcal{Q} = \{v\in\mathbb{R}^3:\,q^Tv=0\}

\begin{cases} \dot{q} &=\left(I-q q^{T}\right) \partial_{p} H(q, p) \\ \dot{p} &=-\left(I-q q^{T}\right) \partial_{q} H(q, p)+\partial_{p} H(q, p) \times(p \times q) \end{cases}

On \(\mathcal{M}\) the dynamics can be written as

Using an integrator \(\Psi^{\Delta t}_{\theta}\) that preserves \(\mathcal{M}\)

PROS

CONS

On \(\mathcal{M}\) the function \(H_{\theta}\) is unique

The approximation error is not influenced by the drift from the manifold.

These methods are more involved, and often implicit.

The loss function can become harder to be optimized.

The simulated trajectories in the training are physically meaningful.

Not in general clear the impact this has on the final result.

Case with \(\mathcal{M}\) homogeneous

A manifold \(\mathcal{M}\) is homogeneous if there is a Lie group \(\mathcal{G}\) that defines a transitive group action \(\varphi:\mathcal{G}\times\mathcal{M}\rightarrow\mathcal{M}\).

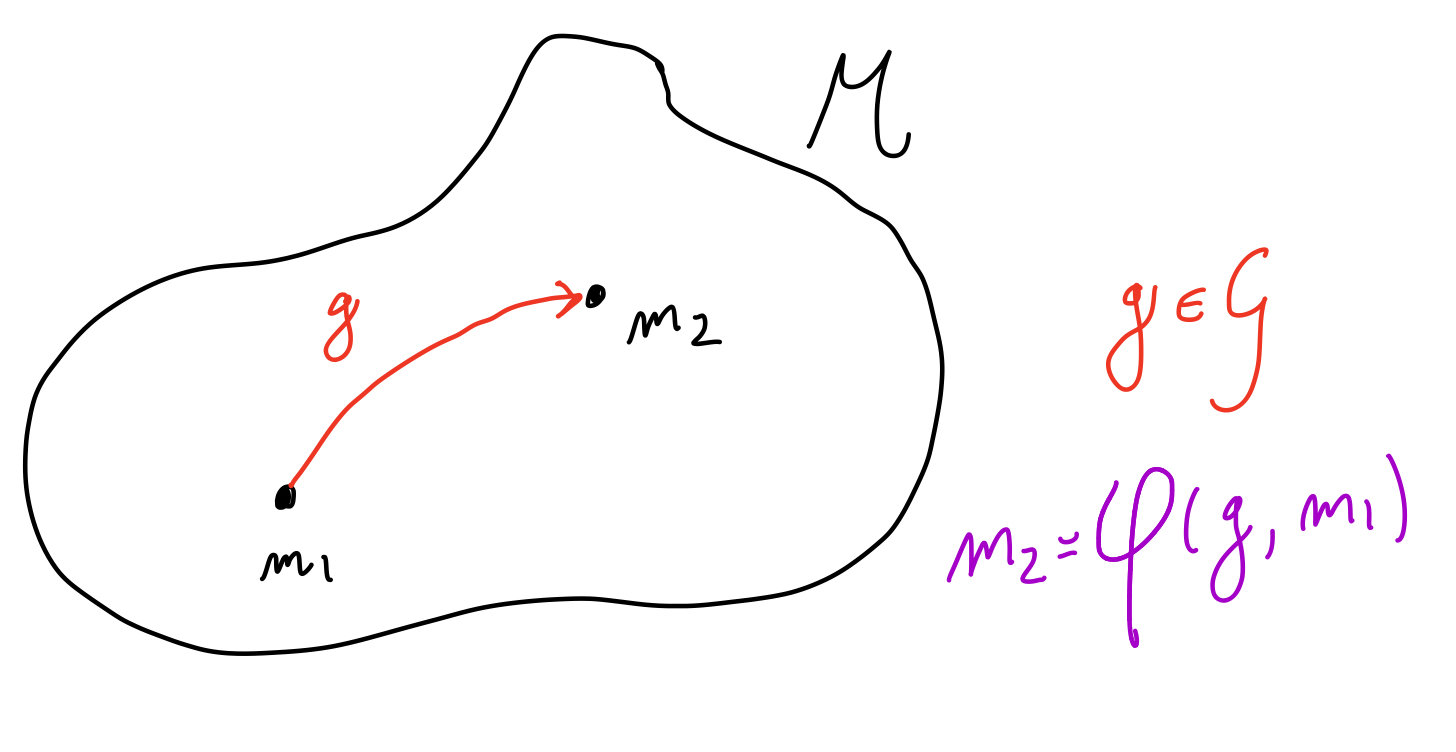
Case with \(\mathcal{M}\) homogeneous

A manifold \(\mathcal{M}\) is homogeneous if there is a Lie group \(\mathcal{G}\) that defines a transitive group action \(\varphi:\mathcal{G}\times\mathcal{M}\rightarrow\mathcal{M}\).

A vector field \(f\) on \(\mathcal{M}\) can be represented as \(f(x) = \varphi_*(\xi(x))(x)\), for a function

\(\xi:\mathcal{M}\rightarrow\mathfrak{g}\simeq T_e\mathcal{G}\).

Lie Group Methods are a class of methods exploiting this structure and preserving \(\mathcal{M}\). The simplest is Lie Euler:

\(y_i^{j+1} = \varphi(\exp(\Delta t \,\xi(y_i^j)),y_i^j)\)

Basic idea of a class of Lie group methods

\(\mathcal{M}\)

\(y_i^j\)

\(y_i^{j+1}=\varphi_g(y_i^j)\)

\(\mathfrak{g}\)

\(\xi\)

\(\exp\)

\(\mathcal{G}\)

\(\varphi_g\)

\(\Psi^{\Delta t}\)

\(0\)

\(\Delta t \xi(y_i^j)\)

\(g=\exp(\Delta t\,\xi(y_i^j))\)

\(f\in\mathfrak{X}(M)\)

\(f^L\in\mathfrak{X}(\mathfrak{g})\)