Structure preserving neural networks coming from ODE models

Davide Murari

SciCADE 2021 - 28/07/2022

\(\texttt{davide.murari@ntnu.no}\)

Joint work with Elena Celledoni, Brynjulf Owren,

Carola-Bibiane Schönlieb and Ferdia Sherry

What are neural networks

They are compositions of parametric functions

\( \mathcal{N}(x) = f_{\theta_k}\circ ... \circ f_{\theta_1}(x)\)

Example

\(f_{\theta}(x) = x + B\Sigma(Ax+b),\quad \theta = (A,B,b)\)

\(\Sigma(z) = [\sigma(z_1),...,\sigma(z_n)],\quad \sigma:\mathbb{R}\rightarrow\mathbb{R}\)

Neural networks modelled by dynamical systems

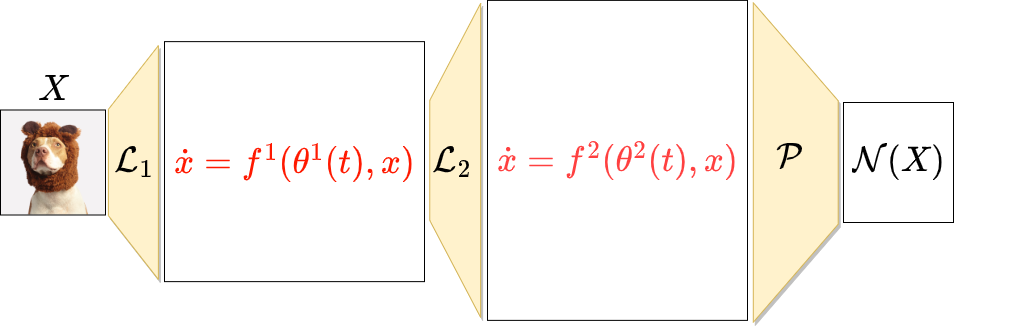
DYNAMICAL BLOCKS

Dynamical blocks

\mathcal{B}(x) = \Psi_{f_k}^{h_k}\circ ...\circ \Psi_{f_1}^{h_1}(x)

EXPLICIT

EULER

\( \Psi_{f_i}^{h_i}(x) = x + h_i f_i(x)\)

\( \dot{x}(t) = f(x(t),\theta(t)) \)

Time discretization : \(0 = t_1 < ... < t_k <t_{k+1}= T \), \(h_i = t_{i+1}-t_{i}\)

Where \(f_i(x) = f(x,\theta(t_i))\)

EXAMPLE

Imposing some structure

\dot{x}(t) = \left[\mathcal{M}(\theta(t),x(t))-\mathcal{M}^T(\theta(t),x(t))\right]\boldsymbol{1}
\dot{x}(t) = \mathbb{J}A^T(t)\Sigma(A(t)x(t)+b(t))
\ddot{x}(t) = \Sigma(A(t)x(t)+b(t))

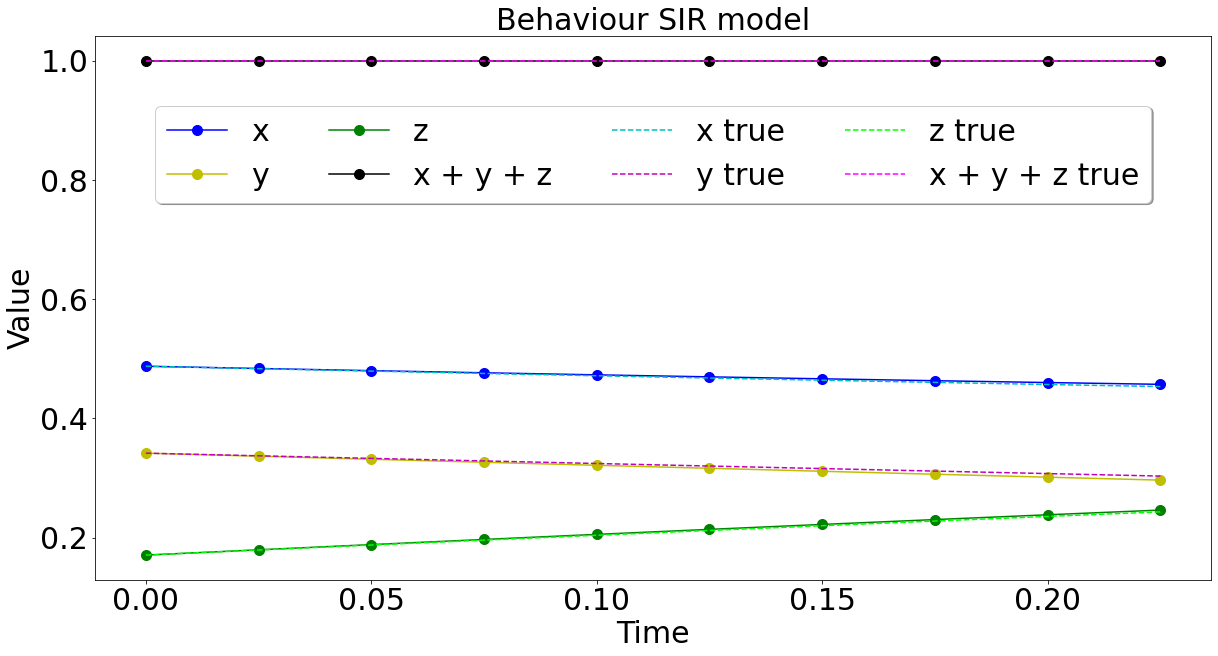
MASS PRESERVING DYNAMICAL BLOCKS

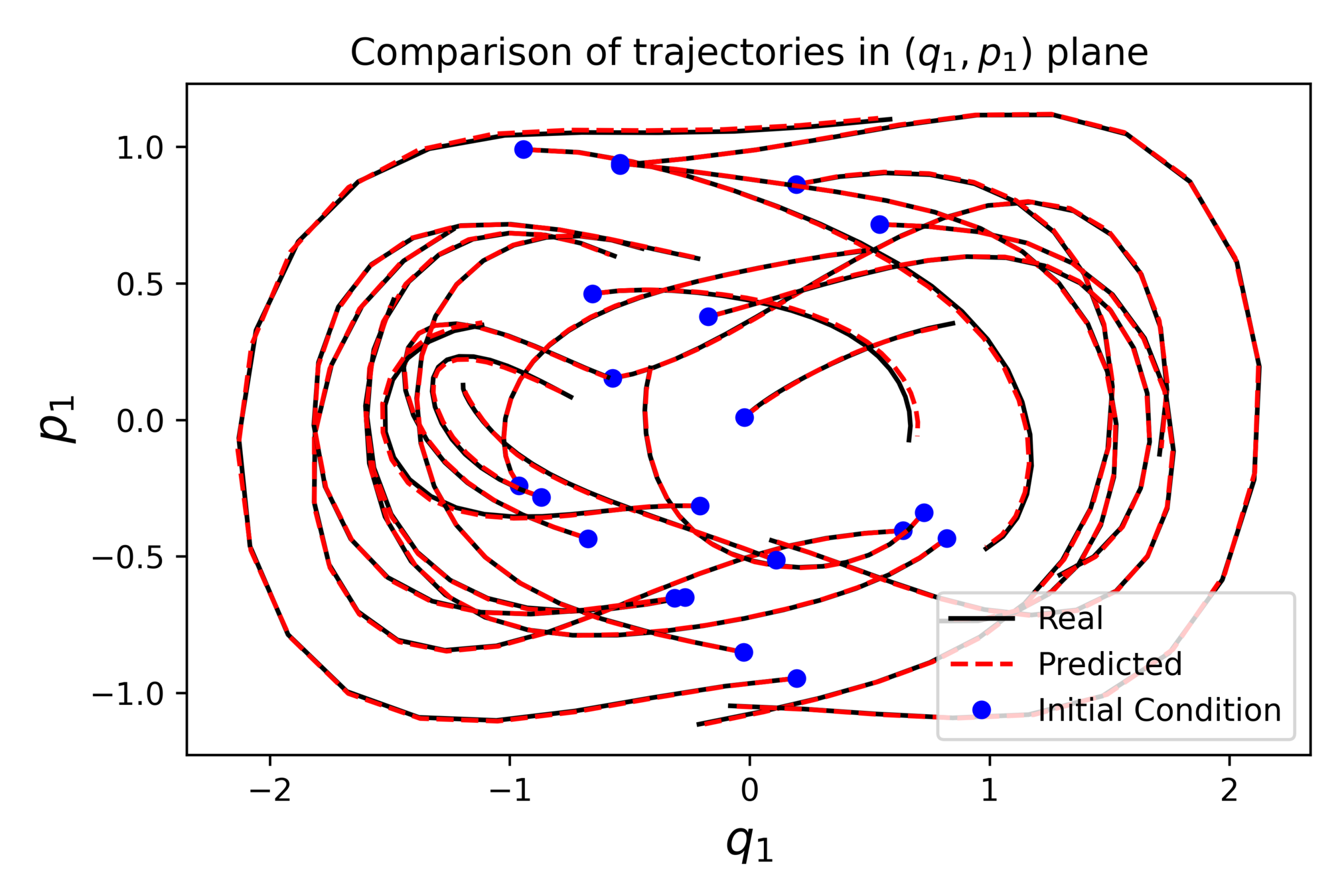
SYMPLECTIC DYNAMICAL BLOCKS

VOLUME PRESERVING DYNAMICAL BLOCKS

f_i = \nabla U_i + X_S^i
U_i(x) = \int_0^1 x^Tf_i(tx)dt
x^TX_S^i(x)=0\quad \forall x\in\mathbb{R}^n

Then \(F\) can be approximated with flow maps of gradient and sphere preserving vector fields.

F:\Omega\subset\mathbb{R}^n\rightarrow\mathbb{R}^n\quad \text{continuous, and}
\forall \varepsilon>0\,\,\exist f_1,…,f_k\in\mathcal{C}^1(\mathbb{R}^n,\mathbb{R}^n)\,\,\text{s.t.}
\|F-\Phi_{f_k}^{h_k}\circ … \circ \Phi_{f_1}^{h_1}\|<\varepsilon.

Can we still accurately approximate functions?

\Phi_{f_i}^h = \Phi_{f_i}^{\alpha_M h} \circ ... \circ \Phi_{f_i}^{\alpha_1 h}
\sum_{i=1}^M \alpha_i = 1
f = \nabla U + X_S \\ \implies \Phi_f^h = \Phi_{\nabla U}^{h/2} \circ \Phi_{X_S}^h \circ \Phi_{\nabla U}^{h/2} + \mathcal{O}(h^3)

1-Lipschitz neural networks and the classification problem

Description of the problem

Given a "sufficiently large" set of \(N\) points in \(\mathcal{M}\subset\mathbb{R}^k\) that belong to \(C\) classes, we want to learn a function \(F\) assigning all the points of \(\mathcal{M}\) to the correct class.

F : \mathbb{R}^k \rightarrow \mathbb{R}^C
\ell_F(x):=\arg\max\{F(x)_j:j=1,...,C\} = i=:\ell(x) \\ \forall x\in \mathcal{M}_i
\mathcal{M} = \bigcup\limits_{i=1}^C \mathcal{M}_i \subset \mathbb{R}^k

Adversarial examples

\text{Find }\eta\in\mathbb{R}^k\\ \text{s.t.}\,\,\|\eta\|\leq \varepsilon,\,\,\ell_F(x)\neq \ell_F(x+\eta)

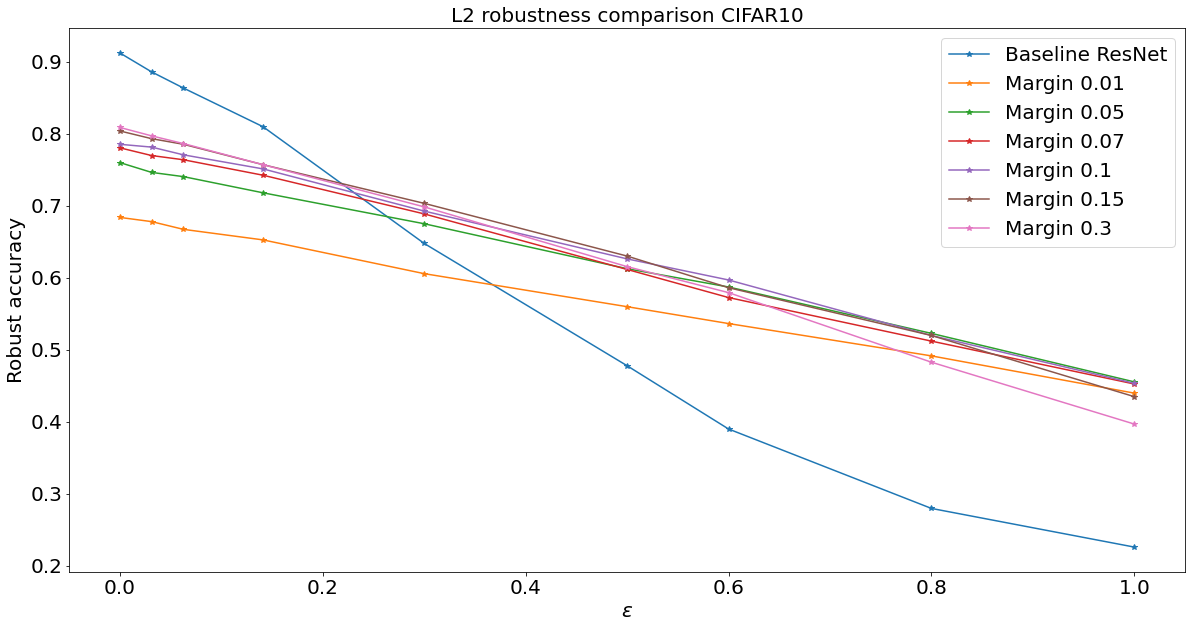
How to have guaranteed robustness

M_F(x) := \max\{0,F(x)_{i} - \max_{j\neq i} F(x)_j\}\\ \ell(x)=i\\ M_F(x)\geq \sqrt{2}\mathrm{Lip}(F)\varepsilon \\ \implies \ell_F(x) = \ell_F(x+\eta)\,\forall \|\eta\|\leq \varepsilon

We constrain the Lipschitz constant of \(F\)

Lipschitz dynamical blocks

X_{\theta}(x) := - \nabla V_{\theta}(x) = -A^T\Sigma(Ax+b)
\|\Phi^{t}_{X_{\theta}}(x)-\Phi^{t}_{X_{\theta}}(y)\|\leq e^{-\mu_{\theta} t} \|x-y\|
Y_{\theta}(x) := \Sigma(Wx + v),\quad \theta = [W,v]
\|\Phi^{t}_{Y_{\theta}}(x)-\Phi^{t}_{Y_{\theta}}(y)\|\leq e^{\ell_{\theta} t} \|x-y\|

Lipschitz dynamical blocks

\mathcal{B}_{\theta}(x)=\Phi_{X_{\theta_{2k}}}^{h_{2k}} \circ \Phi_{Y_{\theta_{2k-1}}}^{h_{2k-1}} \circ ... \circ \Phi_{X_{\theta_2}}^{h_2} \circ \Phi_{Y_{\theta_{1}}}^{h_1}(x)
\gamma_i = h_{2i-1}\ell_{\theta_{2i-1}} - h_{2i}\mu_{\theta_{2i}}

 We impose : \(\gamma_i\leq 0\)

\|\mathcal{B}_{\theta}(x)-\mathcal{B}_{\theta}(y)\|\leq \exp\left(\sum_{i=1}^k \gamma_i\right)\|x-y\|
\exp\left(\sum_{i=1}^k \gamma_i\right)

Adversarial robustness

Thank you for the attention

In progress:

Celledoni, E., Murari, D., Owren, B., Schönlieb, C. B., & Sherry, F.

Dynamical systems' based neural networks

Made with Slides.com