Talk ALUMNI

Some connections between dynamical systems and neural networks

Davide Murari

Veronesi Tutti Math Seminar - 06/04/2022

\(\texttt{davide.murari@ntnu.no}\)

What is supervised learning

Consider two sets \(\mathcal{C}\) and \(\mathcal{D}\) and suppose to be interested in a specific (unknown) mapping \(F:\mathcal{C}\rightarrow \mathcal{D}\).

The data we have available can be of two types:

Direct measurements of \(F\): \(\mathcal{T} = \{(x_i,y_i=F(x_i)\}_{i=1,...,N}\subset\mathcal{C}\times\mathcal{D}\)
Indirect measurements that characterize \(F\): \(\mathcal{I} = \{(x_i,z_i=G(F(x_i))\}_{i=1,...,N}\subset\mathcal{C}\times G(\mathcal{D})\)

GOAL: Approximate \(F\) on all \(\mathcal{C}\).

Examples of these tasks

What are neural networks

Source image: https://www.tibco.com/reference-center/what-is-a-neural-network

What are neural networks

They are compositions of parametric functions

\( \mathcal{NN}(x) = f_{\theta_k}\circ ... \circ f_{\theta_1}(x)\)

Examples

\(f_{\theta}(x) = x + B\Sigma(Ax+b),\quad \theta = (A,B,b)\)

ResNets

Feed Forward

Networks

\(f_{\theta}(x) = B\Sigma(Ax+b),\quad \theta = (A,B,b)\)

\(\Sigma(z) = [\sigma(z_1),...,\sigma(z_n)],\quad \sigma:\mathbb{R}\rightarrow\mathbb{R}\)

Neural networks motivated by dynamical systems

\mathcal{NN}(x) = \Phi_{f_k}^{h_k}\circ ...\circ \Phi_{f_1}^{h_1}(x)

EXPLICIT

EULER

\( \Phi_{f_i}^{h_i}(x) = x + h_i f_i(x)\)

\( \dot{x}(t) = f(t,x(t),\theta(t)) \)

Time discretization : \(0 = t_1 < ... < t_k <t_{k+1}= T \), \(h_i = t_{i+1}-t_{i}\)

Where \(f_i(x) = f(t_i,x,\theta(t_i))\)

EXAMPLE

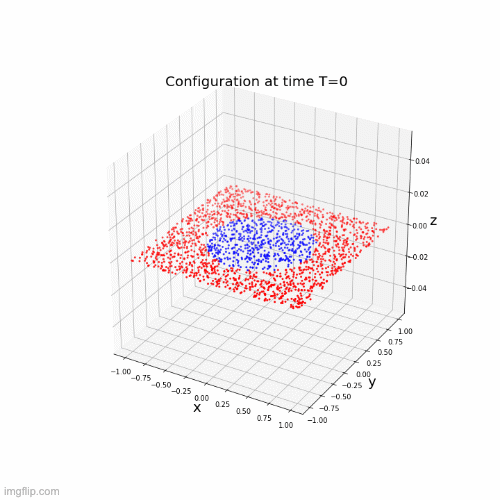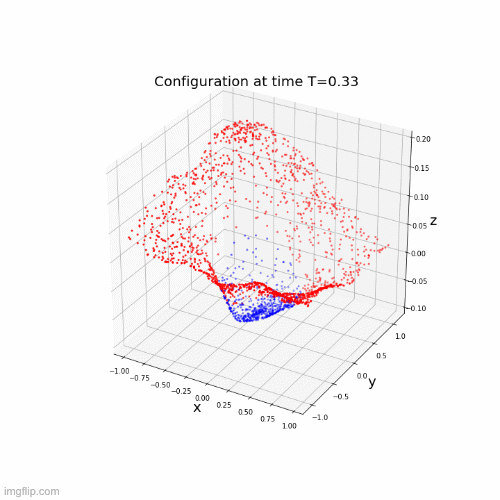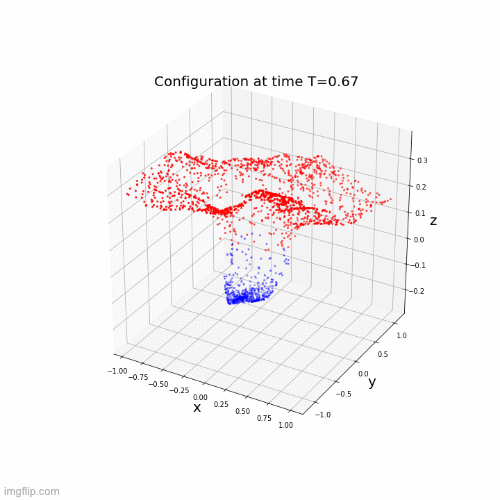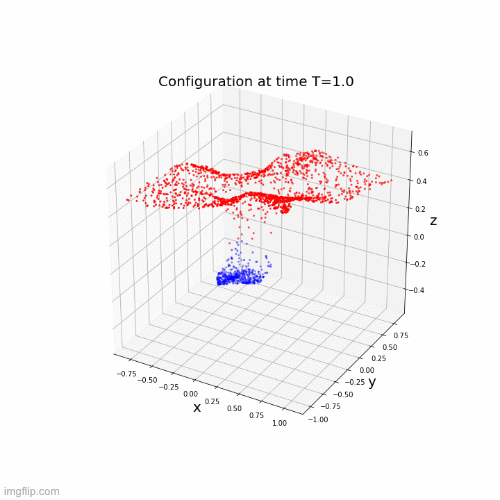
\(\dot{x}(t) = \Sigma(A(t)x(t) + b(t))\)

Imposing some structure

\dot{x}(t) = -A^T(t)\Sigma(A(t)x(t) + b(t)) =\\ -\nabla \left( \boldsymbol{1}^T\Gamma(A(t)x(t)+b(t)) \right)

\dot{x}(t) = \mathbb{J}A^T(t)\Sigma(A(t)x(t)+b(t))

\ddot{x}(t) = \Sigma(A(t)x(t)+b(t))

1-LIPSCHITZ NETWORKS

HAMILTONIAN NETWORKS

VOLUME PRESERVING, INVERTIBLE

Hamiltonian systems

\mathbb{J} = \begin{bmatrix} 0_n & I_n \\ -I_n & 0_n \end{bmatrix}\in\mathbb{R}^{2n\times 2n}

X_H(x) = \mathbb{J}\nabla H(x),\quad H:\mathbb{R}^{2n}\rightarrow\mathbb{R}

\mathcal{L}_{X_H} H(x) = \nabla H(x)^T\mathbb{J}\nabla H(x) = 0

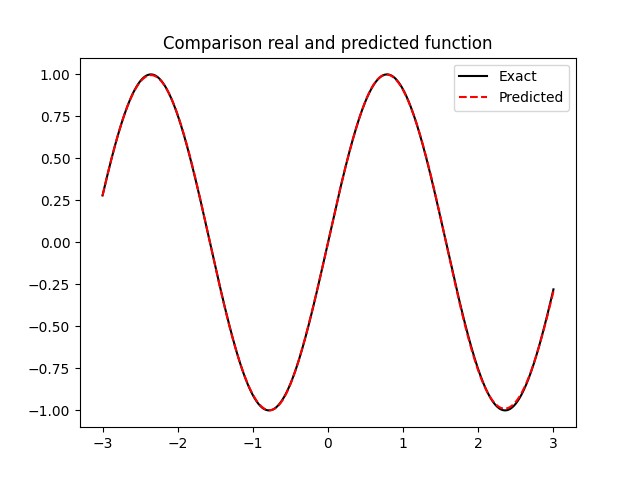
Approximating Hamiltonian systems with neural networks

GOAL: Approximate a Hamiltonian vector field \(X_H\in\mathfrak{X}(\mathbb{R}^{2n})\)

DATA: \(\mathcal{T} = \{(x_i,y_i^1,...,y_i^M)\}_{i=1,...,N}\)

\(y_i^j = \phi_{X_H}^{jh}(x_i) + \delta_i^j \)

\mathcal{NN}_{\Theta}(q,p) = \frac{1}{2}p^T A^T A p + f_{\theta_k} \circ ..\circ f_{\theta_1}(q)

KINETIC

ENERGY

POTENTIAL

ENERGY

\(\Theta=(\theta_1,...,\theta_k,A)\)

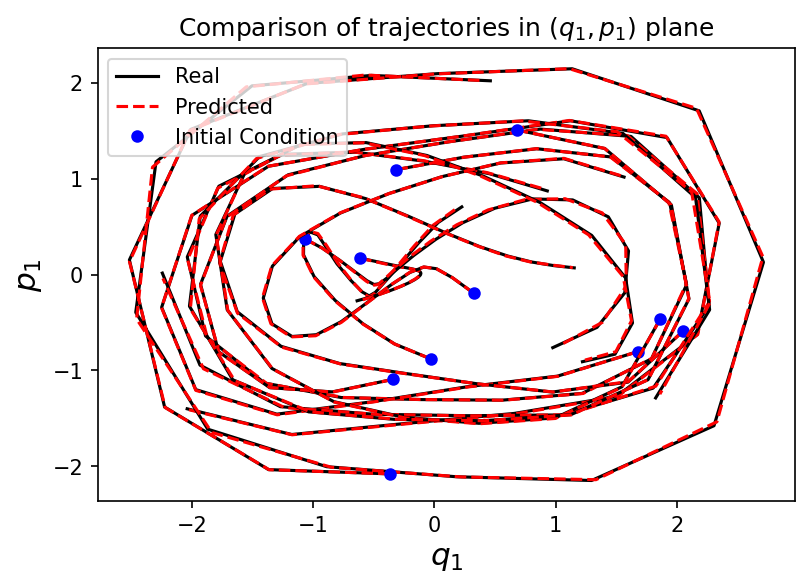
Approximating Hamiltonian systems with neural networks

\( Y_{\Theta}(q,p) = X_{\mathcal{NN}_{\Theta}}(q,p) = \mathbb{J}\nabla \mathcal{NN}_{\Theta}(q,p) \)

\( \Phi^h_{Y_{\Theta}} \) a one-step numerical method for \(Y_{\Theta}\)

Training:

\(\hat{y}_i^1 = \Phi_{Y_{\Theta}}^h(x_i)\)

\(\hat{y}_i^{j+1} = \Phi_{Y_{\Theta}}^h(\hat{y}_i^j)\)

\min_{\Theta} \frac{1}{N} \sum_{i=1}^N \sum_{j=1}^M \left\|y_i^j - \hat{y}_i^j\right\|^2

Thank you for the attention