Robustness of neural networks for classification problems
Davide Murari
MaGIC 2022 - 02/03/2022
Part of a joint project together with Elena Celledoni, Brynjulf Owren,
Carola-Bibiane Schönlieb and Ferdia Sherry


The classification problem
Given a "sufficiently large" set of \(N\) points in \(\mathcal{M}\subset\mathbb{R}^k\) that belong to \(C\) classes, we want to learn a function \(F\) assigning all the points of \(\mathcal{M}\) to the correct class.
Adversarial examples

What is a robust classifier?
An \(\varepsilon\)-robust classifier is a function that not only correctly classifies the points in \(\mathcal{M}\) but also those in
Suppose that
What is a robust classifier?
An \(\varepsilon\)-robust classifier is a function that not only correctly classifies the points in \(\mathcal{M}\) but also those in
Suppose that
1.
2.
In other words, we should learn a
such that

The choice of the Euclidean metric
From now on, we denote with \(\|\cdot\|\) the \(\ell^2\) norm.
The sensitivity to input perturbations
The Lipschitz constant of \(F\) can be seen as a measure of its sensitivity to input perturbations:
Lipschitz networks based on dynamical systems
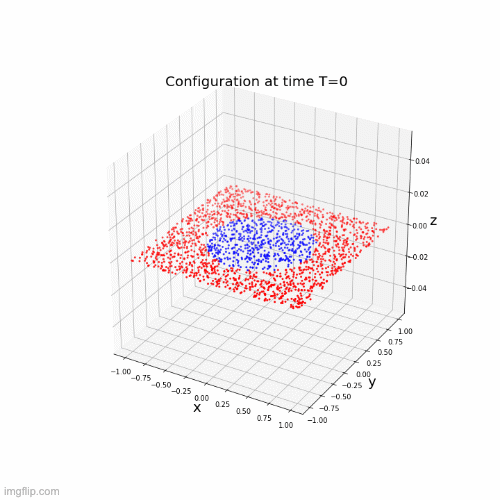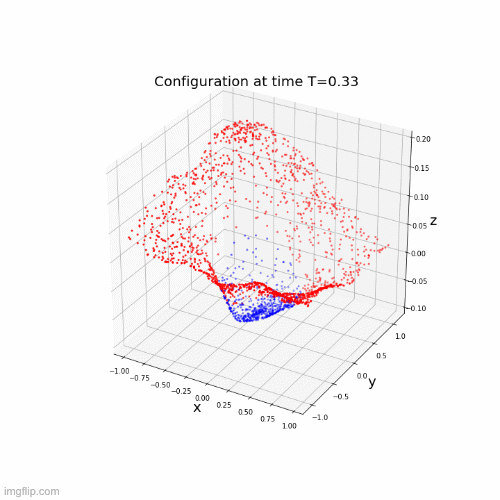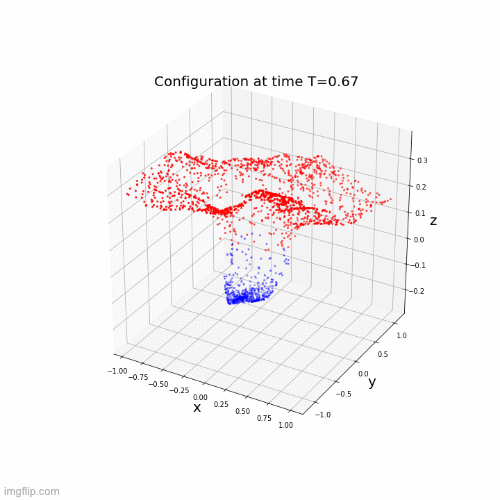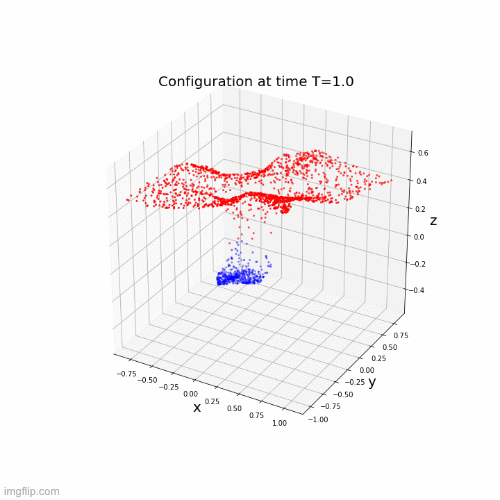
Lipschitz networks based on dynamical systems
piecewise constant
The notion of margin
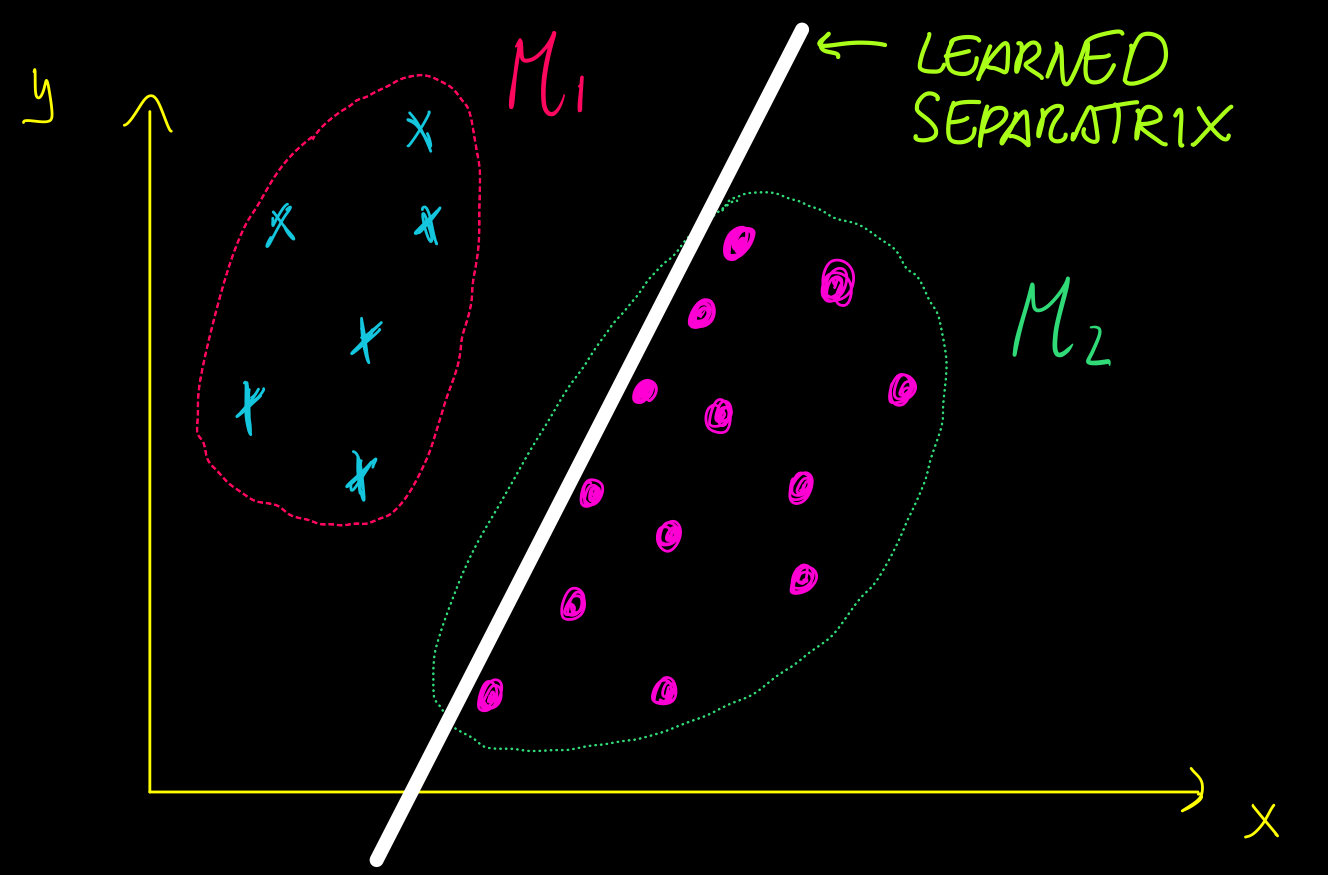
It is not enough to have a small Lipschitz constant.
Idea:
"GOOD"
"BAD"
The classifier might have a small Lipschitz constant but be very sensitive to input perturbations.
The notion of margin

It is not enough to have a small Lipschitz constant.
Idea:
"GOOD"
"BAD"
LOSS
FUNCTION
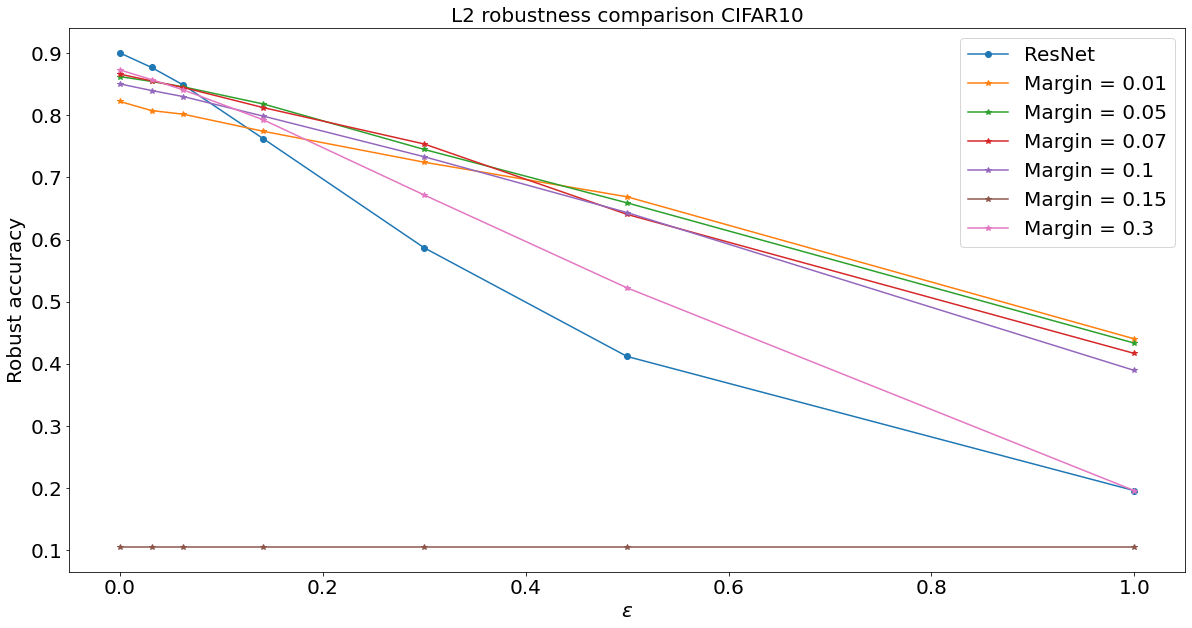
Experiments for \(\ell^2\) robust accuracy
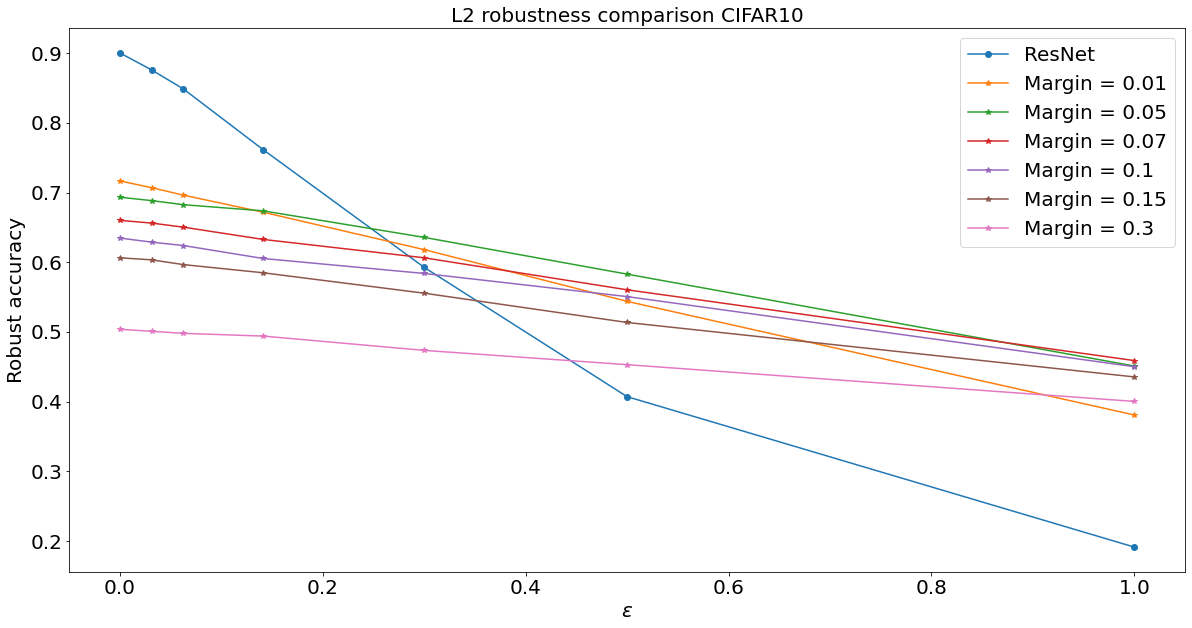
Experiments for \(\ell^2\) robust accuracy
Thank you for the attention