Predictions Based on

Pixel Data

Davide Murari

davide.murari@ntnu.no

In collaboration with : Elena Celledoni, James Jackaman, Brynjulf Owren

TES Conference on Mathematical Optimization for Machine Learning

Pixel-based learning

\(U_i^{n+1} = \Phi^{\delta t}(U_i^n)+\delta_i^j\)

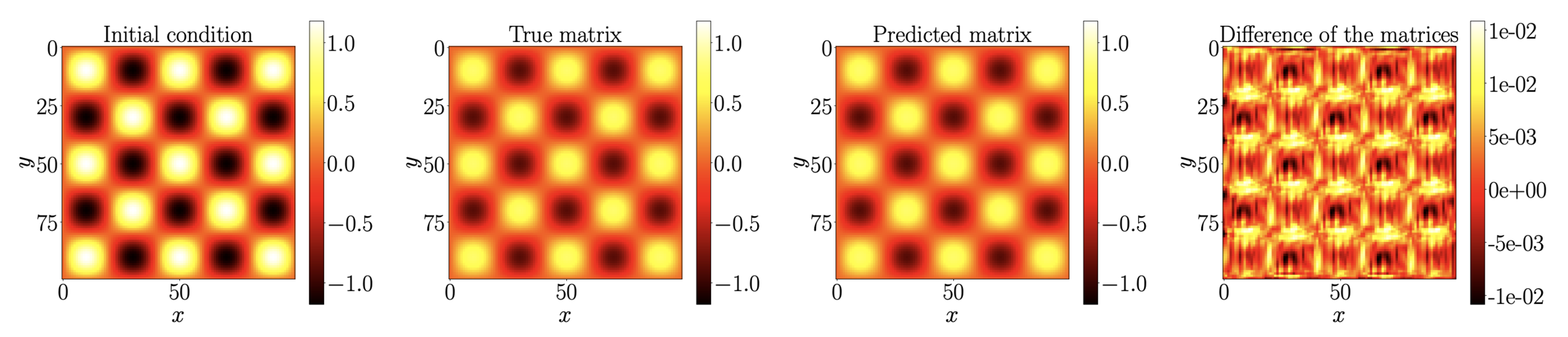
Predictions at time \(40\delta t\)

Fisher's equation:

\(\partial_t u=\alpha \Delta u+u(1-u)\)

DATA: \(\{(U_i^0,U_i^1,...,U_i^M\}_{i=1,...,N}\)

Definition of the goal

\(\mathcal{F}\)

\(\mathcal{C}^0\)

\(\Phi^{\delta t}\)

\(f_{\theta}\)

Given 2-layer convolutional neural networks, defining the space \(\mathcal{F}\), we want to see how well \(\Phi^{\delta t}\) can be approximated by functions in \(\mathcal{F}\).

Is there a constructive way to realize that approximation?

Approximation of space-time dynamics of PDEs

{

\delta x

\partial_t u = \mathcal{L}u + \sum_{i=1}^n\beta_i\,(\partial_{\alpha_{i1}}u)\, (\partial_{\alpha_{i2}}u),\\ \beta_i\in\mathbb{R},\,\,\alpha_{ij}\in \mathbb{N}^2

u=u(t,x,y)\in\mathbb{R}

\(0=t_0 < t_1<...<t_M\)
\((U^n)_{rs} = u(t_n,x_r,y_s)\)

\(x_r=r\delta x,\,\,y_s=s\delta x\)

Method of lines

Initial PDE

\partial_t u = \mathcal{L}u + \sum_{i=1}^n\beta_i\,(\partial_{\alpha_{i1}}u)\, (\partial_{\alpha_{i2}}u)

Method of lines

Initial PDE

\partial_t u = \mathcal{L}u + \sum_{i=1}^n\beta_i\,(\partial_{\alpha_{i1}}u)\, (\partial_{\alpha_{i2}}u)

Method of lines

\dot{U}(t)=L * U(t)+\sum_{i=1}^n \beta_i \left(D_{i 1} * U(t)\right) \odot \left(D_{i 2} * U(t)\right) \\ =: F(U(t))

Initial PDE

Semidiscretisation in space with finite differences

(U(t))_{rs} \approx u(x_r,y_s,t)

\partial_t u = \mathcal{L}u + \sum_{i=1}^n\beta_i\,(\partial_{\alpha_{i1}}u)\, (\partial_{\alpha_{i2}}u)

Method of lines

\dot{U}(t)=L * U(t)+\sum_{i=1}^n \beta_i \left(D_{i 1} * U(t)\right) \odot \left(D_{i 2} * U(t)\right) \\ =: F(U(t))

U^{n+1} = U^n + \delta t F(U^n)=: \Psi_{F}^{\delta t}(U^n)

Initial PDE

Semidiscretisation in space with finite differences

Approximation of the time dynamics

(U(t))_{rs} \approx u(x_r,y_s,t)

\partial_t u = \mathcal{L}u + \sum_{i=1}^n\beta_i\,(\partial_{\alpha_{i1}}u)\, (\partial_{\alpha_{i2}}u)

Finite differences as convolutions

R = K*U

\frac{1}{\delta x^2}\left[\begin{array}{ccc} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{array}\right] * U=\Delta u\left(t, x_i, y_j\right)+\mathcal{O}\left(\delta x^2\right)

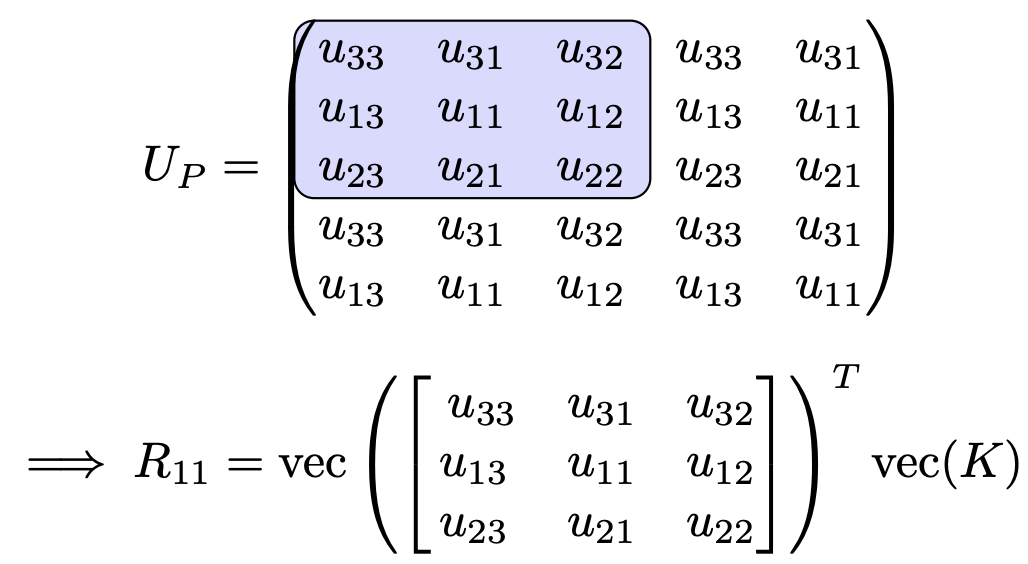
Example

Error splitting

\begin{aligned} & \left\|U^{n+1}-\Psi_{F_\theta}^{\delta t}\left(U^n\right)\right\| \\ & =\left\|\mathcal{O}\left(\delta x^2\right)+\Phi_F^{\delta t}\left(U^n\right)-\Psi_{F_\theta}^{\delta t}\left(U^n\right)\right\| \\ & \leq \mathcal{O}\left(\delta x^2\right)+\left\|\Phi_F^{\delta t}\left(U^n\right)-\Psi_F^{\delta t}\left(U^n\right)+\Psi_F^{\delta t}\left(U^n\right)-\Psi_{F_\theta}^{\delta t}\left(U^n\right)\right\| \\ & \leq \underbrace{\mathcal{O}\left(\delta x^2\right)}_{\text {spatial error }}+\underbrace{\left\|\Phi_F^{\delta t}\left(U^n\right)-\Psi_F^{\delta t}\left(U^n\right)\right\|}_{\text {classical error estimate }}+\underbrace{\left\|\Psi_F^{\delta t}\left(U^n\right)-\Psi_{F_\theta}^{\delta t}\left(U^n\right)\right\|}_{\text {neural network approximation }} \\ & \leq \mathcal{O}\left(\delta x^2\right) + \mathcal{O}\left(\delta t^{r+1}\right) + \left\|\Phi_F^{\delta t}\left(U^n\right)-\Phi_{F_\theta}^{\delta t}\left(U^n\right)\right\|\\ & \leq \mathcal{O}\left(\delta x^2\right) + \mathcal{O}\left(\delta t^{r+1}\right) + \delta t \exp (\operatorname{Lip}(F) \delta t) \sup _{\|U\| \leq c}\left\|F_\theta(U)-F(U)\right\| \end{aligned}

U^n \mapsto \Psi_{F_{\theta}}^{\delta t}(U^n)

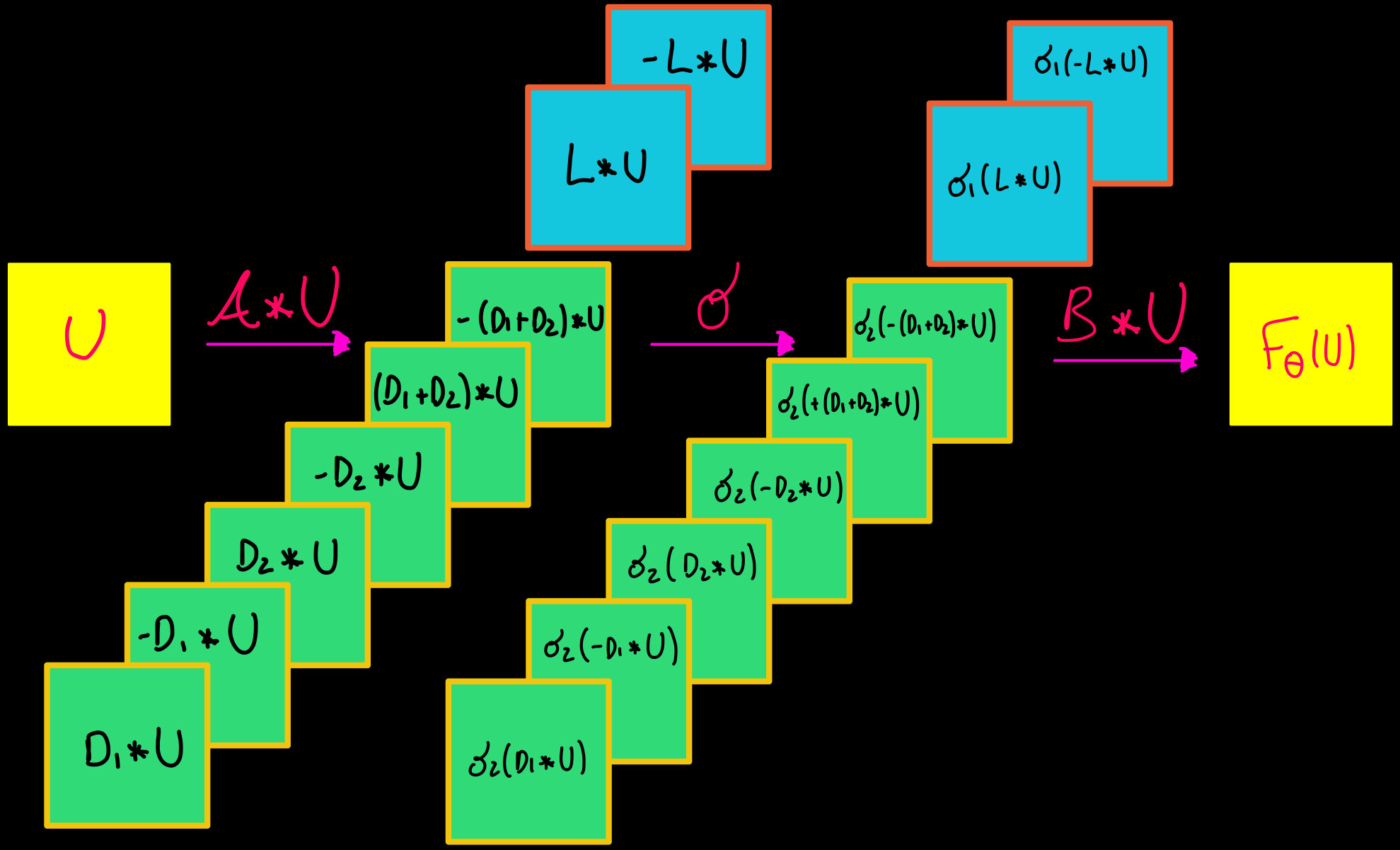
Layer of a ResNet we want to study

Splitting:

Useful activation functions

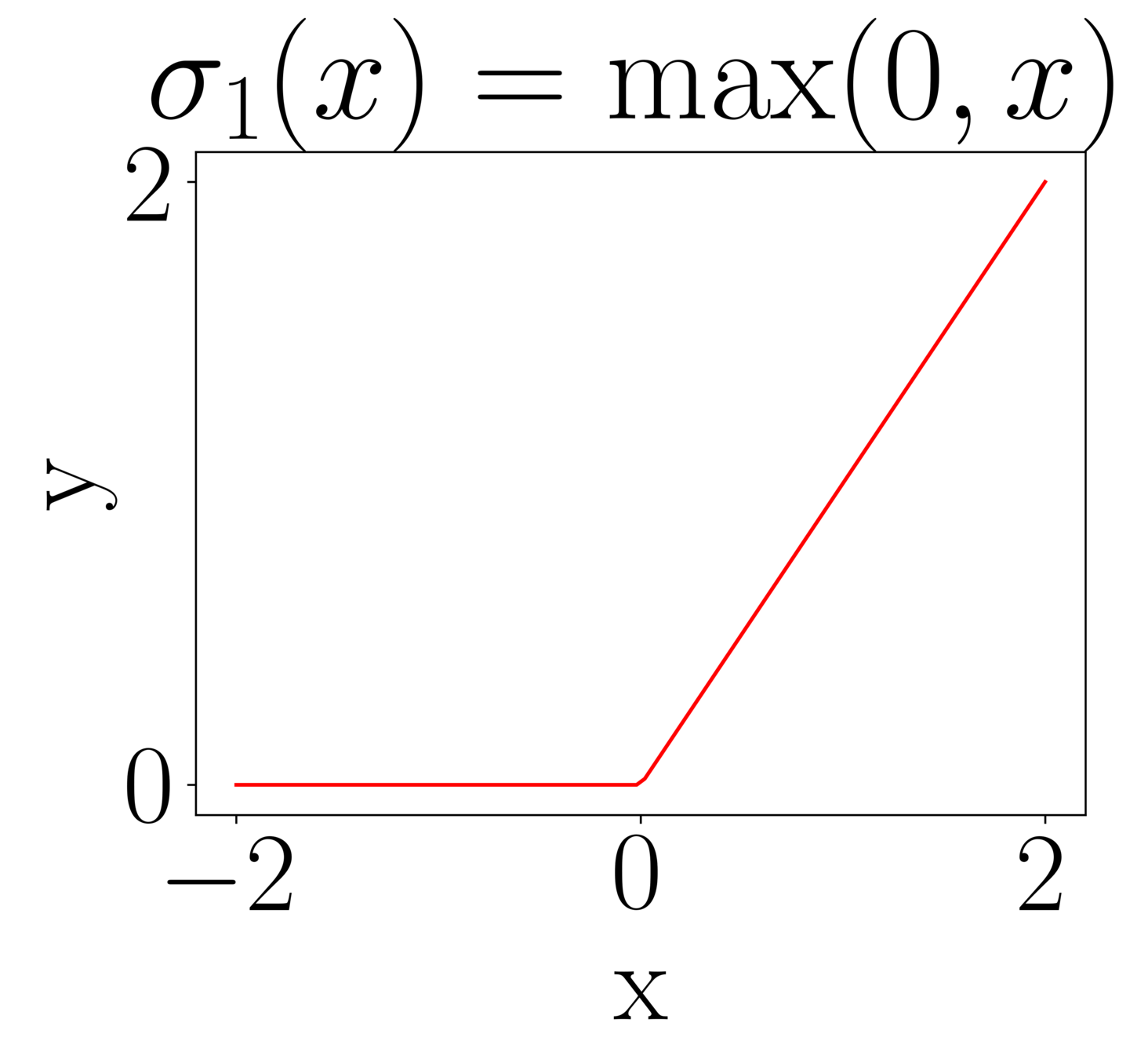
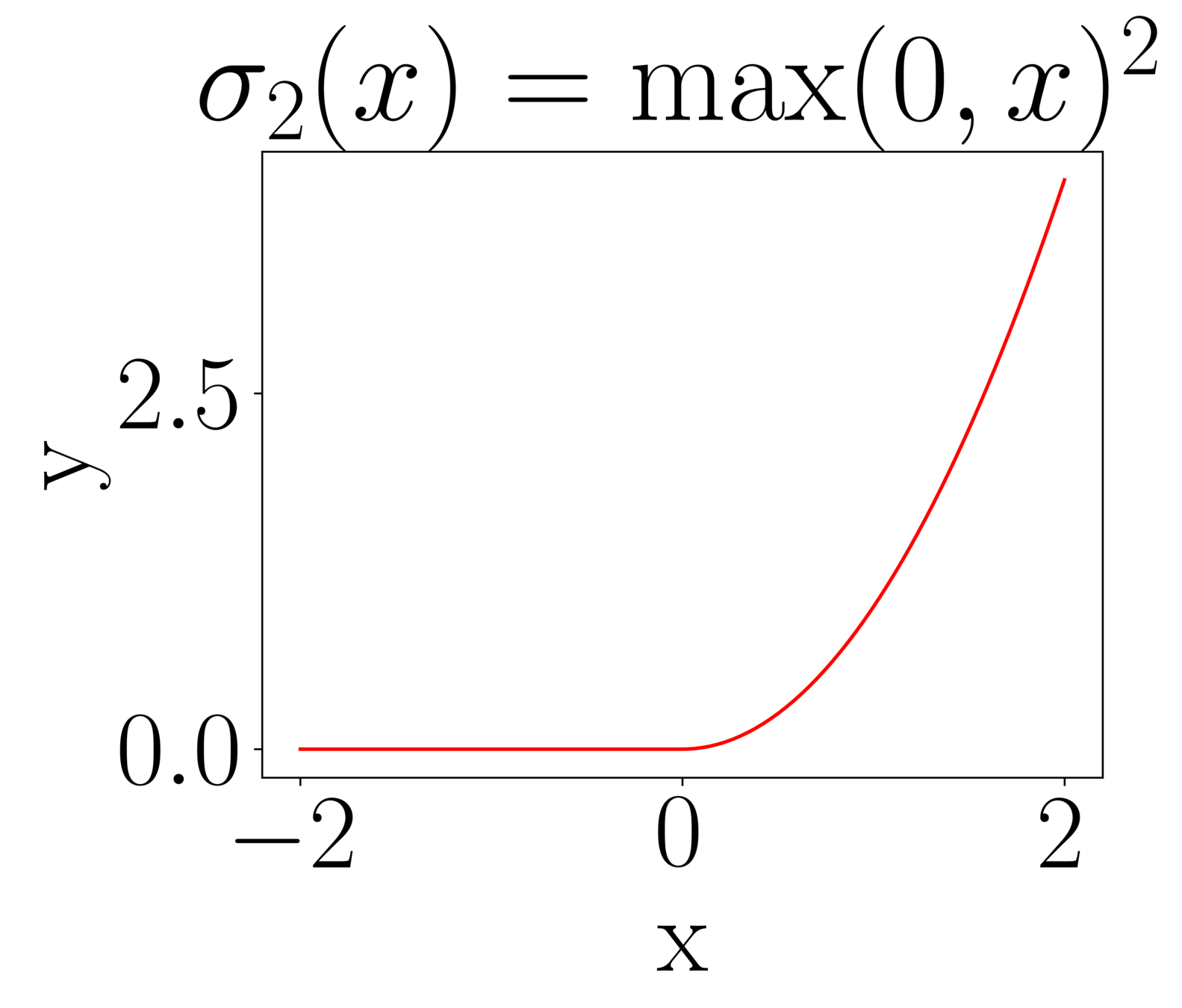
Simple but useful property:

\(x^p = \max(0,x)^p + (-1)^p\max(0,-x)^p\)

Approximation theorem

F(U) = L*U + (D_1*U) \odot (D_2*U)

Simplified setting

2ab = (a+b)^2 - (a^2 + b^2)\\ = \sigma_2(a+b) + \sigma_2(-(a+b))- \\ \left(\sigma_2(a) +\sigma_2(-a) + \sigma_2(b)+\sigma_2(-b) \right)

a = \sigma_1(a) - \sigma_1(a)

Approximation theorem

F_{\theta}(U) := \mathcal{\boldsymbol{B}} * \sigma(\mathcal{\boldsymbol{A}}*U)

Approximation theorem

F_{\theta}(U) := \mathcal{\boldsymbol{B}} * \sigma(\mathcal{\boldsymbol{A}}*U)

\begin{aligned} & \left\|U^{n+1}-\Psi_{F_\theta}^{\delta t}\left(U^n\right)\right\|\\ &\leq \mathcal{O}\left(\delta x^2\right) + \mathcal{O}\left(\delta t^{r+1}\right) + \delta t \exp (\operatorname{Lip}(F) \delta t) \sup _{\|U\| \leq c}\left\|F_\theta(U)-F(U)\right\| \end{aligned}

This can theoretically be 0. In practice, it depends on to the optimisation error.

This implies

\min_{G\in \mathcal{F}}\|U^{n+1} - \Psi^{\delta t}_{G}(U^n)\|\leq \mathcal{O}\left(\delta x^2\right) + \mathcal{O}\left(\delta t^{r+1}\right)

Thank you for the attention

Celledoni, E., Jackaman, J., M., D., & Owren, B., preprint (2023). Predictions Based on Pixel Data: Insights from PDEs and Finite Differences.