Metodo di studio per teoremi e dimostrazioni

Premessa:

Non esiste "il metodo perfetto" per studiare dimostrazioni matematiche. Possiamo migliorare come ci approcciamo a queste, ma rimarranno concetti difficili da capire e ricordare.

Cosa vuol dire studiare una dimostrazione?

Insieme delle ipotesi

Tesi

Provare a costruirla da soli

Siamo molto più bravi a ricordarci le cose che ci siamo sudati, su cui abbiamo lavorato parecchio. È molto più facile ricordare qualcosa che abbiamo costruito rispetto a qualcosa che abbiamo letto.

Enunciato : Un numero è divisibile per 9 se e soltanto se lo è la somma delle sue cifre.

a_0+a_1+...+a_k

n = 9\bar{n}

n = \sum_{j=0}^k a_j10^j

Dividere il procedimento in parti ben distinte

Obsidian

Una tecnica molto utile

per me

Caso generico

Esempio con \(n=936\)

n = 9\cdot10^2 + 3\cdot 10 + 6\\ n = 9(100-1+1) + 3(10-1+1) + 6\\ n = 9(99+1) + 3(9+1) + 6\\ n = 9(99) + 3(9) + (9+3+6)\\ n = 9(11\cdot 9) + 3(9\cdot 1) + (9+3+6)\\ n=9\bar{n}\iff 9+3+6=9\bar{k}\\ \bar{k}=2.

Dare un nome informativo alle parti e ricordarsi l'ordine

Ricostruire la dimostrazione partendo dai titoletti

Enunciato

Ipotesi

Espansione

Raccoglimento

Tesi

Aspettare...e provare a ricordare

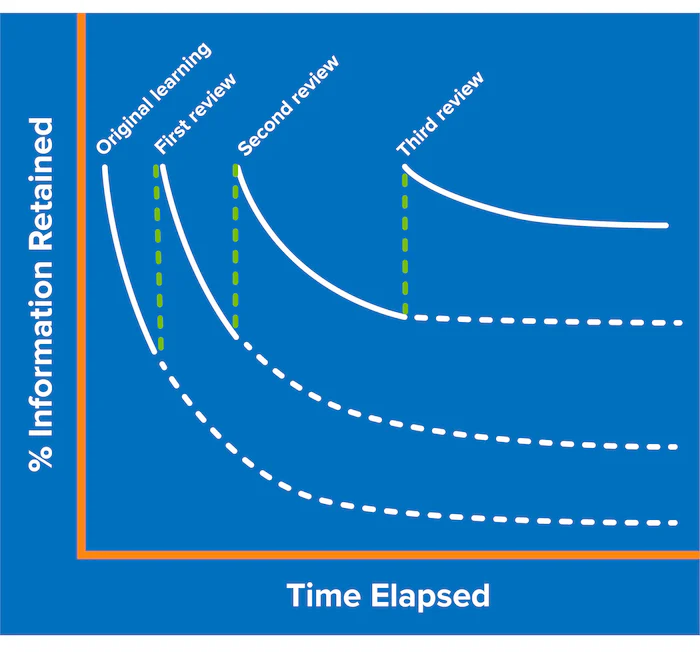
Un'app che potrebbe aiutare

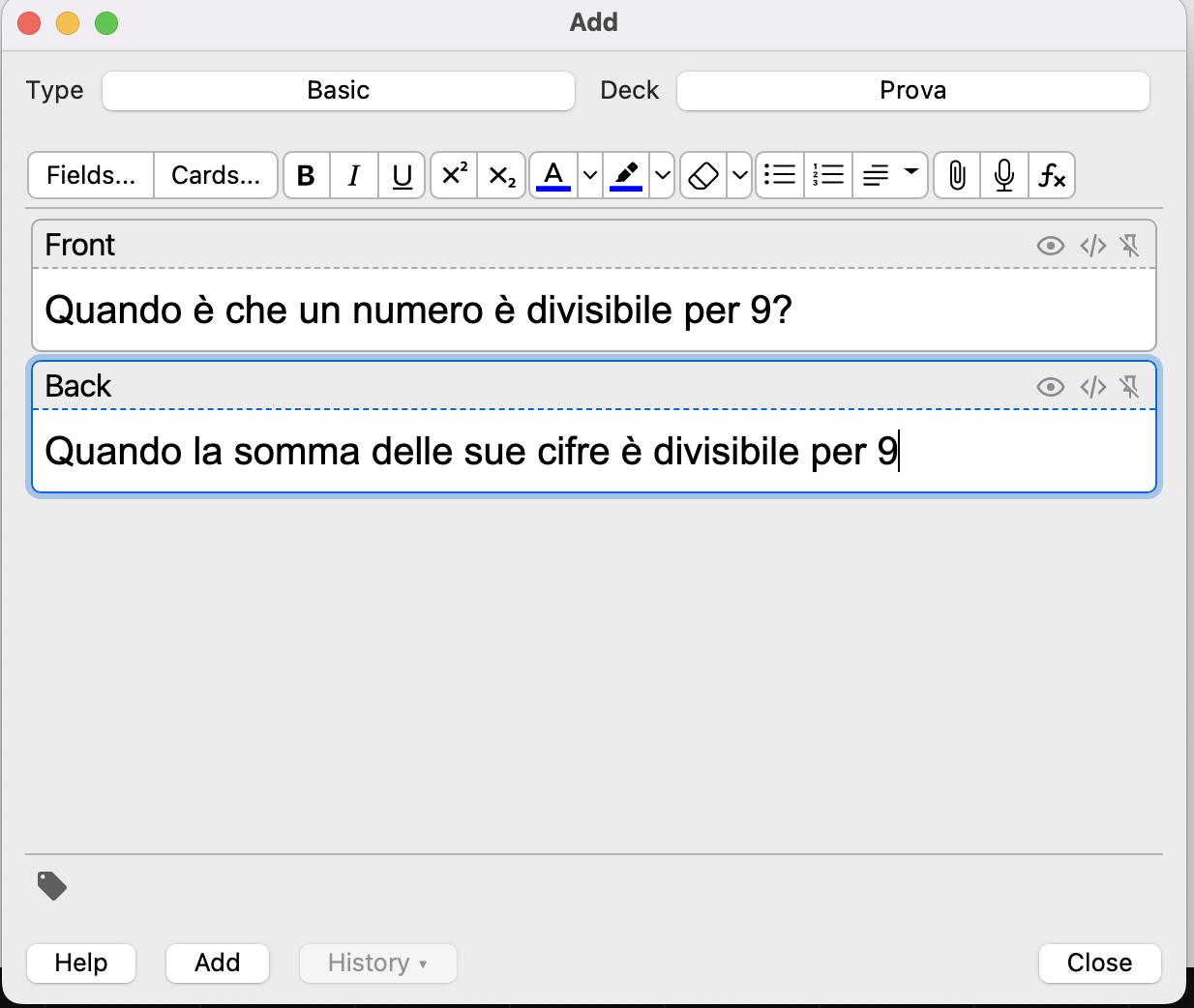
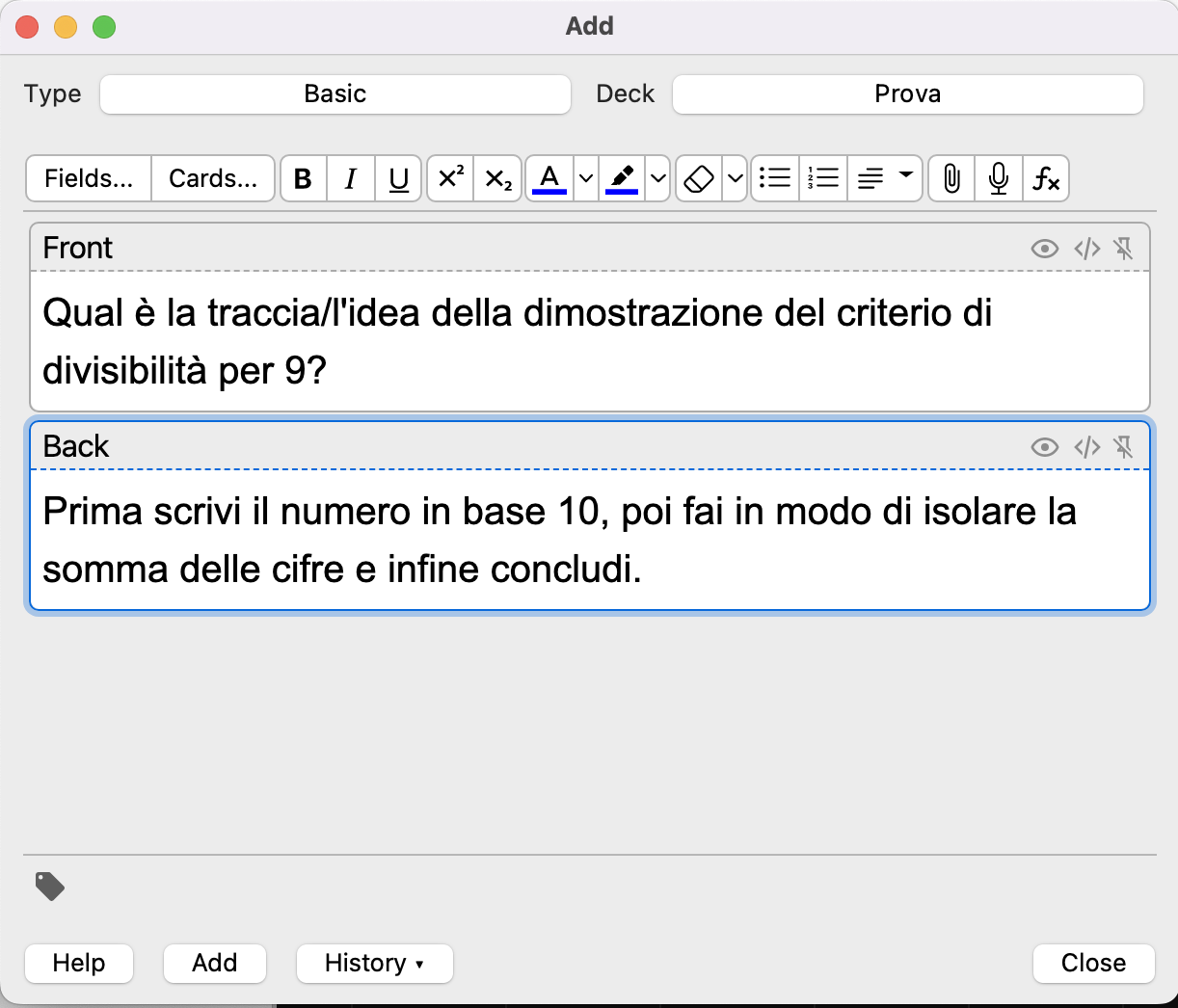
ANKI

Memorizzazione

La memoria non è molto affidabile e soprattutto se memorizziamo e basta rischiamo di ripartire da zero ogni volta.

Lo studio della matematica è incrementale, e più esempi abbiamo visto, più siamo anche in grado di creare nuova matematica e dimostrare nuovi risultati.

Ci sono però alcuni casi in cui un po' di memorizzazione è fondamentale a mio parere.

Memorizzazione

Esempio

Senza memorizzare questo punto di partenza, può risultare parecchio complicato ricostruire la dimostrazione.

Rappresentazione grafica

f(x+\gamma p) \approx f(x) + \gamma p^T\nabla f(x)< f(x)

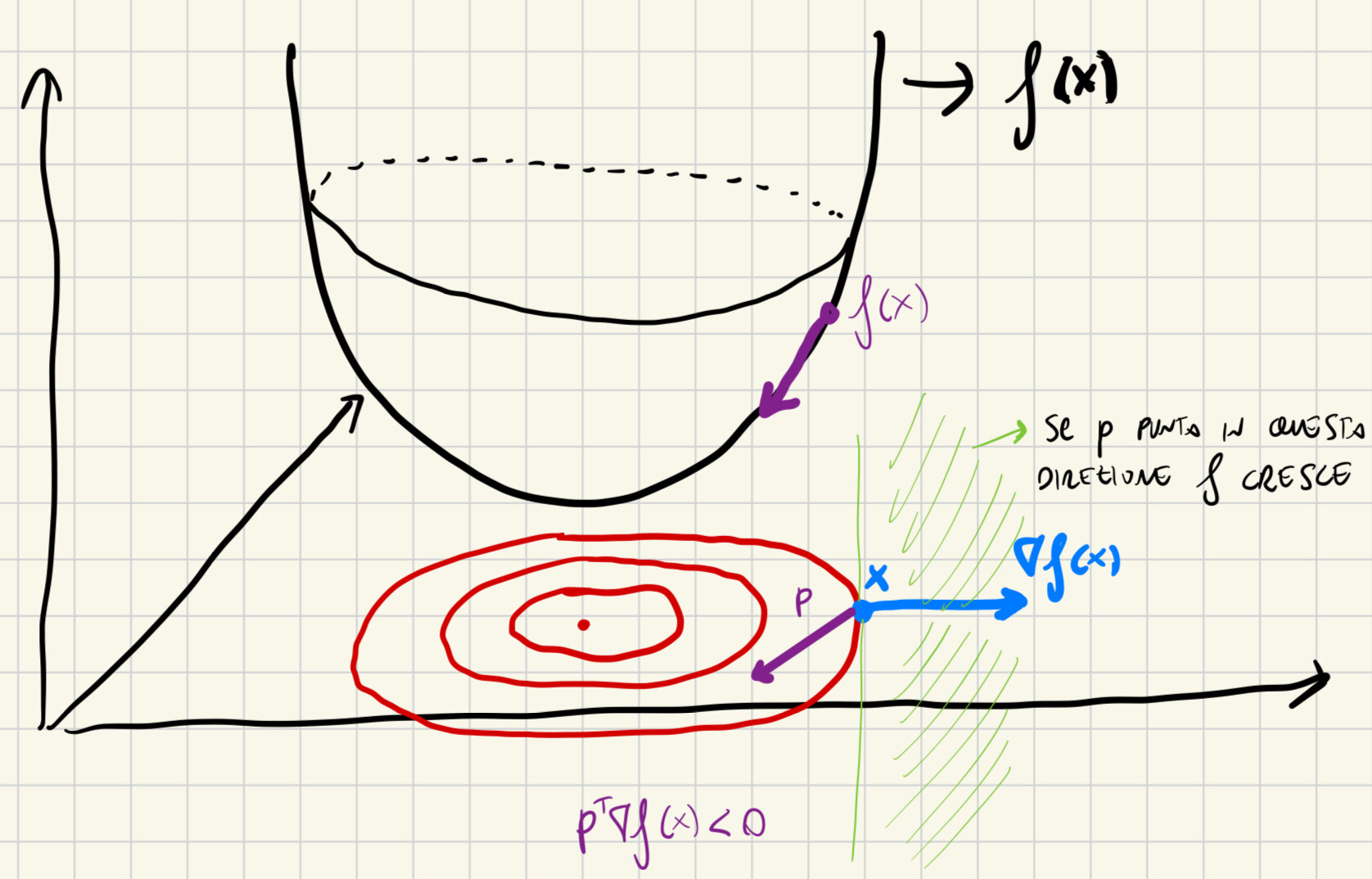
E se la dimostrazione è molto astratta?

Come fai ad immaginarti una sfera in dimensione 10?

Pensi ad una sfera in \(\mathbb{R}^3\) e ti ripeti tante volte che è 10-dimensionale

Non siamo bravi a lavorare con concetti troppo astratti. È quindi bene cercare sempre di lavorare con esempi, casi particolari ed analogie per capire i ragionamenti e concetti astratti.