From neural networks to dynamical systems and back

Davide Murari

Talk at CIA seminar - 24/03/2023

\(\texttt{davide.murari@ntnu.no}\)

In collaboration with : Elena Celledoni, Andrea Leone, Brynjulf Owren, Carola-Bibiane Schönlieb and Ferdia Sherry

Neural networks

Dynamical

systems

  • Approximating unknown vector fields
  • Approximating solutions of ODEs
  • Theoretical study of ResNets
  • Designing ResNets with desired properties

Supervised learning

Consider two sets \(\mathcal{C}\) and \(\mathcal{D}\) and suppose to be interested in a specific (unknown) mapping \(F:\mathcal{C}\rightarrow \mathcal{D}\).

 

The data available can be of two types:

  1. Direct measurements of \(F\):                                                        \(\mathcal{T} = \{(x_i,y_i=F(x_i)\}_{i=1,...,N}\subset\mathcal{C}\times\mathcal{D}\)
  2. Indirect measurements that characterize \(F\):                    \(\mathcal{I} = \{(x_i,z_i=G(F(x_i))\}_{i=1,...,N}\subset\mathcal{C}\times G(\mathcal{D})\)

GOAL: Approximate \(F\) on all \(\mathcal{C}\).

(+ reproduce qualitative behaviour of \(F\) )

Examples of these tasks

What are neural networks

They are compositions of parametric functions

\( \mathcal{NN}(x) = f_{\theta_k}\circ ... \circ f_{\theta_1}(x)\)

Examples

\(f_{\theta}(x) = x + B\Sigma(Ax+b),\quad \theta = (A,B,b)\)

ResNets

Feed Forward

Networks

\(f_{\theta}(x) = B\Sigma(Ax+b),\quad \theta = (A,B,b)\)

\(\Sigma(z) = [\sigma(z_1),...,\sigma(z_n)],\quad \sigma:\mathbb{R}\rightarrow\mathbb{R}\)

Approximating Hamiltonians of constrained mechanical systems

  • Celledoni, E., Leone, A., Murari, D., Owren, B., JCAM (2022). Learning Hamiltonians of constrained mechanical systems.

Definition of the problem

\dot{x}(t) = f(x(t))\in\mathbb{R}^m

GOAL : approximate the unknown \(f\) on \(\Omega\)

DATA:

\{(y_i^0,y_i^1,...,y_i^M)\}_{i=1,...,N},\\ y_i^0\in\Omega\subset\mathbb{R}^m
y_i^j = \Phi_f^{j\Delta t}(y_i^0) + \delta_i^j
\Delta t>0

Approximation of a dynamical system

Introduce a parametric model

\dot{x}(t) = \hat{f}_{\theta}(x(t))
\text{solve}\quad \min_{\theta} \sum_{i=1}^N \sum_{j=1}^M \left\|y_i^j - \hat{y}_i^{j}\right\|^2 = \min_{\theta}\mathcal{L}_{\theta}

1️⃣

3️⃣

Choose any numerical integrator applied to \(\hat{f}_{\theta}\)

\hat{y}_i^0 = y_i^0,\,\,\hat{y}_i^{j+1} = \Psi_{\theta}^{\Delta t}(\hat{y}_i^{j})

2️⃣

f(q,p) = \mathbb{J}\nabla H(q,p)=\begin{bmatrix} \partial_p H(q,p) \\ -\partial_q H(q,p)\end{bmatrix},
H:\mathbb{R}^{2n}\rightarrow\mathbb{R},\quad \mathbb{J} = \begin{bmatrix} 0_n & I_n \\ -I_n & 0_n \end{bmatrix}\in\mathbb{R}^{2n\times 2n}

Choice of the model:

\hat{f}_{\theta}(q,p) = \mathbb{J}\nabla H_{\theta}(q,p)
H_{\theta}(q,p) = \frac{1}{2}p^TA^TAp + Net_{\bar{\theta}}(q),\quad \theta = (A,\bar{\theta})

Unconstrained Hamiltonian systems

Unconstrained Hamiltonian systems

f(q,p) = \mathbb{J}\nabla H(q,p)=\begin{bmatrix} \partial_p H(q,p) \\ -\partial_q H(q,p)\end{bmatrix},
H:\mathbb{R}^{2n}\rightarrow\mathbb{R},\quad \mathbb{J} = \begin{bmatrix} 0_n & I_n \\ -I_n & 0_n \end{bmatrix}\in\mathbb{R}^{2n\times 2n}

Choice of the model:

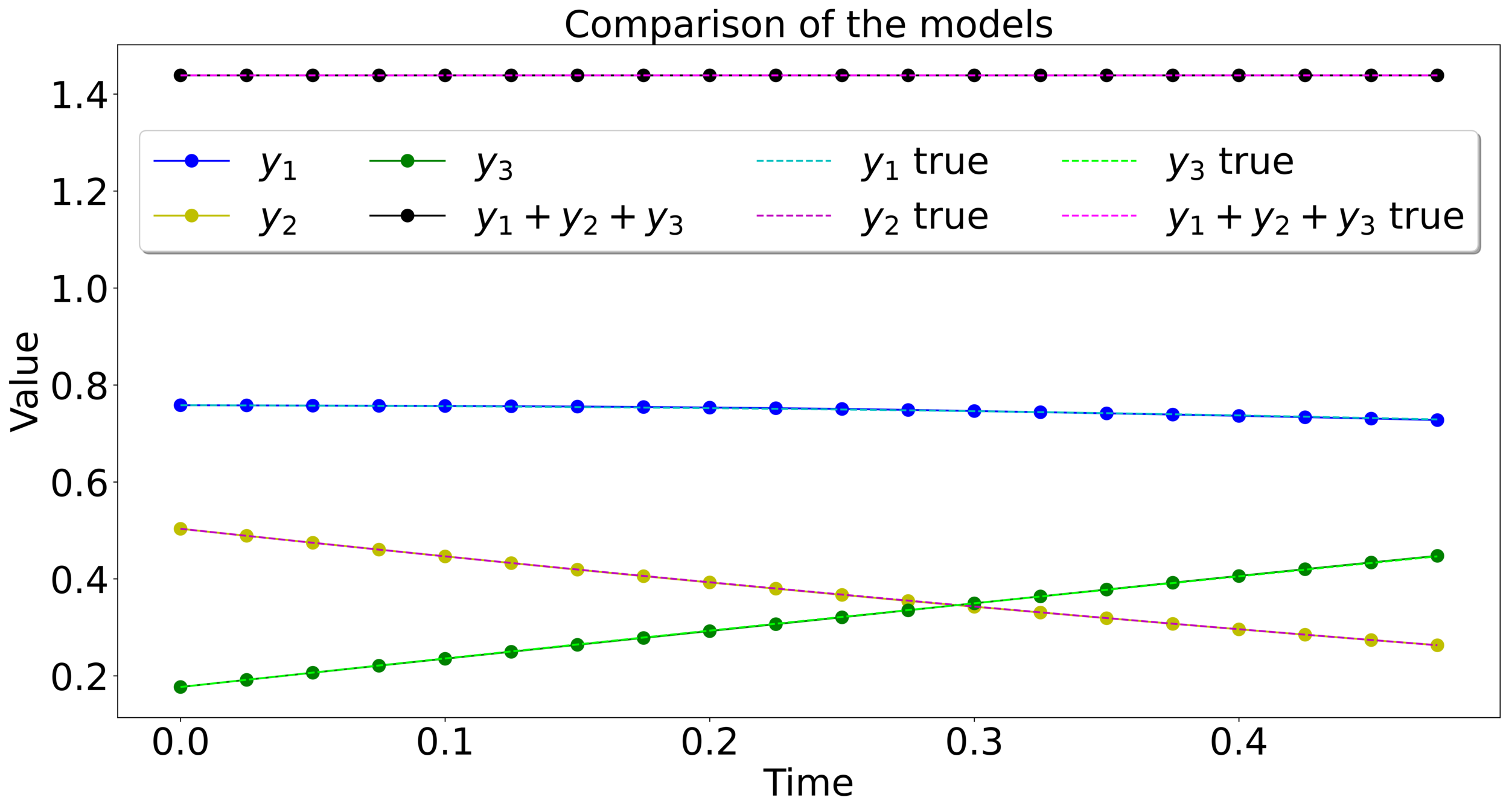
\hat{f}_{\theta}(q,p) = \mathbb{J}\nabla H_{\theta}(q,p)
H_{\theta}(q,p) = \frac{1}{2}p^TA^TAp + Net_{\bar{\theta}}(q),\quad \theta = (A,\bar{\theta})

Measuring the approximation quality

\mathcal{E}_1 = \frac{1}{\bar{N}\bar{M}}\sum_{i=1}^{\bar{N}}\sum_{j=1}^{\bar{M}}\left\|z_i^j - \hat{z}_i^j\right\|^2
z_i^{j+1} = \tilde{\Psi}^{\Delta t}_{H}(z_i^j),\quad \hat{z}_i^{j+1} = \tilde{\Psi}^{\Delta t}_{H_{\theta}}(\hat{z}_i^j)
\mathcal{E}_{2}=\frac{1}{\bar{N}} \sum_{i=1}^{\bar{N}}\left|H\left(\bar{x}_{i}\right)-H_{\theta}\left(\bar{x}_{i}\right)-\frac{1}{\bar{N}} \sum_{l=1}^{\bar{N}}\left(H\left(\bar{x}_{l}\right)-H_{\theta}\left(\bar{x}_{l}\right)\right)\right|
\hat{z}_i^0 = z_i^0 = \bar{x}_i

Test initial conditions

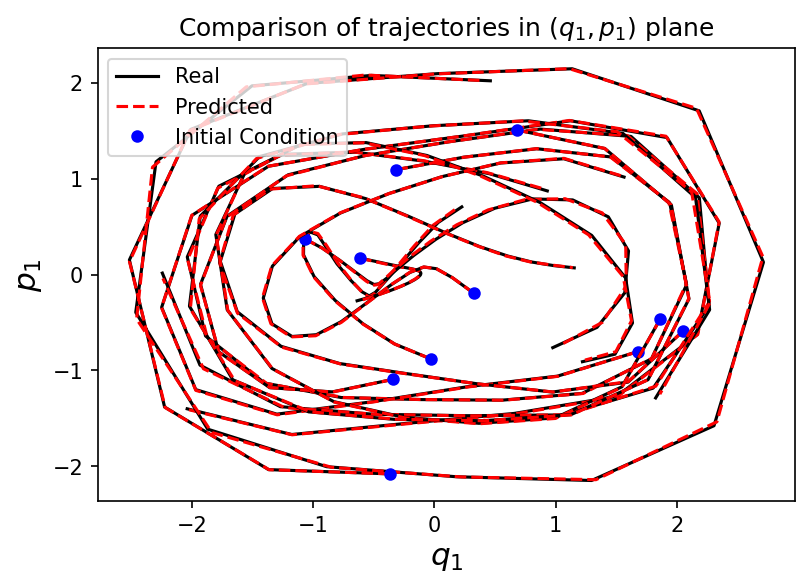
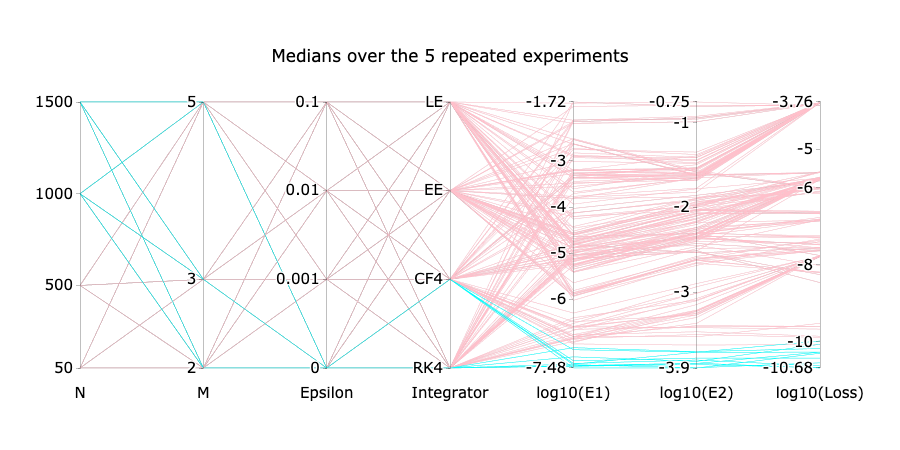
Numerical experiment

H(q, p)=\frac{1}{2}\left[\begin{array}{ll} p_{1} & p_{2} \end{array}\right]^{T}\left[\begin{array}{cc} 5 & -1 \\ -1 & 5 \end{array}\right]\left[\begin{array}{l} p_{1} \\ p_{2} \end{array}\right]+\frac{q_{1}^{4}+q_{2}^{4}}{4}+\frac{q_{1}^{2}+q_{2}^{2}}{2}

⚠️ The integrator used in the test, can be different from the training one.

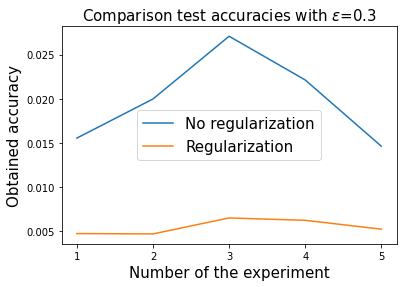
Physics informed regularization

If there is a known conserved quantity \(I(x(t))=I(x(0))\) we can add it to the loss, to get a physics informed regularization:

\mathcal{L}_{\theta}^R = \mathcal{L}_{\theta} + \gamma \sum_{i=1}^N\sum_{j=1}^M |I(\hat{y}_i^j)-I(x_i)|
H\left(x\right)=\frac{q_{1}^{2}+p_{1}^{2}}{2}+\frac{p_{2}^{2}}{2}+\frac{1}{2} q_{2}^{2}+\frac{1}{4} q_{2}^{4}\\ =h_{1}\left(q_{1}, p_{1}\right)+h_{2}\left(q_{2}, p_{2}\right)
\delta_i^j = \varepsilon n_i^j,\,n_i^j\sim \mathcal{N}(0,1)
I = h_1

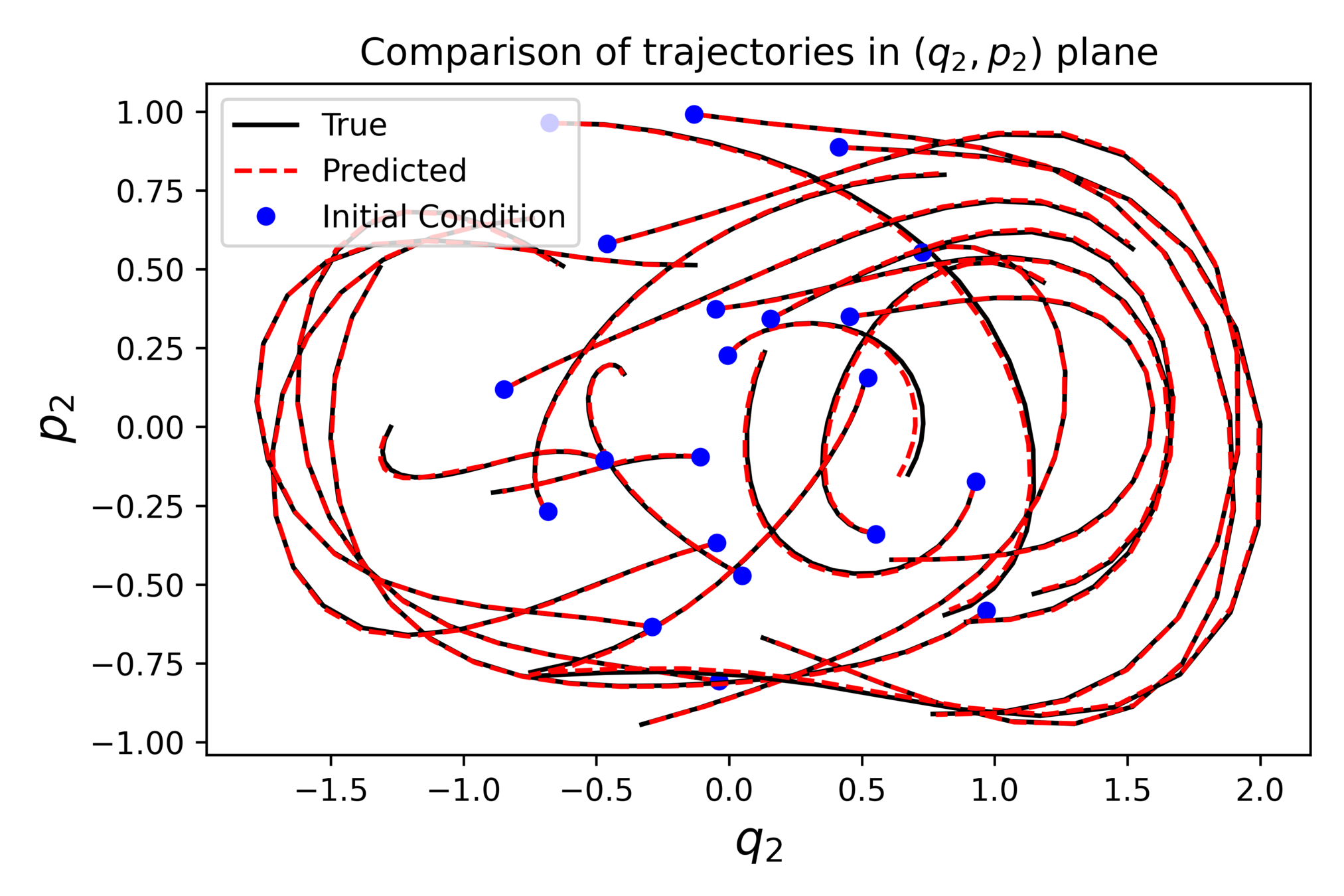
On clean trajectories

Constrained Hamiltonian systems

\begin{cases} \dot{x}(t) = \mathbb{J}\nabla H(q,p),\quad x=(q,p)\\ g(q) = 0,\quad g:\mathbb{R}^n\rightarrow\mathbb{R}^m \end{cases}
\mathcal{M} = T^*\mathcal{Q}=T^*\{q\in\mathbb{R}^n:\,g(q)=0\} = \\ \{(q,p)\in\mathbb{R}^{2n}:\,g(q)=0,\,G(q)\partial_pH(q,p)=0\}
\mathcal{Q}=\{q\in\mathbb{R}^n:\;g(q)=0\}\subset\mathbb{R}^n

Modelling the vector field on \(\mathcal{M}\)

P(q) : \mathbb{R}^n\rightarrow T_q\mathcal{Q},\,v\mapsto P(q)v
T_q\mathcal{Q} = \{v\in\mathbb{R}^n:\,G(q)v=0\}
\begin{cases} \dot{q}=P(q) \partial_{p} H(q, p) \\ \dot{p}=-P(q)^{T} \partial_{q} H(q, p)+W(q, p) \partial_{p} H(q, p) \end{cases}

On \(\mathcal{M}\) the dynamics can be written as

⚠️  On \(\mathbb{R}^{2n}\setminus\mathcal{M}\) the vector field extends non-uniquely.

Example with \(\mathcal{Q}=S^2\)

\mathcal{Q}=\{q\in\mathbb{R}^3:\;\|q\|^2-1=0\}\subset\mathbb{R}^3,\\ dim\mathcal{Q}=2
P(q) : \mathbb{R}^3\rightarrow T_q\mathcal{Q},\,v\mapsto (I_3-qq^T)v
T_q\mathcal{Q} = \{v\in\mathbb{R}^3:\,q^Tv=0\}
\begin{cases} \dot{q} &=\left(I-q q^{T}\right) \partial_{p} H(q, p) \\ \dot{p} &=-\left(I-q q^{T}\right) \partial_{q} H(q, p)+\partial_{p} H(q, p) \times(p \times q) \end{cases}

On \(\mathcal{M}\) the dynamics can be written as

Learning constrained Hamiltonian systems

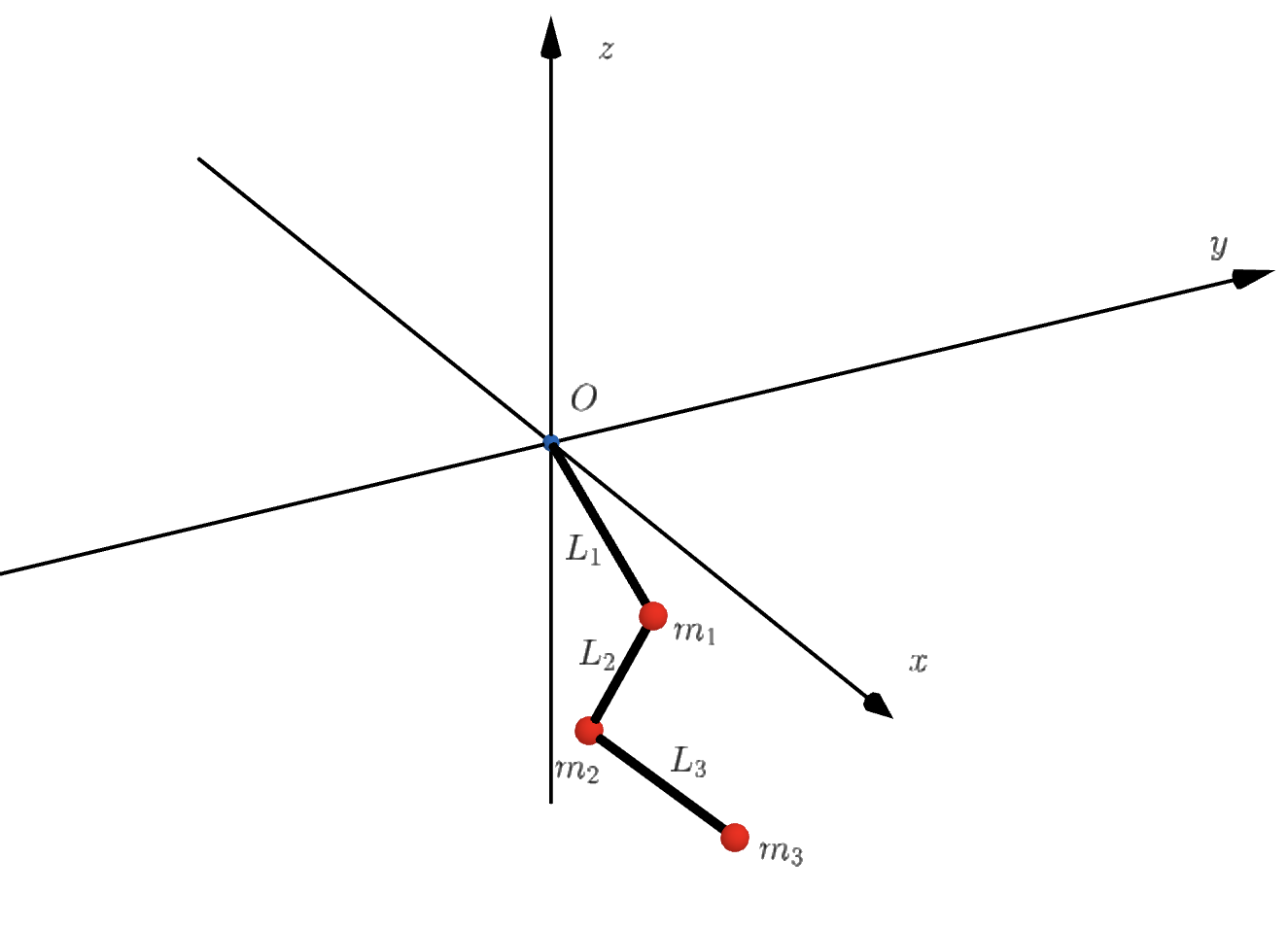
\hat{f}_{\theta}(q,p) = \begin{bmatrix} P(q) \partial_{p} H_{\theta}(q, p) \\ -P(q)^{T} \partial_{q} H_{\theta}(q, p)+W(q, p) \partial_{p} H_{\theta}(q, p) \end{bmatrix}
H_{\theta}(q, p)=\frac{1}{2} p^{T} M_{\theta_{1}}^{-1}(q) p+\operatorname{Net}_{\theta_{2}}(q), \\ \theta=\left(\theta_{1}, \theta_{2}\right)

Chain of spherical pendula

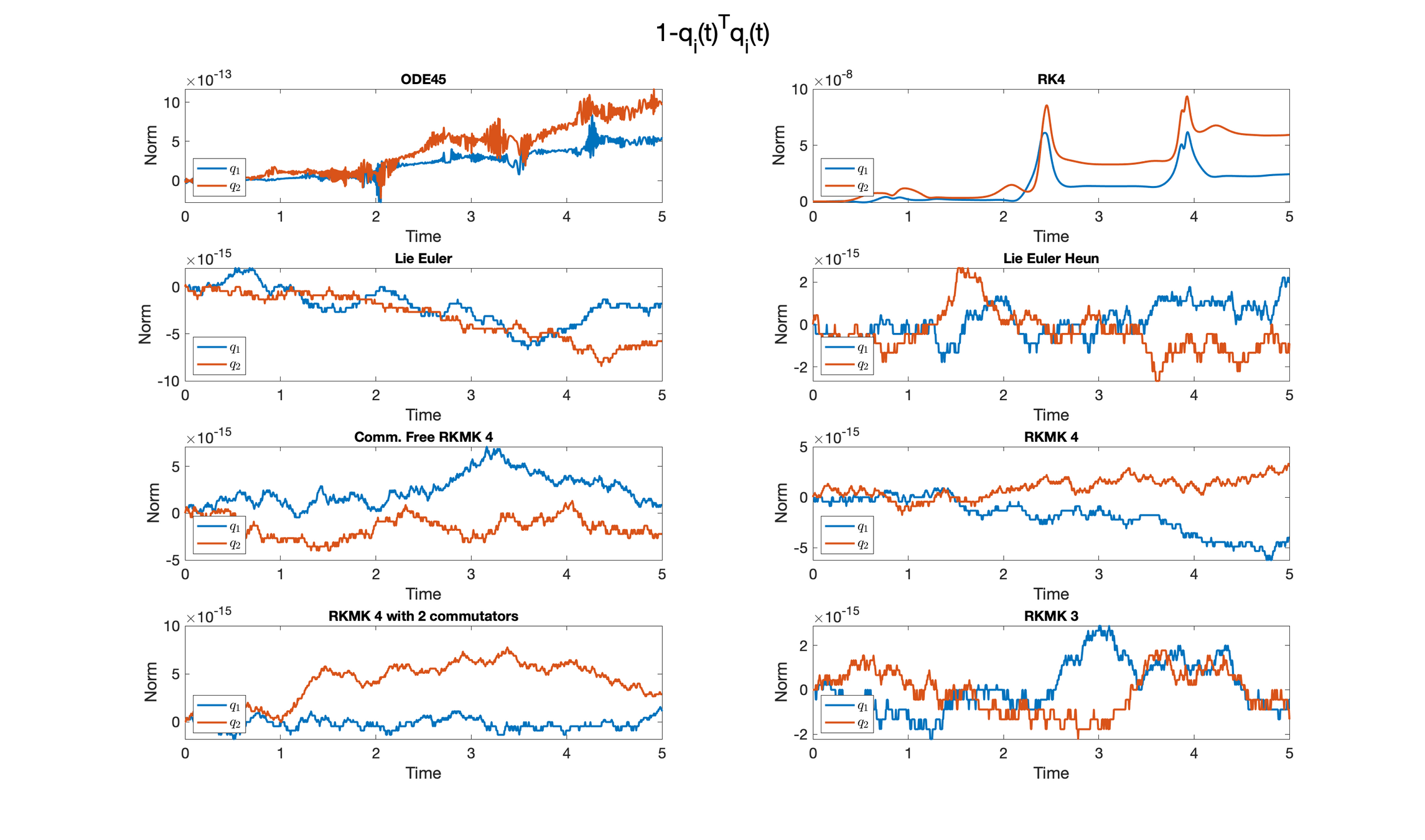
Choosing the numerical method for the training

Example with the double spherical pendulum

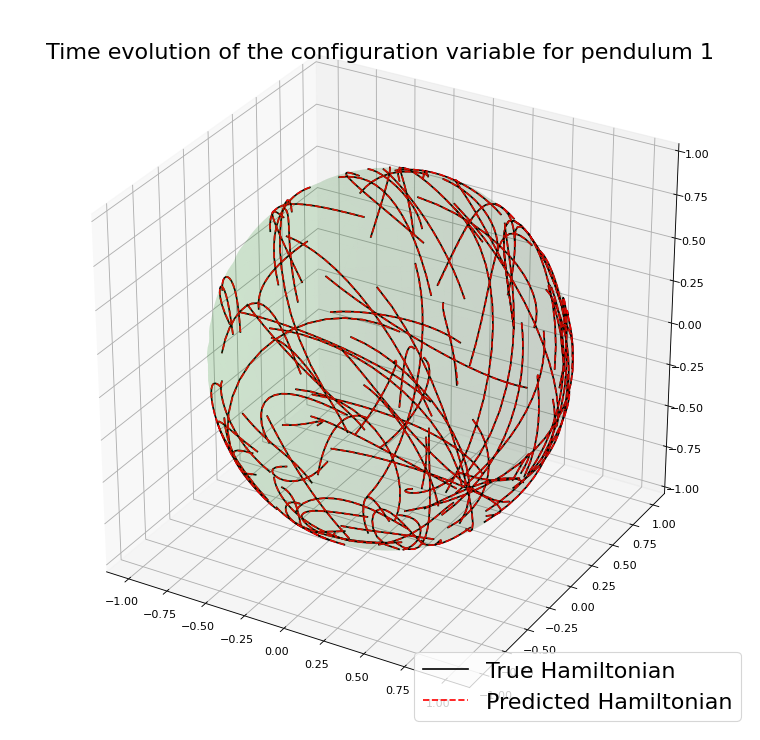
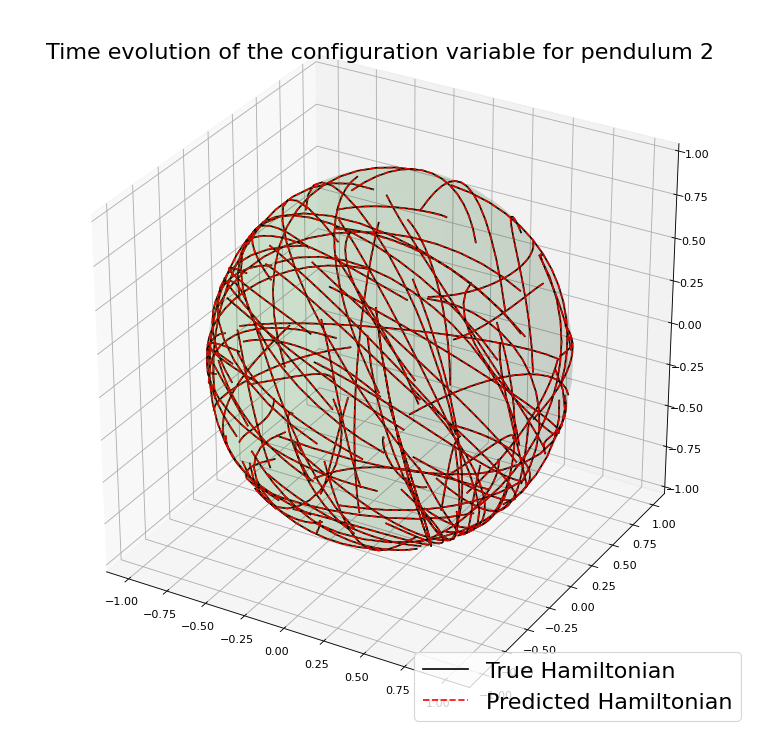
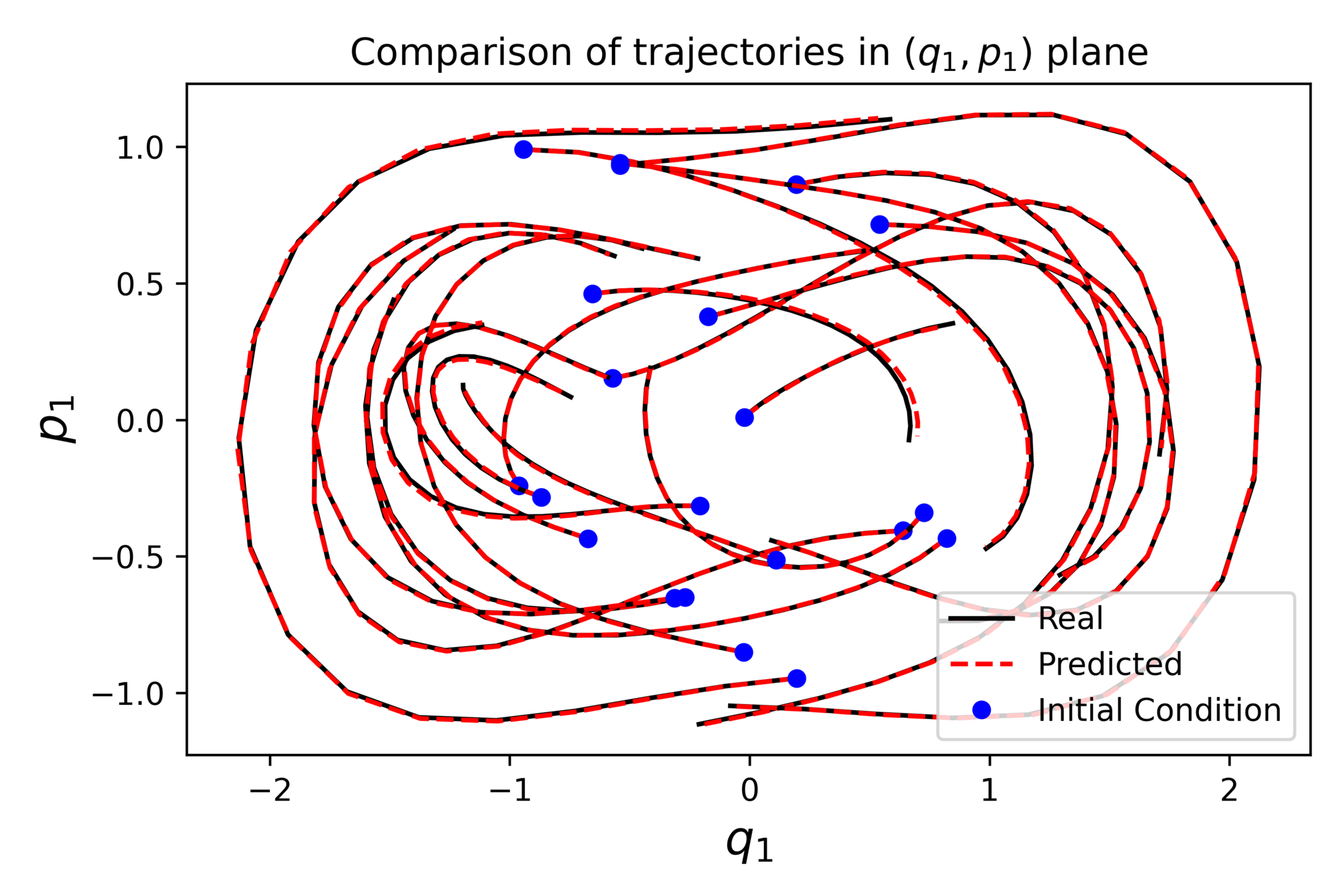
A case where preserving \(\mathcal{M}\) helps

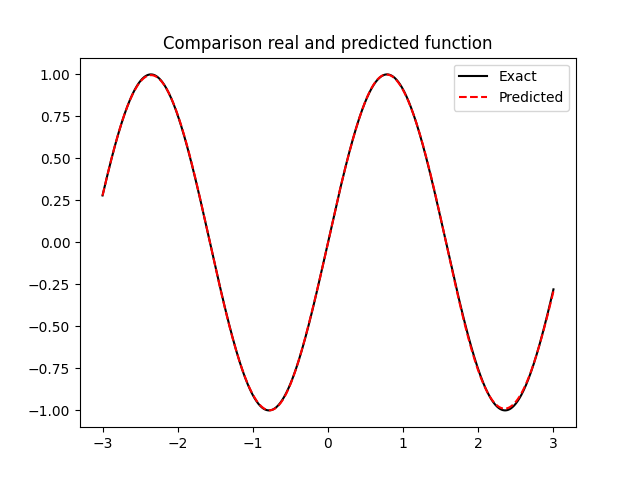
Suppose to have just few unknown elements in the expression of the Hamiltonian

As a consequence, one expects a very accurate approximation.

 

Example with the spherical pendulum:

H_{\theta}(q, p)=\frac{1}{2 m} p^{T} p+u^{T} q, \quad m>0, u \in \mathbb{R}^{3}

Similar results preserving \(\mathcal{M}\)

Designing and studying ResNets with dynamical systems' theory

  • Celledoni, E., Murari D., Owren B., Schönlieb C.B., Sherry F, preprint (2022). Dynamical systems' based neural networks

Neural networks motivated by dynamical systems

\( \mathcal{N}(x) = f_{\theta_M}\circ ... \circ f_{\theta_1}(x)\)

\mathcal{N}(x) = \Psi_{F_M}^{h_M}\circ ...\circ \Psi_{F_1}^{h_1}(x)

\( \dot{x}(t) = F(x(t),\theta(t))=:F_{s(t)}(x(t)) \)

Where \(F_i(x) = F(x,\theta_i)\)

\( \theta(t)\equiv \theta_i,\,\,t\in [t_i,t_{i+1}),\,\, h_i = t_{i}-t_{i-1}\)

t_0
t_1
t_2
t_i
t_{i+1}
t_M
\cdots
\cdots
\cdots

Neural networks motivated by dynamical systems

\dot{x}(t) = B(t)\mathrm{tanh}(A(t)x(t) + b(t))

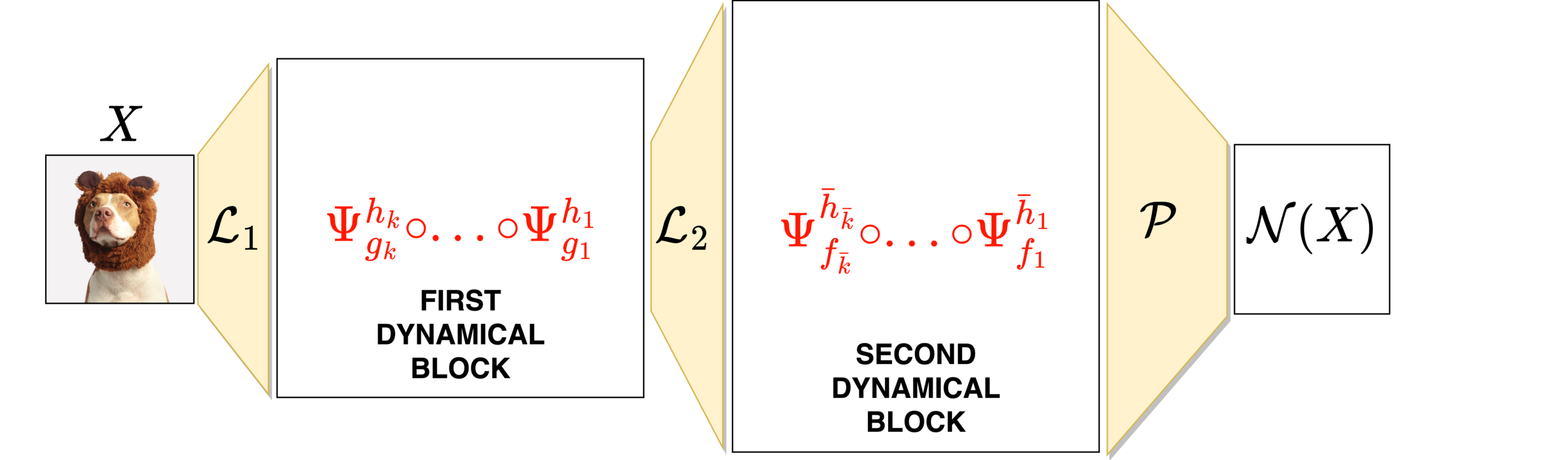
Neural networks motivated by dynamical systems

Accuracy is not all you need

\(X\) , Label : Plane

\(X+\delta\), \(\|\delta\|_2=0.3\) , Label : Cat

GENERAL IDEA

EXAMPLE

Property \(\mathcal{P}\)

\(\mathcal{P}=\) Volume preservation

Family \(\mathcal{F}\) of vector fields that satisfy \(\mathcal{P}\)

\(F_{\theta}(x,v) = \begin{bmatrix} \Sigma(Av+a) \\ \Sigma(Bx+b)  \end{bmatrix} \)

\(\mathcal{F}=\{F_{\theta}:\,\,\theta\in\mathcal{P}\}\)

Integrator \(\Psi^h\) that preserves \(\mathcal{P}\)

x_{n+1}=x_n+h\Sigma(A_nv_n+a_n)\\ v_{n+1}=v_n+h\Sigma(B_nx_{n+1}+b_n)

Imposing some structure

GENERAL IDEA

EXAMPLE

Property \(\mathcal{P}\)

\(\mathcal{P}=\) Volume preservation

Family \(\mathcal{F}\) of vector fields that satisfy \(\mathcal{P}\)

\(F_{\theta}(x,v) = \begin{bmatrix} \Sigma(Av+a) \\ \Sigma(Bx+b)  \end{bmatrix} \)

\(\mathcal{F}=\{F_{\theta}:\,\,\theta\in\mathcal{P}\}\)

Integrator \(\Psi^h\) that preserves \(\mathcal{P}\)

x_{n+1}=x_n+h\Sigma(A_nv_n+a_n)\\ v_{n+1}=v_n+h\Sigma(B_nx_{n+1}+b_n)

Imposing some structure

GENERAL IDEA

EXAMPLE

Property \(\mathcal{P}\)

\(\mathcal{P}=\) Volume preservation

Family \(\mathcal{F}\) of vector fields that satisfy \(\mathcal{P}\)

\(F_{\theta}(x,v) = \begin{bmatrix} \Sigma(Av+a) \\ \Sigma(Bx+b)  \end{bmatrix} \)

\(\mathcal{F}=\{F_{\theta}:\,\,\theta\in\mathcal{P}\}\)

Integrator \(\Psi^h\) that preserves \(\mathcal{P}\)

x_{n+1}=x_n+h\Sigma(A_nv_n+a_n)\\ v_{n+1}=v_n+h\Sigma(B_nx_{n+1}+b_n)

Imposing some structure

Examples

\dot{x}(t) = -A^T(t)\Sigma(A(t)x(t) + b(t)) =\\ -\nabla \left( \boldsymbol{1}^T\Gamma(A(t)x(t)+b(t)) \right)
\dot{x}(t) = \mathbb{J}A^T(t)\Sigma(A(t)x(t)+b(t))
\ddot{x}(t) = \Sigma(A(t)x(t)+b(t))

1-LIPSCHITZ NETWORKS

HAMILTONIAN NETWORKS

VOLUME PRESERVING, INVERTIBLE

\dot{y} = \begin{bmatrix} 0 & -y_3y_1^2 & y_2y_3 \\ y_3y_1^2 & 0 & -\sin{y_1} \\ -y_2y_3 & \sin{y_1} & 0\end{bmatrix}\boldsymbol{1}
\dot{x}(t) = \{A_{\theta}(x(t))-A_{\theta}(x(t))^T\}\boldsymbol{1}\\ \mathrm{vec}(A_{\theta}(x)) = \Sigma(Ux+u)

Mass-preserving networks

Lipschitz-constrained networks

\(m=1\)

\(m=\frac{1}{2}\)

\(\Sigma(x) = \max\left\{x,\frac{x}{2}\right\}\)

X_{\theta_i}(x) := - \nabla V_{\theta_i}(x) = -A_i^T\Sigma(A_ix+b_i)
\Psi^{h_C}_{X_{\theta_i}}(x) = x - {h_C}A_i^T\Sigma(A_ix+b_i)
Y_{\theta_i}(x) := W_i^T\Sigma(W_ix + v_i)
\|\Psi^{h_C}_{X_{\theta_i}}(y) - \Psi^{h_C}_{X_{\theta_i}}(x)\|\leq \sqrt{1-{h_C}+{h_C}^2}\|y-x\|
\Psi^{h_E}_{Y_{\theta_i}}(x) = x + {h_E}W_i^T\Sigma(W_ix+v_i)
\|\Psi^{h_E}_{Y_{\theta_i}}(y) - \Psi^{h_E}_{Y_{\theta_i}}(x)\|\leq (1+{h_E})\|y-x\|

Lipschitz-constrained networks

\mathcal{N}(x)=\Psi_{X_{\theta_{2k}}}^{h_{2k}} \circ \Psi_{Y_{\theta_{2k-1}}}^{h_{2k-1}} \circ ... \circ \Psi_{X_{\theta_2}}^{h_2} \circ \Psi_{Y_{\theta_{1}}}^{h_1}(x)

 We impose :

\|\mathcal{N}(x)-\mathcal{N}(y)\|\leq \|x-y\|
\sqrt{1-{h_C}+{h_C}^2}(1+h_E)\leq 1

Lipschitz-constrained networks

Adversarial robustness

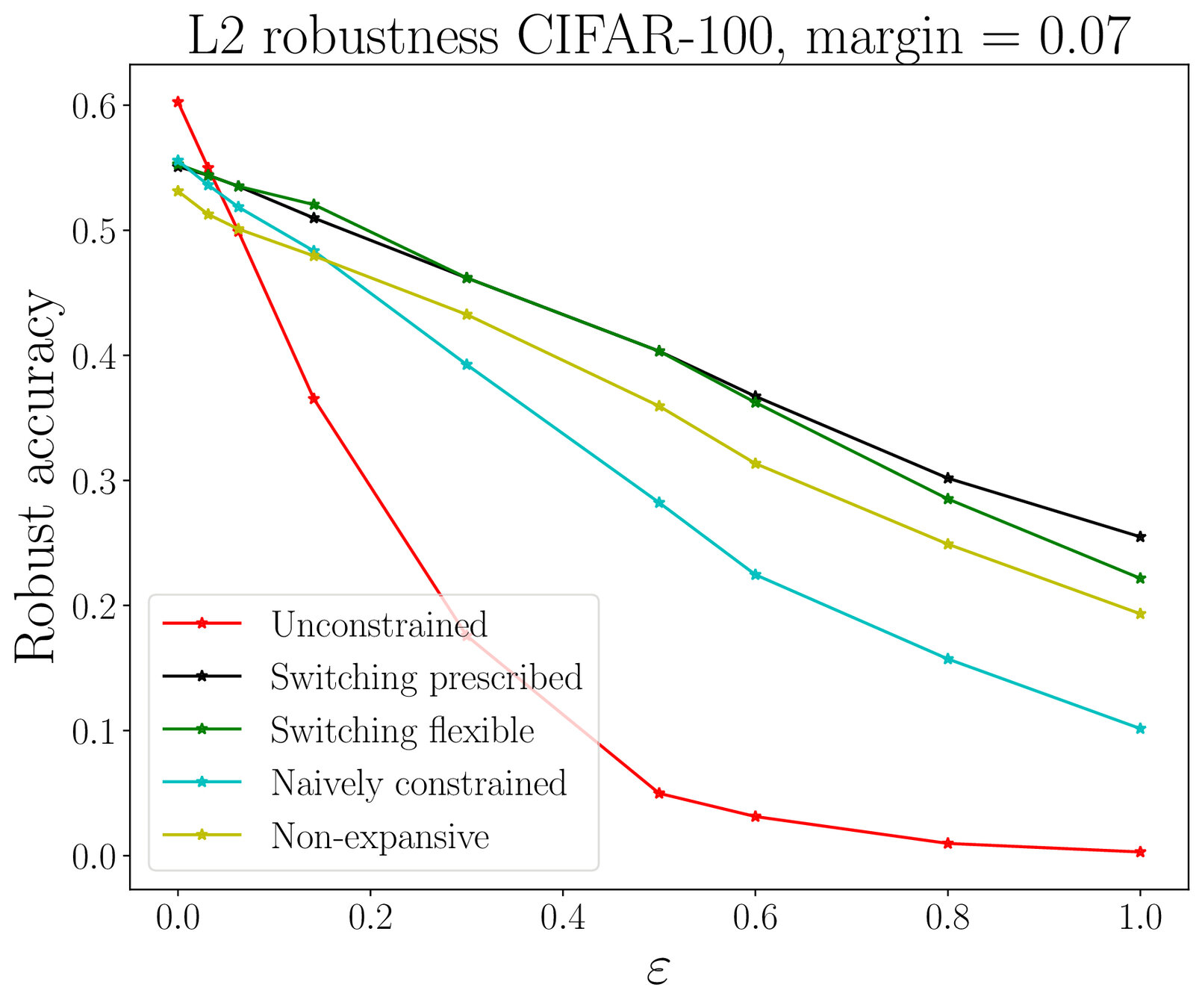
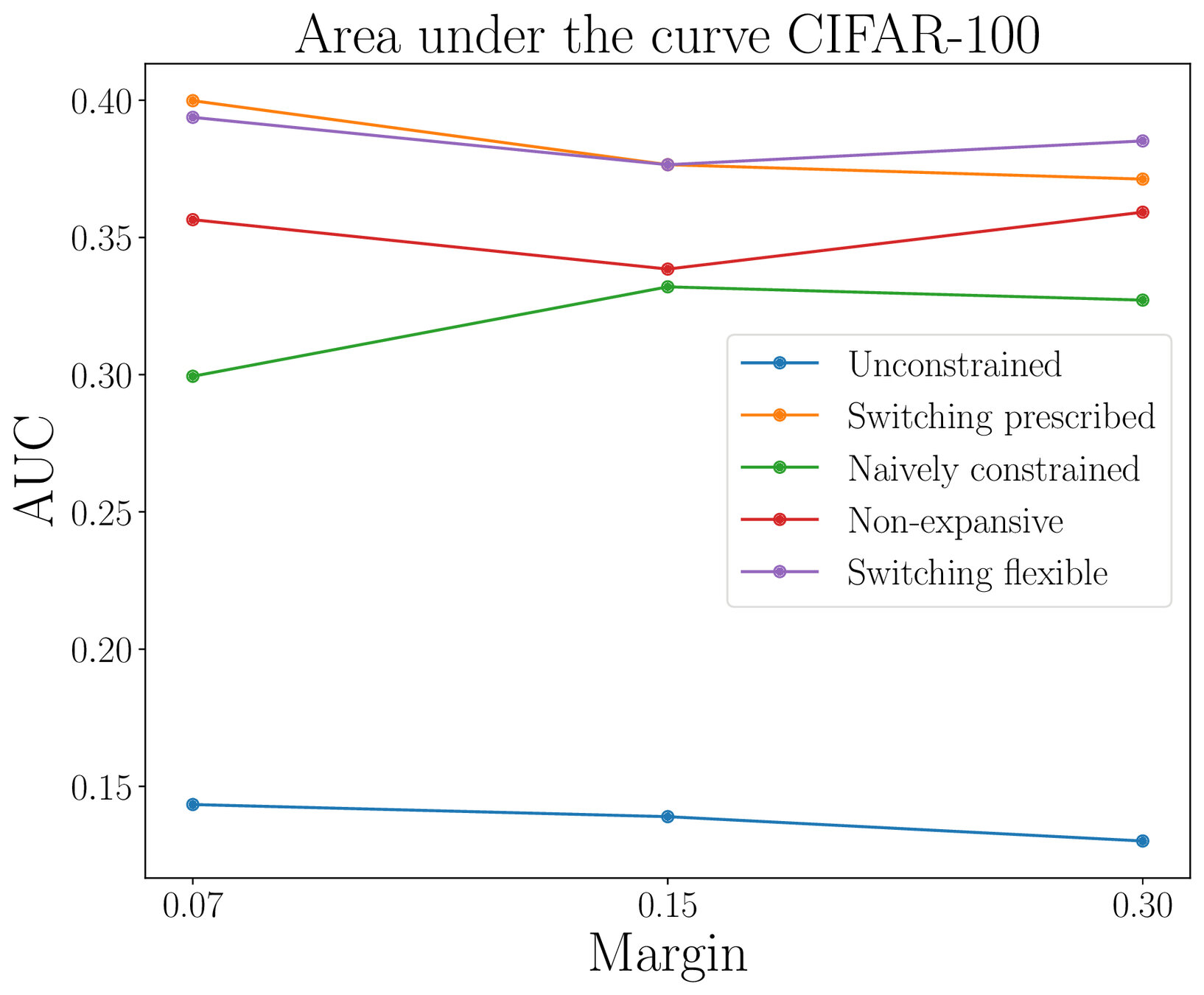
Thank you for the attention

Case with \(\mathcal{M}\) homogeneous

A manifold \(\mathcal{M}\) is homogeneous if there is a Lie group \(\mathcal{G}\) that defines a transitive group action \(\varphi:\mathcal{G}\times\mathcal{M}\rightarrow\mathcal{M}\).

A vector field \(f\) on \(\mathcal{M}\) can be represented as \(f(x) = \varphi_*(\xi(x))(x)\), for a function

\(\xi:\mathcal{M}\rightarrow\mathfrak{g}\simeq T_e\mathcal{G}\).

Lie Group Methods are a class of methods exploiting this structure and preserving \(\mathcal{M}\). The simplest is Lie Euler:

\(y_i^{j+1} = \varphi(\exp(\Delta t \,\xi(y_i^j)),y_i^j)\)

Basic idea of a class of Lie group methods

\(\mathcal{M}\)

\(y_i^j\)

\(y_i^{j+1}=\varphi_g(y_i^j)\)

\(\mathfrak{g}\)

\(\xi\)

\(\exp\)

\(\mathcal{G}\)

\(\varphi_g\)

\(\Psi^{\Delta t}\)

\(0\)

\(\Delta t \xi(y_i^j)\)

\(g=\exp(\Delta t\,\xi(y_i^j))\)

\(f\in\mathfrak{X}(M)\)

\(f^L\in\mathfrak{X}(\mathfrak{g})\)

Made with Slides.com