Dynamical systems' based neural networks

Davide Murari

davide.murari@ntnu.no

What are neural networks

They are compositions of parametric functions

\( \mathcal{NN}(x) = f_{\theta_k}\circ ... \circ f_{\theta_1}(x)\)

Examples

\(f_{\theta}(x) = x + B\Sigma(Ax+b),\quad \theta = (A,B,b)\)

ResNets

Feed Forward

Networks

\(f_{\theta}(x) = B\Sigma(Ax+b),\quad \theta = (A,B,b)\)

\(\Sigma(z) = [\sigma(z_1),...,\sigma(z_n)],\quad \sigma:\mathbb{R}\rightarrow\mathbb{R}\)

Neural networks motivated by dynamical systems

\mathcal{NN}(x) = \Psi_{f_k}^{h_k}\circ ...\circ \Psi_{f_1}^{h_1}(x)

EXPLICIT

EULER

\( \Psi_{f_i}^{h_i}(x) = x + h_i f_i(x)\)

\( \dot{x}(t) = f(t,x(t),\theta(t)) \)

Time discretization : \(0 = t_1 < ... < t_k <t_{k+1}= T \), \(h_i = t_{i+1}-t_{i}\)

Where \(f_i(x) = f(t_i,x,\theta(t_i))\)

EXAMPLE

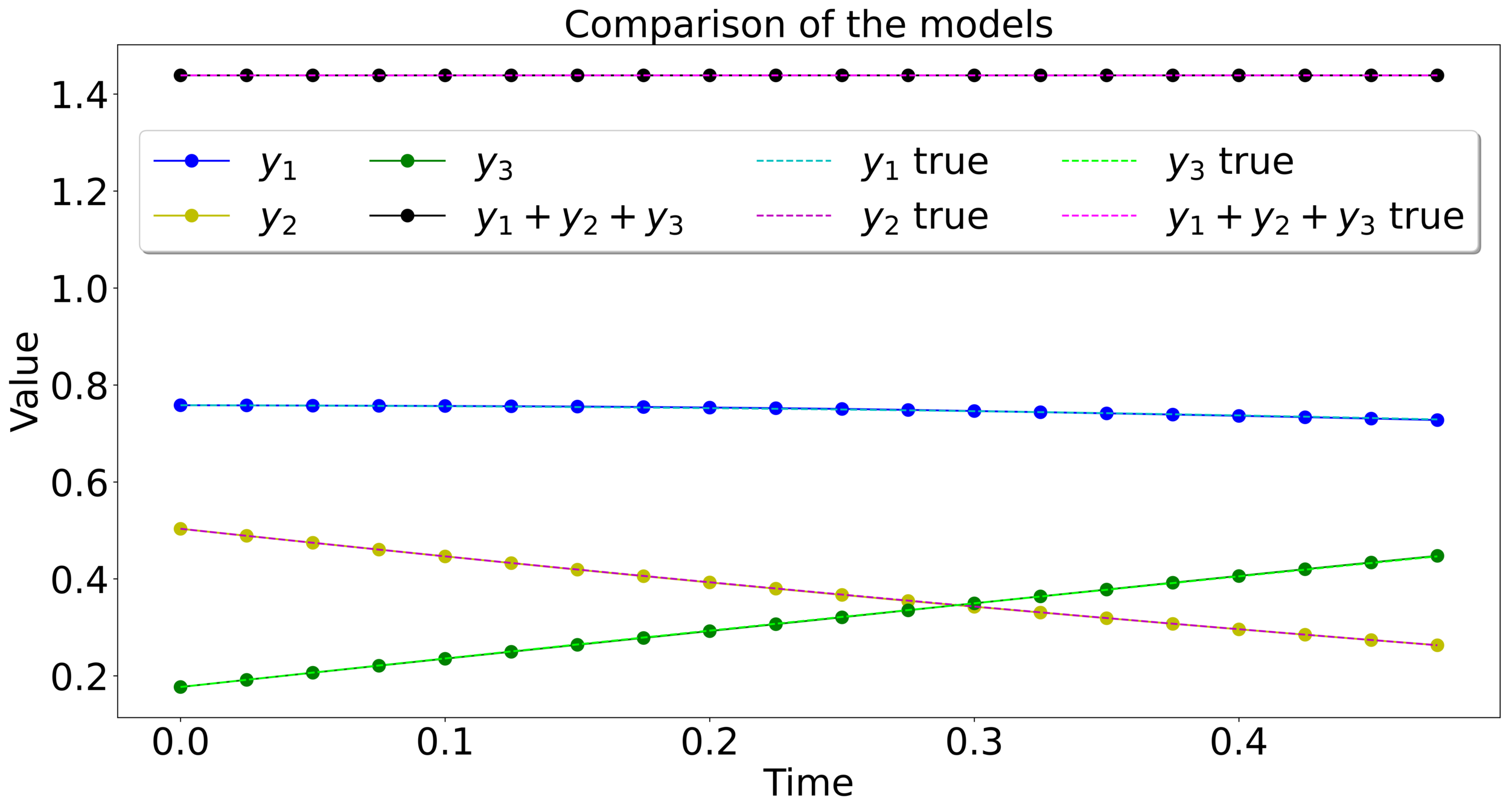
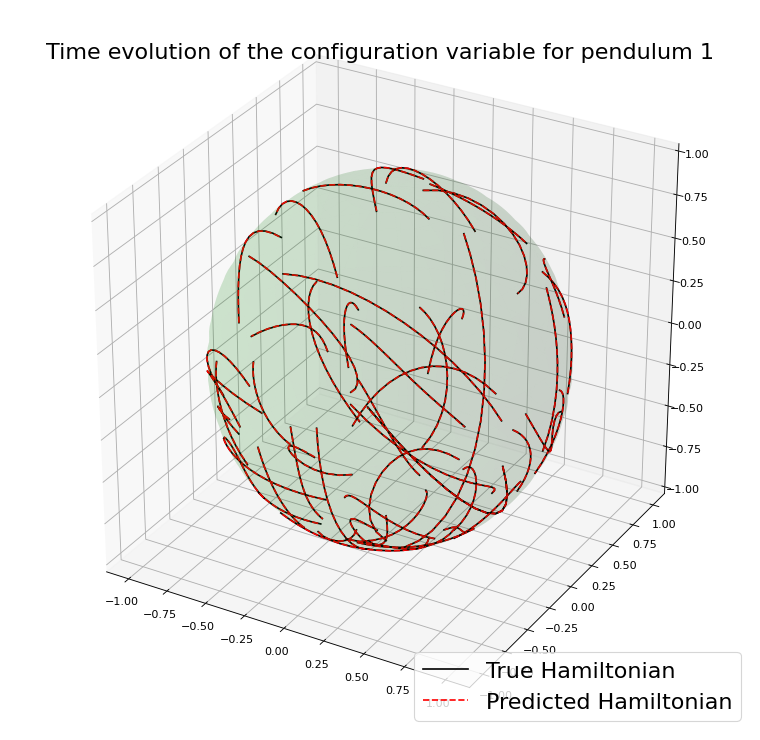
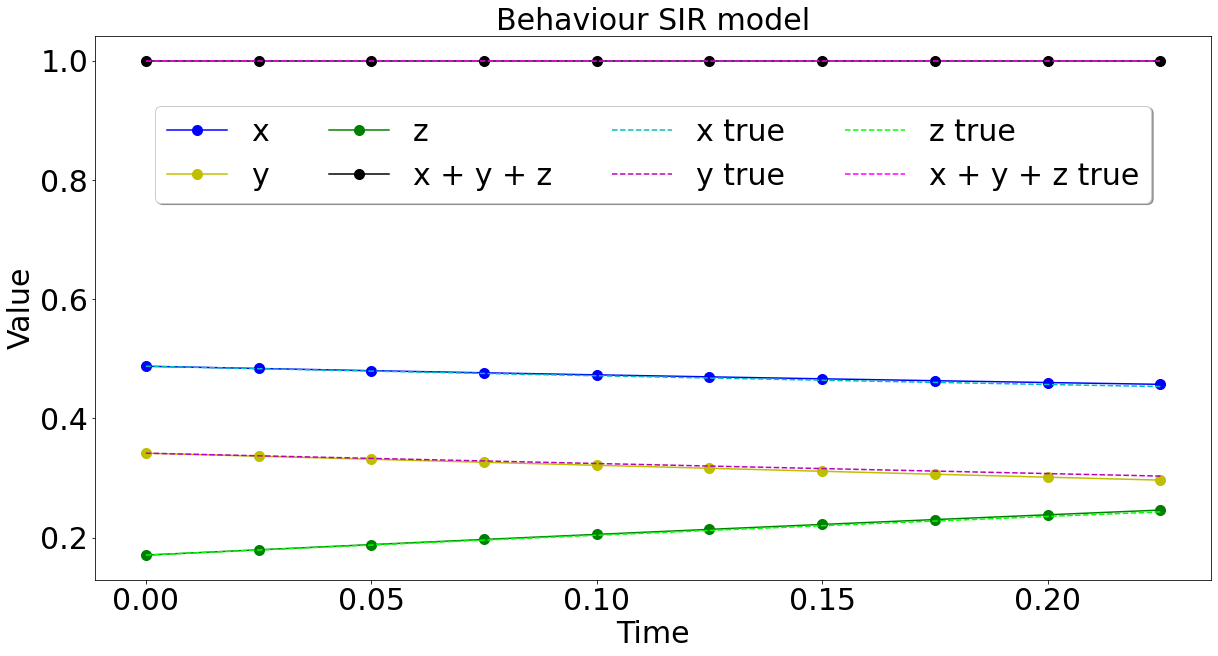
Examples of problems with a specific structure

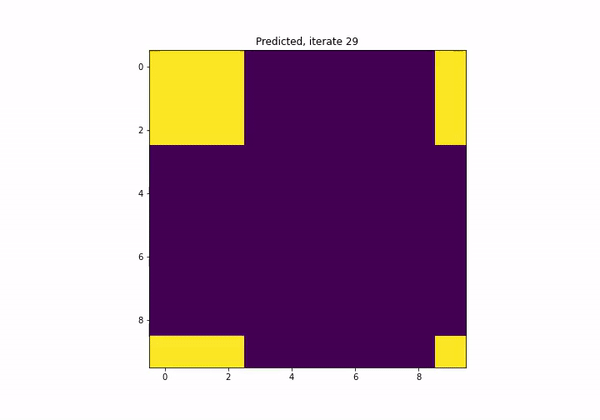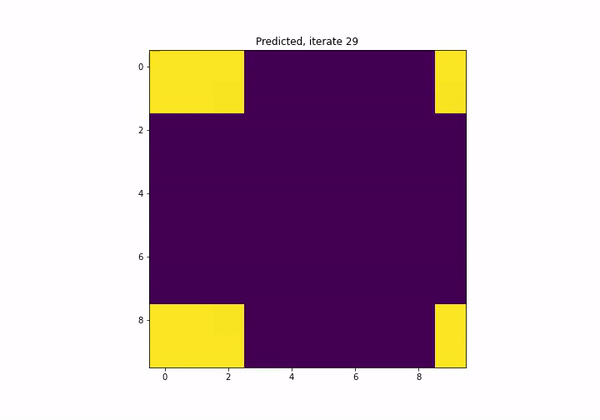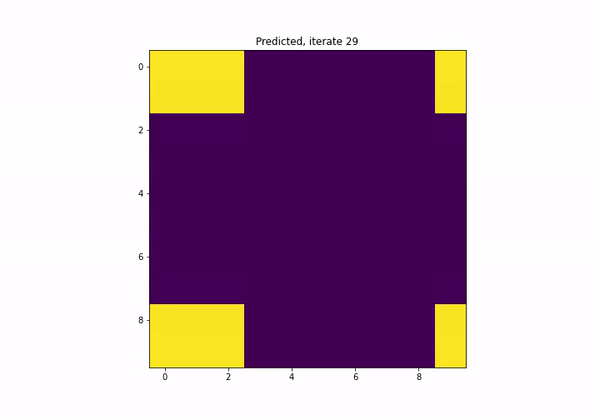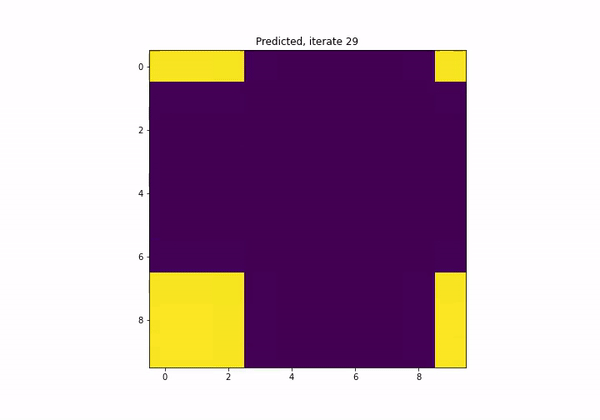
What if I want the model to satisfy a certain property?

GENERAL IDEA

EXAMPLE

Property \(\mathcal{P}\)

\(\mathcal{P}=\)Volume preservation

Family \(\mathcal{F}\) of vector fields that satisfy \(\mathcal{P}\)

\(X_{\theta}(x,v) = \begin{bmatrix} \Sigma(Av+a) \\ \Sigma(Bx+b) \end{bmatrix} \)

\(\mathcal{F}=\{X_{\theta}:\,\,\theta\in\mathcal{A}\}\)

Integrator \(\Psi^h\) that preserves \(\mathcal{P}\)

x_{n+1}=x_n+h\Sigma(Av_n+a)\\ \,\,\,\,v_{n+1}=v_n+h\Sigma(Bx_{n+1}+b)

Choice of dynamical systems

\dot{x}(t) = \{A_{\theta}(x(t))-A_{\theta}(x(t))^T\}\boldsymbol{1}\\ \mathrm{vec}(A_{\theta}(x)) = \Sigma(Ux+u)

MASS-PRESERVING NEURAL NETWORKS

\dot{X}(t) = A_{\theta_1}(X(t))X(t) + X(t)B_{\theta_2}(X(t))\\ A_{\theta_1}(X) = \Sigma(U_1XU_2^T+A),\\ B_{\theta_2}(X) = \Sigma(V_1XV_2^T+B),

\mathrm{rank}(X_0) = r\implies \mathrm{rank}(X(t))=r\,\,\forall t>0

RANK PRESERVING NEURAL NETWORKS

Example

\dot{y} = \begin{bmatrix} 0 & -y_3y_1^2 & y_2y_3 \\ y_3y_1^2 & 0 & -\sin{y_1} \\ -y_2y_3 & \sin{y_1} & 0\end{bmatrix}\boldsymbol{1}