Data Analysis in MRI and PET/MRI Neuroimaging

Davide Poggiali

PhD student, Neurosciences

PyConIE 2016

Some pre-requisites

For a better understanding of this talk, it is suggested some basic mathematical knowledge (sorry...), as 

  • Basis of Linear Algebra
  • Iterative methods for zeros finding

otherwise, don't panic

Python packages for NeuroImaging

nipy family:

  1. nibabel (I/O, good with numpy)
  2. nipy (image processing)
  3. nipype (pipelining, wrapper)
  4. dipy (diffusion)
  5. nilearn (machine learning)

 

numpy

scipy.ndimage

scikit-image

Summary:

  1. Introduction to NeuroImaging

  2. Common use algorithms & pipelines

  3. Image Registration

  4. Patlak plot in PET/MRI

1. Introduction

One of the first brain measurement...

A modern neurological study aims to relate several biomarkers from different sources in order to explain the illness evolution improve prognostic accuracy and optimize the treatment.

A modern research group can have at disposal:

  • clinical,
  • imaging,
  • neuropsychological,
  • liquor biomarkers

Neuroimaging offers a fecund source of biomarkers 

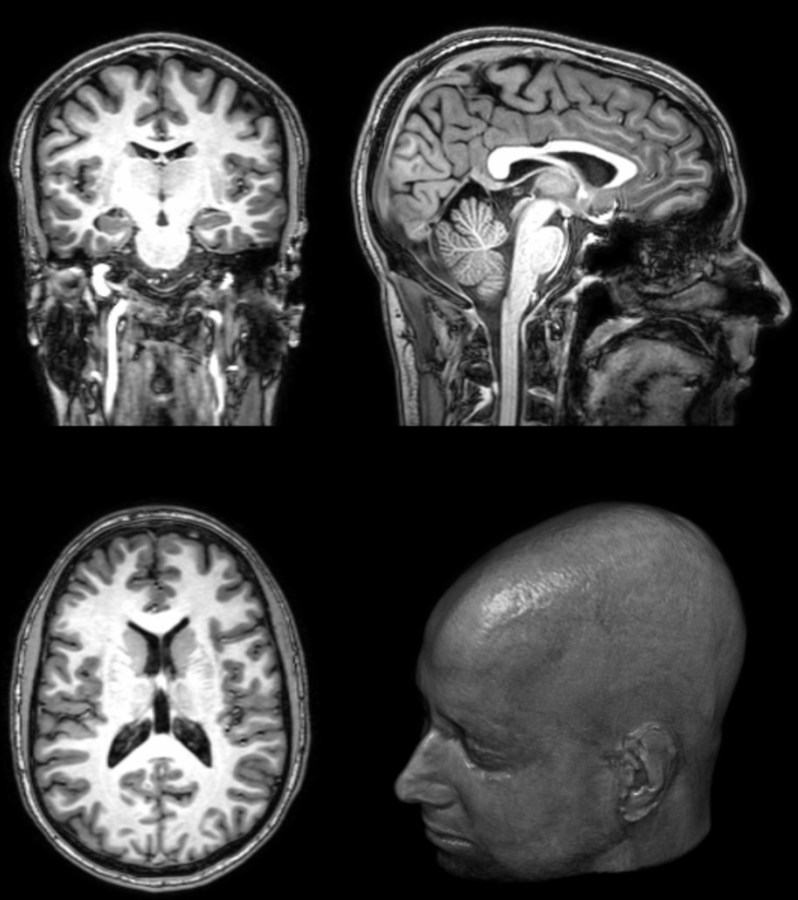
Computing biomarkers from neuroimaging sources can be time-consuming, also because an increasing number of images can be available from a single patient.

For instance, a study involving

  • three 3D MRI images
  • two 2D MRI sequences
  • one dynamic brain PET

of 50 patients occupy more than 2Tb of disk space.

Hence there is need of improving the speed without loss of accuracy whenever possible.

2. Common use algorithms & pipelines

1. Registration (rigid, affine, nonlinear)

 

2. Correction (Bias Field, Lesion Filling,

Motion Correction, PVC)

 

3. Segmentation (Manual, Template-based)

 

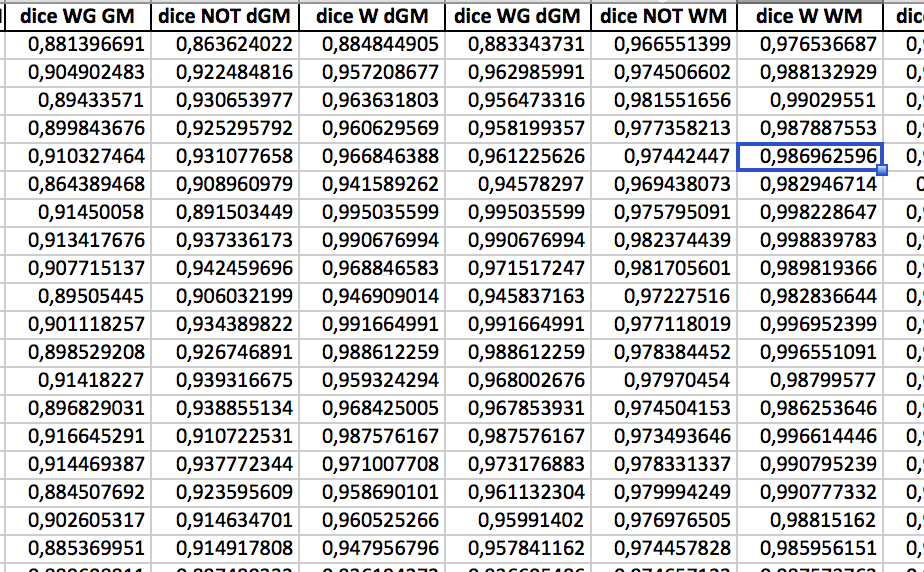
4. Measurement (mean, std over VOIs)

Registration

Correction

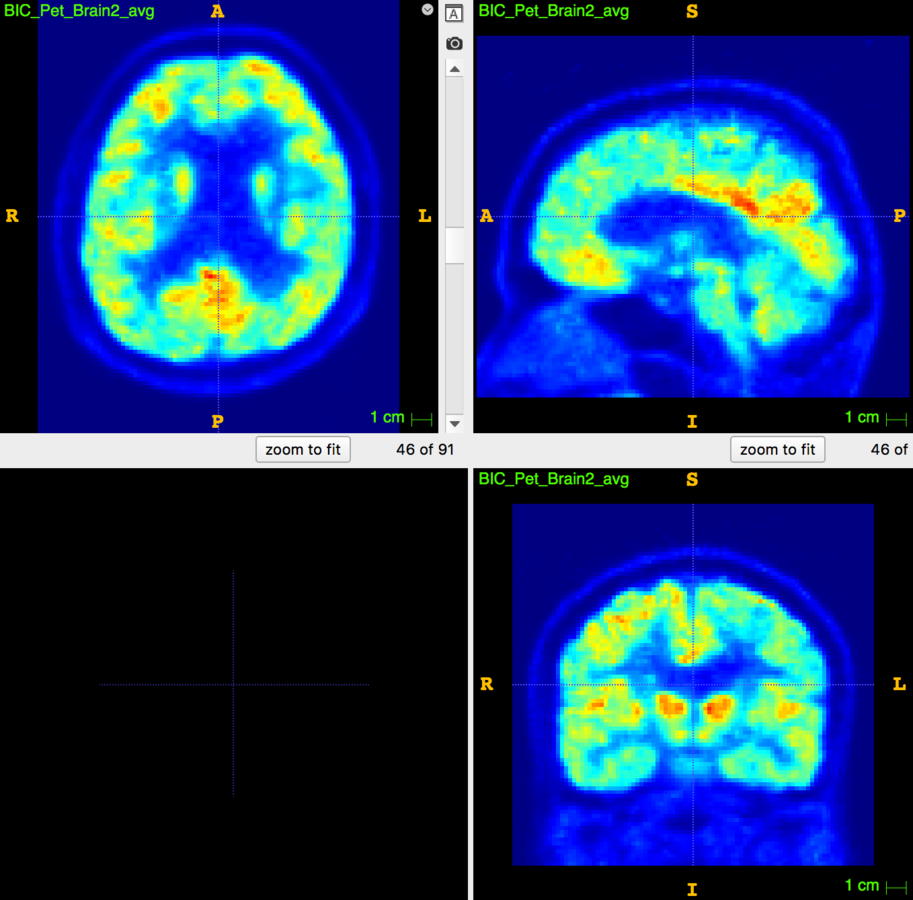
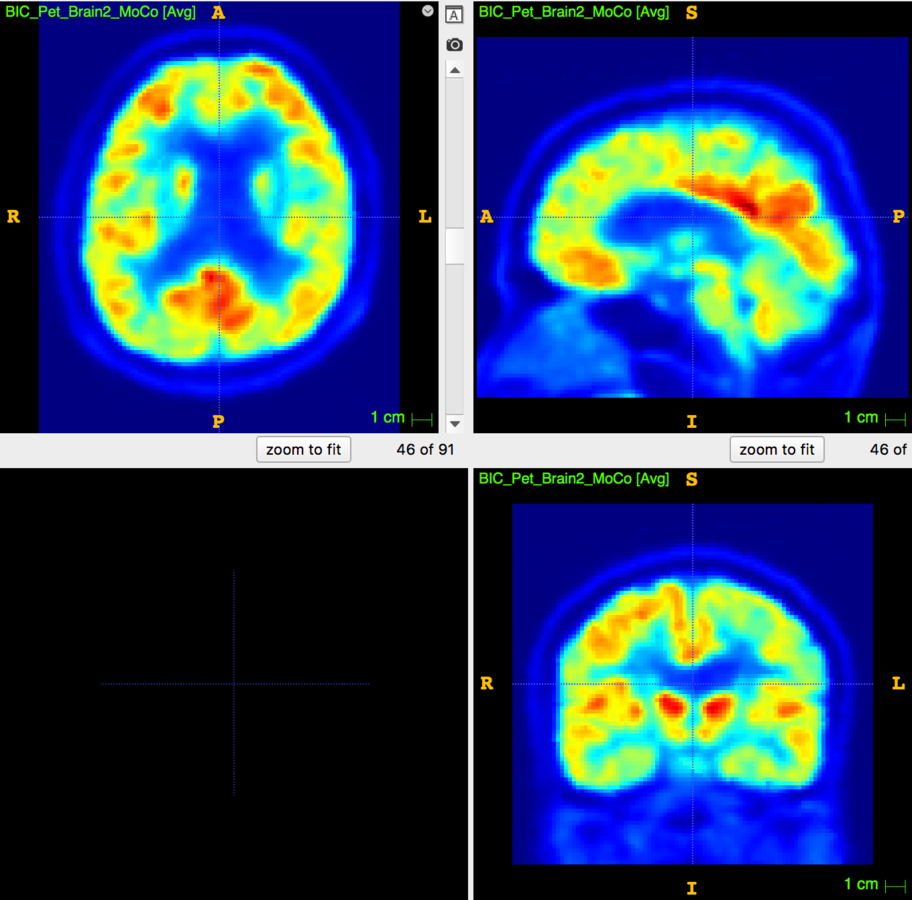
Motion Correction

Correction

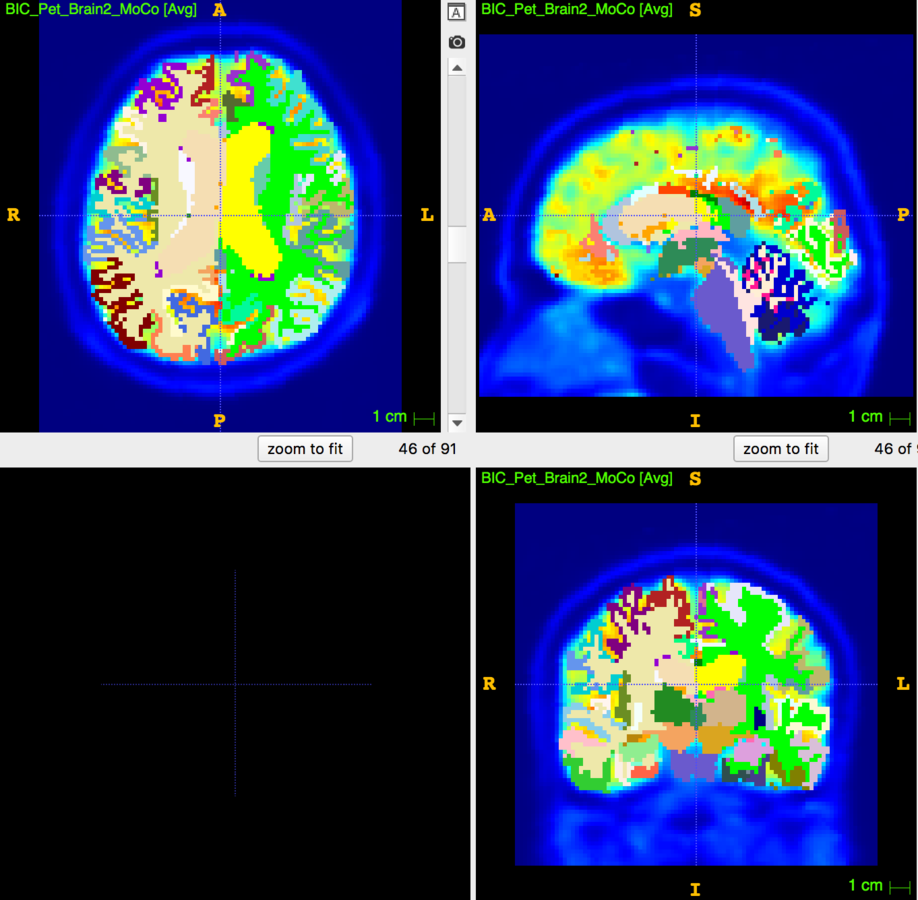
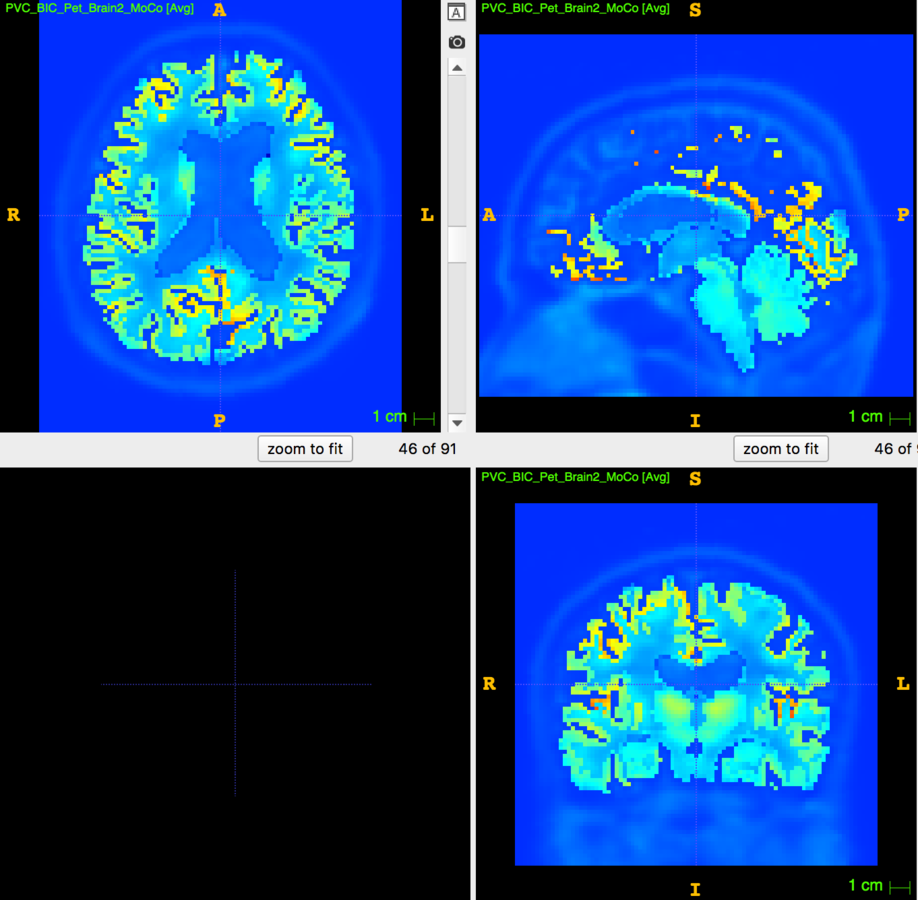
Partial Volume Correction

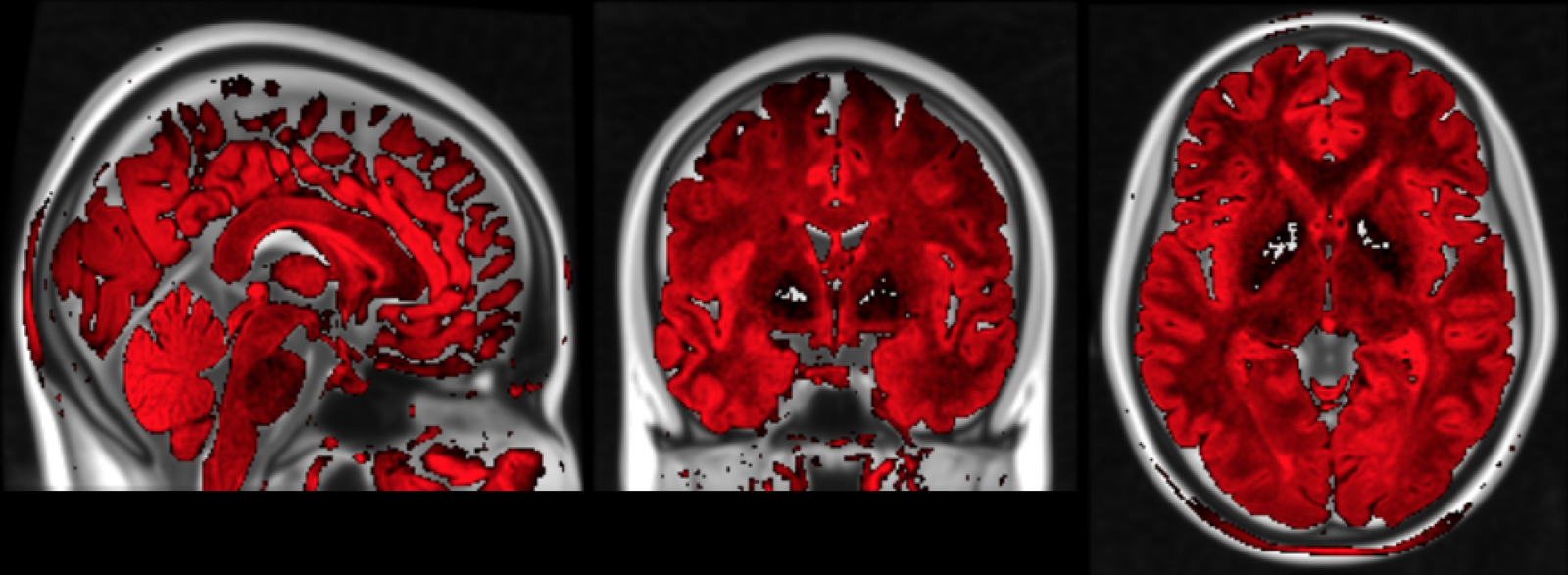
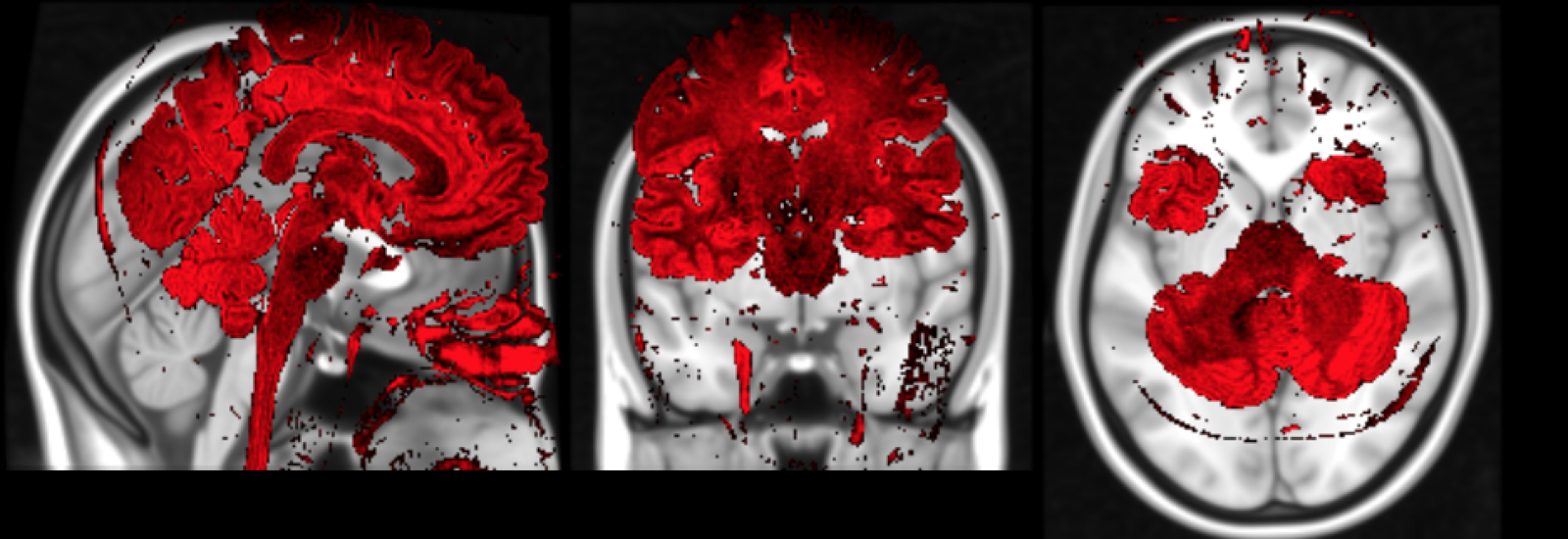
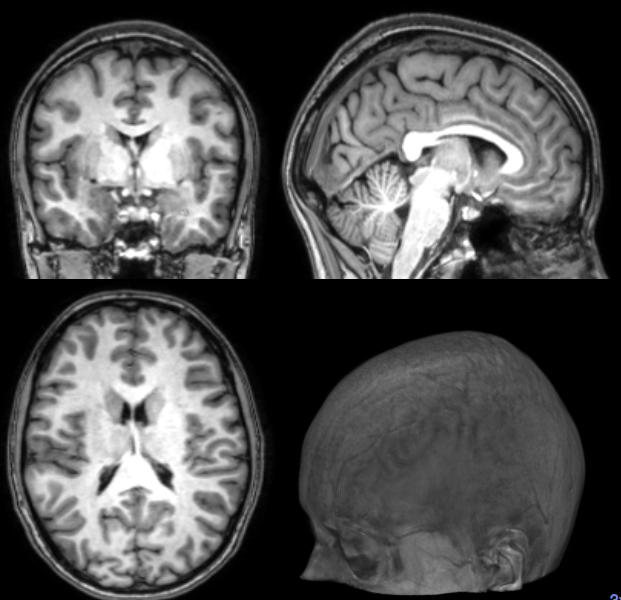
Segmentation

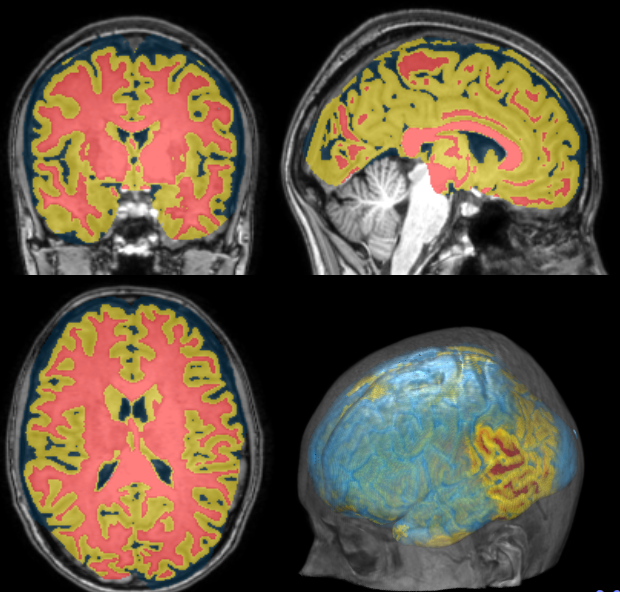
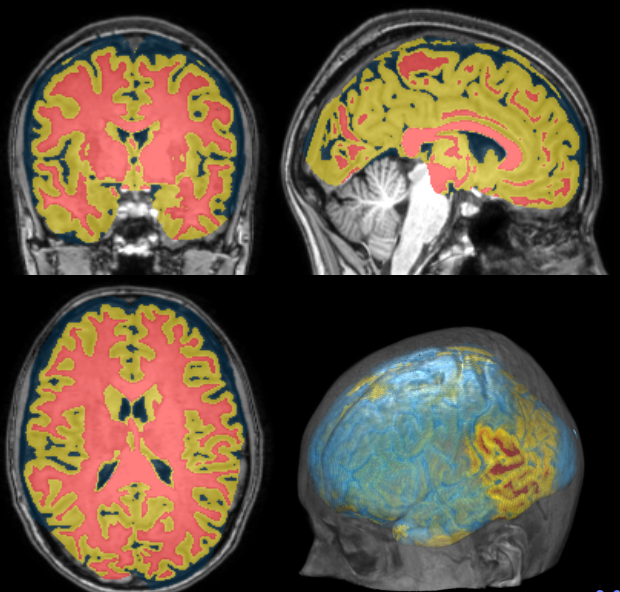
Measurements

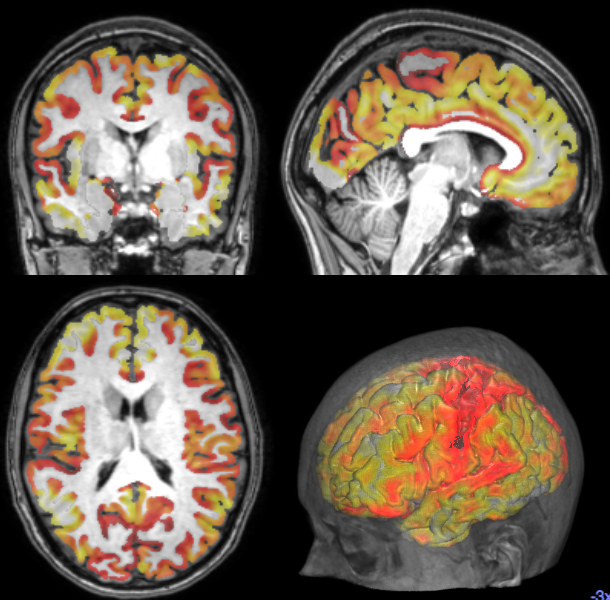
Cortical Thickness Estimation

Pipelining

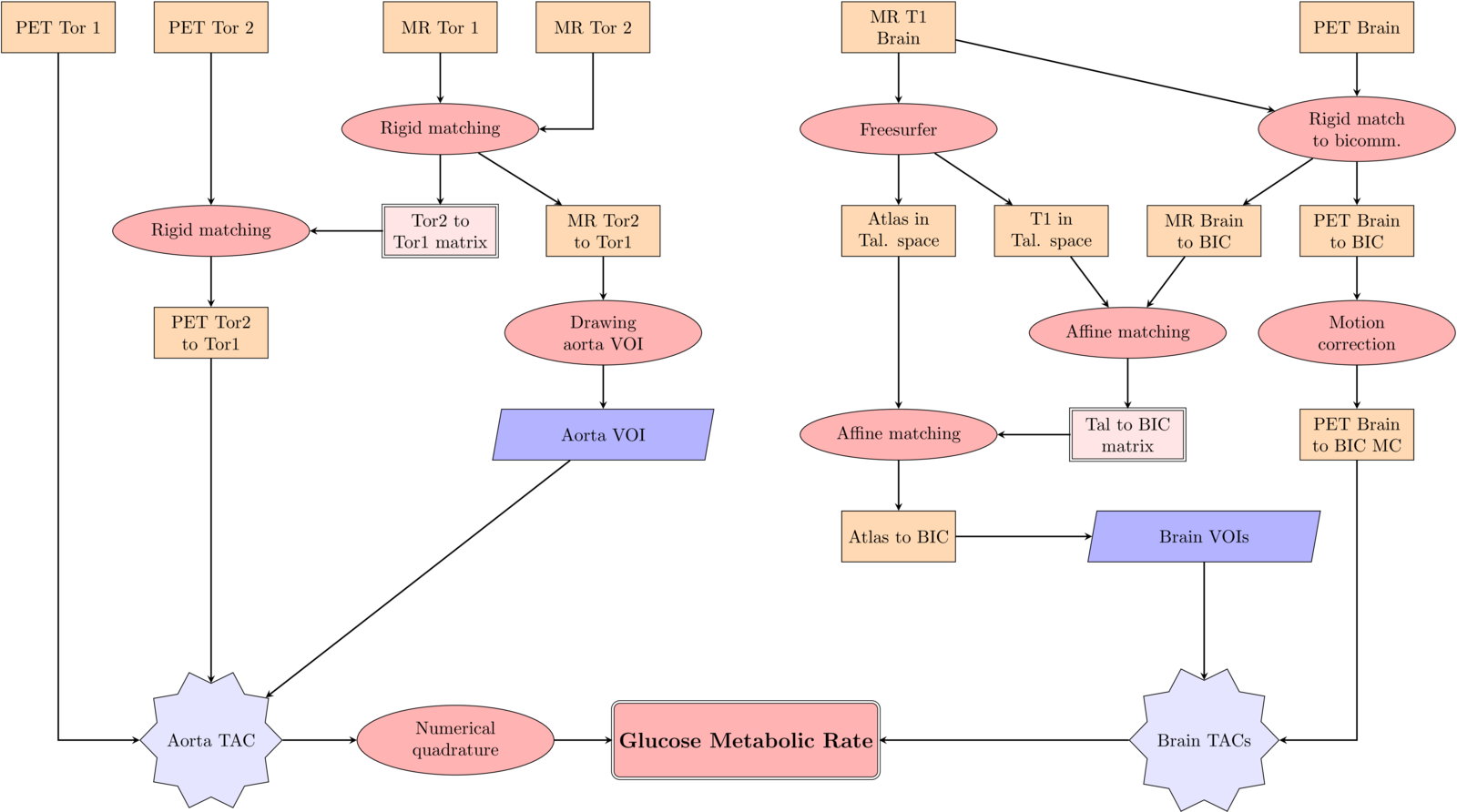
3. Image Registration

What are we doing?

where D is an appropriate distance (or pseudo-distance).

Say that the image I is represented by a function

I : \Omega \subseteq \mathbb{R}^3 \longrightarrow \mathbb{R}
I:Ω⊆R3⟶RI : \Omega \subseteq \mathbb{R}^3 \longrightarrow \mathbb{R}

and the reference image is R we look for a function

f:\mathbb{R}^3\longrightarrow \mathbb{R}^3
f:R3⟶R3f:\mathbb{R}^3\longrightarrow \mathbb{R}^3
\arg\min_{f} \mathcal{D}[I(f(x)),R(x)]
argminfD[I(f(x)),R(x)]\arg\min_{f} \mathcal{D}[I(f(x)),R(x)]

such that

Considering linear tranformation

f(x)=A⋅x+b

DOF Geom.meaning A det(A)
3 traslation Identity 1
6 rototranslation R s.t. det(R)=1 1
7 homothety aR, a>0 a
9 similitude diag(a,b,c)⋅R abc
12 affinity any s.t. det(R)≠0 ≠0

The optimal transformation is found iteratively

Otherwise the transformation is called nonlinear

Speed it up

A good way of improving the convergence of this iterative method is to downsample the input image by a factor n and use the matrix as a initial guess for the next step.

# sample python code
# input image I, reference R
# functions `register' and `apply' are user-defined

from skimage.transform import downscale_local_mean

for in n [4,3,2,1]:
    II=downscale_local_mean(I,(n,n,n))
    I_out,mat_out=register(II,R,"affine",maxit=50,tol=1.e-5)
    I=apply(mat_out,I)

In python

One can use wrappers (as nipype)...but there is a pure-python registration routine inside nipy!

import numpy as np
import nibabel as nib
import nipy.algorithms.registration as nar
import sys

in_path=sys.argv[1]; ref_path=sys.argv[2]
IN=nib.load(in_path); REF=nib.load(ref_path)

#registration initialization
register_obj = nar.HistogramRegistration(from_img = IN, to_img = REF,\
    similarity='crl1',interp=tri,renormalize=True)

#compute the optimal tranformation
transform = register_obj.optimize('affine', optimizer='bfgs',xtol = 1e-4,\
    ftol = 1e-4,gtol = 1e-4,maxiter= 70)

#apply it
resampled = nar.resample(IN, transform, OUT)

#output the result
New=nib.Nifti1Image(resampled,header=IN.header,affine=REF.affine)
nib.save(New,sys.argv[3])

Some funny example

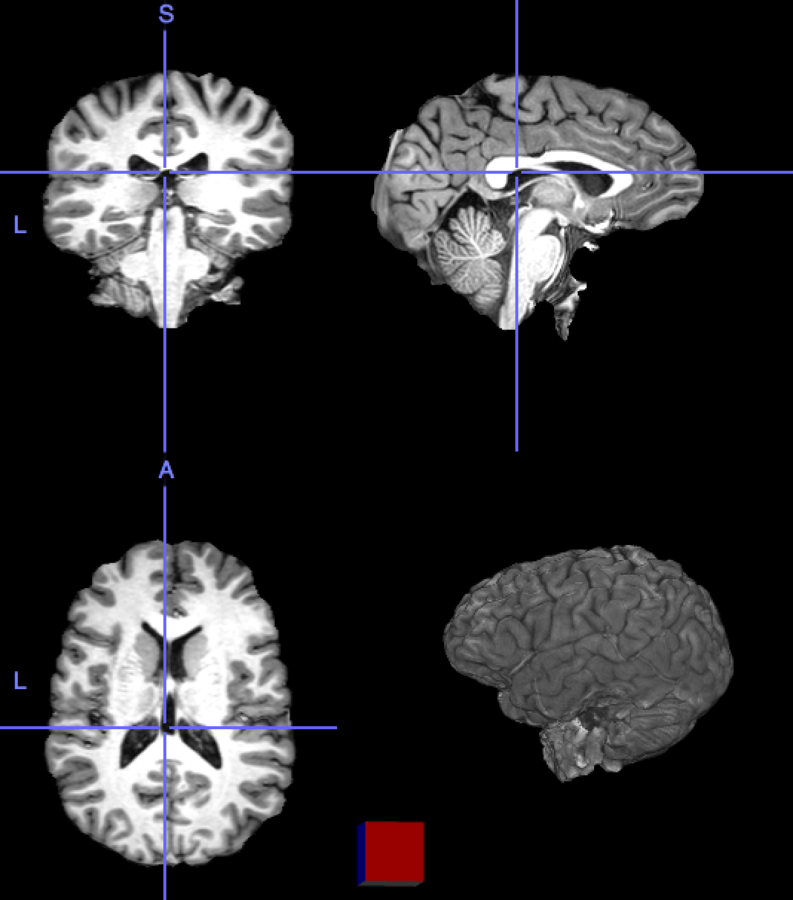
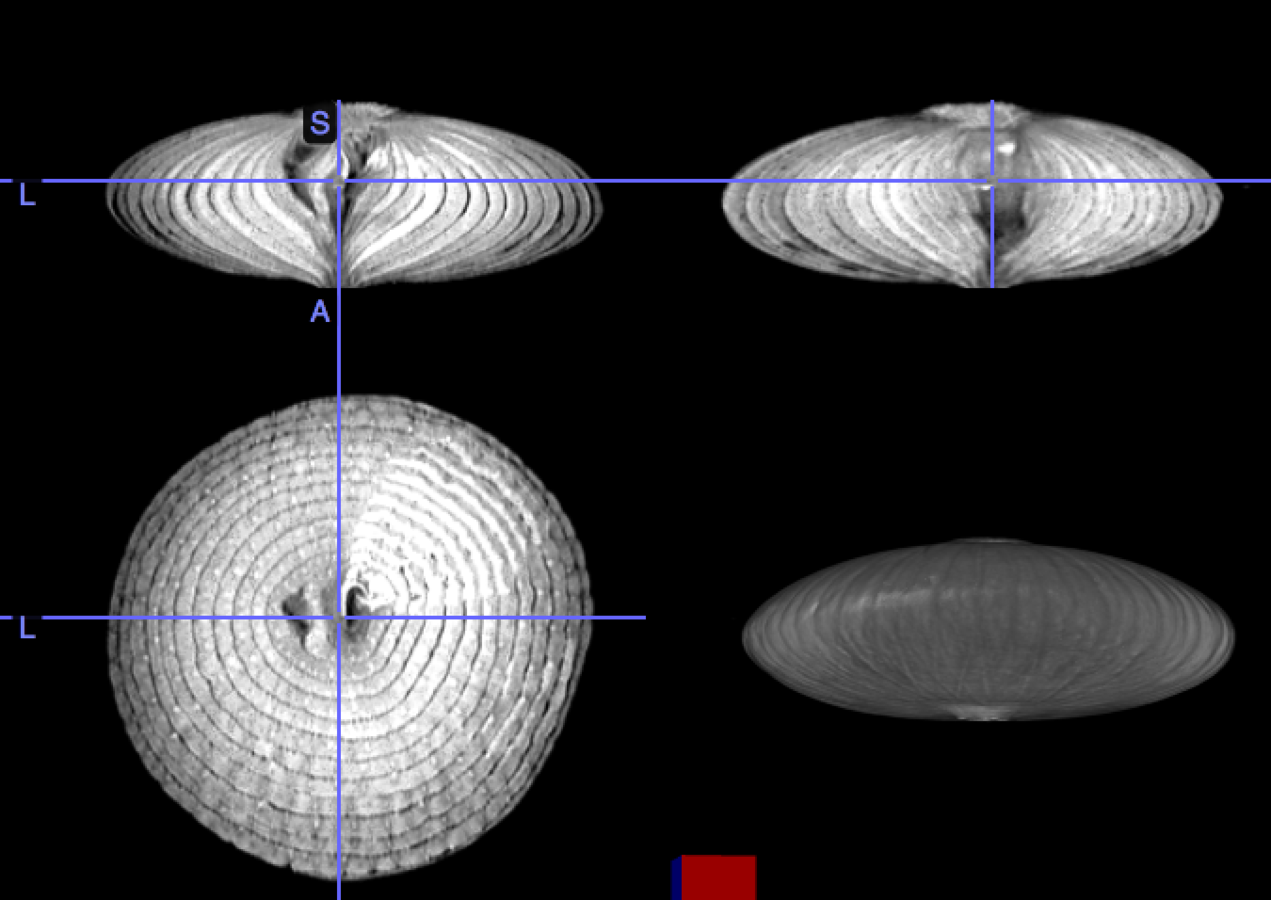
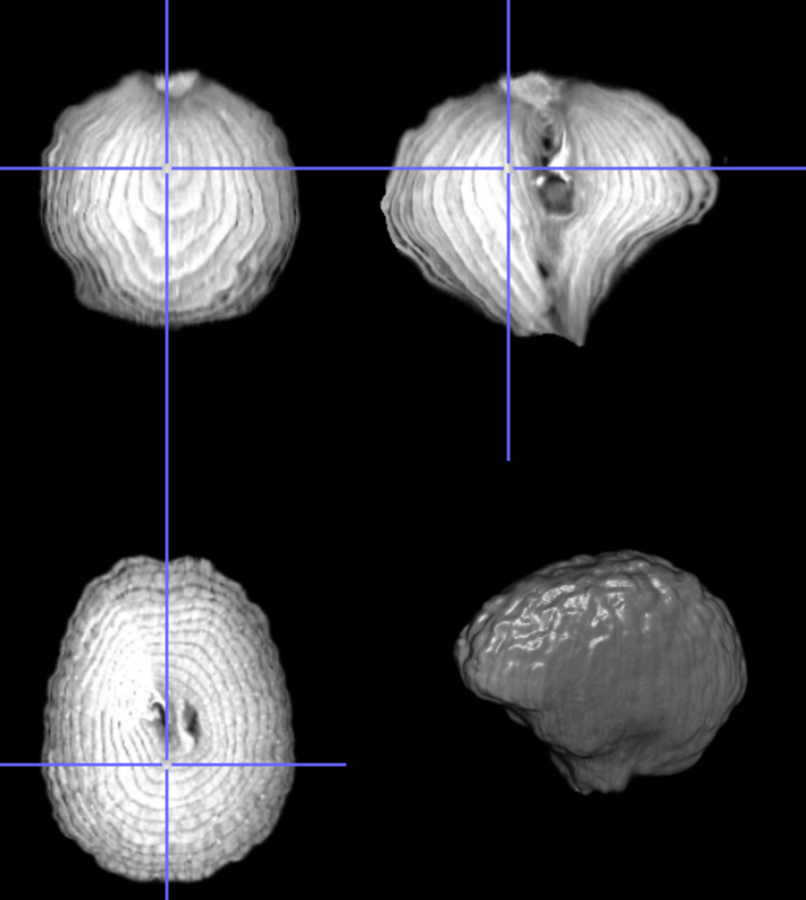
My brain is the reference, the onion the input image

Rigid transformation

Affine transformation

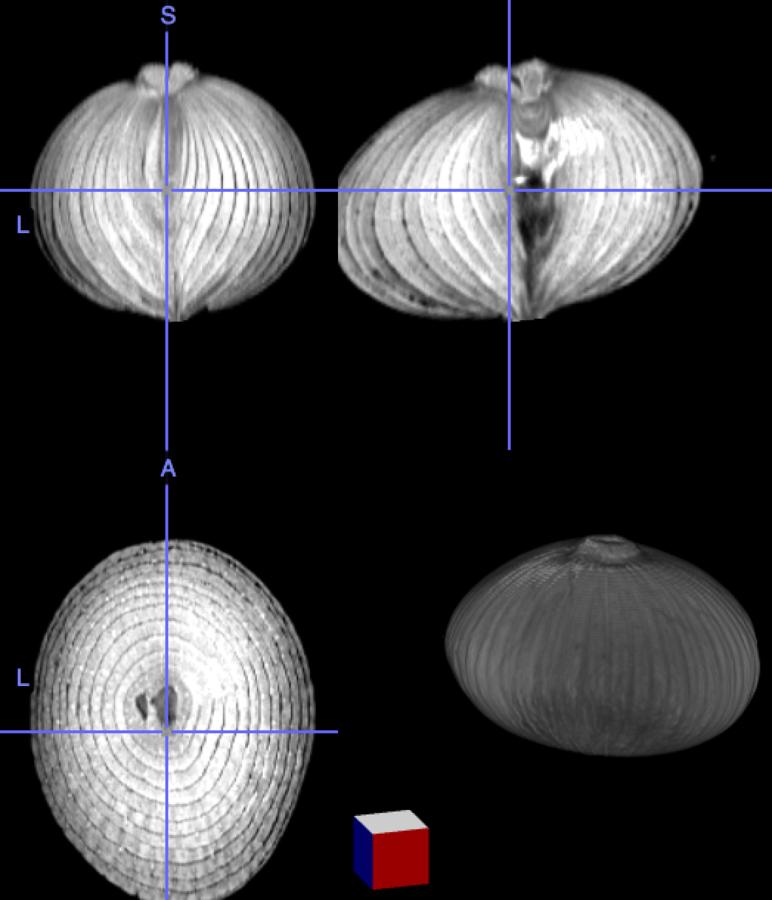
Nonlinear transformation

4. Patlak plot in PET/MRI

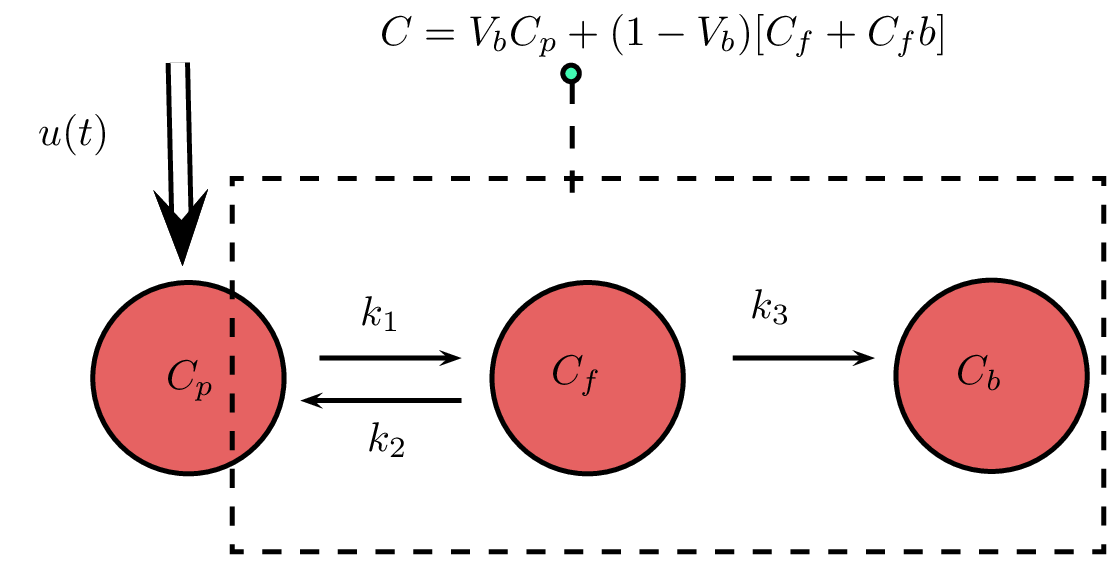
Sokoloff model for 18F-Fdg PET

Patlak plot method:

\frac{C(t)}{C_p(t)}=K \frac{\int_{0}^{t}C_p (\tau)\,d\tau}{C_p(t)} + V_b
C(t)Cp(t)=K∫0tCp(τ)dτCp(t)+Vb\frac{C(t)}{C_p(t)}=K \frac{\int_{0}^{t}C_p (\tau)\,d\tau}{C_p(t)} + V_b
K=\frac{k_{1}k_{3}}{k_{2}+k_{3}}
K=k1k3k2+k3K=\frac{k_{1}k_{3}}{k_{2}+k_{3}}

 is proportional to the absolute Metabolic Rate

We can find K by linear fit

y=K x + b
y=Kx+by=K x + b

Speed it up

In the case of voxel-based Patlak, if you think about computing the result for each voxel in a (say) 128x128x128 image

for i in voxel:
    C,Cp,int_Cp=get_counts_voxel(i)
    X=int_Cp/Cp
    Y=C/Cp
    slope, intercept, r_value, p_value, std_err = stats.linregress(np.array(XX),np.array(YY))

You are going to have a bad time...

Solution: exploit the closed form of linear regression

\left( X , 1 \right) \cdot \left( \begin{array}{c} K \\ V_b \end{array} \right)=Y
(X,1)⋅(KVb)=Y\left( X , 1 \right) \cdot \left( \begin{array}{c} K \\ V_b \end{array} \right)=Y

Normal equations are

\left(\begin{array}{c c} X \cdot X^T & sum(X)\\ sum(X) & n \end{array} \right) \left(\begin{array}{c} K \\ V_b \end{array} \right) = \left(\begin{array}{c} X \cdot Y^t\\ sum(Y)\end{array} \right)
(X⋅XTsum(X)sum(X)n)(KVb)=(X⋅Ytsum(Y))\left(\begin{array}{c c} X \cdot X^T & sum(X)\\ sum(X) & n \end{array} \right) \left(\begin{array}{c} K \\ V_b \end{array} \right) = \left(\begin{array}{c} X \cdot Y^t\\ sum(Y)\end{array} \right)

The solution of the system is

K = \frac{n X\cdot Y^T - sum(X)sum(Y)}{n X\cdot X^T - sum(X)sum(X)}
K=nX⋅YT−sum(X)sum(Y)nX⋅XT−sum(X)sum(X)K = \frac{n X\cdot Y^T - sum(X)sum(Y)}{n X\cdot X^T - sum(X)sum(X)}
V_b = \frac{sum(X)}{n} - K \frac{sum(Y)}{n}
Vb=sum(X)n−Ksum(Y)nV_b = \frac{sum(X)}{n} - K \frac{sum(Y)}{n}

Which can be also applied if Y is a matrix containing all the voxel values over the time!

This will speed up the algorithm as the matrix multiplication is implemented in parallel in numpy

for i in voxel:
    C,Cp,int_Cp=get_counts_voxel(i)
    #save in matrix Y, X is a vector
    Y[:i]=C/Cp
X=int_Cp/Cp
n=X.shape[0]
Slope=(n*np.dot(XX,YY.T)-np.sum(XX)*np.sum(YY,1))/
        (n*np.dot(XX,XX.T)-np.sum(XX)*np.sum(XX))
Intercept=(np.sum(YY,1)/n)-Slope*(np.sum(XX/n))

In python:

before:

after:

for i in voxel:
    C,Cp,int_Cp=get_counts_voxel(i)
    X=int_Cp/Cp
    Y=C/Cp
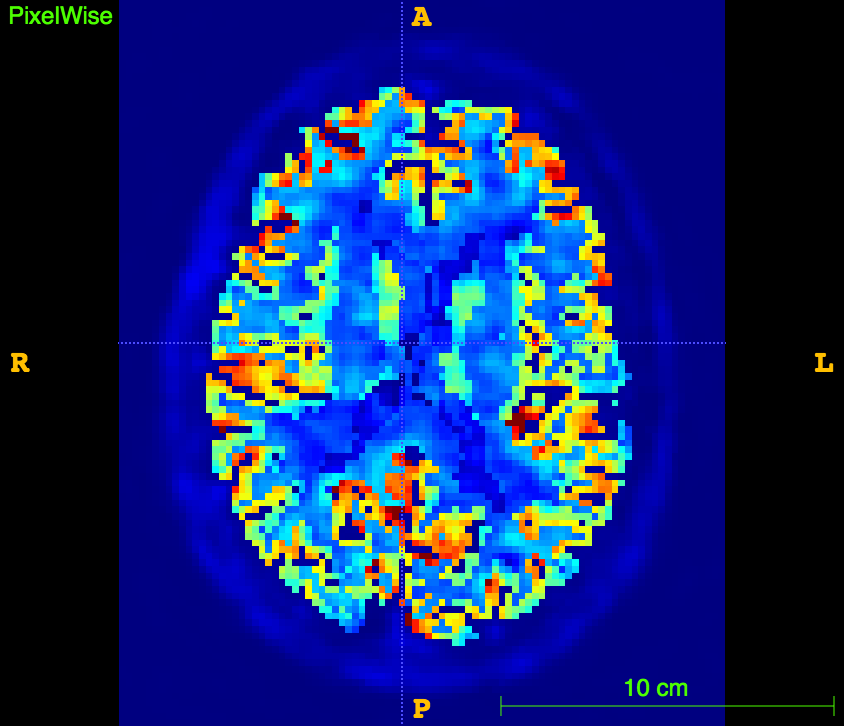
    slope, intercept, r_value, p_value, std_err = stats.linregress(np.array(XX),np.array(YY))

The resulting image

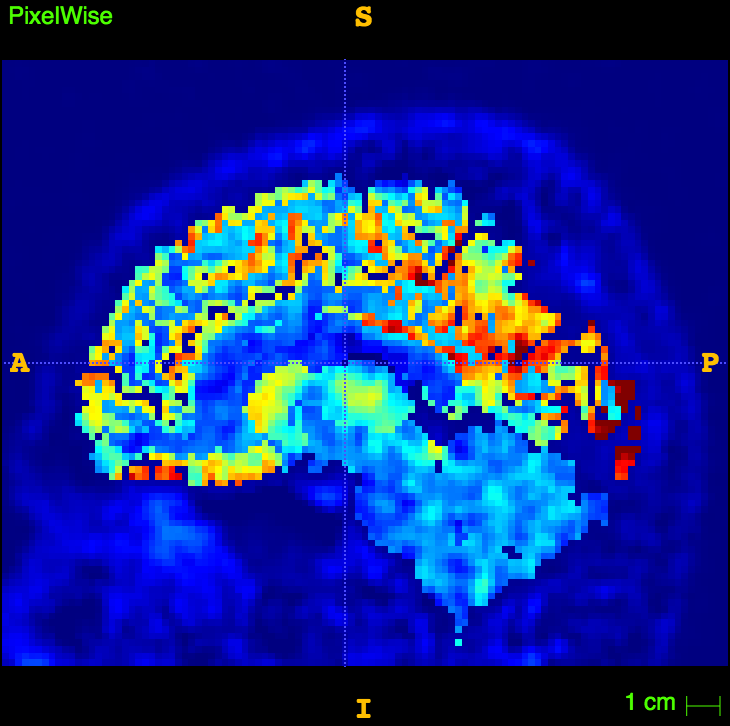
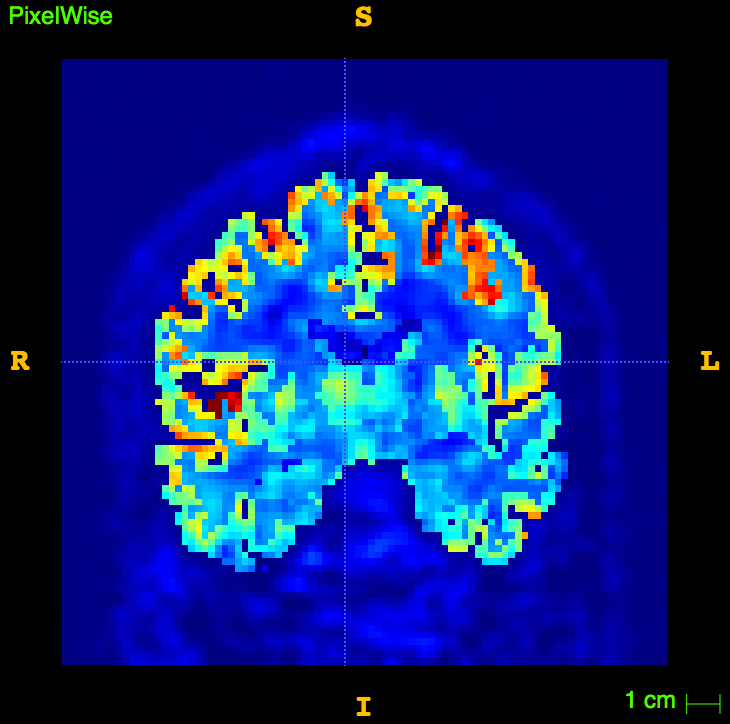
Thanks to....

MS Centre Padova

Nuclear Medicine Padova

Neurology Padova

Neuroradiology Unit Padova

 

all patients of course and...

... this audience for the attention!

Some References

  • C Cobelli, D Foster, G Toffolo,Tracer kinetics in biomedical research, Springer, 2001.
  • SR Das, BB Avants, M Grossman, JC Gee, Registration based cortical thickness measurement, Neuroimage. 2009
  • CL Epstein, ntroduction to the mathematics of Medical Imaging, Second Edition, Siam, 2008

  • TG Feeman, The mathematics of medical imaging: A beginners guide, Springer, 2010

  • ME Juweid, OS Hoekstra, Positron Emission Tomography, Humana Press, 2011.
  • CS Patlak, RG Blasberg, Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data. Generalizations, Journal of Cerebral Blood Flow and Metabolism, 1985.
Made with Slides.com