Gibbs Effect in Medical Imaging (and how to possibly reduce it)


Davide Poggiali (PNC)
In coll. w/: Stefano De Marchi
Diego Cecchin (DIMED),
Cristina Campi (DIMA - UniGE).
Numlab seminars - June 7, 2021
Summary:
- Motivation
- Interpolation for image resampling
- Bounding the error
- Gibbs Effect in image resampling
- Future works
1. Motivation: Sampling problem in PET/MRI
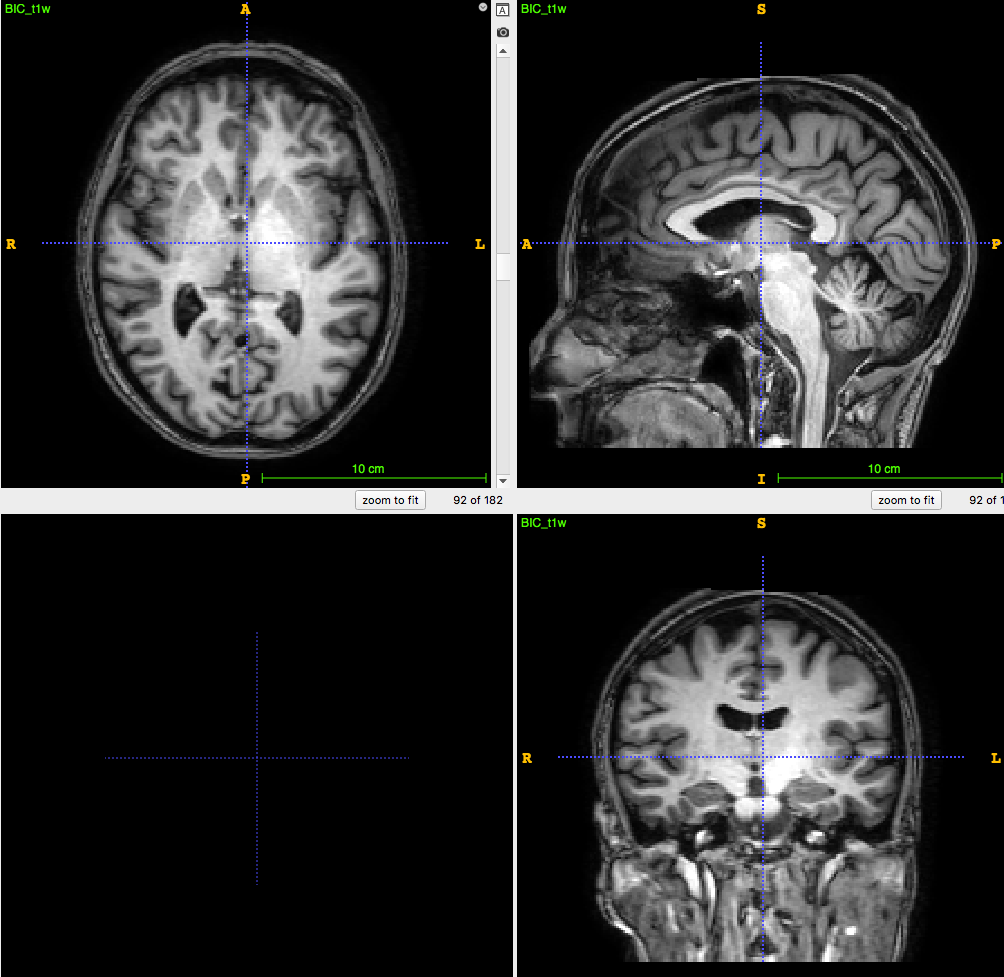
3D T1-weighted MRI:
usually ~1 mm \(^3\) voxel
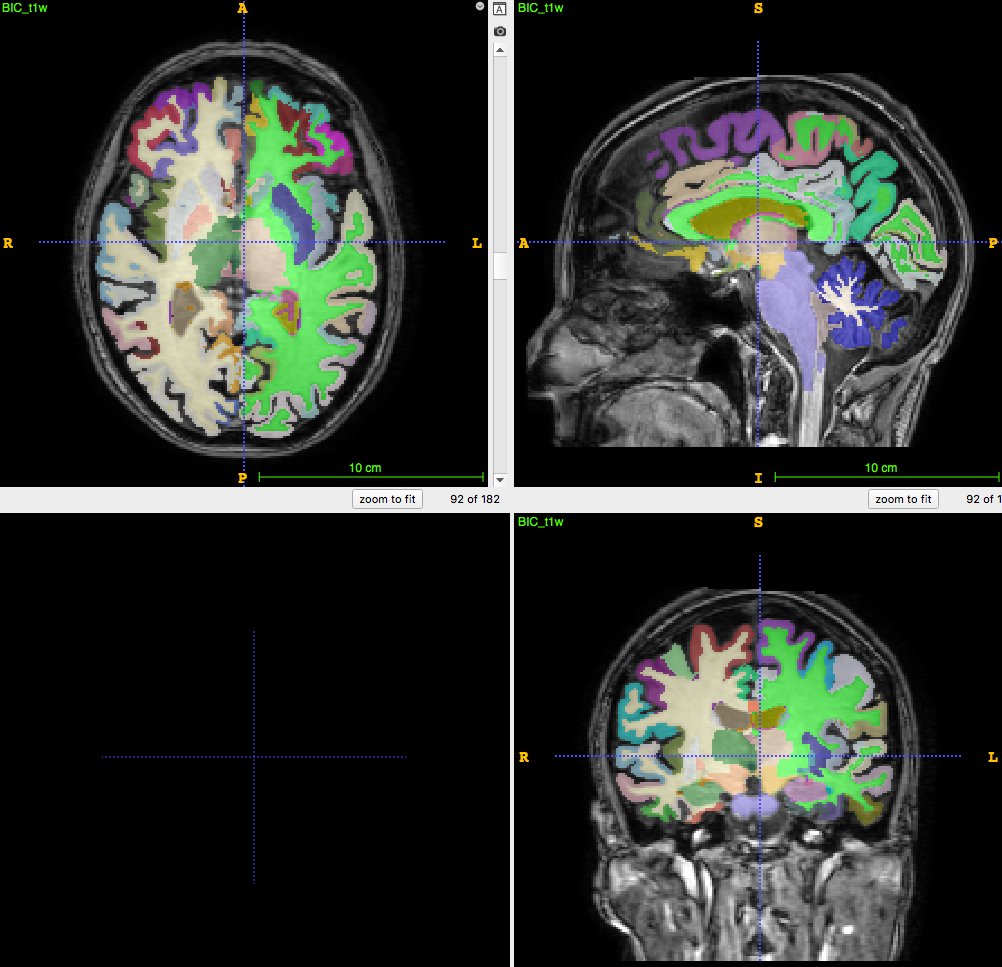
Segmentation/parcellation at full resolution
PET image:
usually ~8mm \(^3\) voxel
How to apply segmentation?
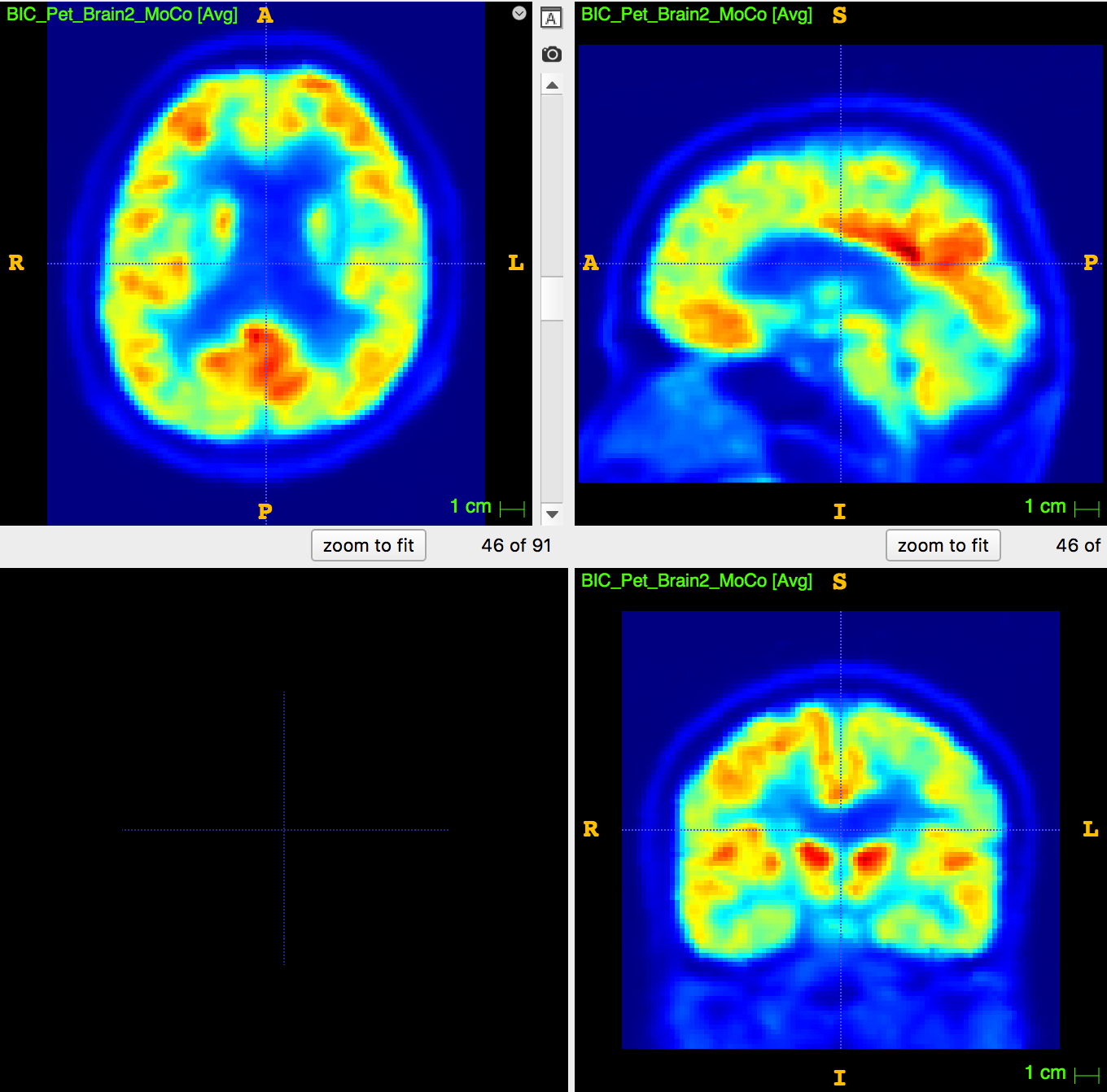
1. Undersampling T1 segmentation
2. Upsampling PET image
3. PET segmentation (no MRI)
Sampling problem in PET/MRI
In silico test: Shepp-Logan 3D Phantom
Using a phantom the gold standard is known and we can analyse the errors of approximation.
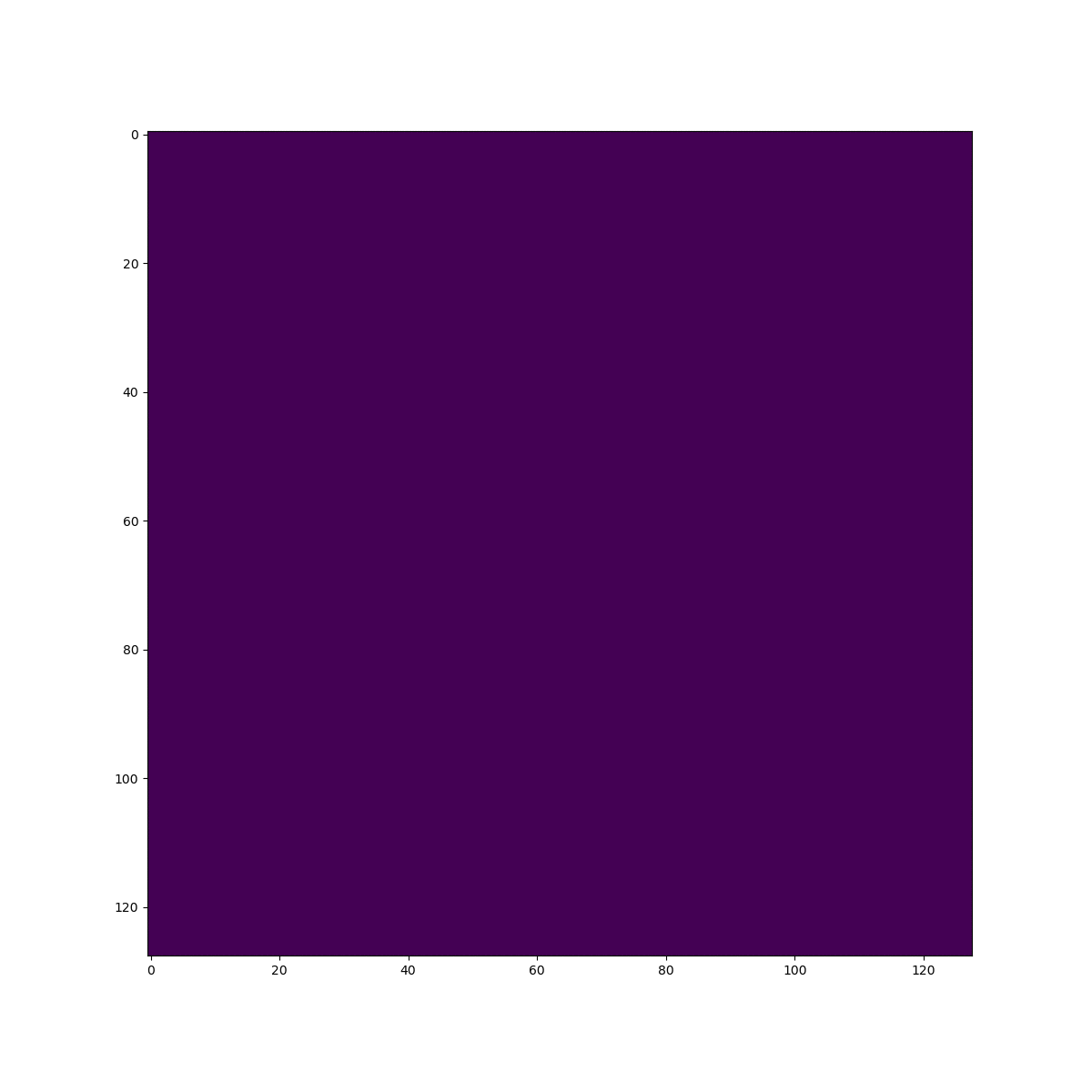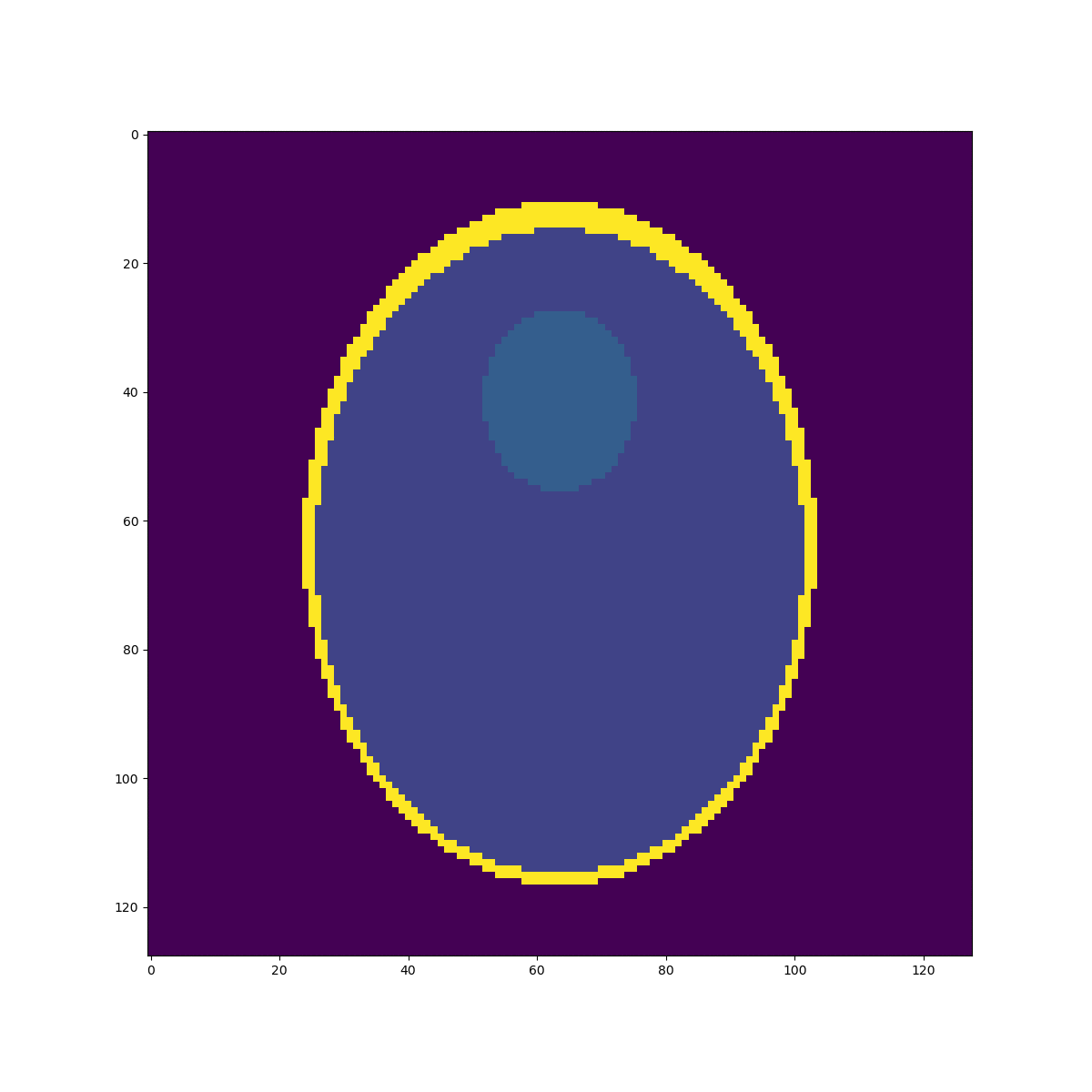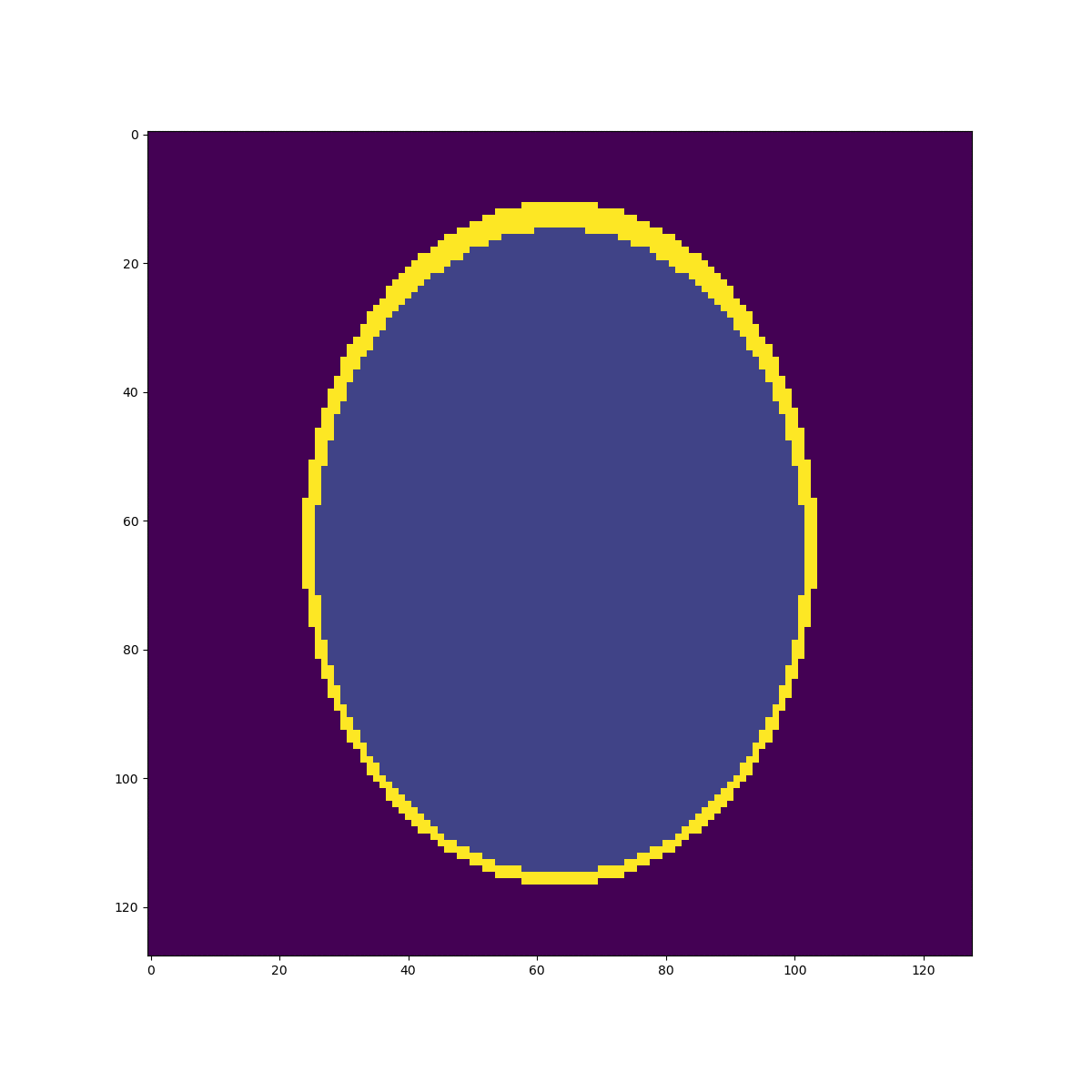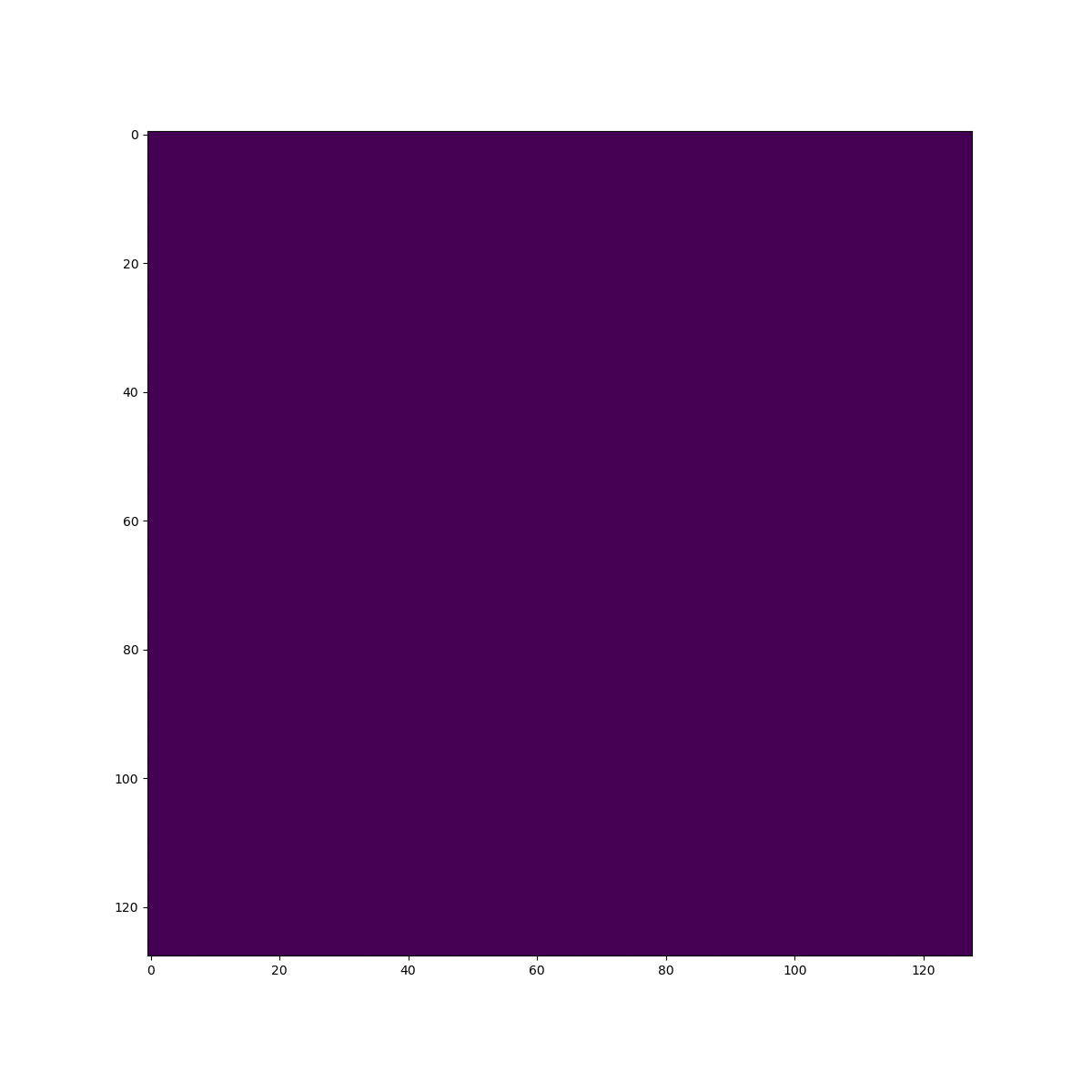
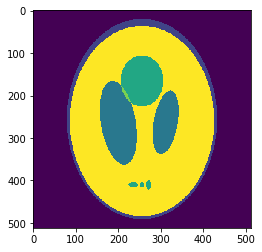
High resolution "morphological" image
Segmentation mask
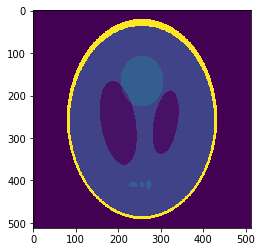
Low resolution "functional" image
Resampling is performed in ANTs
Original values at masks (gold standard):
g=[0.0, 1.0, 0.05, 0.3, 0.15, 0.2]
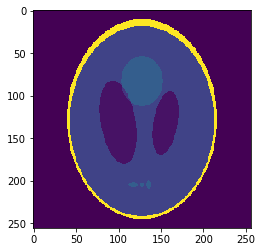
Downsampled segmentation mask
Low resolution "functional" image

Undersampling segmentation
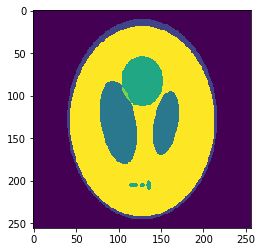
The 2-norm relative error is \(\sqrt{\sum{ (g_i-v_i)^2 \over g_i^2}}\approx 0.058\)
Sampled mean values at masks:
v =[0.00033, 0.937, 0.0523, 0.298, 0.153, 0.206]
Oversampled "functional" image
Oversampling functional image
The 2-norm relative error is ~\(0.103\)
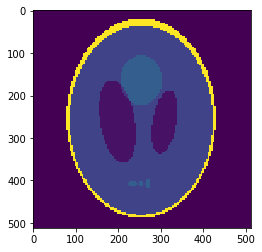

Segmentation mask
Sampled mean values at masks:
v=[0.0015, 0.889, 0.054, 0.297, 0.158, 0.209]
If we look at the pointwise interpolation error


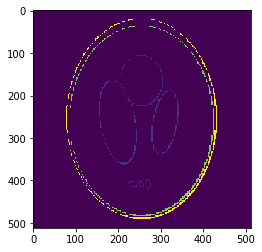
We can observe it is mostly higher distributed around the borders, where the gradient is higher.
This is what we call the Gibbs Effect...but is it systematic?
2. Interpolation for image resampling
A three-dimesional MRI can be ~ \(10^8\) voxels (256x256x256 takes ~800Mb in double precision, uncompressed) and counting. Hence a fast, lightweight interpolation method is needed.
Q: What is the fastest interpolation method?
R: When the interpolation and evaluation nodes coincide 😛😛😛😛
2. Interpolation for image resampling
Let us take a \(10^8\) voxels image. The interpolation matrix would be \(10^8 \times 10^8\) .... ~80Pb in double precision!
What is the fastest (nontrivial) interpolation method?
- Choose a basis;
- Compute Interpolation/Evaluation matrices;
- Solve a linear system;
- Multiply Eval. matrix by coefficients.
2. Interpolation for image resampling
So we need to choose a basis:
- Separable → the interpolation is computed on each axis sequentially;
- Cardinal → no need to compute or invert the Interpolation matrix;
- Compact supported → Evaluation matrix is sparse.
To achieve that we have to suppose that the interpolation nodes are on a equispaced grid.
2. Interpolation for image resampling
[Step I] Let \(\omega_a: \mathbb{R}_+ \to \mathbb{R}\), with \(a\in\mathbb{N}\) the support radius, a function such that:
- \(\omega_a(0) = 1\);
- \(\omega_a(k) = 0\;\; \forall~ k \in \mathbb{N}\setminus \{0\}\);
- \(\omega_a(r) = 0\;\;\forall~ r \geq a\).

2. Interpolation for image resampling
[Step II] Let \(\{t_i\}\), a set of \(N\) equispaced points of the interval \([\alpha, \beta]\). Then we define for the univariate basis
\[ w_{\sigma}(t - t_i)=\frac{\omega_a(\sigma|t-t_i|)}{\sum_{j=0}^N \omega_a(\sigma |t-t_j|)},\]
with \(\sigma = \frac{N}{\beta-\alpha}\) a scaling factor.
2. Interpolation for image resampling
[Step III] The three-variate interpolant is
\[\mathcal{P}_f (\bm{x}) = \sum_{ijk} f(\bm{x}_{ijk})W_{ijk}(\bm{x})\]
with
\[W_{ijk}(x, y, z) = w_{\sigma_1}(x-x_i)\; w_{\sigma_2}(y-y_i) \;w_{\sigma_3}(z-z_i)\]
the separable basis. This basis is also:
- Cardinal;
- Compact supported;
- Radial in each component.
This is called interpolation by convolution.
3. Bonding with the error
Being the basis separable we can consider univariate interpolation
Let us suppose without loss of generality that the function
\[f:[0,1] \to \mathbb{R}\]
is known at \(x_i = \frac{i}{N},\;\;i=0,\ldots,N\).
By using a function \(\omega_a(r)\) satisfying (I), we define the interpolating function
\[ \mathcal{P}^N_f(x) = \sum_{i=0}^N w(x-x_i) f(x_i)\]
with \(w(t - t_i) = \frac{\omega_a(\frac{1}{N}|t-t_i|)}{\sum_{j=0}^N \omega_a(\frac{1}{N} |t-t_j|)}\).
3. Bonding with the error
Lemma: Suppose that \(x\in (x_k, x_{k+1})\) for some \(k\in 0, \ldots, N-1\) and that the support radius is \(a\in\mathbb{N}\).
Then
$$\mathcal{P}^N_f(x) = \sum_{i=\max(0, k-a)}^{\min(N, k+a-1)} w(x-x_i) f(x_i).$$
3. Bonding with the error
Theorem [Pointwise error bound]: If the interpolation point \(x\in(x_k, x_{k+1})\) with \(a\leq k \leq N-a+1\) and \(m_{w}>0\), then
\[|\mathcal{P}^N_f (x) - f(x)| \leq \frac{M_{w}}{m_{w}} \sum_{i=k-a}^{k+a-1} |f(x) - f(x_i)|.\]
Once calculated
\[M_{w} = \max_{x\in [0,1]} \left| \omega_a(N|x-x_i|)\right|,\;\;\text{and}\]
\[m_{w} = \min_{x\in [0,1]} \left|\sum_{j=0}^N \omega_a(N|x-x_j|) \right|\]
we can formulate
3. Bonding with the error

4. Gibbs effect in Image Resampling
Gibbs effect (in a nutshell):
- Appears at discontinuities as oscillatory;
- Does not vanish as \(N\to\infty\);
- As \(N\to\infty\) their frequency grows, the amplitude reaches a plateau.
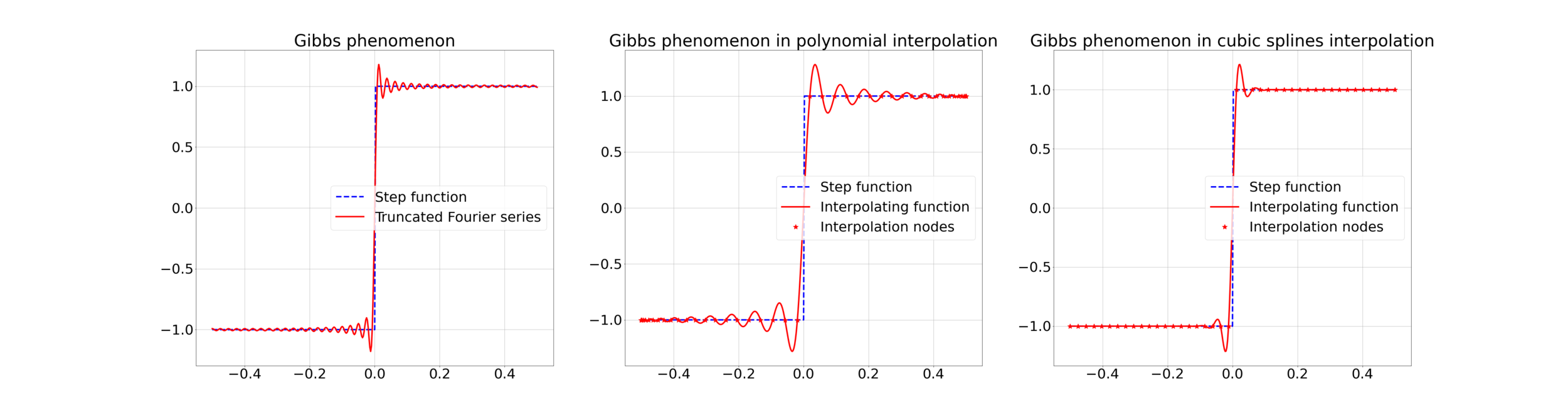
4. Gibbs effect in Image Resampling
Gibbs effect is called "ringing effect" in MRI.
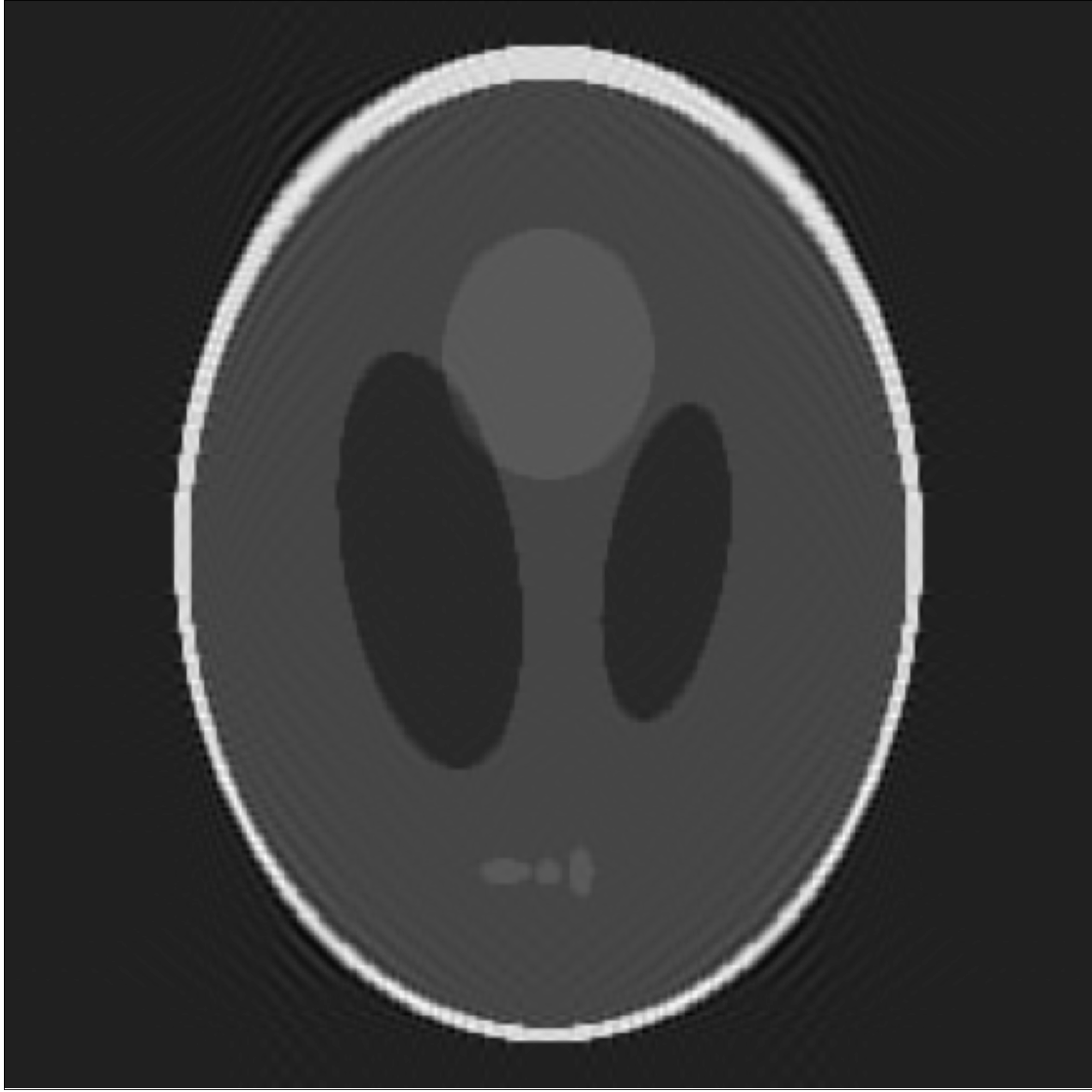
4. Gibbs effect in Image Resampling
Corollary 1: if \(f\) is continuous in \(x\in[0,1]\), then
\[\lim_{N\to\infty} |\mathcal{P}^N_f (x) - f(x)| = 0 .\]
Corollary 2: if \(f\) is discontinuous at \(x\in[0,1]\), and the limit of the error exists, then
\[0 \leq \lim_{N\to\infty} |\mathcal{P}^N_f (x) - f(x)| \leq a\frac{M_{w}}{m_{w}} |f(x^-) - f(x^+)| .\]
4. Gibbs effect in Image Resampling
Corollary 3: if \(f\) is bounded and discontinuous at \(\xi\), \(x\in (x_k, x_{k+1})\) and \(\xi \in [x_{k+p}, x_{k+p+1}]\) with \(p \in\{ -a, \ldots, a-2\}\), calling
\[ F = \sum_{k-a}^{k+a-1}|f(x)- f(x_i)|,\]
- Case 1: \(\xi\leq x\) (i.e. \(p\leq 0\)): \[pc_1 + c_2 \leq F \leq pC_1 + C_2\] \(c_1, C_1>0\)
- Case 2: \(\xi> x\) (i.e. \(p> 0\)): \[pr_1 + r_2 \leq F \leq pR_1 + R_2\]
\(r_1, R_1<0\).
5. Future works
An approach based on Fake Nodes approach (FNA) is currently being evaluated.
PROs:
- It is a "natural choice", since the segmentation map offers precious informations at higher resolution;
- it is relatively easy to implement on top on any interpolation method;
- some variant can be easily written in case of a probabilistic segmentation.
CONs:
- A discontinuity-informed mapping does not naturally map an equispaced grid to an equispaced grid;
- the effect of segmentation errors to FNA is currently unknown.
References
[1] Burger, W.; Burge, M.J., Principles of digital image processing: core algorithms; Springer, 2009.
[2] Dumitrescu.; Boiangiu. A Study of Image Upsampling and Downsampling Filters. Computers doi:10.3390/computers8020030.4139
[3] S. De Marchi, F. Marchetti, E. Perracchione, Jumping with Variably Scaled Discontinuous Kernels (VSDKs), BIT Numerical Mathematics 2019.
[4] S. De Marchi, F. Marchetti, E. Perracchione, D. Poggiali, Polynomial interpolation via mapped bases without resampling, JCAM 2020.
[5] S. De Marchi, F. Marchetti, E. Perracchione, D. Poggiali, Multivariate approximation at Fake Nodes, AMC 2021.
[5] S. De Marchi, G. Elefante, E. Perracchione, D. Poggiali, Quadrature at Fake Nodes, DRNA 2021.
[6] C. Runge, Uber empirische Funktionen und die Interpolation zwischen aquidistanten Ordinaten, Zeit. Math. Phys, 1901.
Thank you!