Insegnare la matematica con Python: percorsi suggeriti per le Scuole Superiori

Davide Poggiali

postDoc fellow

PyCon9 Firenze,

venerdì 20 aprile 2018

Mi chiamo Davide, sono assegnista di ricerca nel Dipartimento di Matematica, Università di Padova.

Nel 2017 ho svolto alcune supplenze nelle Scuole Superiori, e ho cominciato a usare Python come supporto integrativo per alcuni moduli didattici.

twitter: @Dav1d3P0g

Python può essere un valido strumento di aiuto didattico:

Gli studenti vedono applicati i concetti appena appresi sullo schermo.
L'insegnante riesce con semplici righe di codice ad evidenziare i concetti-chiave.
Alcuni degli studenti si appassionano alla materia, trovando nella programmazione uno sbocco "naturale" alle proprie inclinazioni.
La materia guadagna in concretezza agli occhi degli studenti.

Ci sono anche dei rischi da scongiurare nell'uso del calcolatore:

Alcuni studenti possono vedere il computer come "macchina-che-fa-i-compiti-al-posto-mio".
Il termine "nativi digitali" è ingannevole: gli studenti non nascono con una "consapevolezza informatica" nelle vene.

Argomenti trattati

Insiemi e logica.
Monomi e polinomi.
Geometria cartesiana (punti, rette).
Coniche.
Sistemi di equazioni lineari.

Per ogni argomento vedremo:

Un'introduzione alla librerie in uso.
Comandi standard per svolgimento di esercizi.
Ridefinire per non soccombere..

1. Insiemi e logica

Python "puro" ha già un ambiente "set" che funziona come gli insiemi insegnati nelle scuole.

>{1,2,3,1,1,1,1}

set([1,2,3])

>A={a for a in "abbecedario"}
>print(A)

set(['a', 'c', 'b', 'e', 'd', 'i', 'o', 'r'])

...e inoltre cha anche gli operatori booleani True e False, con le rispettive operazioni logiche...

>not True

False

>True and True

True

>True or False

True

Ecco come fare unione, intersezione, differenza e differenza simmetrica


>A={a  for  a in  "pythonfigata"}
>B={a for a in "nonmiannoio"}
>
>#unione
>A|B

{'a', 'f', 'g', 'h', 'i', 'm', 'n', 'o', 'p', 't', 'y'}

>#intersezione
>A&B

{'a', 'i', 'n', 'o'}

>#differenze
>A-B

{'f', 'g', 'h', 'p', 't', 'y'}

>B-A

{'m'}

>#differenza simmetrica
>A^B

{'f', 'g', 'h', 'm', 'p', 't', 'y'}

Ci potremmo fermare qui....

...oppure provare ad usare le definizioni per riscrivere il codice!

A\cap B =\left\lbrace x | x\in A \;\land\; x\in B \right\rbrace

A\cup B =\left\lbrace x | x\in A \;\lor\; x\in B \right\rbrace

def intersezione(A,B):
    return {x for x in list(A)+list(B) if x in A and x in B}

def unione(A,B):
    return {x for x in list(A)+list(B) if x in A or x in B}

A - B =\left\lbrace x | x\in A \;\land \; !(x\in B) \right\rbrace

def differenza(A,B):
    return {x for x in list(A)+list(B) if x in A and not(x in B)}

def diff_simmetrica(A,B):
    return differenza(unione(A,B),intersezione(A,B))

A \Delta B =\left\lbrace x | (x\in A \;\land \; !(x\in B)) \lor (x\in B \;\land \; !(x\in A)) \right\rbrace =

= (A\cup B) - (A\cap B)

2. Monomi e polinomi.

Per parlare di monomi e polinomi è necessario introdurre il pacchetto sympy

>import sympy as s
>x, y, z = s.symbols('x y z')
>#scrivo la mia prima espressione
>a=x**3-y*x+3*x*z
>#semplici operazioni sono automatiche
>a+3*x**3

4*x**3 - x*y + 3*x*z

>#non tutto è automatico..
>a/x

(x**3 - x*y + 3*x*z)/x

>a*x

x*(x**3 - x*y + 3*x*z)

>s.simplify(a/x)

x**2 - y + 3*z

sympy è una libreria di calcolo simbolico, gli oggetti più semplici sono le espressioni algebriche

Un monomio è un'espressione algebrica costituita da un prodotto di fattori. Un polinomio la somma algebrica di monomi.

Sympy non ha un oggetto per i monomi, ma sa dire se un polinomio è monomio o no.


>a=s.Poly(3*x**2*y,x,y)
>b=s.Poly(4*x*y,x,y)
>a.is_monomial

True

>c=a+b
>c.is_monomial

False

>p=s.Poly(x**2 + y*x )
>p.coeffs()

[1, 1]

> p.degree()

 2

Di un polinomio è possibile conoscere coefficienti e grado

e inoltre si possono verificare facilmente i prodotti notevoli

>(a-b)*(a+b)==a**2 - b**2

True

>(a+b)**2==a**2+b**2

False

>(a+b)**2==a**2+2*a*b+b**2

True

La divisione fra polinomio e polinomio di grado uno può essere riscritta con Ruffini

>d=x**3-4*x-2
>n=x+1
>s.div(d,n)

(x**2 - x - 3, 1)

>def ruffini(a,b):
    for i in range(1,len(a)):
        a[i]=a[i]+a[i-1]*b
    q=a[:-1]; r=a[-1]
    return q,r
>
>ruffini([1, 0, -4,-2],-1)

([1, -1, -3], 1)

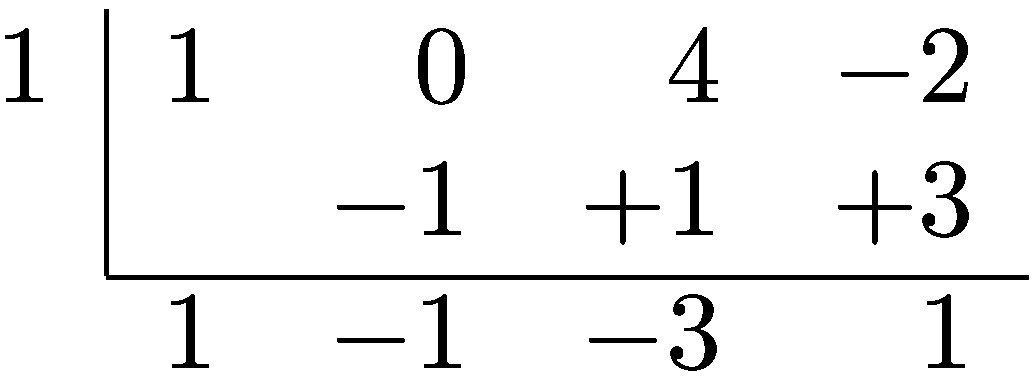
3. Geometria cartesiana.

In sympy i punti sono definiti a partire da liste 2( o 3)-dimensionali e le rette a partire da due punti o un punto e lo slope.

>A=s.Point(2,2)
>B=s.Point(4,4)
>C=s.Point(7,1)
>r=s.Line(A,B)
>r.equation()

-2*x + 2*y

>def retta(m,q):
    return s.Line(s.Point(0,q),slope=m)
>
>retta(1,1).equation()

-x + y - 1

Possiamo quindi definire per conto nostro una funzione che date slope e intercetta restituisca una retta

Inoltre possiamo riscrivere le distanze fra punti e punto retta così come le abbiamo studiate a scuola

>A=s.Point(2,2)
>B=s.Point(4,4)
>C=s.Point(7,1)
>
>r_AB=s.Line(A,B)
>r_BC=s.Line(B,C)
>r_AC=s.Line(A,C)

>#distanza punto-retta
>r_AC.distance(B)

6*sqrt(26)/13

>#per ricavare i coefficienti
>r_AB.coefficients

(-2, 2, 0)

>def dist_puntoretta(r,P):
    c=r.coefficients
    return abs(c[0]*P[0]+c[1]*P[1]+c[2])/s.sqrt(c[0]**2+c[1]**2)

>dist_puntoretta(r_AC,B)

6*sqrt(26)/13

>A.distance(B)

2*sqrt(2)

>def dist_punti(P1,P2):
    return s.sqrt((P1[0]-P2[0])**2+(P1[1]-P2[1])**2)

>dist_punti(A,B)

2*sqrt(2)

Infine possiamo scrivere una funzione che verifiche che due rette siano parallele/perpendicolari

>A=s.Point(2,2)
>B=s.Point(4,4)
>C=s.Point(7,1)
>
>r_AB=s.Line(A,B)
>r_BC=s.Line(B,C)
>r_AC=s.Line(A,C)


>def parallele(r1,r2):
    return r1.slope==r2.slope

>def perpendicolari(r1,r2):
    return r1.slope==-1./r2.slope

>perpendicolari(r_AB,r_BC)

True

>parallele(r_AB,r_AB)

True

>r_AB.is_perpendicular(r_AC)

False

>r_AB.is_perpendicular(r_BC)

True

4. Coniche

Sympy è incompleto sulle coniche:

alle parabole mancano alcune funzioni (ne scriviamo noi in classe!), non ci sono le iperboli (idea progetto scolastico?)

La parabola è definita a partire dal fuoco e dalla direttrice (orizzontale o veriticale)

>P=s.Parabola(s.Point(0,0),s.Line(s.Point(1,1),slope=0))
>P.equation()

-x**2 - 2*y + 1

Come passare dall'equazione all'oggetto sympy?

Guardo il libro di testo....

y=ax^2 +bx +c

F=\left(-\frac{b}{2a}; \frac{1-\Delta}{4a}\right)

y= -\frac{1+\Delta}{4a}

>def eq2parabola(eq):
    #qui si suppone che il coefficiente di y sia -1
    a,b,c=eq.coeff(x**2), eq.coeff(x), eq.subs(x,0).subs(y,0)
    Delta=b**2-4*a*c
    F=s.Point(-(b)/(2*a),(1-Delta)/(4*a))
    direct=s.Line(s.Point(0,-(1+Delta)/(4*a)),slope=0)
    return s.Parabola(F,direct)
>
>eq=-y+x**2-1
>eq2parabola(eq)

Parabola(Point2D(0, -3/4), Line2D(Point2D(0, -5/4), Point2D(1, -5/4)))

>eq2parabola(eq).equation()

-x**2 + y + 1

Diamo un occhio alle ellissi

>E=s.Ellipse(s.Point(0, 0), 5, 1)
>E.equation()

x**2/25 + y**2 - 1

>E.foci

(Point2D(-2*sqrt(6), 0), Point2D(2*sqrt(6), 0))

>E.focus_distance

2*sqrt(6)

>E.eccentricity

2*sqrt(6)/5

>E.is_tangent(r)

False

>E.intersection(r)

[Point2D(-5*sqrt(3)/2, 1/2), Point2D(5*sqrt(3)/2, 1/2)]

L'ellisse è definita a partire dal centro e i due semiassi

Un buon esercizio da assegnare o da mostrare in classe è trovare le tangenti ad una parabola passanti per un punto. Vediamo insieme come fare:

Prima di tutto occorre scrivere la retta generica per quel punto.

Occorre poi sostituire quest'espressione nell'equazione, porre

e risolvere per m. Vediamo come fare in Python...

y=y_0 + m(x-x_0)

\Delta = 0

def tangenti(CC,P):
    # CC è una conica, P un punto
    # in output le rette tangenti a CC passanti per P
    x,y=s.symbols('x y')
    m=s.symbols('m')
    eq=CC.equation(x,y)
    eq2=eq.subs(y, m*(x-P[0])+P[1]).as_poly(x).as_expr(x)
    a,b,c=eq2.coeff(x**2), eq2.coeff(x), eq2.subs(x,0)
    M=s.solve(b**2-a*c,m)
    return [retta(m,-m*P[0]+P[1]) for m in M]

5. Sistemi di equazioni lineari

I sistemi lineari possono essere risolti in python con il pacchetto numpy

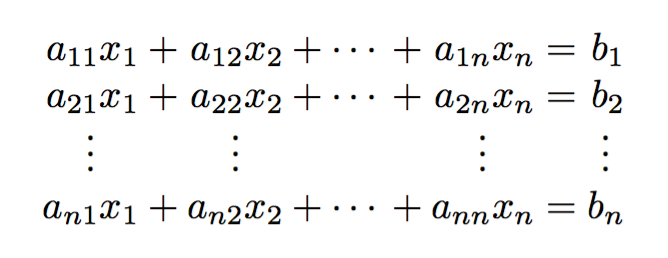
Vediamo un esempio:

>import numpy as np
>A=np.array([[1,2,3,4.5],[0,2,0,-1],[0,0,1,0],[1.5,0,0,1.4]])
>print(A)

[[ 1.   2.   3.   4.5]
 [ 0.   2.   0.  -1. ]
 [ 0.   0.   1.   0. ]
 [ 1.5  0.   0.   1.4]]

>b=np.array([1,0,4,1])
>print(b)

[1 0 4 1]

>x=np.linalg.solve(A,b)
>print(x)

[ 3.05109489 -1.27737226  4.         -2.55474453]

...e riscriviamo altre funzioni usando i metodi a noi noti!

Cramer:

>def cramer(A,b):
    dtA=np.linalg.det(A)
    x=np.zeros(b.shape)
    for i in range(len(x)):
        Ai=A.copy()
        Ai[:,i]=b.reshape(-1)
        x[i]=float(np.linalg.det(Ai))/float(dtA)
    return x
>
>cramer(A,b)
array([ 3.05109489, -1.27737226,  4.        , -2.55474453])

contro Gauss

>def MEG(A,b):
    A=np.array(A,dtype="float")
    b=np.array(b,dtype="float")
    x=np.zeros(b.shape)
    #triangolarizzazione
    n=len(b)
    for i in range(n-1):
        for j in range(i+1,n):
            m=A[j,i]/A[i,i]
            A[j,i:]-=m*A[i,i:]
            b[j]-=m*b[i]
    #sostituzioni
    x[-1]=b[-1]/A[-1,-1]
    for k in range(0,n-1)[::-1]:
        x[k]=(b[k]-np.dot(A[k,k+1:],x[k+1:]))/A[k,k]
    return x
>
>MEG(A,b)

array([ 3.05109489, -1.27737226,  4.        , -2.55474453])

Grazie per l'attenzione!