Public Discussion of the Research ativity

January, 15 2021

Academic Path:

  • [2012] MD in Mathematics, thesis on CT/SPECT image reconstruction from projection data.
  • [2017] PhD in Medical, Clinical and Experimental Sciences (Neurosciences curriculum). Research on PET/MRI neuroimaging and data analysis in MS, AD, Brain Tumour, PD.
  • [2018-2021] Three-years PostDoc at the PNC - Padova Neuroscience Center. Research on interpolation of discontinuous data with application to medical imaging, with focus on PET/MRI in neurodegenerative diseases.

Collaborations:

  • CAA: Padova-Verona research group on
    "Constructive Approximation and Applications".

  • CeSMuV (Centro Sclerosi Multipla del Veneto).
  • Nuclear Medicine Unit, Hospital of Padova.

  • Dorian Technologies - Diagnosis ORIented ANalysis (spin-off INFN, Genova).

Memberships:

Rete ITaliana di

Approssiamzione (GNCS)

Voting member of the PSF - Python Software Foundation

Scores and metrics

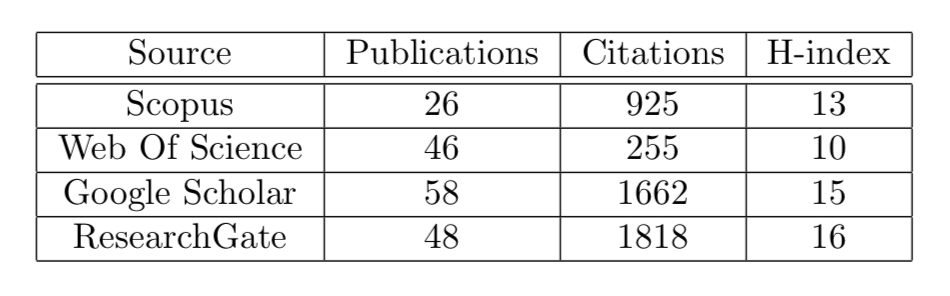
(Updated 13/Jan/2024)

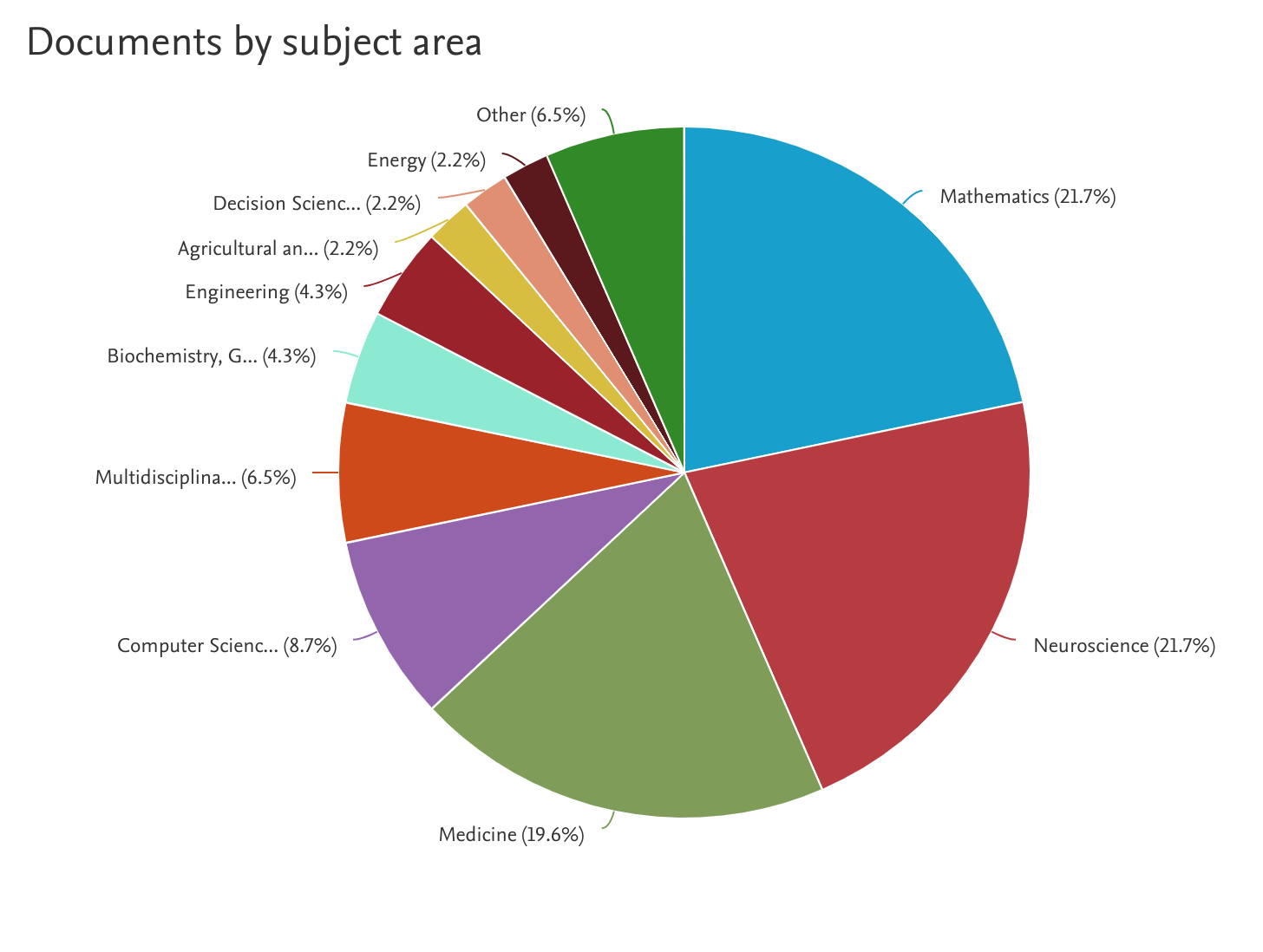
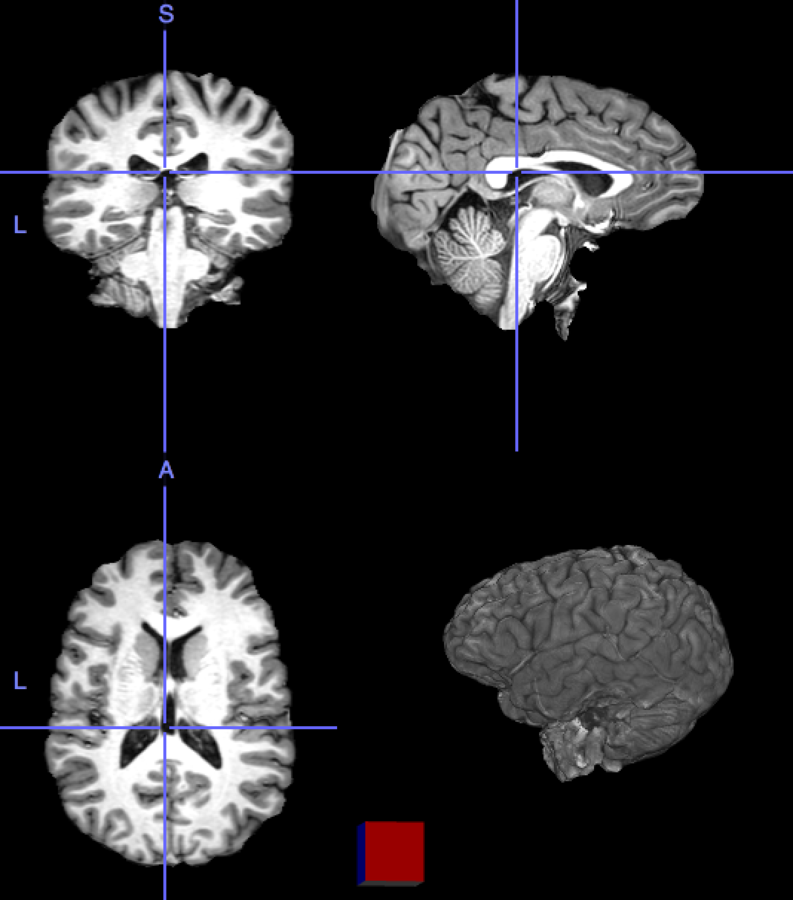
1. Neuroimaging

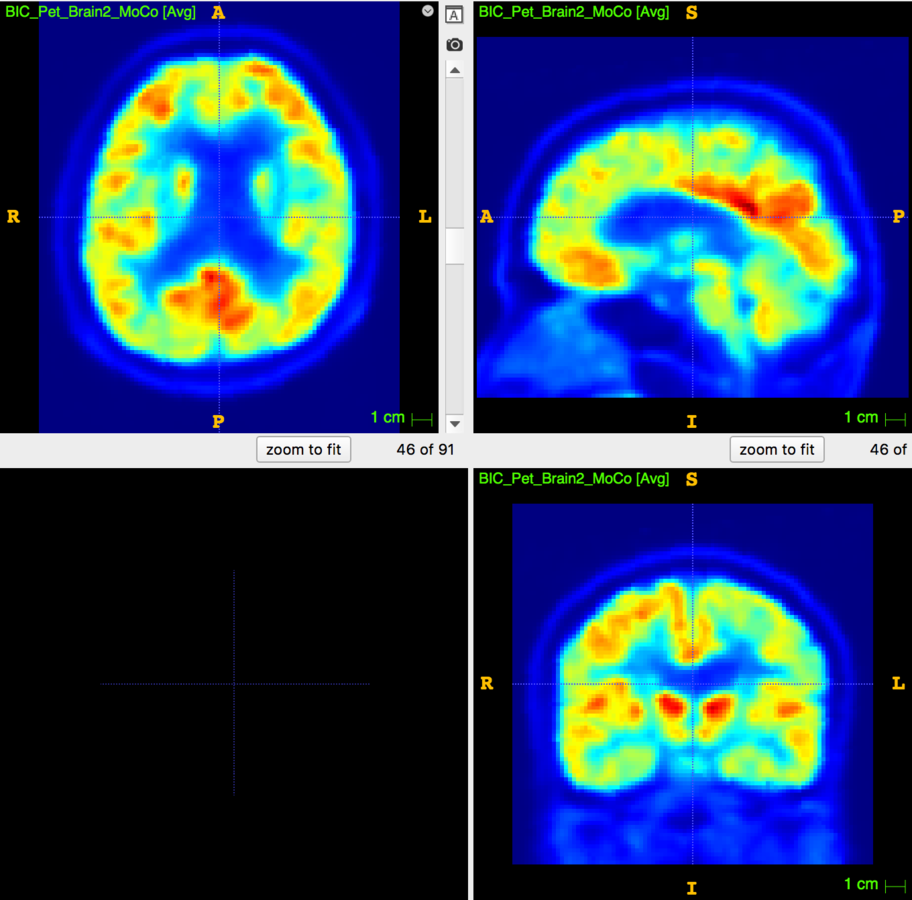
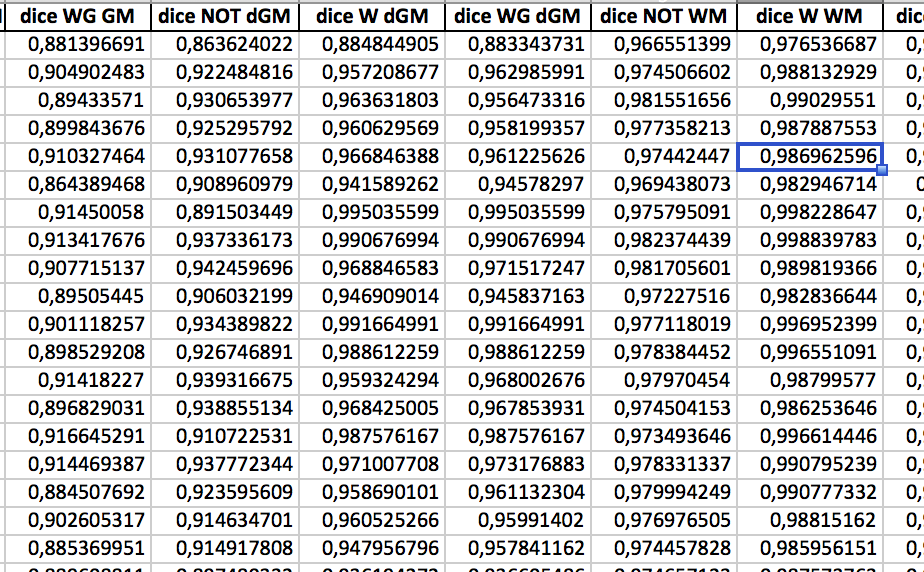
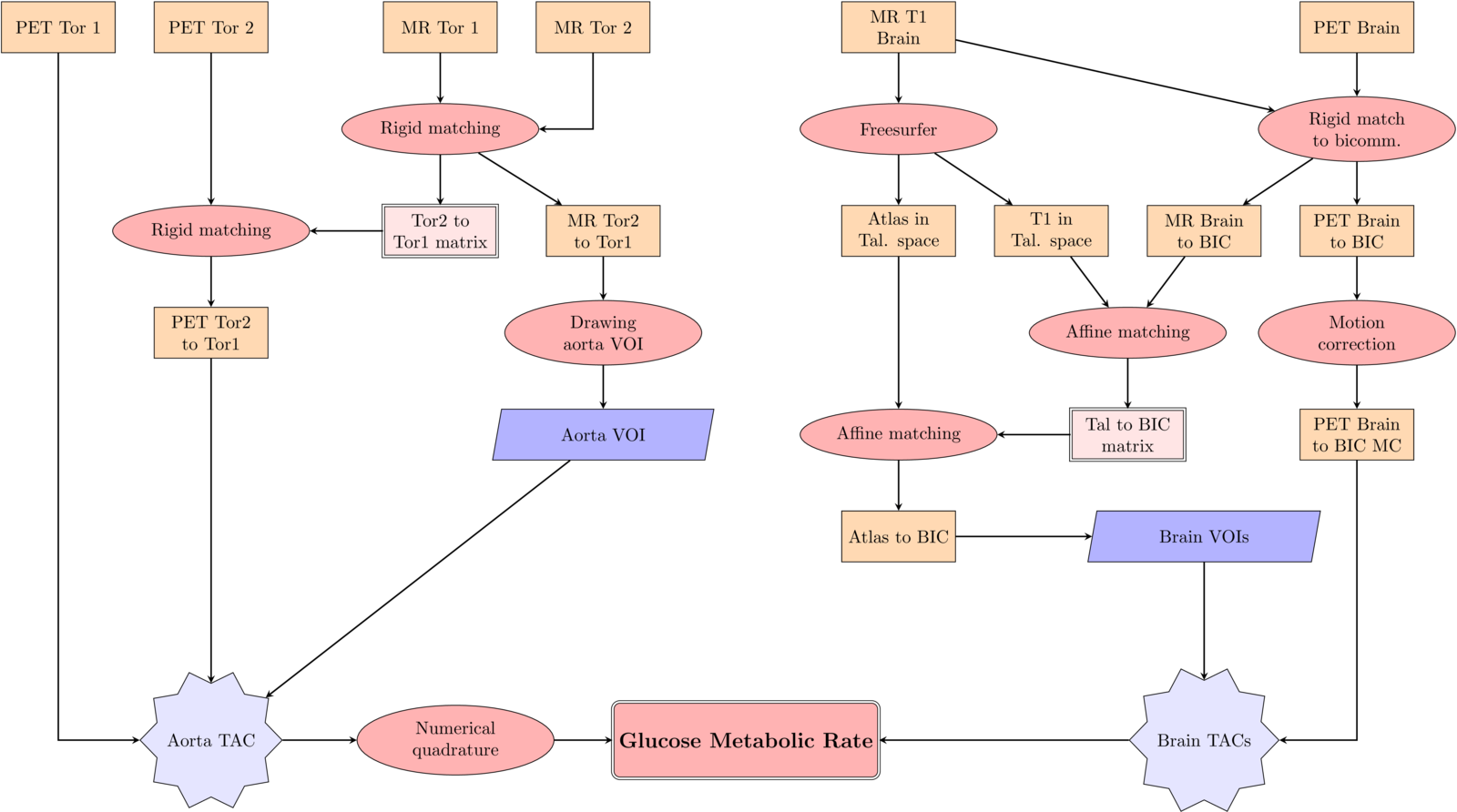
  • Acknowledge the system's limits.

from

D. Cecchin, D. Poggiali, L. Riccardi, P. Turco, F. Bui, S. De Marchi, Analytical and experimental FWHM of a gamma camera: theoretical and practical issues, PeerJ, doi:10.7717/peerj.722.

What does a numerical analyst do in clinical studies?

  • Awareness of neuroimaging algorithms and their applicability in different context.
  • Pipelining and automation.

from

M. Margoni, D. Poggiali, S. Zywicki, M. Rubin, A. Lazzarotto, S. Franciotta, M. G. Anglani, F. Causin, F. Rinaldi, P. Perini, M. Filippi, P. Gallo, Early red nucleus atrophy in relapse‐onset multiple sclerosis, HBM doi:10.1002/hbm.25213

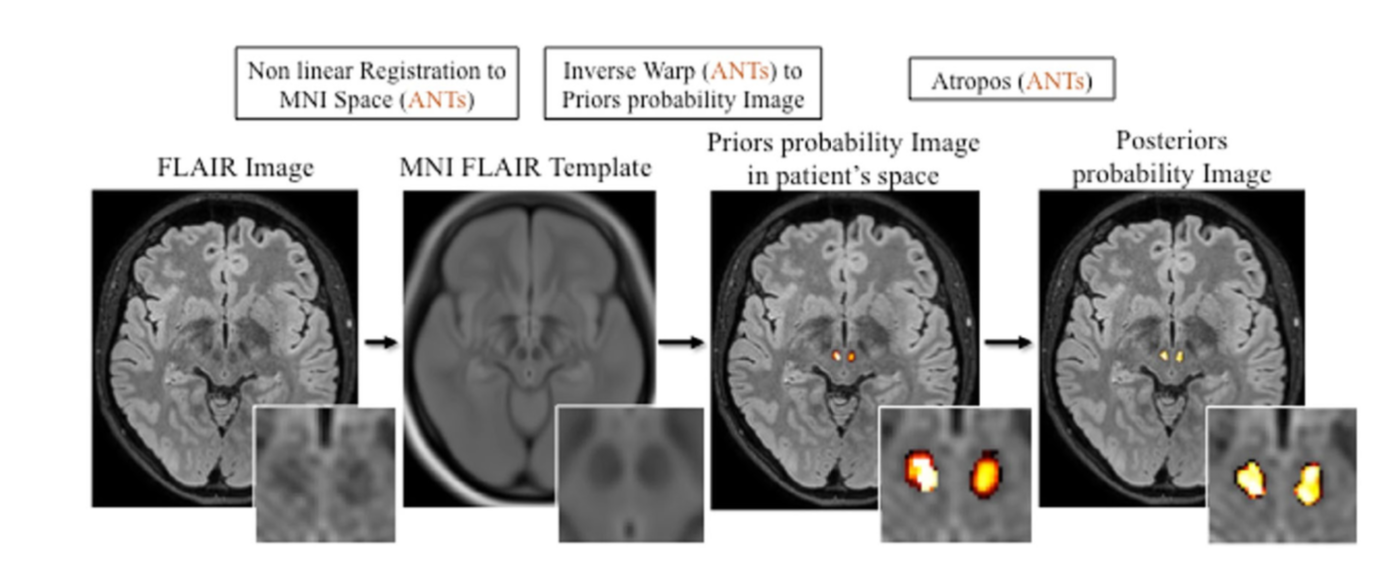
  • Preliminary statistic for feasibility of a study.
  • Dataviz.

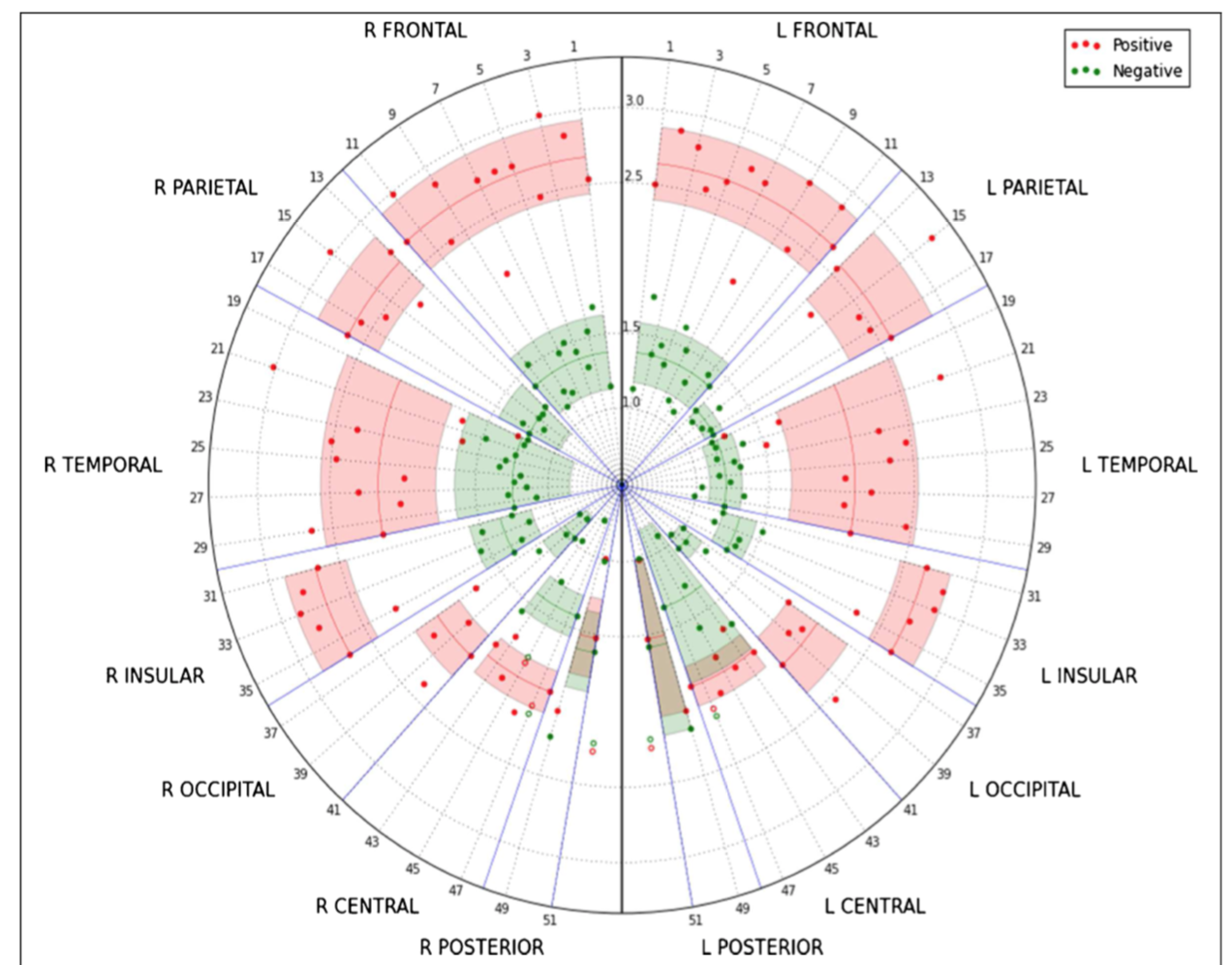
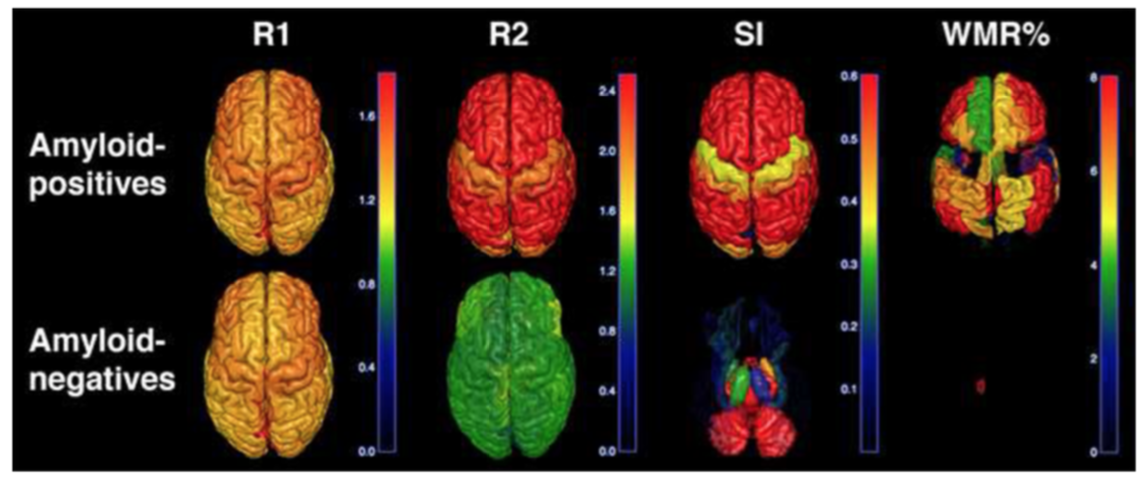
from

  • D. Cecchin, H. Barthel, D. Poggiali, A. Cagnin, S. Tiepolt, P. Zucchetta, P. Turco, P. Gallo, A.C. Frigo, O. Sabri, F. Bui, A new integrated dual time-point amyloid PET/MRI data analysis method, EJNMMI, doi:10.1007/s00259-017-3750-0.

  • Mathematical modelling.
  • Statistical analysis/Machine Learning.

from the Supplementary Materials of

  • D. Cecchin, H. Barthel, D. Poggiali, A. Cagnin, S. Tiepolt, P. Zucchetta, P. Turco, P. Gallo, A.C. Frigo, O. Sabri, F. Bui, A new integrated dual time-point amyloid PET/MRI data analysis method, EJNMMI, doi:10.1007/s00259-017-3750-0.

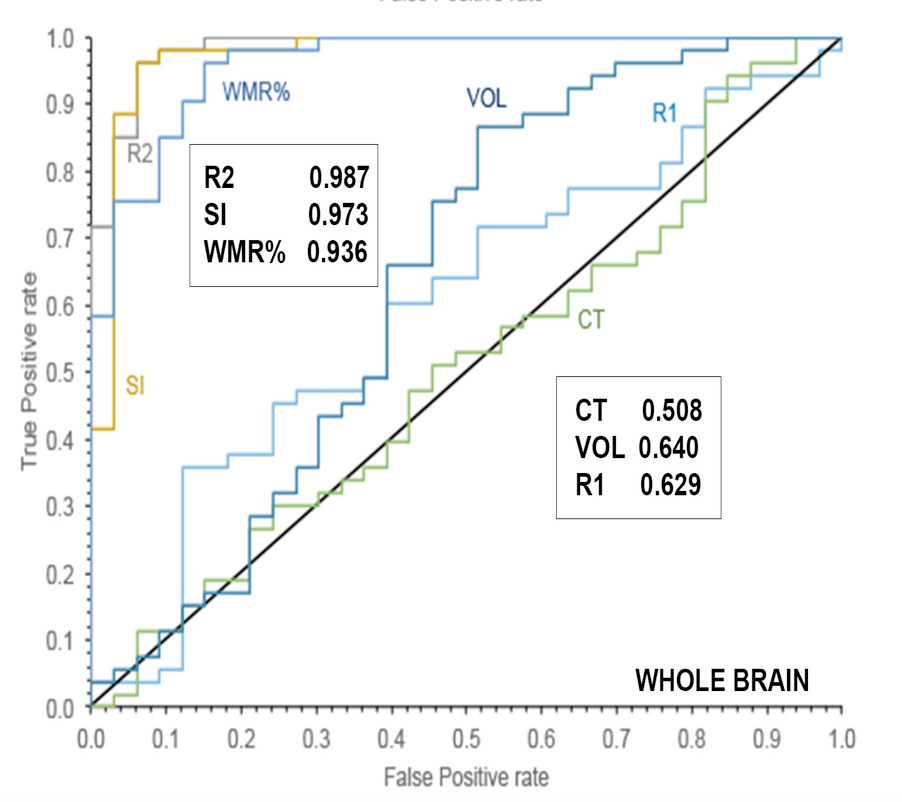
2.Numerical approximation and applications

Main topics of research:

  • Fake nodes interpolation.
  • Quadrature on Fake nodes.
  • Applications on imaging.

What is Fake Nodes interpolation?

Instead of interpolating on the nodes x you define a mapping function S and interpolate over the fake nodes S(x).

f = lambda x: np.log(x**2+1)
x = np.linspace(-1,1,10)
y = f(x)
xx = np.linspace(-1,1,100)



yy = my_fancy_interpolator(x,y,xx)
f = lambda x: np.log(x**2+1)
x = np.linspace(-1,1,10)
y = f(x)
xx = np.linspace(-1,1,100)

S = lambda x: -np.cos(np.pi * .5 * (x+1))

yy = my_fancy_interpolator(S(x),y,S(xx))

Given a function

f: \Omega \subseteq \mathbb{R}^d \longrightarrow \mathbb{R}\;\;\;\;\; {d \in \mathbb{N}},

a set of distinct nodes

X = \{ x_0, \dots, x_N\} \subset \Omega,

and a set of basis functions

\mathcal{B} = \{ b_i: \Omega \longrightarrow \mathbb{R} \}_{i = 0, \ldots, N}

The interpolant is given by a function

\displaystyle \mathcal{P}(\bm{x}) = \sum_{i=0}^{N} c_i b_i(\bm{x})

s.t.

\mathcal{P}(\bm{x}_i)=y_i:=f(\bm{x}_i) \;\;\forall i
\mathcal{B} = \{ b_i \circ S: \Omega \longrightarrow \mathbb{R}^d \}_{i = 0, \ldots, N}
\displaystyle \mathcal{R}^s(\bm{x}) = \sum_{i=0}^{N} c_i b_i(S(\bm{x}))
\mathcal{R}^s(\bm{x}_i)=y_i:=f(\bm{x}_i) \;\;\forall i

This process can be seen equivalently as:

1. Interpolation over the mapped basis

\[\mathcal{B}^s = \{b_i \circ S \}_{i=0, \dots, N}.\]

2. Interpolation over the original basis \(\mathcal{B}\) of a function \(g: S(\Omega) \longrightarrow\mathbb{R}\)

at the fake nodes 

\[S(X) = \{S(x_i) \}_{i=0, \dots, N}.\]

 \(g\in C^s\) must satisfy \(g(S(x_i)) = f(x_i)\;\;\forall i\).

If \(\mathcal{P} \approx g \) on \(S(X)\) with the original basis,

then \(\mathcal{R}^s = \mathcal{P} \circ S \approx f \)  on \(X\).

This allow to treat Runge Effect...

from

  • S. De Marchi, F. Marchetti, E. Perracchione, D. Poggiali, Polynomial interpolation via mapped bases without resampling, JCAM, doi:10.1016/j.cam.2019.112347.

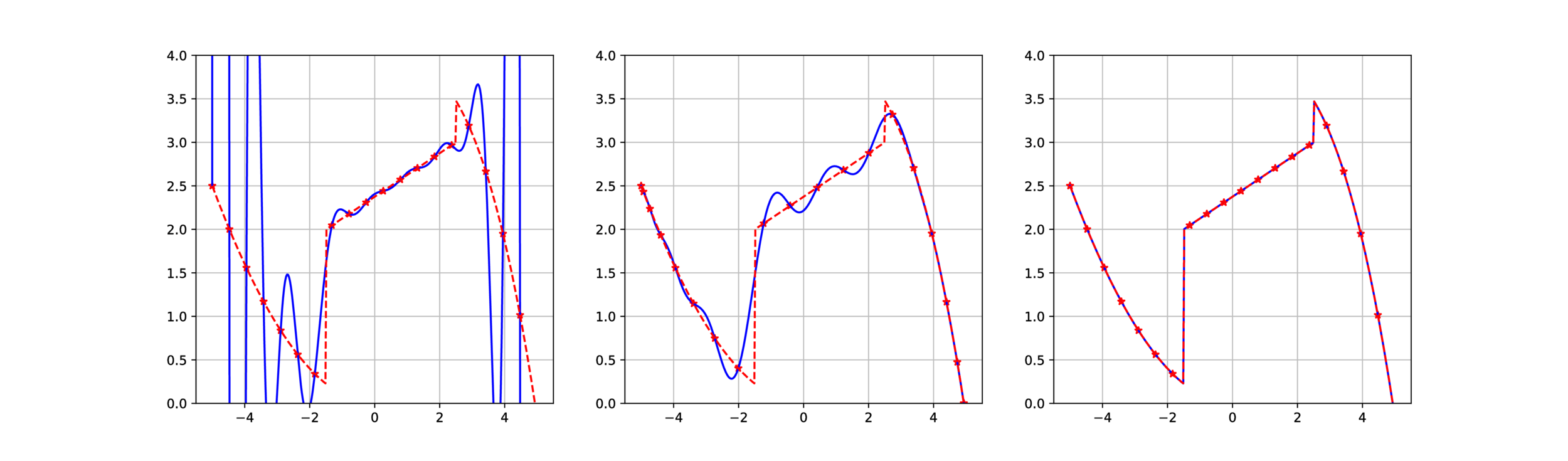
...and Gibbs Effect, exploiting prior knowledge on discontinuity

from

  • S. De Marchi, F. Marchetti, E. Perracchione, D. Poggiali, Polynomial interpolation via mapped bases without resampling, JCAM, doi:10.1016/j.cam.2019.112347.

from

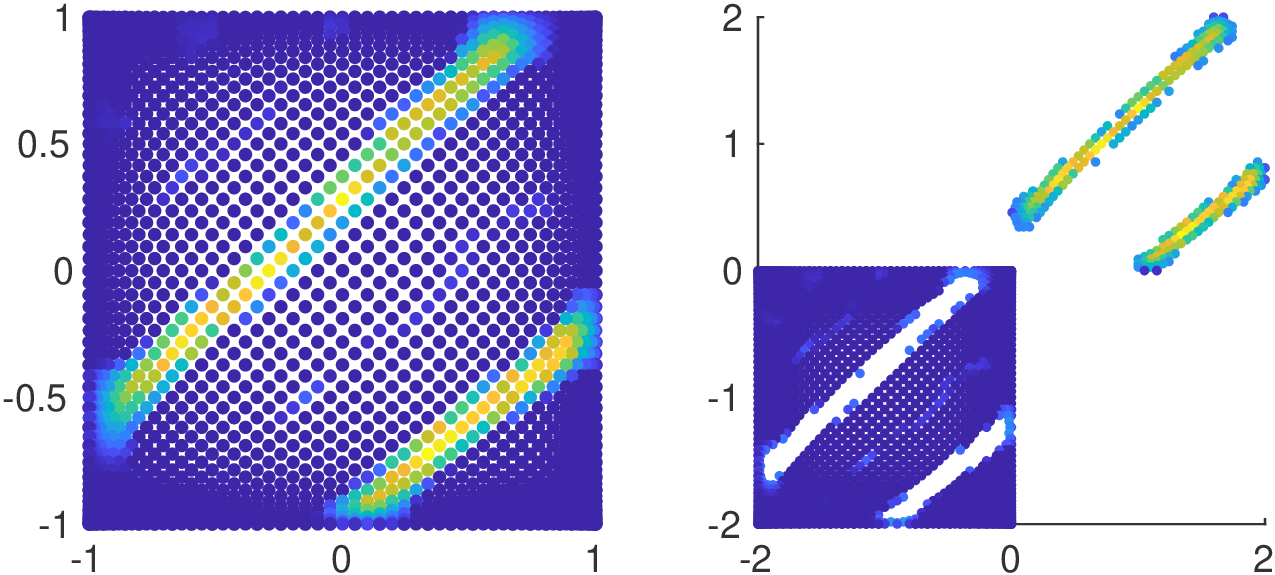
Fake Nodes applies to arbitrary-dimensioned data.

Numerical quadrature can also benefit from Fake Nodes Approach

\int_a^b f(x) dx \approx \sum_{i=0}^n f_i \int_a^b l_i(x) dx
\int_a^b f(x) dx \approx \sum_{i=0}^n f_i \int_{a^*}^{b^*} l_i(S(x)) dx

from

  • S. De Marchi, G. Elefante, E. Perracchione, D. Poggiali, Quadrature at Fake Nodes, DRNA.

  • G. Cappellazzo, W. Erb, F. Marchetti, D. Poggiali, On Kosloff Tal-Ezer least-squares quadrature formulas, BIT Numerical Mathematics, doi:10.1007/s10543-023-00948-0

Applications to medical imaging:

MPI reconstruction.

from

  • S. De Marchi, W. Erb, E. Francomano, F. Marchetti, E. Perracchione, D. Poggiali, Fake Nodes approximation for Magnetic Particle Imaging, Conference paper, MELECON 2020 doi:10.1109/MELECON48756.2020.914058

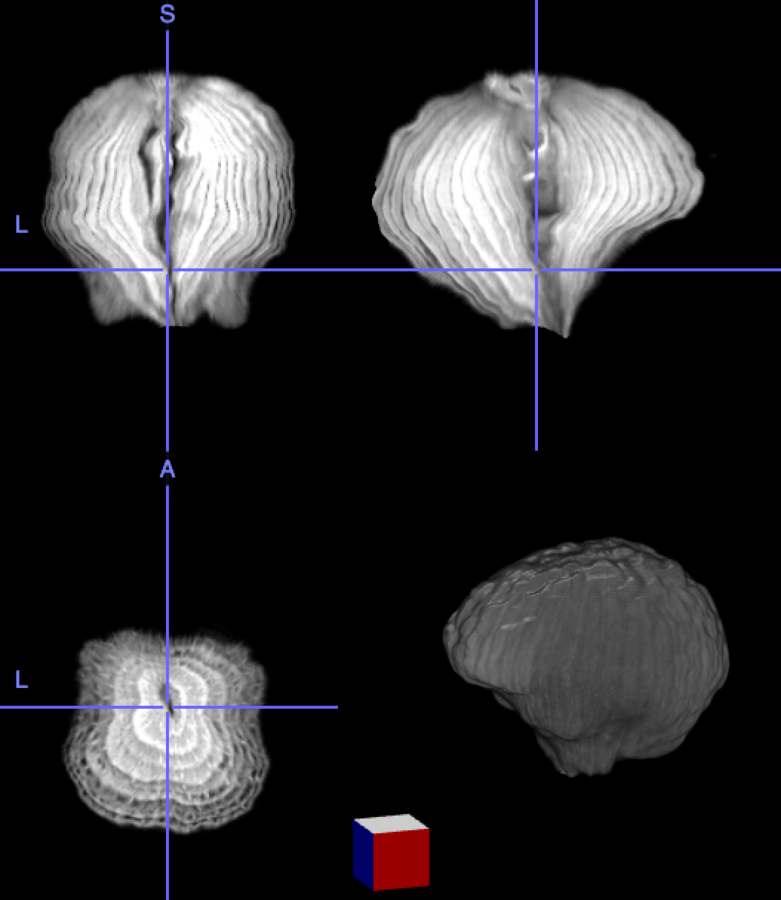
Applications to medical imaging:

3D multimodal image resampling.

from

  • D. Poggiali, D. Cecchin, C. Campi, S. De Marchi, Oversampling errors in multimodal medical imaging are due to the Gibbs effect, Mathematics, doi:10.3390/math9121348

  • D. Poggiali, D. Cecchin, S. De Marchi, Reducing the Gibbs effect in multimodal medical imaging by the Fake Nodes Approach, JCMDS, doi:10.1016/j.jcmds.2022.100040

High resolution "morphological" image

1mm^3

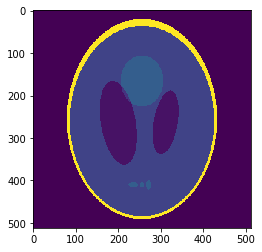
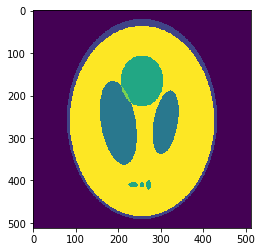
Segmentation mask

1mm^3

Low resolution "functional" image

8mm^3

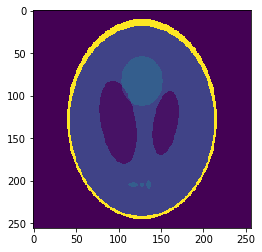
Applications to medical imaging:

3D multimodal image resampling.

from

  • D. Poggiali, D. Cecchin, C. Campi, S. De Marchi, Oversampling errors in multimodal medical imaging are due to the Gibbs effect, Mathematics, doi:10.3390/math9121348

  • D. Poggiali, D. Cecchin, S. De Marchi, Reducing the Gibbs effect in multimodal medical imaging by the Fake Nodes Approach, JCMDS, doi:10.1016/j.jcmds.2022.100040

Def Let \(f: \Omega \subseteq \mathbb{R}^d \longrightarrow \mathbb{R}\) be a piecewise continuous function. The function \(f\) admits a (local) modulus of continuity 

$$\omega_{\bm x_0}(\delta): \mathbb{R}^{+} \longrightarrow \mathbb{R}^{+}$$
in \(\bm x_0\in\Omega\) if
\[ |f(\bm x) - f(\bm x_0) | \leq \omega_{\bm x_0}(\delta) \;\;\forall \bm x \in \Omega \text{ s.t. } \|\bm x- \bm x_0\|\leq \delta, \]
where \(\|\cdot\|\) is an arbitrary norm.

Def Image interpolation by convolution in applications is defined as

\[\mathcal{P}_f (\bm{x}) = \sum_{ijk} f(\bm{x}_{ijk})W_{ijk}(\bm{x})\]

with

\[W_{ijk}(x, y, z) = w(x-x_i)\; w(y-y_i) \;w(z-z_i)\]

the separable basis with \(w(t-t_i)\) a cardinal, normalized and compact-supported basis over an equispaced grid.

Applications to medical imaging:

3D multimodal image resampling.

from

  • D. Poggiali, D. Cecchin, C. Campi, S. De Marchi, Oversampling errors in multimodal medical imaging are due to the Gibbs effect, Mathematics, doi:10.3390/math9121348

  • D. Poggiali, D. Cecchin, S. De Marchi, Reducing the Gibbs effect in multimodal medical imaging by the Fake Nodes Approach, JCMDS, doi:10.1016/j.jcmds.2022.100040

Theorem Let \(f\) be a d-variate and bounded function admitting a local modulus of continuity \(\omega_{\bm x} (\delta)\). Let \(\mathcal{P}f\) be its interpolant by convolution. Then, there exits some \(\delta^* > 0\) such that
\[ |\mathcal{P}f (\bm x) - f(\bm x)| \leq \omega_{\bm x} (\delta^*)\,. \]

Lemma 4.1 A d-variate, Lipschitz-continuous function \(f\) admits a modulus of continuity of the form
\[\omega(\delta) = K\delta \]
being \(K\) the Lipschitz constant.

Lemma 4.2 A piecewise d-variate, Lipschitz-continuous function \(f\) admits a modulus of continuity of the form
\[\omega(\delta) = K\delta + D \]

Applications to medical imaging:

3D multimodal image resampling.

from

  • D. Poggiali, D. Cecchin, C. Campi, S. De Marchi, Oversampling errors in multimodal medical imaging are due to the Gibbs effect, Mathematics, doi:10.3390/math9121348

  • D. Poggiali, D. Cecchin, S. De Marchi, Reducing the Gibbs effect in multimodal medical imaging by the Fake Nodes Approach, JCMDS, doi:10.1016/j.jcmds.2022.100040

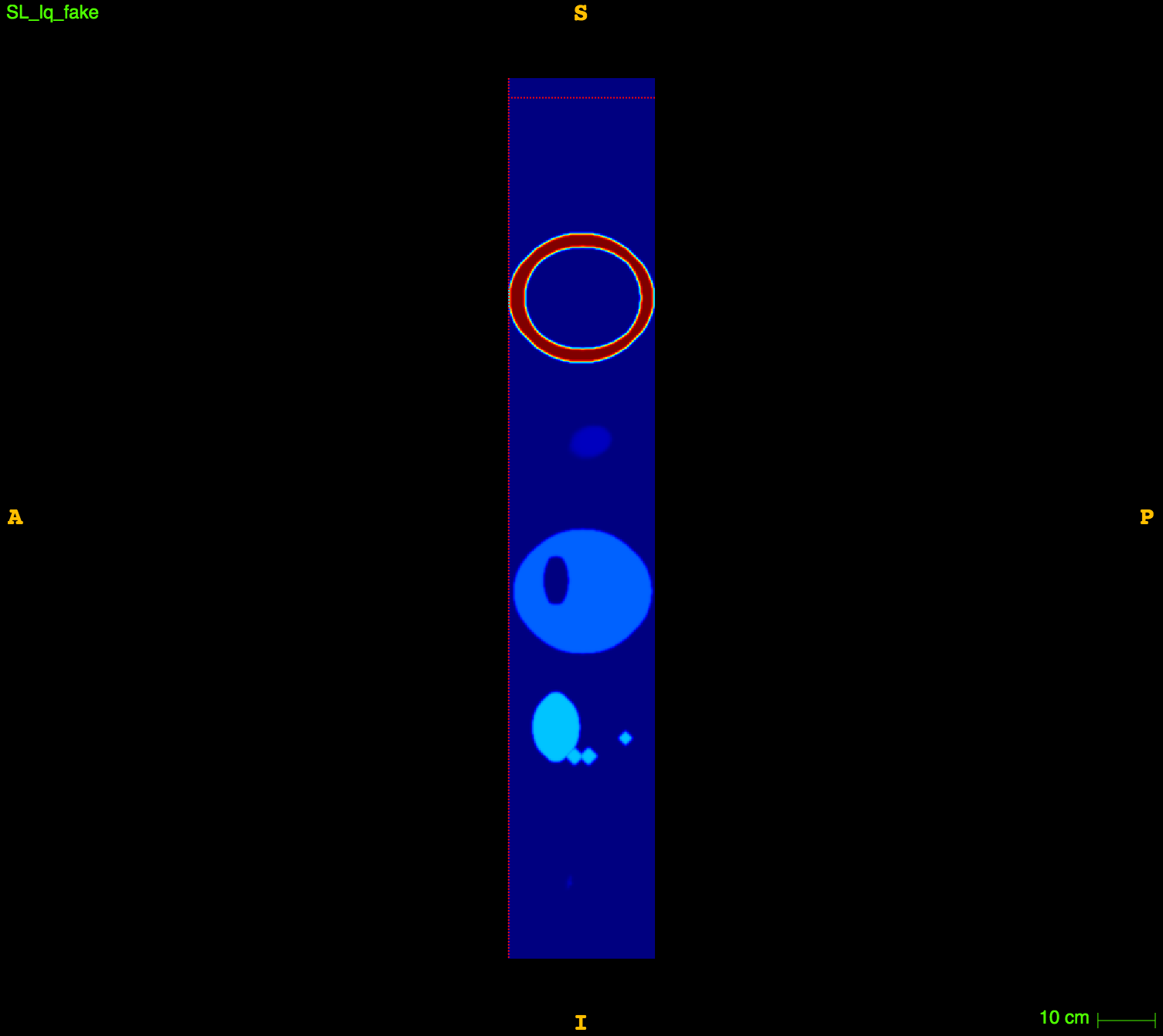
\((2mm)^3\)

\(1mm^3\)

Fake image

Applications to medical imaging:

3D multimodal image resampling.

from

  • D. Poggiali, D. Cecchin, C. Campi, S. De Marchi, Oversampling errors in multimodal medical imaging are due to the Gibbs effect, Mathematics, doi:10.3390/math9121348

  • D. Poggiali, D. Cecchin, S. De Marchi, Reducing the Gibbs effect in multimodal medical imaging by the Fake Nodes Approach, JCMDS, doi:10.1016/j.jcmds.2022.100040

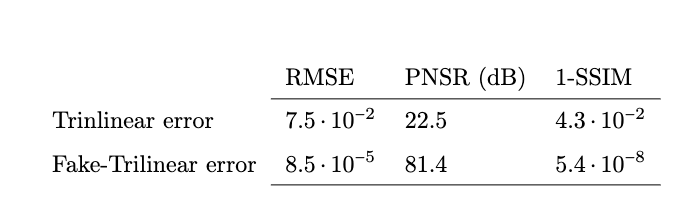
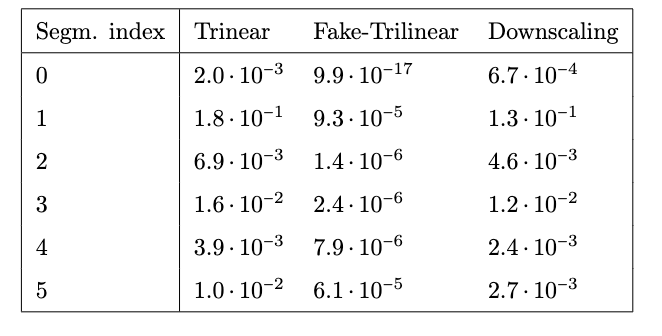
3. Open source, open science

I like to write (mostly in Python), share as Open Source, and maintain my own code whenever it is possible. This makes my work:

  • Accessible to anyone;
  • Verifiable by anyone;
  • Reproducible;
  • More visible (and hopefully cited).

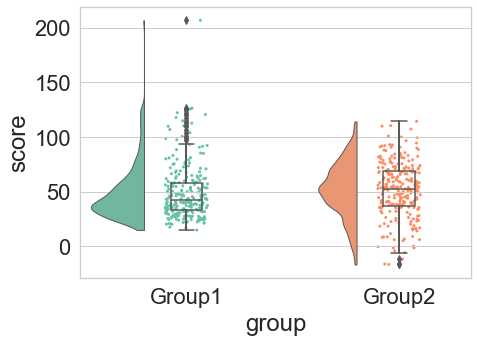
The RainCloud is an open source project. I wrote and maintain the python version.

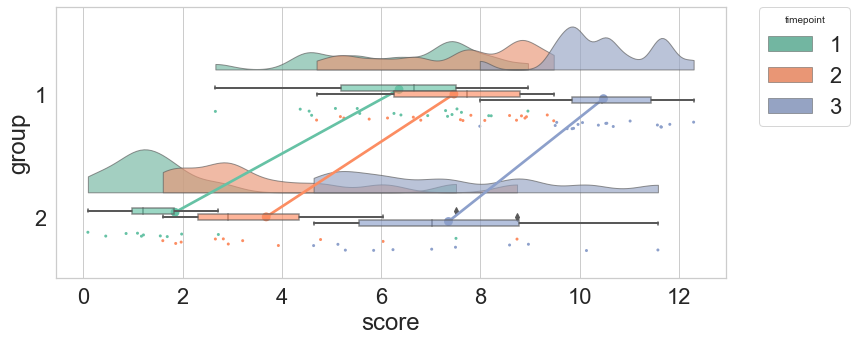
from

  • M. Allen, D. Poggiali, K. Whitaker, T. R. Marshall, J. van Langen, R.A. Kievit, Raincloud plots: a multi-platform tool for robust data visualization, WOR, doi:10.12688/wellcomeopenres.15191.2.

Open science is more than just open source/open data.

from

  • R. Gau, S. Noble, K. Heuer et al., Brainhack: developing a culture of open, inclusive, community-driven neuroscience, Neuron, doi:10.1016/j.neuron.2021.04.001

Teaching experience

[2023] Lab Professor of "Introduction to Numerical Calculus" for Astronomy; Main Teacher: Prof M. Vianello, 2CFU.

[2022] Lab Professor of "Introduction to Numerical Calculus" for Astronomy; Main Teacher: Prof M. Vianello, 2CFU.

[2021] Professor of "Introduction to Numerical Calculus" for Astronomy, 6CFU.

[2020] Lab Professor of "Numerical Calculus" for Mechanical Engineering (tracks 1 and 2); Main Teacher: Prof S. De Marchi, 6CFU.

[2019] Lab Professor of "Numerical Calculus" for Energy Engineering; Main Teacher: Prof A. Sommariva, 1CFU.

[2018] Professor of "Introduction to Python" for the Data Science Summer School, University of Trento, 6 CFU.

 

[2012-19] Teaching Assistant (TA) in Numerical Calculus for 8 courses.

[2017-2019] High school Math/Physics substitute teacher. Total time: 18 months.

Editorial Aticivity

Reviewer: Peer review for the following journals (alphabetical order):

  • Dolomites Research Notes on Approximation;
  • Electronic Transactions on Numerical Analysis;
  • Frontiers in Neuroscience;
  • Journal of Applied Analysis;
  • Journal of Applied Mathematics and Computing;
  • Mathematical Biosciences and Engineering;
  • Mathematics and Computers in Simulation;
  • Scientific Reports;
  • Transactions on Image Processing.

 

Editor: Section Topical Advisory Panel Member for section Mathematical Biology of Mathematics.

Thanks for listening!

Made with Slides.com