The Geometry of Domino Tilings

David Radcliffe

dradcliffe@gmail.com

Introduction

 

A domino is a 2x1 rectangular region in the plane.

 

Given a polygonal region P in the plane, we are interested in the following questions.

  1. Does P admit a tiling by dominoes?
  2. Is there an efficient algorithm to find a domino tiling of P, if one exists?
  3. In how many ways can P be tiled by dominoes?
  4. What is the "geometry" of the set of all domino tilings of P?

 

  • Bullet One
  • Bullet Two
  • Bullet Three

Orienting the edges

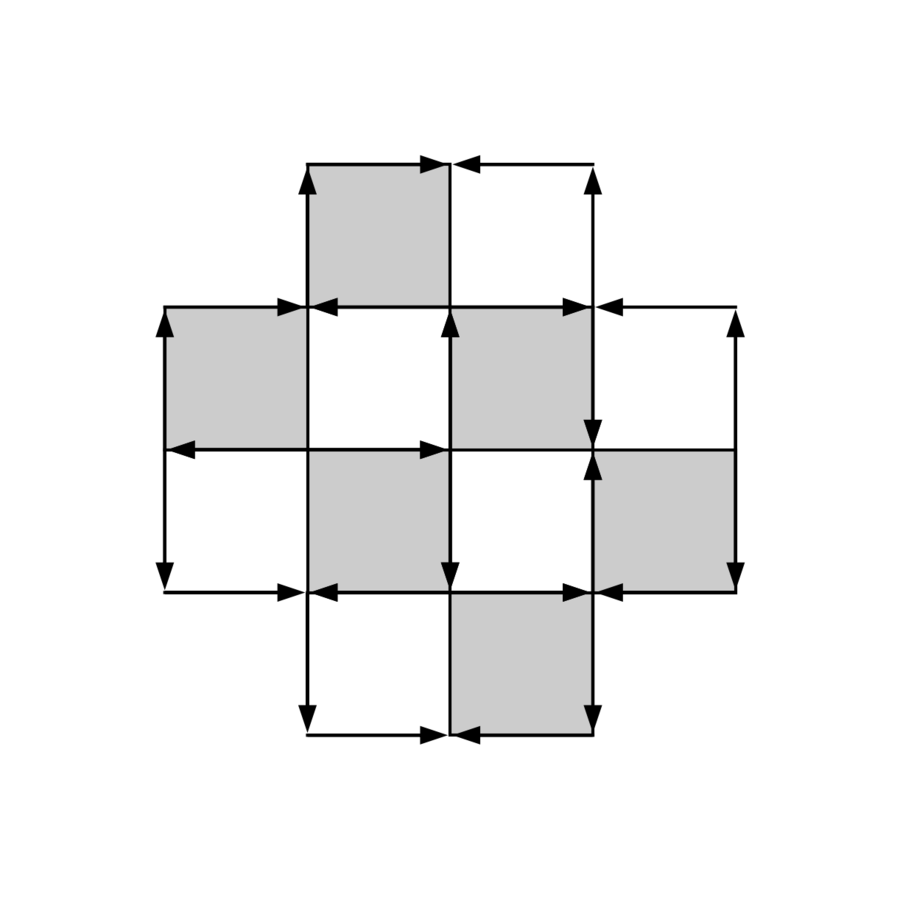
Boundary of a polygonal region

If a polygonal region is tiled by dominoes, then the "integral" around the boundary is zero.

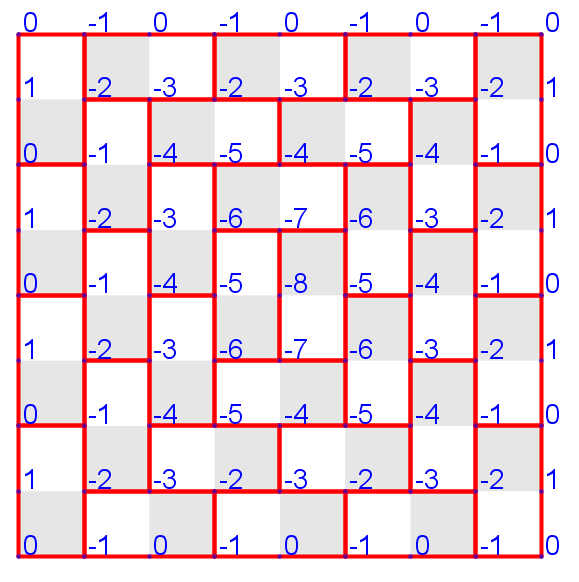
The height function

A domino tiling determines a unique height function on the grid points, up to a constant.

Conversely, a valid height function determines a unique domino tiling.

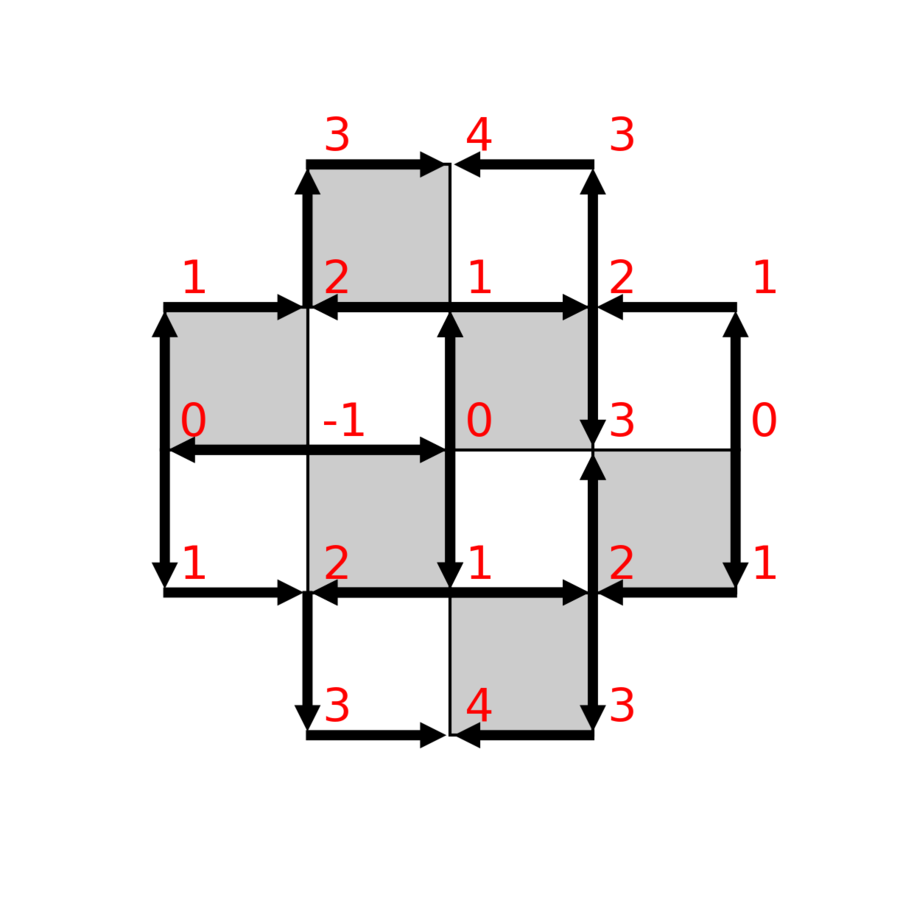
Properties of height functions

  1. The base point has height 0.
  2. For each directed edge uv on the boundary,
     
  3. For each directed edge uv in the interior,
h(v) - h(u) = 1.
h(v)−h(u)=1.h(v) - h(u) = 1.
h(v) - h(u) \in \{-3, 1\}.
h(v)−h(u)∈{−3,1}.h(v) - h(u) \in \{-3, 1\}.

There is a one-to-one correspondence between domino tilings and height functions.

Order properties of height functions

  1. The set of height functions on a polygonal region P forms a partially ordered set.

     
  2. The maximum or minimum of two height functions is also a height function.


     
  3. Therefore, the set of height functions on a polygonal region is a distributive lattice.
h_1 \leq h_ 2 \Longleftrightarrow \forall v:h_1(v) \le h_2(v)
h1≤h2⟺∀v:h1(v)≤h2(v)h_1 \leq h_ 2 \Longleftrightarrow \forall v:h_1(v) \le h_2(v)
(h_1 \vee h_2)(v)=\max\{h_1(v), h_2(v)\}
(h1∨h2)(v)=max{h1(v),h2(v)}(h_1 \vee h_2)(v)=\max\{h_1(v), h_2(v)\}
(h_1 \wedge h_2)(v) = \min\{h_1(v), h_2(v)\}
(h1∧h2)(v)=min{h1(v),h2(v)}(h_1 \wedge h_2)(v) = \min\{h_1(v), h_2(v)\}

Local flips

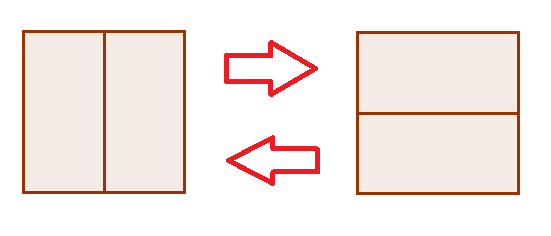
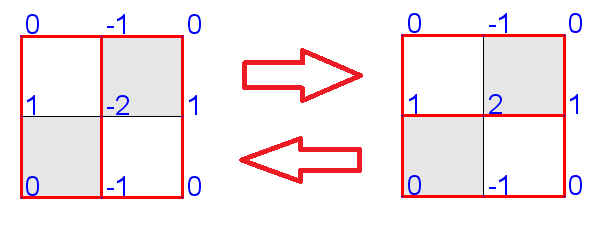
  • A local flip is a 90 degree rotation of a 2x2 square formed by two adjacent dominoes.
  • A local flip increases or decreases the height of the center of the square by 4, but does not change the heights of the other grid points.

Local maxima and minima

  • A local maximum (or minimum) is an interior grid point that is higher (or lower) than its neighbors.
  • Local extrema occur at the center points of 2x2 blocks
  • A local flip converts a local maximum to a local minimum, and vice versa.

Distance function

The distance between two height functions is
 

 

 

Theorem 1. Any two domino tilings can be connected by a sequence of local flips.

 

Theorem 2. The minimum number of flips required to transform one tiling to another is equal to the distance between the height functions.

d(h_1, h_2) = \dfrac14 \sum\limits_v |h_1(v) - h_2(v)|.
d(h1,h2)=14∑v∣h1(v)−h2(v)∣.d(h_1, h_2) = \dfrac14 \sum\limits_v |h_1(v) - h_2(v)|.

Highest domino tiling

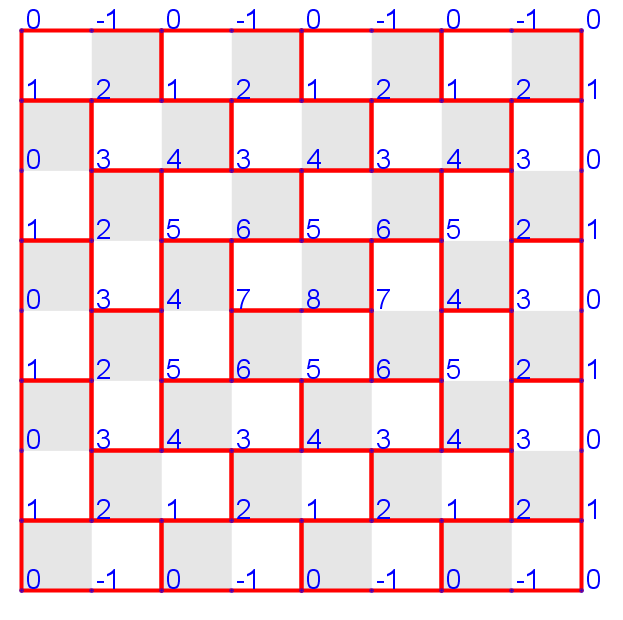
\dfrac14 \sum\limits_v h(v) = \dfrac12 \cdot (7^2 + 5^2 + 3^2 + 1^2) = 42
14∑vh(v)=12⋅(72+52+32+12)=42\dfrac14 \sum\limits_v h(v) = \dfrac12 \cdot (7^2 + 5^2 + 3^2 + 1^2) = 42

Lowest domino tiling

\dfrac14 \sum\limits_v h(v) = -\dfrac12 \cdot (7^2 + 5^2 + 3^2 + 1^2) = -42
14∑vh(v)=−12⋅(72+52+32+12)=−42\dfrac14 \sum\limits_v h(v) = -\dfrac12 \cdot (7^2 + 5^2 + 3^2 + 1^2) = -42

Visualizing the set of all domino tilings

Made with Slides.com