監督式機器學習

Supervised Learning

Denny Chen
denny20700@gmail.com
2020.03.30

監督?非監督?

● 監督式學習（Supervised Learning）: 在訓練的過程中告訴機器答案、也就是「有標籤」的資料，比如給機器各看了 1000 張蘋果和橘子的照片後、詢問機器新的一張照片中是蘋果還是橘子。

● 非監督式學習（Unsupervised Learning）: 訓練資料沒有標準答案、不需要事先以人力輸入標籤，故機器在學習時並不知道其分類結果是否正確。訓練時僅須對機器提供輸入範例，它會自動從這些範例中找出潛在的規則。
還有半監督學習，有興趣可以自己google

分類器 Classification

決策樹 Decision Tree
隨機森林 Random Forest 
Boosting淺談
Model
Function
rpart
randomForest
羅吉斯回歸 Logistic Regression
glm
caret
套件
新套件
補充
工具
支撐向量機 Support Vector Machine
svm

1. 𝑃(𝐶𝑗) 是類別𝐶𝑗出現的機率，稱為先驗機率 (priori probability)；
2. 𝑃(𝑥|𝐶𝑗) 是條件密度函數，即給定類別 𝐶𝑗，數據點 𝑥 的機率密度函數，也稱為似然 (likelihood)；
3. 𝑃(𝑥) 是數據點 𝑥 的機率密度函數，稱為證據 (evidence)，算式為                                               
4. P(Cj|x) 是指在給定數據點 𝑥 的情況下，該點屬於 𝑃(𝐶𝑗) 的機率，稱為後驗機率 (posterior probability)。

考慮二類別分類問題，即 𝑘=2。使用貝氏定理，數據點 𝑥 的對數賠率 (log odds) 可表示為         


假設條件密度 𝑃(𝑥|𝐶1) 和 𝑃(𝑥|𝐶2) 為常態分布並有相同的共變異數矩陣，對數賠率可簡化為 𝑥 的線性函數，稱為羅吉斯迴歸：

 

解開對數賠率之後可得出後驗機率

 

將𝑎=𝑤𝑇𝑥+𝜔0帶入得出

p(C_j|x)=\frac{p(x|C_j)p(C_j)}{p(x)}

羅吉斯回歸

羅吉斯回歸使用貝氏定理作為基礎:

log\frac{p(C_1|x)}{p(C_2|x)}=log\frac{p(x|C_1)p(C_1)}{p(x|C_2)p(C_2)}
p(x)=p(x|C_1)p(C_1)+...+p(x|C_k)p(C_k)
log\frac{p(C_1|x)}{p(C_2|x)}=log\frac{p(C_1|x)}{1-p(C_1|x)}=w^Tx+w_0

(對數賠率)

p(C_1|x)=\frac{1}{1+exp(-(w^Tx+w_0))}=f(w^Tx+w_0)
f(a)=\frac{1}{1+exp(-a)}
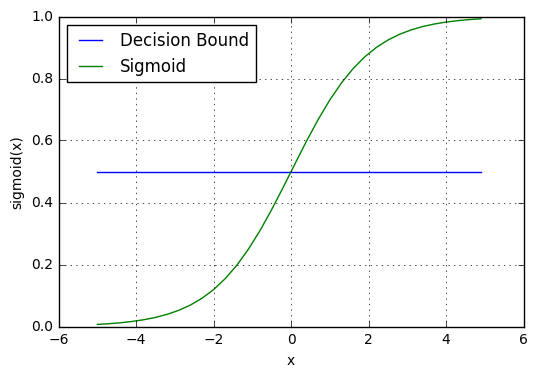
邏輯函數 logistic function

羅吉斯回歸

簡單來說:

羅吉斯回歸的對數函數採用sigmoid函數，利用最大概似估計法與柏努力分布的機率密度函數對參數β做估計，並用梯度下降法來逼近最佳解以求解。

梯度求解完

 

 

α為學習率。

那什麼是梯度下降? 學習率又是什麼?

這邊我要強調一點，glm 全稱 general linear model，中文是「廣義線性模型」，當y分布為二項式，連結函數為logit 才是羅吉斯回歸。

g(p)=ln(\frac{p}{1-p})
以此建模的廣義線性模型通常稱為logistic迴歸

梯度下降? 學習率?

click for link

羅吉斯回歸

羅吉斯回歸

Usage
glm(formula, family = gaussian, data, weights, subset, na.action, start = NULL, etastart, mustart, offset, control = list(…), model = TRUE, method = "glm.fit", x = FALSE, y = TRUE, singular.ok = TRUE, contrasts = NULL, …)

glm.fit(x, y, weights = rep(1, nobs), start = NULL, etastart = NULL, mustart = NULL, offset = rep(0, nobs), family = gaussian(), control = list(), intercept = TRUE, singular.ok = TRUE)

Argument 

family : a description of the error distribution and link function to be used in the model. For glm this can be a character string naming a family function, a family function or the result of a call to a family function. For glm.fit only the third option is supported. (See family for details of family functions.)
family

羅吉斯回歸

logistic_reg <- glm(formula = y ~ x, data = .data, family = "binomial")

我個人來說幾乎只使用這樣。

   1. 顯著性

對於我，羅吉斯的用處就是

   2. 共線性

   3. 係數方向

所以接下來會介紹樹模型

決策樹

         決策樹會針對不同的特徵欄位(column)進行分裂，每一次分裂都會將樣本區隔到不同的預測分群當中，透過決策樹不斷的向下生長，建立出一個分類的邊界，從而將下次輸入的資料進行預測。

         而決策樹的分裂有著兩種主要的評估依據，我們稱之為不純度，不純度依照分類正確的機率(p)計算，分別為熵(entropy)以及吉尼係數(Gini)，其公式為：

 

 

Entropy=-p log_2p-(1-p)log_2(1-P)
Gini=p^2+(1-p)^2

本日焦點

決策樹

Entropy=-p log_2p-(1-p)log_2(1-P)
TRUE

50%

FALSE

50%

資訊熵:白話來描述可為資訊雜亂程度的量化

資訊不純度 : 1

TRUE

95%

FALSE

5%

資訊不純度 : 0.2864

決策樹會將上一層節點的不純度與下一層進行相減，所得出的數值稱為資訊增益(Information Gain)，透過追求最多的資訊增益的過程，決策樹會自動找尋到最佳的分裂位置。

父節點

不純度 1

子節點

不純度 0.8

子節點

不純度 0.7

加權不純度 0.76

資訊增益 0.24

決策樹

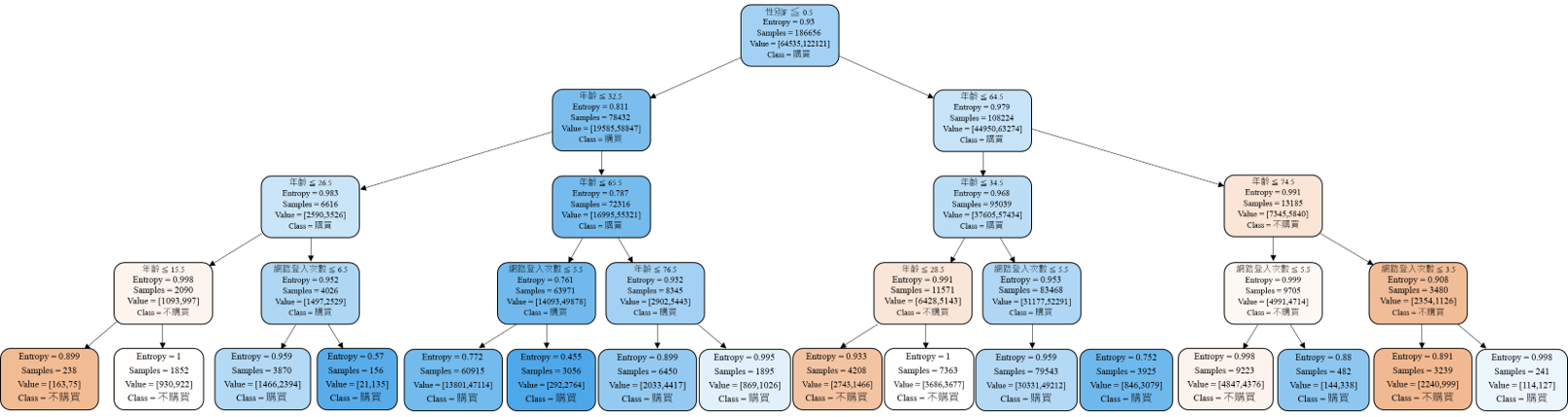
決策樹

決策樹

Usage
rpart(formula, data, weights, subset, na.action = na.rpart, method, model = FALSE, x = FALSE, y = TRUE, parms, control, cost, …)

Argument 

method : one of "anova", "poisson", "class" or "exp". If method is missing then the routine tries to make an intelligent guess. If y is a survival object, then method = "exp" is assumed, if y has 2 columns then method = "poisson" is assumed, if y is a factor then method = "class" is assumed, otherwise method = "anova" is assumed. It is wisest to specify the method directly, especially as more criteria may added to the function in future.
parms : optional parameters for the splitting function. Anova splitting has no parameters. Poisson splitting has a single parameter, the coefficient of variation of the prior distribution on the rates. The default value is 1. Exponential splitting has the same parameter as Poisson. For classification splitting, the list can contain any of: the vector of prior probabilities (component prior), the loss matrix (component loss) or the splitting index (component split). The priors must be positive and sum to 1. The loss matrix must have zeros on the diagonal and positive off-diagonal elements. The splitting index can be gini or information. The default priors are proportional to the data counts, the losses default to 1, and the split defaults to gini.
fit2 <- rpart(Kyphosis ~ Age + Number + Start, data = kyphosis,
              parms = list(prior = c(.65,.35), split = "information"))
Example:
prior probabilities

決策樹

Usage
rpart(formula, data, weights, subset, na.action = na.rpart, method, model = FALSE, x = FALSE, y = TRUE, parms, control, cost, …)

Argument 

control : a list of options that control details of the rpart algorithm. See 
rpart.control

超參數 hyperparameter

參數：就是模型可以根據數據自動學習出的變量就是參數。比如，深度學習的權重，偏差等

超參數：就是用來確定模型的一些參數，超參數不同，模型是不同的(這個模型不同的意思就是有微小的區別，比如假設都是CNN模型，如果層數不同，模型不一樣，雖然都是CNN模型。)，超參數一般就是根據經驗確定的變量。在深度學習中，超參數有：學習速率，迭代次數，層數，每層神經元的個數等等。


Source: https://blog.csdn.net/UESTC_C2_403/article/details/77428736

決策樹

Usage
rpart.control(minsplit = 20, minbucket = round(minsplit/3), cp = 0.01, maxcompete = 4, maxsurrogate = 5, usesurrogate = 2, xval = 10, surrogatestyle = 0, maxdepth = 30, …)

Argument 

minsplit : the minimum number of observations that must exist in a node in order for a split to be attempted.

minbucket : the minimum number of observations in any terminal <leaf> node. If only one of minbucket or minsplit is specified, the code either sets minsplit to minbucket*3 or minbucket to minsplit/3, as appropriate.
cp : complexity parameter. Any split that does not decrease the overall lack of fit by a factor of cp is not attempted. For instance, with anova splitting, this means that the overall R-squared must increase by cp at each step. The main role of this parameter is to save computing time by pruning off splits that are obviously not worthwhile. Essentially,the user informs the program that any split which does not improve the fit by cp will likely be pruned off by cross-validation, and that hence the program need not pursue it.

xval : number of cross-validations.

maxdepth : Set the maximum depth of any node of the final tree, with the root node counted as depth 0. Values greater than 30 rpart will give nonsense results on 32-bit machines.
minsplit : 每一個節點最少要有幾筆觀測值才會分裂。
minbucket :分裂出來的葉子至少要有幾筆觀測值。
cp: 決定精度的參數。
maxdepth : 樹的深度

決策樹

一般分類決策樹重要參數:

split: 通常就兩種 Entropy 或是 gini，維度大，噪音大使用吉尼係數。 但是，哪一個好，其實說不準，都試試選最佳的就好。

maxdepth: 最有效的剪枝手法，可以防止過擬合。通常看數據量決定最大深度。

minsplit: 分枝後的每個子節點必須包含多少個樣本。一般會搭配maxdepth使用。設置太小會引起過擬合，設置太大會限制模型學習。

minbucket: 要有多少訓練樣本才會分裂節點。

cp : 限制訊息增益的大小，信息增益小於設定數值的分支不會發生。但會隨method不同信息指標不同。主要為了更有效率訓練模型。

SKlearn中分類決策樹的重要參數詳解

隨機森林

隨機森林就是許多許多的決策樹模型重複的對欄位以及訓練集抽樣並行訓練模型最後以加權平均方式輸出最終模型。

這就是集成學習　Ensemble Learning 的概念之一。

採樣

n sample
n sample
n sample
n sample
n sample
n sample

...

...

...

訓練

...

...

子學習器
子學習器
子學習器
子學習器
子學習器
子學習器

平均

最終模型
N
Obs

隨機森林

集成學習有很多種，隨機森林是屬於其中的Bagging。

 

Bagging 是什麼?

  Bagging 又稱 Bootstrap Aggregating，簡單來說就是不斷採樣又放回，每次採樣相同數量，並且訓練出很多個強模型再將它們組合成一個最終學習器的方法。

 

集成學習中，還有很多類型， bagging只是一種 還有boosting 以及 stacking...等。

隨機森林

隨機森林

Usage
## S3 method for class 'formula': 
randomForest(formula, data=NULL, subset, ...) 
## S3 method for class 'default': 
randomForest(x, y=NULL, addclass=0, ntree=100, mtry=ceiling(sqrt(ncol(x))), classwt=NULL, nodesize=1, importance=FALSE, proximity=FALSE, outscale=FALSE, norm.votes=TRUE, do.trace=FALSE, ...)

Argument 

ntree : Number of trees to grow. This should not be set to too small a number, to ensure that every input row gets predicted at least a few times.
mtry : Number of variables randomly sampled as candidates at each split.
nodesize : Minimum size of terminal nodes. Setting this number larger causes smaller trees to be grown (and thus take less time).
importance : Should importance of predictors be assessed?

do.trace : If set to TRUE, give a more verbose output as randomForest is run.

我個人非常喜歡隨機森林因為限制少，參數不怎麼需要調整就能達到蠻好的成效。

隨機森林

那對於randomForest這個包裡面的隨機森林模型，有一個方便解釋模型的好套件，叫做 randomForestExplainer。
iris.rf <- randomForest::randomForest(Species ~ ., data=iris, localImp = TRUE)
require(randomForestExplainer)
explain_forest(iris.rf, interactions = TRUE, data = iris)
Example:
web link

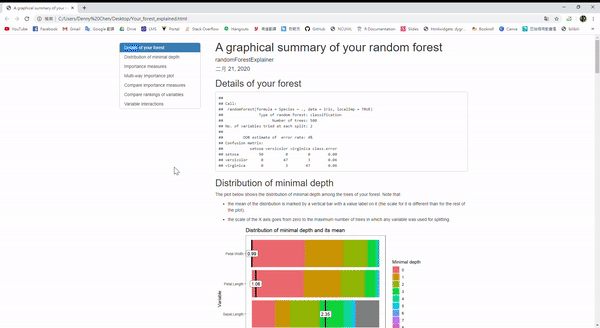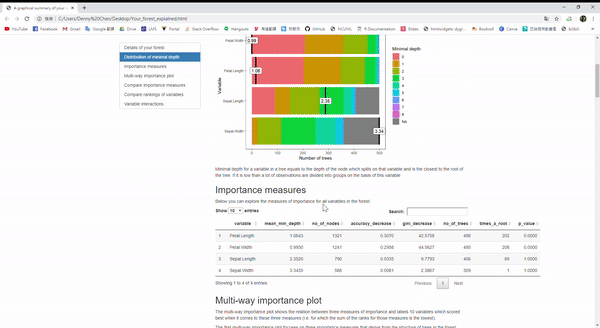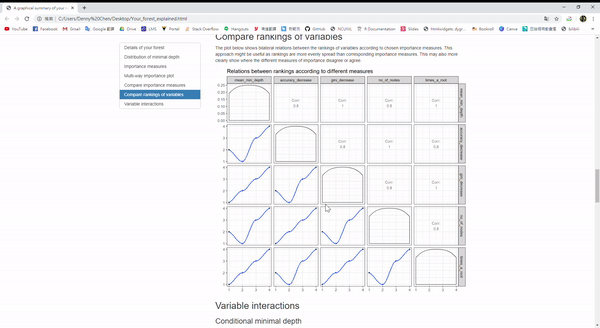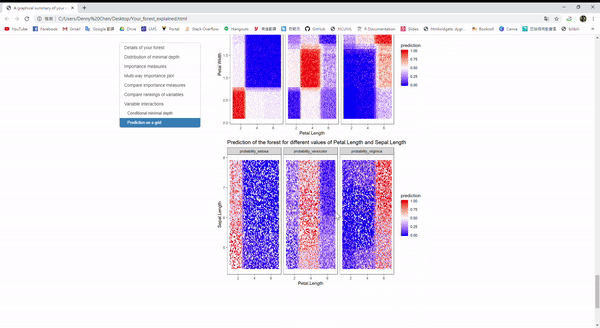
隨機森林

不過! randomForest通常會訓練較久的時間，因此有一個超強大又有效率的隨機森林套件叫做 ranger。

Boosting淺談

我們來談談集成學習的另一個類型 Boosting，跟 Bagging 使用多個「強模型」不同， Boosting 會強調使用上需要多個「弱模型」才可以。

 

其概念用「三個臭皮匠，勝過一個諸葛亮」來形容最為貼切，也就是需要有多個非常弱的「臭皮匠」，而這些臭皮匠彼此是互補的。也就是說： M2 模型要能辦到 M1 模型所辦不到的， M3 要辦到 M2 所辦不到的……。

 

所以，Boosting算法跟隨機森林不一樣在於他不是並行訓練模型，而是一次又一次的迭代訓練，而每一次跟前一次會因訓練出的模型不同而有不同的算法。

 

那今天就主要介紹:

 

 

 

 

      

XGboost
ADAboost

                     極限梯度提升                                                                                自適應增強

Boosting淺談

                     極限梯度提升                                                                                自適應增強

XGboost
ADAboost

每一次建模會將分錯的樣本權重提高，降低已經正確分類樣本的權重，讓模型更注重那些沒有被正確分類的樣本，並將本次模型分錯的樣本以及其他新數據構成新的相同數量樣本以訓練下一個模型，...以此類推下去，最終得到很多弱分類器，並根據弱分類器的多數投票表決。

每一次建模對於模型來說就是學習一個新的函數，並且以第n個模型去擬合n-1個模型預測的殘差。訓練完K個弱學習器，要預測新樣本時，模型會根據這個樣本的特徵，將這個樣本落到每一棵樹對應的葉子節點，每一個葉子節點會對應到一個分數，最後將每一棵樹相應的分數相加起來就是該樣本的預測值。

優點:

1. 很好利用弱分類器聯集

2. 可以將不同的分類算法作為分類器

3. 具有很高的精度

4. 充分考慮每個分類器的權重

缺點:

1. 弱分類器數目不好設定

2. 數據不平衡導致精度下降

3. 對於異常值敏感

4. 訓練比較耗時

優點:

1. 損失函數中加入正則項控制模型複雜度，並避免過擬合的發生。

2. 支援並行處理(特徵粒度上面)(並非同時訓練很多樹)。

3. 靈活度高(自定義目標與損失函數，只要目標二階可導)

4. 隊友特徵的值有缺失的樣本可以自行學習出分枝方向。

5. 自動剪枝不容易陷入區域最佳解。

6. 內建交叉驗證。

缺點:

1. 調參困難，參數過多。

2. 只適合處理結構化資料。

3. 訓練有夠久= =

SVM

SVM是一種監督式的學習方法，用統計風險最小化的原則估計一個分類的最佳超平面(hyperplane)，其基礎的概念非常簡單，就是找到一個決策邊界，讓兩類之間的邊界margins最大化，使其可以最佳區隔開來。

height
weight
Boys
Girls
Optimal hyperplane

SVM

SVM的分類就是找出可以將兩類資料分開最遠的那條線

}

也就是Margins最大

height
weight
Boys
Girls
Support Vectors

SVM

但現實資料不可能會那麼乾淨的剛好分成兩邊。這時候就需要來談談 Kernel，SVM的靈魂。 

 

那什麼是Kernel核函數?

當資料無法以線性函數來區分時就需要將資料映射到特徵空間所使用到的函數。

Kernel 主要有四種函數:

1. 線性 Linear   2. 多項式 Polynomial  3. 徑向基函數核 Radial Basis Function 4. 雙彎曲 Sigmoid

SVM

我們舉一個用Polynomial kernel function，次方項為2次，截距為0的例子。

右邊很明顯圈內一類，圓圈一類，沒有辦法用線性函數來區分，因此我們要找一個非線性分類器讓兩者分開。

這邊的kernel function比較簡單:

 

 

經由推導得到投影函數(φ)，如下:

 

 

 

 

 

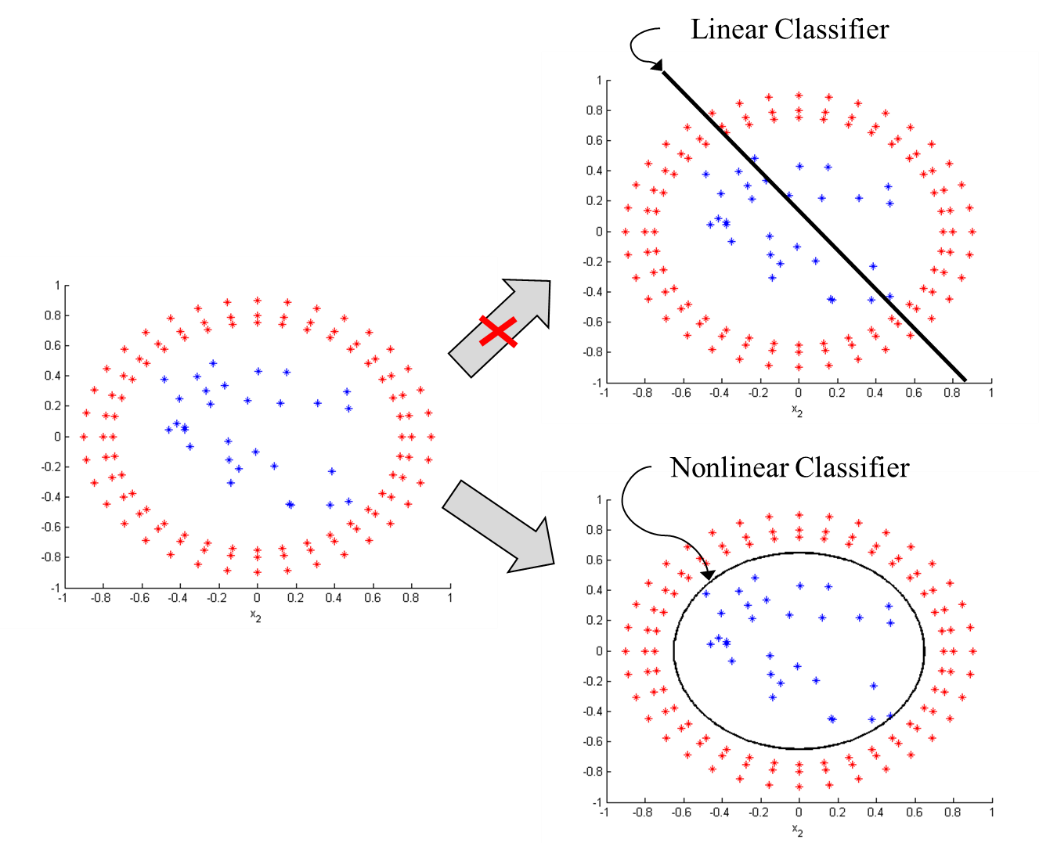
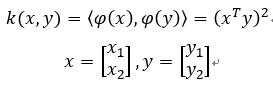
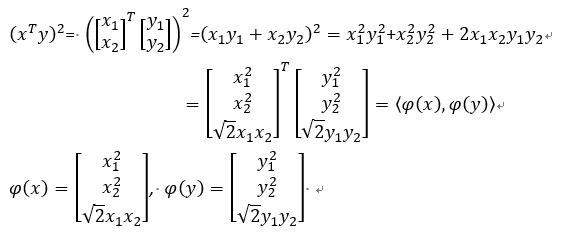
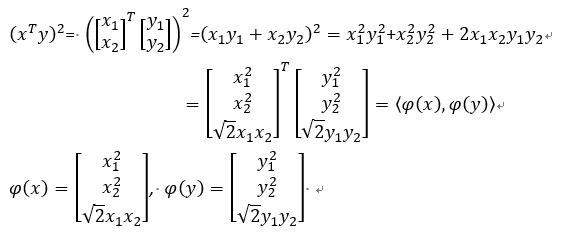
因此，我們可以看到用polynomial kernel function將資料投影到feature space後的情況，將資料由2維空間轉換為3維空間。

 

SVM

因此，我們可以看到用polynomial kernel function將資料投影到feature space後的情況，將資料由2維空間轉換為3維空間。

這時候，很明顯只要一個超平面就可以完美分類。

SVM

上面用的polynomial轉換成投影函數(φ)比較簡單，這邊繼續介紹 Radial Basis function ( RBF kernel function)。

RBF的話，會用到泰勒級數: (忘記的回憶一下)

e^x =\sum_{n=0}^{\infty} \frac{x^n}{n!}

RBF Kernel function 會用到的泰勒級數是

下面舉一個一維的例子:

我們可以知道，如果RBF要轉換到更高維度的空間是看泰勒級數要展開幾層，如果資料2維，要再3維空間看RBF轉換就要展到0~2階，投影函數(φ)的每一個元素(element)公式如下:

e_n(x)=\sqrt{\frac{(2\sigma)^n}{n!}}{x^n}{e^{-\sigma x^2}}, n = 0,1,2,...

SVM

延續剛剛的例子，2維資料用RBF kernel function拆解出的投影函數(φ):

下圖可以看到RBF如何將2維資料投影到3維空間上

Kernel的手法只是將資料投到更高維度的空間，然後在這高維度的空間進行你想做的事情，不一定要直接在高維度空間做分類(此例是在高維度空間分類)，也可以在高維度空間進行降維(dimension reduction)，關鍵字kernel PCA, kernel LDA。

click for more detail

SVM

SVM

Usage
# S3 method for formula 
svm(formula, data = NULL, ..., subset, na.action = na.omit, scale = TRUE) 
# S3 method for default 
svm(x, y = NULL, scale = TRUE, type = NULL, kernel = "radial", degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x), coef0 = 0, cost = 1, nu = 0.5, class.weights = NULL, cachesize = 40, tolerance = 0.001, epsilon = 0.1, shrinking = TRUE, cross = 0, probability = FALSE, fitted = TRUE, ..., subset, na.action = na.omit)

Argument 

x:可以是矩陣，可以是向量，也可以是稀疏矩陣
y:分類變量
type:指定建模的類別，支持向量機通常用於分類、回歸和異常值檢測，默認情況下，svm模型根據因變量y是否為因子，type選擇C-classification或eps-regression
kernel:指定建模過程中使用的核函數，目的在於解決支持向量機線性不可分問題。
degree:用於多項式核函數的參數，默認為3
gamma:用於除線性核函數之外的所有核函數參數，默認為1
coef0:用於多項式核函數和神經網絡核函數的參數，默認為0
cost: 懲罰係數，即對誤差的寬容度。C越高，說明越不能容忍出現誤差,容易過擬合。C越小，容易欠擬合。C過大或過小，泛化能力變差
class.weights:指定類權重
cachesize:默認緩存大小為40M
epsilon: SVR才會用到的參數
cross:可為訓練集數據指定k重交叉驗證
probability:邏輯參數，指定模型是否生成各類的概率預測，默認不產生概率值

1. If you have a classification problem, i.e., discrete label to predict, you can use C-classification and nu-classification.
2. If you have a regression problem, i.e., continuous number to predict, you can use eps-regression and nu-regression.
3. If you only have one class of the data, i.e., normal behavior, and want to detect outliers. one-classification.

SVM

gamma: defines how far the influence of a single training example reaches

RBF公式裏面的sigma和gamma的關系如下：
簡單來說，當gamma愈大，RBF裡面的 σ就越小，導致高斯分布峰度越大。只有Margins邊界附近的樣本有影響力。gamma越大，模型越容易過擬合。
low gamma values - far inflence

離決策邊界遠的點也有影響力，使模型的決策邊界會受到那些遠的點的影響
high gamma values - close inflence

離決策邊界遠的點影響力低，使模型的決策邊界只會受到近的點的影響，而更傾向將中間分更開

結論

gamma大，資料點的影響力範圍比較近，對超平面來說，近點的影響力權重較大，容易勾勒出擬合近點的超平面，也容易造成overfitting。

gamma小，資料點的影響力範圍比較遠，對超平面來說，較遠的資料點也有影響力，因此能勾勒出平滑、近似直線的超平面。

SVM

SVM

tune.svm(Species ~., data =iris, gamma = 10^(-100:-1), cost = 10^(0:3))
Example:

Learn R  |  SVM of Data Mining（五） - Jason的文章 - 知乎

Link:

那怎麼知道參數設定多少最好呢?  其實今天所講的所有參數都沒有一定規則。情況都會視資料不同，目的不同而有所差異。

講明白就是經驗談，用多了用久了自然就會有概念了，就連我也抓不準，那怎麼辦?

有一個辦法就是                     !

GridSearch
GridSearch 就是超參數優化(Hyperparameter Optimization)中的一種手段:

窮舉
也就是將所有的參數配對都放入模型訓練在選出表現最佳的

caret package

等等會用caret套件，開始前大家可以先安裝好

install.packages("caret")

caret
Classification And REgression Training

CRAN pdf

caret

> names(caret::getModelInfo())

  [1] "ada"                 "AdaBag"              "AdaBoost.M1"        
  [4] "adaboost"            "amdai"               "ANFIS"              
  [7] "avNNet"              "awnb"                "awtan"              
 [10] "bag"                 "bagEarth"            "bagEarthGCV"        
 [13] "bagFDA"              "bagFDAGCV"           "bam"                
 [16] "bartMachine"         "bayesglm"            "binda"              
 [19] "blackboost"          "blasso"              "blassoAveraged"     
 [22] "bridge"              "brnn"                "BstLm"              
 [25] "bstSm"               "bstTree"             "C5.0"               
 [28] "C5.0Cost"            "C5.0Rules"           "C5.0Tree"           
 [31] "cforest"             "chaid"               "CSimca"             
 [34] "ctree"               "ctree2"              "cubist"             
 [37] "dda"                 "deepboost"           "DENFIS"             
 [40] "dnn"                 "dwdLinear"           "dwdPoly"            
 [43] "dwdRadial"           "earth"               "elm"                
 [46] "enet"                "evtree"              "extraTrees"         
 [49] "fda"                 "FH.GBML"             "FIR.DM"             
 [52] "foba"                "FRBCS.CHI"           "FRBCS.W"            
 [55] "FS.HGD"              "gam"                 "gamboost"           
 [58] "gamLoess"            "gamSpline"           "gaussprLinear"      
 [61] "gaussprPoly"         "gaussprRadial"       "gbm_h2o"            
 [64] "gbm"                 "gcvEarth"            "GFS.FR.MOGUL"       
 [67] "GFS.LT.RS"           "GFS.THRIFT"          "glm.nb"             
 [70] "glm"                 "glmboost"            "glmnet_h2o"         
 [73] "glmnet"              "glmStepAIC"          "gpls"               
 [76] "hda"                 "hdda"                "hdrda"              
 [79] "HYFIS"               "icr"                 "J48"                
 [82] "JRip"                "kernelpls"           "kknn"               
 [85] "knn"                 "krlsPoly"            "krlsRadial"         
 [88] "lars"                "lars2"               "lasso"              
 [91] "lda"                 "lda2"                "leapBackward"       
 [94] "leapForward"         "leapSeq"             "Linda"              
 [97] "lm"                  "lmStepAIC"           "LMT"                
[100] "loclda"              "logicBag"            "LogitBoost"         
[103] "logreg"              "lssvmLinear"         "lssvmPoly"          
[106] "lssvmRadial"         "lvq"                 "M5"                 
[109] "M5Rules"             "manb"                "mda"                
[112] "Mlda"                "mlp"                 "mlpKerasDecay"      
[115] "mlpKerasDecayCost"   "mlpKerasDropout"     "mlpKerasDropoutCost"
[118] "mlpML"               "mlpSGD"              "mlpWeightDecay"     
[121] "mlpWeightDecayML"    "monmlp"              "msaenet"            
[124] "multinom"            "mxnet"               "mxnetAdam"          
[127] "naive_bayes"         "nb"                  "nbDiscrete"         
[130] "nbSearch"            "neuralnet"           "nnet"               
[133] "nnls"                "nodeHarvest"         "null"               
[136] "OneR"                "ordinalNet"          "ordinalRF"          
[139] "ORFlog"              "ORFpls"              "ORFridge"           
[142] "ORFsvm"              "ownn"                "pam"                
[145] "parRF"               "PART"                "partDSA"            
[148] "pcaNNet"             "pcr"                 "pda"                
[151] "pda2"                "penalized"           "PenalizedLDA"       
[154] "plr"                 "pls"                 "plsRglm"            
[157] "polr"                "ppr"                 "PRIM"               
[160] "protoclass"          "qda"                 "QdaCov"             
[163] "qrf"                 "qrnn"                "randomGLM"          
[166] "ranger"              "rbf"                 "rbfDDA"             
[169] "Rborist"             "rda"                 "regLogistic"        
[172] "relaxo"              "rf"                  "rFerns"             
[175] "RFlda"               "rfRules"             "ridge"              
[178] "rlda"                "rlm"                 "rmda"               
[181] "rocc"                "rotationForest"      "rotationForestCp"   
[184] "rpart"               "rpart1SE"            "rpart2"             
[187] "rpartCost"           "rpartScore"          "rqlasso"            
[190] "rqnc"                "RRF"                 "RRFglobal"          
[193] "rrlda"               "RSimca"              "rvmLinear"          
[196] "rvmPoly"             "rvmRadial"           "SBC"                
[199] "sda"                 "sdwd"                "simpls"             
[202] "SLAVE"               "slda"                "smda"               
[205] "snn"                 "sparseLDA"           "spikeslab"          
[208] "spls"                "stepLDA"             "stepQDA"            
[211] "superpc"             "svmBoundrangeString" "svmExpoString"      
[214] "svmLinear"           "svmLinear2"          "svmLinear3"         
[217] "svmLinearWeights"    "svmLinearWeights2"   "svmPoly"            
[220] "svmRadial"           "svmRadialCost"       "svmRadialSigma"     
[223] "svmRadialWeights"    "svmSpectrumString"   "tan"                
[226] "tanSearch"           "treebag"             "vbmpRadial"         
[229] "vglmAdjCat"          "vglmContRatio"       "vglmCumulative"     
[232] "widekernelpls"       "WM"                  "wsrf"               
[235] "xgbDART"             "xgbLinear"           "xgbTree"            
[238] "xyf"

有哪些模型可以用

caret

有哪些參數可以調整

modelLookup(model = " ")
> modelLookup(model = "rpart")
  model parameter                label forReg forClass probModel
1 rpart        cp Complexity Parameter   TRUE     TRUE      TRUE
> modelLookup(model = "rpart2")
   model parameter          label forReg forClass probModel
1 rpart2  maxdepth Max Tree Depth   TRUE     TRUE      TRUE
> modelLookup(model = "rf")
  model parameter                         label forReg forClass probModel
1    rf      mtry #Randomly Selected Predictors   TRUE     TRUE      TRUE
> modelLookup(model = "ranger")
   model     parameter                         label forReg forClass probModel
1 ranger          mtry #Randomly Selected Predictors   TRUE     TRUE      TRUE
2 ranger     splitrule                Splitting Rule   TRUE     TRUE      TRUE
3 ranger min.node.size             Minimal Node Size   TRUE     TRUE      TRUE
> modelLookup(model = "xgbTree")
    model        parameter                          label forReg forClass probModel
1 xgbTree          nrounds          # Boosting Iterations   TRUE     TRUE      TRUE
2 xgbTree        max_depth                 Max Tree Depth   TRUE     TRUE      TRUE
3 xgbTree              eta                      Shrinkage   TRUE     TRUE      TRUE
4 xgbTree            gamma         Minimum Loss Reduction   TRUE     TRUE      TRUE
5 xgbTree colsample_bytree     Subsample Ratio of Columns   TRUE     TRUE      TRUE
6 xgbTree min_child_weight Minimum Sum of Instance Weight   TRUE     TRUE      TRUE
7 xgbTree        subsample           Subsample Percentage   TRUE     TRUE      TRUE

caret

caret

caret

caret

model <- train(formula = ,
               data = ,
               method = "",
               trControl = trainControl(method = "",
                                        number = , 
                                        repeats = , 
                                        search = , 
                                        verboseIter = , 
                                        classProbs = , 
                                        summaryFunction = , 
                                        allowParallel = ,
                                        sampling = ),
               preProcess = "", 
               tuneGrid = expand.grid(), 
               tuneLength = ,
               metric = "")

我們用train這個function來訓練模型。

下面是我平常會用到的一些引數。

caret package

實戰

caret package 實戰

library(tidyverse)
library(magrittr)

employee <- readr::read_csv("Employee.csv")

uniqlen <- sapply(employee, function(x) length(unique(x)))

drop_col <- names(uniqlen[uniqlen == 1])

employee %<>%
  select(-drop_col)

str(employee)

sapply(employee%>% select_if(is.character), function(x) length(table(x)))

employee %<>% mutate_if(is.character, as.factor)

library(caret)

n <- sample(nrow(employee), 0.8*nrow(employee))
trainset <- employee[n, ] %>% as.data.frame()
testset <- employee[-n, ] %>% as.data.frame()
model <- train(x = trainset[,-2],
               y = trainset[,2],
               data = trainset, 
               method = "rf", 
               trControl = trainControl(method = "cv", 
                                        number = 3, 
                                        verboseIter = T, 
                                        summaryFunction = twoClassSummary, 
                                        classProbs = T),
               tuneLength = 5,
               metric = "ROC")

result <- predict.train(model, newdata = testset, type = "raw")

caret::confusionMatrix(result, testset$Attrition)

THANKS

Made with Slides.com