Revisión - Junio 2019

DyCon Toolbox is a MATLAB library of Non Lineal Optimal  Control

\min_{u\in\Omega} J \\
s.t. \ \ \dot{Y} = f(t,Y,U) \\ s.t. \ \ Y(0) = Y_0
s.t. \ \ C(Y,U) = 0 \\ s.t. \ \ G(Y,U) < 0 \\

Dynamic

Constraint

Control State Constraints

J = \Psi(T,Y(T)) + \int_0^T L(t,Y(t),U(t)) dt \\

DyCon Toolbox solve this problem:

\min_{u\in\Omega} J \\
J = \Psi(T,Y(T)) + \int_0^T L(t,Y(t),U(t)) dt \\
s.t. \ \ \dot{Y} = f(t,Y,U) \\ s.t. \ \ Y(0) = Y_0
s.t. \ \ C(Y,U) = 0 \\ s.t. \ \ G(Y,U) < 0 \\

Dynamic

Constraint

Control State Constraints

With Final Time Fixed

DyCon Toolbox solve this problem:

Method Clasification to solve this problems

Indirect Methods

Direct Methods

Use the optimal conditions 

Discretization all equations

H = L + p*f \\ \dot{p} = -H_{y} \\ \dot{x} = H_{p} \\ H_{u} = 0 \\ ...
U = [u_1 u_2 \ ... \ u_3] \\ Y = [y_1 y_2 \ ... \ y_3]
\min \ J(u_1,u_2,...,y_1,y_2)

Methods to solve this problem

AMPL IPOPT

H = L + p*f \\ \dot{p} = -H_{y} \\ \dot{x} = H_{p} \\ H_{u} = 0 \\ ...
U = [u_1 u_2 \ ... \ u_3] \\ Y = [y_1 y_2 \ ... \ y_3]
\min \ J(u_1,u_2,...,y_1,y_2)

Indirect Methods

Direct Methods

DyCon Toolbox puede obtener las condiciones de optimalidad gracias al cálculo simbólico de MATLAB

Indirect Methods

Indirect Methods

J = y_1^2(1) + y_2^2(1) + 0.005*\int_0^1 u_1^2(t) + u_2^2(t) dt \\
\begin{bmatrix} \dot{y_1} \\ \dot{y_2} \\ \end{bmatrix} = \begin{bmatrix} y_1y_2 + u_1 \\ -y_2 +u_2 \\ \end{bmatrix}
\begin{bmatrix} y_1(0) \\ y_2(0) \\ \end{bmatrix} = \begin{bmatrix} 0 \\ -1 \\ \end{bmatrix}

Veamos un ejemplo

Y = sym('y',[2 1]); U = sym('u',[1 1])
% Vector dynamics
F = @(t,Y,U) [      Y(1)*Y(2)  + U(1)   ; ...
                   -Y(2)       + U(2) ] ;
% Create a ode object
dynamics = ode(F,Y,U);
dynamics.InitialCondition = [0;-1];
%
Psi = @(T,Y)   Y*Y;
L   = @(t,Y,U) 0.005*(U*U) ;
%
% We finally define the optimal control problem as a 
% Pontryagin class:
iP = Pontryagin(dynamics,Psi,L);
%

Indirect Methods

En código ...

Indirect Methods

\partial_Y f(t,Y,U) \\ \partial_U f(t,Y,U) \\ \partial_Y L(t,Y,U) \\ \partial_U L(t,Y,U) \\ \partial_Y \Psi(T,Y(T))

Con estos pasos hemos obtenido la expresión simbólica y el función numérica de: 

Indirect Methods

\partial_Y f(t,Y,U) \\

Por ejemplo:

>> iP.Dynamics.DerivativeDynState

ans = 

  SymNumFun with properties:

     Numerical: @(t,in2,in3)reshape([in2(2,:),0.0,in2(1,:),-1.0],[2,2])
    Symbolical: [2×2 sym]

Si vemos en el interior de la variable IP encontramos la expresión simbólica y la función numérica 

Indirect Methods

\partial_Y f(t,Y,U) \\

Por ejemplo:

>> iP.Dynamics.DerivativeDynState.Symbolical
 
ans =
 
[ y2, y1]
[  0, -1]

Vemos en este caso el valor simbólico

\begin{bmatrix} \dot{y_1} \\ \dot{y_2} \\ \end{bmatrix} = f(t,Y,U) = \begin{bmatrix} y_1y_2 + u_1 \\ -y_2 +u_2 \\ \end{bmatrix}
\partial_Y f = \begin{bmatrix} y_2 & y_1 \\ 0 & -1 \\ \end{bmatrix}

Indirect Methods

\dot{P} = \partial_Y f + \partial_Y L \\ s.t. \ \ P(T) = \partial_Y \Psi

De la misma forma para Adjoint Equation

\text{Dado que tenemos }\partial_Y f \text{ y } \partial_Y L \text{ podemos calcular } \\ \text{ la ecuación adjunta}

Indirect Methods

\text{Give } U \rightarrow \text{ Obtain }[J, d_{U}J, d^2_{U}J]

DyCon Toolbox resume todo a una función

>> [J,Gradient,Hessian] = Control2Functional(iP,U0)
J =

    0.1200


Gradient =

   -0.0240         0
   -0.0270         0
   -0.0304         0
   -0.0342         0
   -0.0384         0
   -0.0433         0
   -0.0487         0
   -0.0547         0
   -0.0616         0
   -0.0693         0


Hess =

         0   -1.0000
         0   -0.8889
         0   -0.7901
         0   -0.7023
         0   -0.6243
         0   -0.5549
         0   -0.4933
         0   -0.4385
         0   -0.3897
         0   -0.3464

Indirect Methods

\text{Give } U \rightarrow [J, d_{U}J, d^2_{U}J]

Se han implementado métodos del gradiente dentro de DyCon Toolbox

GradientMethod(iP,U0,'DescentAlgorithm',@ConjugateDescent) 
%
GradientMethod(iP,U0,'DescentAlgorithm',@ClassicalDescent)
%
GradientMethod(iP,U0,'DescentAlgorithm',@AdaptativeDescent)

Indirect Methods

\text{Give } U \rightarrow [J, d_{U}J, d^2_{U}J]

Además se puede acoplar fácilmente con el optimizador fmincon de MATLAB

Umax =  1;
Umin = -1;
fmincon(@(U)Control2Functional(iP,U),U0,      ... % U0 initial guess
                                   [],[],     ... % A*U = 0
                                   [],[],     ... % A*U > 0
                                   Umin,Umax, ... % Umin<U<Umax 
                                   []);       ... % G(U) < 0

Indirect Methods

Resolución de ODE

Tanto en el cálculo de la dinámica directa como en la dinámica adjunta se debe resolver una ODE.

Esta pieza del algoritmo es intercambiable. Lo más importante es que tenga una interfaz determinada.

Indirect Methods

Herramientas las ODE

% DyCon Toolbox Syntax
Y = sym('y',[2 1]); U = sym('u',[1 1])
% Vector dynamics
F = @(t,Y,U) [      Y(1)*Y(2)  + U(1)   ; ...
                   -Y(2)       + U(2) ] ;
% Create a ode object
dynamics = ode(F,Y,U);
dynamics.Solver = @ode45
% Interfaz Obligatoria
dynamics.InitialCondition = [0;-1];
[tspan ,Ysolution] = solve(dynamics)

Indirect Methods

Diferentes Solvers

  • ode45 - MATLAB implentation
  • ode23 - MATLAB implentation
  • ode23tb - MATLAB implentation
  • rk4 - simple 
  • eulere - simple
  • euleri  - simple
% change the solver
dynamics.Solver = @ode45

Indirect Methods

Herramientas específicas 

  • HUM - Implementación de Umberto y Víctor del método del gradiente para problemas lineales sin restricciones 
  • LQR - Implementación de Dario, utilizando las herramientas de MATLAB para problemas LQR
  • InverseProblem - Implementacion de Azahar de Problemas tipo:
\min_{Y(0)} J \\ J = \int ( y(T) - y_{Target}) dx + \gamma \int |y(0)| dx \\ s.t. \ \ \dot{y} = A*y \ \
  • LsNorm - Implementacion de Umberto para problemas tipo:
\min_{U} J \\ J = ||Y(T) - Y_T||_{L^2} + \gamma \int || U ||_{L^s}dt \\ s.t. \ \ \dot{Y} = A*Y + B^U\ \

Posibles Extensiones

Posibles Extensiones

Desarrollar un método propio para discretizar todo el problema, y calcular sus derivadas discretas (como AMPL)

Dentro del la clase Pontryagin tenemos todo lo necesario para poder calcular las derivadas discretas.

Esto nos ayudaría a extender Dycon Toolbox a métodos indirectos

AMPL IPOPT

Indirect Methods

Direct Methods

Posibles Extensiones

Desarrollar un método propio para discretizar todo el problema, y calcular sus derivadas discretas (como AMPL)

Dentro del la clase Pontryagin tenemos todo lo necesario para poder calcular las derivadas discretas.

Esto nos ayudaría a extender Dycon Toolbox a métodos indirectos

Indirect Methods

Direct Methods

AMPL IPOPT

Posibles Extensiones

Acoplar con IPOPT

El enlace con FMINCON de MATLAB esta hecho pero este tipo de problemas funcionan mejor con los métodos directos (Problemas totalmente discretizado)

Posibles Extensiones

Crear tutoriales sobre problemas clásicos: braquistocrona,  Principio de Fermat, ...

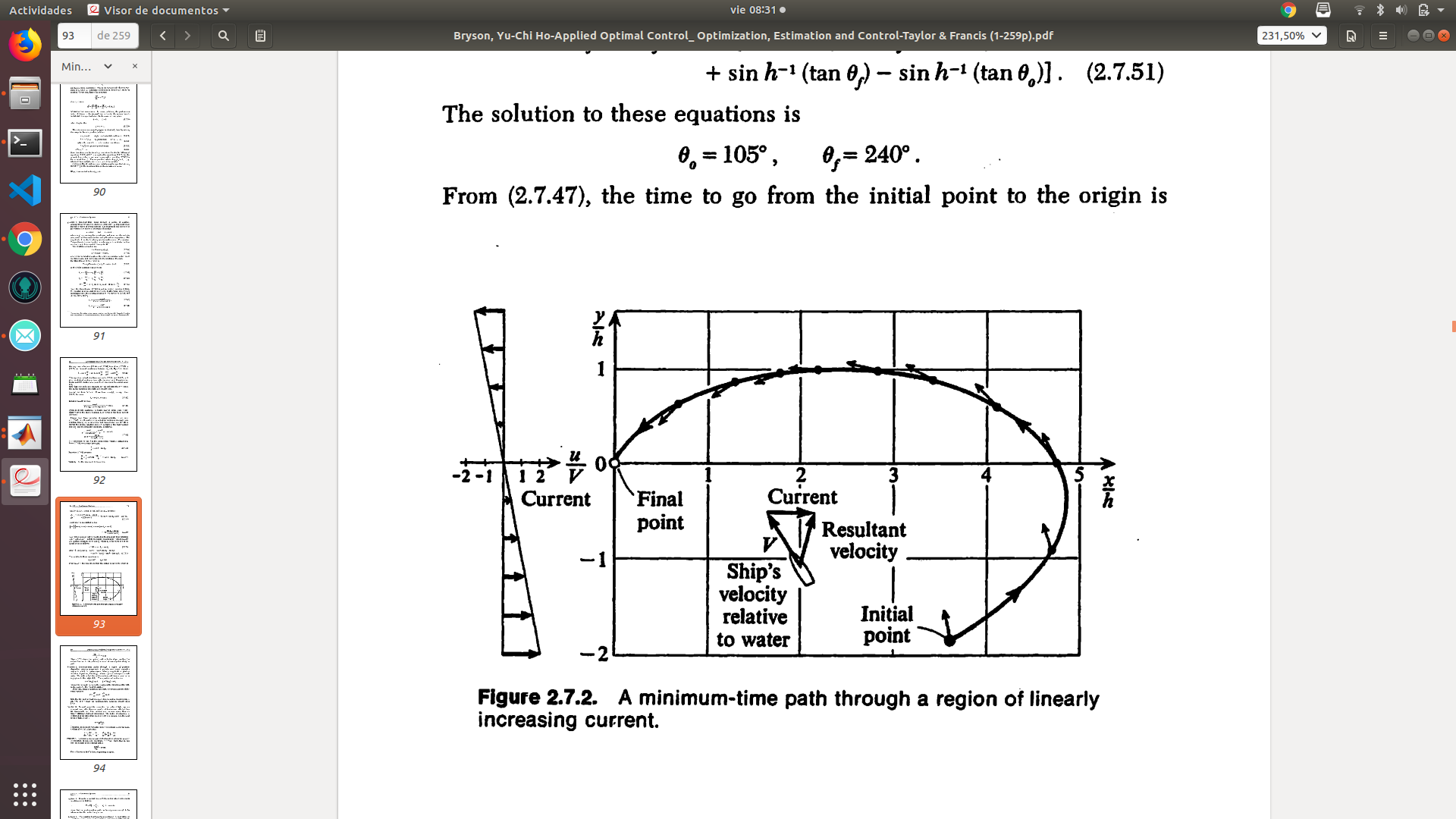
Posibles Extensiones

Agregar los métodos del gradiente que permiten un tiempo final variable

Book:   Applied Optimal Control: Optimization Estimation and Control

Posibles Extensiones

Utilizar PDE Toolbox en MATLAB. Solo para obtener las matrices de Mass, Stiffnex, ...

  • K is the stiffness matrix, the integral of the c coefficient against the basis functions.

  • M is the mass matrix, the integral of the m or d coefficient against the basis functions.

  • A is the integral of the a coefficient against the basis functions.

  • F is the integral of the f coefficient against the basis functions.

  • Q is the integral of the q boundary condition against the basis functions.

  • G is the integral of the g boundary condition against the basis functions.

  • The H and R matrices come directly from the Dirichlet conditions and the mesh.

FEM = assembleFEMatrices(model)

Posibles Extensiones

Utilizar PDE Toolbox en MATLAB. Solo para obtener las matrices de la dinámica

Heat Equation with some no lineal term  in DyCon Logo

Posibles Extensiones

Añadir funcionalidades desarrolladas en el proyecto Elkartek

Umberto esta implementado de forma independiente junto Mondragon, métodos para buscar regiones de estabilidad.

La sintaxis de los scripts son muy compatibles con la sintaxis para definir ODE en DyCon Toolbox

Dado una dinámica y un punto de estabilidad, recuperan una región de estabilidad.

Posibles Extensiones

Tareas y Personas

Persona Tarea
Dario Desarrollar un método propio para discretizar todo el problema, y calcular sus derivadas discretas (como AMPL)
Domenec Utilizar PDE Toolbox en MATLAB. Solo para obtener la función de la dinamicas
Umberto Proyecto Elkartek
Dongnam Optimización de la arquitectura de software, y testeo 
? Problemas Clásicos
Made with Slides.com