Redes Neuronales
redes neuronales anticipativas - neuronas artificales
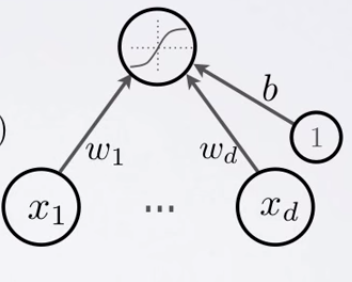
Neurona Artificial
Tópicos: pesos de conexión, sesgo (bias), función de activación
- Pre Activación neuronal ( o activación de entradas)
a( \mathbf{x} ) = b + \sum_i w_i x_i = b + \mathbf{w}^T \mathbf{x}
- Activación neuronal (salida)
h(\mathbf{x}) = g(a(\mathbf{x})) = g( b + \sum_i w_i x_i )
- W pesos de las conexiones
- b sesgo de la neurona
- g() función de activación
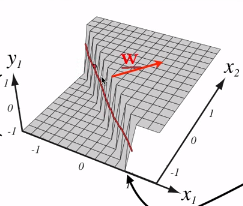
Neurona Artificial
Rango determinado por
g( \cdot ) \lbrace
funciones de activación
función de activación lineal
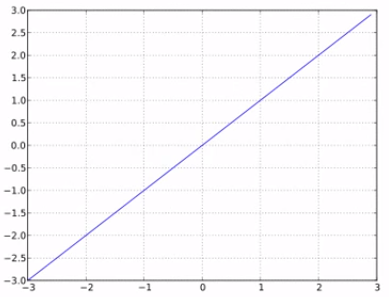
g(a) = a
- No realiza ningún aplastamiento de los datos
- No muy interesante
funciones de activación
función de activación sigmoide
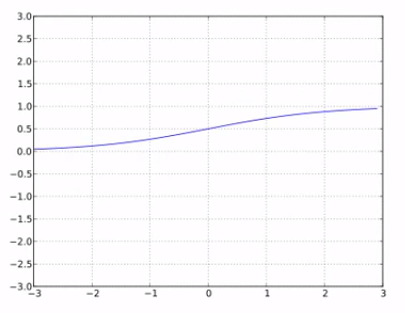
g(a) = sigm (a) = \frac{1}{1 + e^{-a} }
- Realiza aplastamiento de los datos entre 0 y 1
- Siempre positiva
- Acotada
- Estrictamente creciente