Задача за училищен график

Димитрина Златкова, 61610

Извличане на знания от данни, 2015

(School Timetabling Problem)

Какво?

• задача за удовлетворяване на ограниченията
• NP-пълна
• популярна в сферата на компютърните науки

• 13 учителя
• 13 учебни предмета
• 6 групи от ученици (паралелки)
• 5 учебни дни на седмица
• 7 времеви интервала

Как?

SAT = Boolean satisfiability problem = задача за удовлетворяване на булеви ограничения

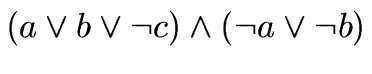
• Конюнктивна нормална форма

променливи

ограничения

(клаузи)

= True

?

Променливи

Lesson

• day
• number
• group
• subject

Mon..Fri

1..7

A..F

Maths

English

History

Sport

...

Oграничения (1)

Задължителни (hard constraints):

• Един учител води най-много един учебен час в даден времеви интервал.

• Една група от ученици присъства в най-много един учебен час в даден времеви интервал.

• Всяка група от ученици има занятия по даден предмет толкова пъти през седмицата, колкото е предвидено в програмата ѝ.

• Всяка група от ученици има занятия по един и същи предмет най-много веднъж на ден.

Препоръчителни (soft constraints):

• Даден учител иска да води занятия само през сутрешните/обедните часове.

• Даден учител иска да води всичките си занятия в конкретен ден/дни от седмицата.

• Даден учител не иска да води повече от N занятия на ден.

• Даден учител не иска да води занятия в конкретен ден/дни от седмицата.

Oграничения (2)

• Java библиотека
• отворен код (GNU LGPL лиценз)
• широко приложение
• Eclipse я използва за управление на зависимостите между пакетите

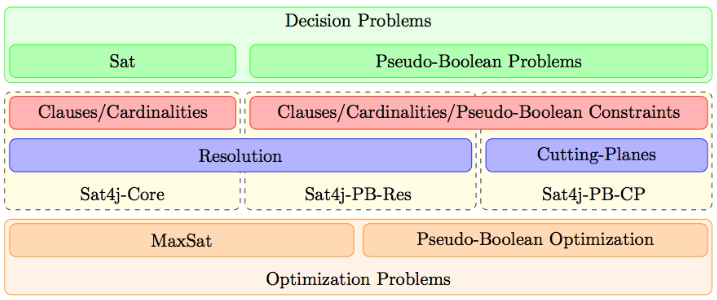
Conflict-Driven Clause Learning

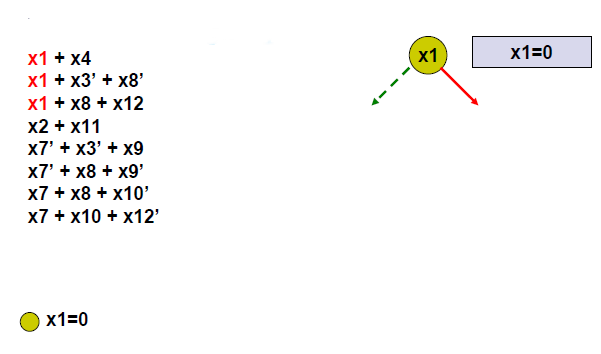
1. Избира променлива и я определя като True/False.

Conflict-Driven Clause Learning

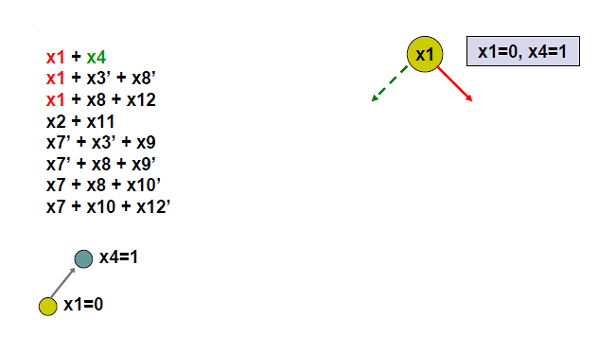
2. Разпространява булевото ограничение.

Строи граф на импликациите.

Conflict-Driven Clause Learning

3. При намерен конфликт добавя клауза за него.

Conflict-Driven Clause Learning

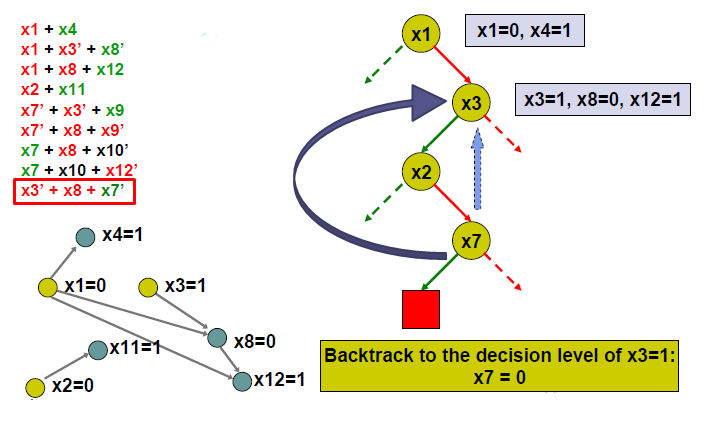
4. Връща се до подходящо ниво на решение (non-chronological backtracking).

• void atMost(C name, int n, Т... things)
• void atLeast(C name, int n, Т... things)
• void setFalse(Т thing, C name)
• void setTrue(Т thing, C name)
• ...

DependencyHelper<T,C>

• day
• number
• group
• subject

Програмиране на ограниченията(1)

for (Day day : Day.values()) {
    for (int number = 1; number <= lessonsADay; number++) {
	for (Subject subject : Subject.values()) {

	    Lesson[] groups = lessonCombinations
		        	.stream()
				.filter(l -> 
                                            l.getDay().equals(day) 
                                            && l.getNumber() == number
					    && l.getSubject().equals(subject))
				.toArray(Lesson[]::new);

            helper.atMost(
		"One teacher teaches to maximum 1 group at a given time.", 1,
		    groups);

	}
    }
}

Програмиране на ограниченията(2)

Lesson[] lessons = lessonCombinations
	    	        .stream()
			.filter(l -> 
                            (l.getNumber() < 4 || l.getDay().equals(Day.Mon))
			    && l.getSubject().equals(Subject.Physics))
			.toArray(Lesson[]::new);

for (Lesson lesson : lessons) {
    helper.setFalse(lesson,
        "Physics teacher doesn't have morning classes
         and doesn't have classes on Monday.");
}

Резултати

Бъдещо развитие

• обработка на входни данни от потребителя
• изобразяване на графиците в по-удобен формат
• включване на кабинети/стаи в променливите
• задаване на приоритети на препоръчителните ограничения
• повече видове ограничения
• графичен потребителски интерфейс

Благодаря за вниманието!

Въпроси?