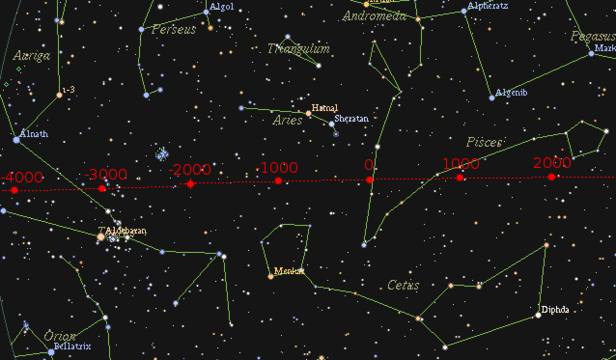
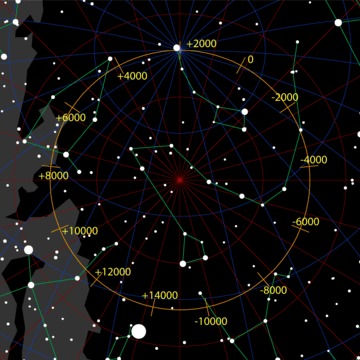
歲差
物理在地球科學上的應用
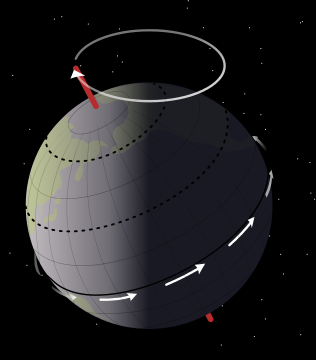
進動
\tau = \frac{dL}{dt}\\
\omega_p = \frac{\tau}{I_s\omega_s\sin{\theta}} =
\frac{\lvert \vec r \times \vec F \rvert }{I_s\omega_s\sin{\theta}}
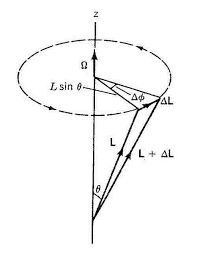
\Delta L = L \sin \theta \Delta \phi = \lvert \vec r \times \vec F \rvert \Delta t
潮汐力
重力加速度
\vec a_g = -\hat r G \frac{M}{(R\pm\Delta r)^2}\\
= -\hat r G \frac{M}{R^2} \frac{1}{(1\pm\frac{\Delta r}{R})^2}
\frac{1}{(1\pm x)^2} = 1 \mp 2x + 3x^2 \mp ...
泰勒展開式
\vec{a}_g = - \hat{r} ~ G ~ \frac{M}{R^2} \pm \hat{r} ~ G ~ \frac{2 M }{R^2} ~ \frac{\Delta r}{R} + \cdots
\vec{a}_{t,\text{axial}} \approx \pm \hat{r} ~ 2 \Delta r ~ G ~ \frac{M}{R^3}
潮汐加速度
\overrightarrow{T} = \frac{3Gm}{r^3}(C-A)\sin\delta\cos\delta\begin{pmatrix}\sin\alpha\\-\cos\alpha\\0\end{pmatrix}
潮汐力矩
Gm = 攝動天體的標準重力參數
r = 攝動天體到地心的距離
C = 圍繞地球自轉軸轉動的轉動慣量
A = 任何環繞地球赤道直徑的轉動慣量
C−A = 地球赤道隆起的轉動慣量(C>A)
δ = 攝動天體的赤緯 (赤道以南或北)
α = 攝動天體的赤經 (從春分點向東)
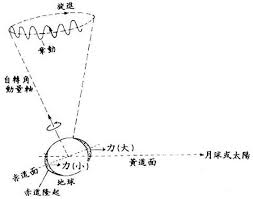
地軸進動
影響
週期約25,772年
受地球自轉速率、地月距離的變化影響
分點歲差
Title Text