數論

鐘奇恩

2022.4.26

〞

The Summit is what drives us, but the climb itself is what matters.

– Conrad Anker

自我介紹

ck1090943@gl.ck.tp.edu.tw

鐘奇恩

我弱故我在

特殊經歷

2018年和🉐及0+5A一起出國

歡迎大家來數學讀書會！

每週五18:00在夢紅樓4樓

FB社團：CK很強大之Team Work讀書會

加入社團遇到問題可以私訊我

什麼東西不是今天要講的

#include<iostream>
#include<string>
#include<vector>
#define int long long
using namespace std;
signed main(){
    int n0, n2, n;
    string a="", b="";
    cin >> n0 >> n2;
    n = n0+n2;
    if (n0==0 || n2==0) cout << -1 << endl;
    else if (n2%2==0){
        if (n0==1) {
            for (int i=0;i<n2-2;i++) a += "2";
            a += "022";
        }
        else {
            for (int i=0;i<n2-1;i++) a += "2";
            a += "002";
            for (int i=0;i<n0-2;i++) a += "0";
        }
        for (int i=0;i<n0-1;i++) b += "0";
        b += "220";
        for (int i=0;i<n2-2;i++) b += "2";
        cout << a << endl << b << endl;
    }
    else {
        if (n0<10 || n2<11 || (n2<13 && n0<11)) {
            cout << -1 << endl;
            return 0;
        }

        if (n0>=12){
            for (int i=0;i<n2-11;i++) a += "2";
            a += "20202020202020202020002";
            for (int i=0;i<n0-12;i++) a += "0";
        }
        else if (n0==11){
            for (int i=0;i<n2-11;i++) a += "2";
            a += "0202020202020202020202";
        }
        else {
            for (int i=0;i<n2-12;i++) a += "2";
            a += "0222020202020202020202";
        }

        if (n2>=13) {
            for (int i=0;i<n0-10;i++) b += "0";
            b += "2020202020202020202220";
            for (int i=0;i<n2-12;i++) b += "2";
        }
        else {
            for (int i=0;i<n0-11;i++) b += "0";
            b += "2020202020202020202020";
        }
        if (a.length()!=n || b.length()!=n) return -1;

        cout << a << endl << b << endl;
    }
    return 0;
}

課程大綱

小複習&小補充

Millar-Rabin

Pollard's rho

排容原理aka莫比烏斯反演
狄利克雷卷積

數論分塊

參考資料

小複習

小補充

同餘

定義

輾轉相除法

快速冪、模逆元

中國剩餘定理

質數

κόσκινον Ἐρατοσθένους

線性篩

質數密度估計

其他

歐拉函數phi

完全剩餘系

既約剩餘系

回想看看

常見迴圈

for(int i = 1; i <= n; i++)
	for(int j = 0; j <= n; j += i){
		do_something();    
}

•給還不熟歐拉函數的人:

1.為甚麼對任意互質的a,b，\phi(ab)=\phi(a)\phi(b)。

2.把\phi(d)對所有n的因數d sigma起來是\phi(n)。

•給還不熟費小的人:

1.為甚麼對所有質數p，a^p=a (mod p)。

2.給定質數p，證明有無限多個n使得p|(2^n+n)。

•給還不熟LTE的人:

1.對不整除x,y,n但整除x-y的質數p證明v_p(x^n-y^n)= v_p(x-y)。

2. p,q 為質數，若存在 a 使得 p | (a^q−1)/( a−1)，則 p = q 或 p |( q−1)。

•給想學習order的人:

1.給定互質的數a,m，令t為”最小的”正整數滿足a^t=1 (mod m)，為甚麼對任意的d滿足a^d=1 (mod m)都有d|m。

2.令 a,b 為互質的整數，n 為任意正整數，證明 a^{2^n} + b^{2^n} 的任意奇質因數皆為 2^{n+1}k + 1 的形式。

•給想學習原根的人:

1.令f(x)為次數為n的整係數多項式、p為質數。為什麼f(x)=0 (mod p)最多只有n個解。

2.為甚麼對任意p-1的因數d，皆存在order為d的人。

•給想學更多的人:

1.令k>2，為甚麼模2^k時，3的order總是2^{k-2}。

2.為甚麼{3^0,…,3^{2^{k-2}-1},-3^0,- 3^{2^{k-2}-1}}會構成模2^k的既約剩餘系。

 

5張志煥, Jeffrey Chang and 3 others

 

Our History

階與原根

純數學

我們都知道的歐拉定理

對所有互質的a,m有a^{\varphi (m)}\equiv 1 \pmod{m}\\
但滿足a^{d}\equiv 1 \pmod{m} 的最小d不一定是\varphi(m)！
最小的d稱作a模m的order(階)\\ 若d=\varphi(m)則稱a為模m的原根
模m存在原根\iff \\ m為2, 4, p^k, 2p^k

Millar-Rabin

a probabilistic primality test

Birthday-attack

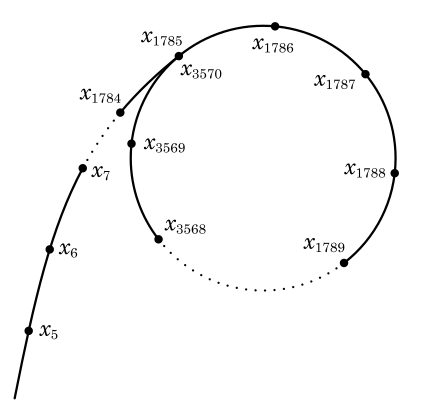
Pollard's rho

a probabilistic factorization

莫比烏斯反演

狄利克雷捲積

(f \ast g)(n) = \sum_

數論分塊

依\lfloor\frac{n}{i}\rfloor分塊

例子

\sum_{m=1}^n(n \mod m)

題目們

D - Index Trio (atcoder.jp)

簡單例題

Made with Slides.com