ННГУ им. Лобачевского 2022г.


Выполнил:

Хорькин Д.С. – 382006-3м

dmitryhorkin@gmail.com


Научный руководитель:

Смирнов Л. А. – доцент, к. ф-м н.

Кластерные вращательные режимы в системе глобально связанных фазовых осцилляторов с инерцией

Магистерская диссертация

"Национальный исследовательский Нижегородский государственный университет им. Н. И. Лобачевского"

Институт информационных технологий, математики и механики

Кафедра: Теории управления и динамики систем

Направление подготовки: "фундаментальная информатика и информационные технологии"

m\ddot{\varphi}_i + \dot{\varphi}_i = \omega + \frac{1}{N} \sum_{j = 1}^N \sin{(\varphi_j - \varphi_i - \alpha)},

где \(m\) - параметр инерции, \(\omega\) - постоянный вращающий момент, \(\alpha\) - фазовая задержка, \(N\) - общее число элементов

Введение и МОДЕЛЬ

[1] Sarkar M., Gupta S. Synchronization in the Kuramoto model in presence of stochastic resetting //arXiv preprint arXiv:2203.00339. – 2022.

[2] Sarkar M. Synchronization transition in the two-dimensional Kuramoto model with dichotomous noise //Chaos: An Interdisciplinary Journal of Nonlinear Science. – 2021. – Т. 31. – №. 8. – С. 083102.

[3] Solovev A., Friedrich B. M. Synchronization in cilia carpets and the Kuramoto model with local coupling: Breakup of global synchronization in the presence of noise //Chaos: An Interdisciplinary Journal of Nonlinear Science. – 2022. – Т. 32. – №. 1. – С. 013124.

[4] Wiesenfeld K., Colet P., Strogatz S. H. Synchronization transitions in a disordered Josephson series array //Physical review letters. – 1996. – Т. 76. – №. 3. – С. 404.

Модель Курамото описывает поведения большого набора связанных осцилляторов. Она мотивирована поведением реальных систем и  нашла широкое применение в биологии, нейронауке и физике.

m\ddot{\varphi}_i + \dot{\varphi}_i = \omega + \frac{1}{N} \sum_{j = 1}^N \sin{(\varphi_j - \varphi_i - \alpha)},

где \(m\) - параметр инерции, \(\omega\) - постоянный вращающий момент, \(\alpha\) - фазовая задержка, \(N\) - общее число элементов

Уединенные состояния

[5] Munyaev V.O., Bolotov M.I., Smirnov L.A., Osipov G.V., Belykh I. Stability of rotatory solitary states in Kuramoto networks with inertia // Physical Review E. V. 105. 2022. P. 024203. 18 February 2022

\(N - 1\)

\(1\)

m\ddot{\varphi}_i + \dot{\varphi}_i = \omega + \frac{1}{N} \sum_{j = 1}^N \sin{(\varphi_j - \varphi_i - \alpha)}

Цель работы

Целью данной работы является определение характеристик двухкластерных вращательных режимов в системе Курамото с инерцией  и связью Курамото-Сакагучи [6] для успешного достижения которой были поставлены следующие задачи:

  • Определение областей существования и типов возникающих двухкластерных вращательных режимов в зависимости от управляющих параметров
  • Определение устойчивости двухкластерных вращательных режимов в зависимости от управляющих параметров

  • Реализация программного комплекса, позволяющего эффективно находить интересующие вращательные движения, а также определять их устойчивость в произвольных системах связанных элементов

[6] H. Sakaguchi, Physical Review E 73, 031907 (2006).

где \(m\) - параметр инерции, \(\omega\) - постоянный вращающий момент, \(\alpha\) - фазовая задержка, \(N\) - общее число элементов

\begin{cases} m\ddot{\psi}_1 + \dot{\psi}_1 = \omega + \frac{N-K}{N} \sin{(\psi_2 - \psi_1 - \alpha)} - \frac{K}{N}\sin{\alpha},\\ m\ddot{\psi}_2 + \dot{\psi}_2 = \omega + \frac{K}{N} \sin{(\psi_1 - \psi_2 - \alpha)} - \frac{N - K}{N}\sin{\alpha}. \end{cases}
\begin{cases} m\ddot{\psi}_1 + \dot{\psi}_1 = \omega + (1 - \beta) \sin{(\psi_2 - \psi_1 - \alpha)} - \beta\sin{\alpha}, \\ m\ddot{\psi}_2 + \dot{\psi}_2 = \omega + \beta \sin{(\psi_1 - \psi_2 - \alpha)} - (1 - \beta)\sin{\alpha}. \end{cases}

Замена: \(\beta = \frac{K}{N}\)

двухкластерное состояние:

двухкластерный режим

\(N - K\)

\(K < N/2\)

X = \psi_1 - \psi_2, \\ m\ddot{X} + \dot{X} = (1 - 2 \beta) \sin{\alpha} - \left[(1-\beta)\sin{(X + \alpha)} + \beta\sin{(X - \alpha)} \right].
\frac{d^2 \Phi }{d\hat{t}^2} + \rho \frac{d\Phi}{d\hat{t}} + \sin{\Phi} = \gamma
R^2 = (N - 2K)^2 \sin{\alpha}^2 + N^2 \cos{\alpha}^2, \\ \rho = \sqrt{\frac{N}{m R}}, \ t = \hat{t} \frac{N}{\rho R}, \gamma = \frac{N - 2K}{R}\sin{\alpha}, \\ \Phi = X + \delta, \ \delta = \arccos{(\frac{N}{R}\cos{\alpha})}. \\

Замена переменных:

\begin{cases} m\ddot{\psi}_1 + \dot{\psi}_1 = \omega + (1 - \beta) \sin{(\psi_2 - \psi_1 - \alpha)} - \beta\sin{\alpha}, \\ m\ddot{\psi}_2 + \dot{\psi}_2 = \omega + \beta \sin{(\psi_1 - \psi_2 - \alpha)} - (1 - \beta)\sin{\alpha}. \end{cases}

Динамика Расстройки фаз

\(T(\rho)\) - кривая Трикомми

Click on equation (based on link)

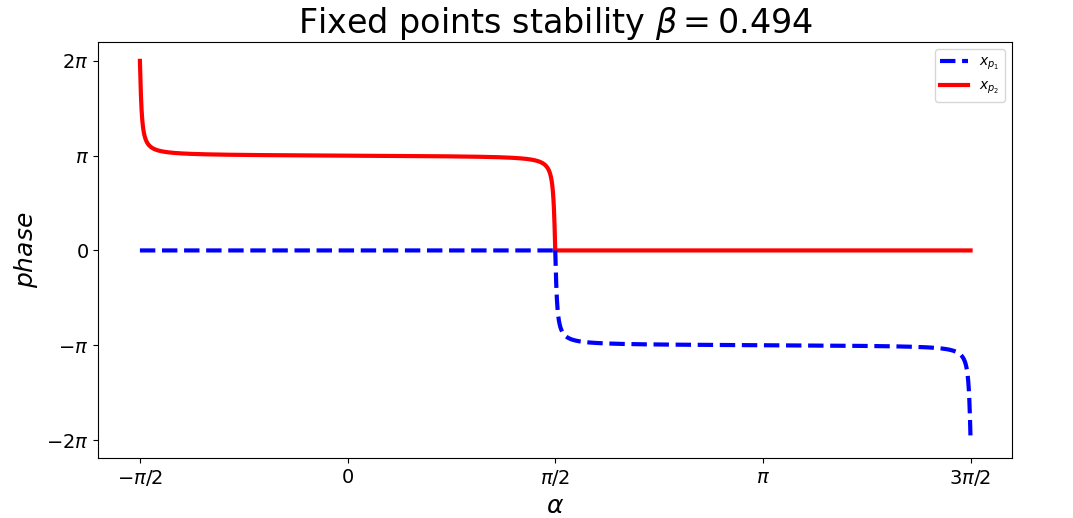
Анализ устойчивости стационарных состояний

При \(\beta \rightarrow  0.5\)  стационарные состояния равновесия стремятся к \(\pi\)

Потеря устойчивости в исходной системе

Тык :)

ВРАЩАЮЩАЯся расстройка фаз: СУЩЕСТВОВАНИЕ

Уравнение границ зон существования:

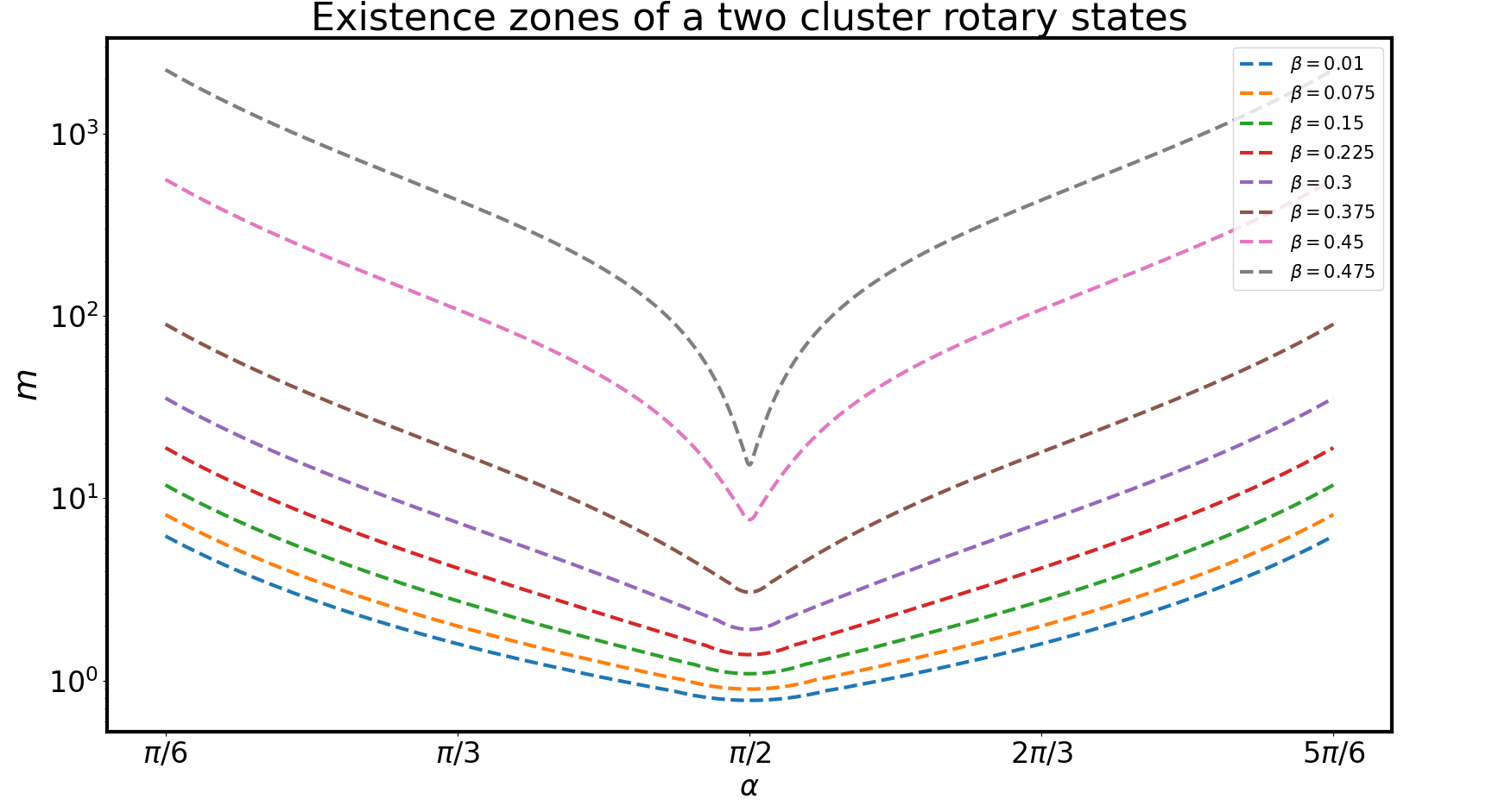
m = \frac{1}{\sqrt{(1 - 2\beta)^2\sin{\alpha}^2 + \cos{\alpha}^2} \cdot T_{ricommy}^{-1}(\frac{(1 - 2\beta)\sin{\alpha}}{\sqrt{(1 - 2\beta)^2\sin{\alpha}^2 + \cos{\alpha}^2}})}

Режим при \(\beta = 0.5\)  не существует. При фиксированном \(N\) cуществование режима при \(K=K^*\) также означает существование режимов \(K < K^*\)

двухкластерный режим

\begin{cases} m\ddot{\delta}_i + \dot{\delta}_i = \frac{1}{N} \left( \cos{\alpha} \sum_{j = 1}^K (\delta_j - \delta_i) + \cos{(X(t) + \alpha)} \sum_{j = K + 1}^N (\delta_j - \delta_i) \right), \ i = \overline{1,K}, \\ m\ddot{\delta}_i + \dot{\delta}_i = \frac{1}{N} \left( \cos{(X(t) - \alpha)} \sum_{j = 1}^K (\delta_j - \delta_i) + \cos{\alpha} \sum_{j = K + 1}^N (\delta_j - \delta_i) \right), \ i = \overline{K + 1,N}. \end{cases}
m\ddot{\delta}_i + \dot{\delta}_i = \frac{1}{N} \sum_{j = 1}^N \cos{(\psi_j - \psi_i - \alpha)} \cdot (\delta_j - \delta_i)
m\ddot{\varphi}_i + \dot{\varphi}_i = \omega + \frac{1}{N} \sum_{j = 1}^N \sin{(\varphi_j - \varphi_i - \alpha)}

линеаризация \(\varphi_i = \psi_i + \delta_i\)

\begin{cases} m\ddot{\psi}_1 + \dot{\psi}_1 = \omega + (1 - \beta) \sin{(\psi_2 - \psi_1 - \alpha)} - \beta\sin{\alpha}, \\ m\ddot{\psi}_2 + \dot{\psi}_2 = \omega + \beta \sin{(\psi_1 - \psi_2 - \alpha)} - (1 - \beta)\sin{\alpha}. \end{cases}

ВРАЩАЮЩАЯся РАССТРОЙКА ФАЗ: УСТОЙЧИВОСТЬ

\eta_1 = \frac{1}{K} \sum_{i = 1}^K \delta_i - \frac{1}{N - K} \sum_{i = K + 1}^N \delta_i, \\ \eta_2 = \frac{1}{K} \sum_{i = 1}^K \delta_i + \frac{1}{N - K} \sum_{i = K + 1}^N \delta_i, \\ \xi_n = \delta_{n+1} - \delta_n, \ 1 \leq n \leq K - 1, \\ \zeta_n = \delta_{n+1} - \delta_n, \ K + 1 \leq n \leq N - 1.

Мультипликаторы для \(\eta_{1,2}\):  1, 1, \(\exp{-\frac{T_x}{m}}\), \(\exp{-\frac{T_x}{m}}\)

\begin{cases} m\ddot{\eta}_1 + \dot{\eta}_1 + \left( \beta \cos{(X(t) - \alpha)} + (1 - \beta) \cos{(X(t) + \alpha)} \right) \eta_1 = 0, \\ m\ddot{\eta}_2 + \dot{\eta}_2 + \left( (1 - \beta) \cos{(X(t) + \alpha)} - \beta \cos{(X(t) - \alpha)} \right) \eta_1 = 0, \end{cases}
\begin{cases} m\ddot{\xi}_n + \dot{\xi}_n + \left( (1 - \beta) \cos{(X(t) + \alpha)} + \beta \cos{\alpha} \right) \xi_n = 0, \\ m\ddot{\zeta}_n + \dot{\zeta}_n + \left( (1 - \beta) \cos{\alpha} + \beta \cos{(X(t) - \alpha)} \right) \zeta_n = 0. \end{cases}

Замена координат:

ВРАЩАЮЩАЯся РАССТРОЙКА ФАЗ: УСТОЙЧИВОСТЬ

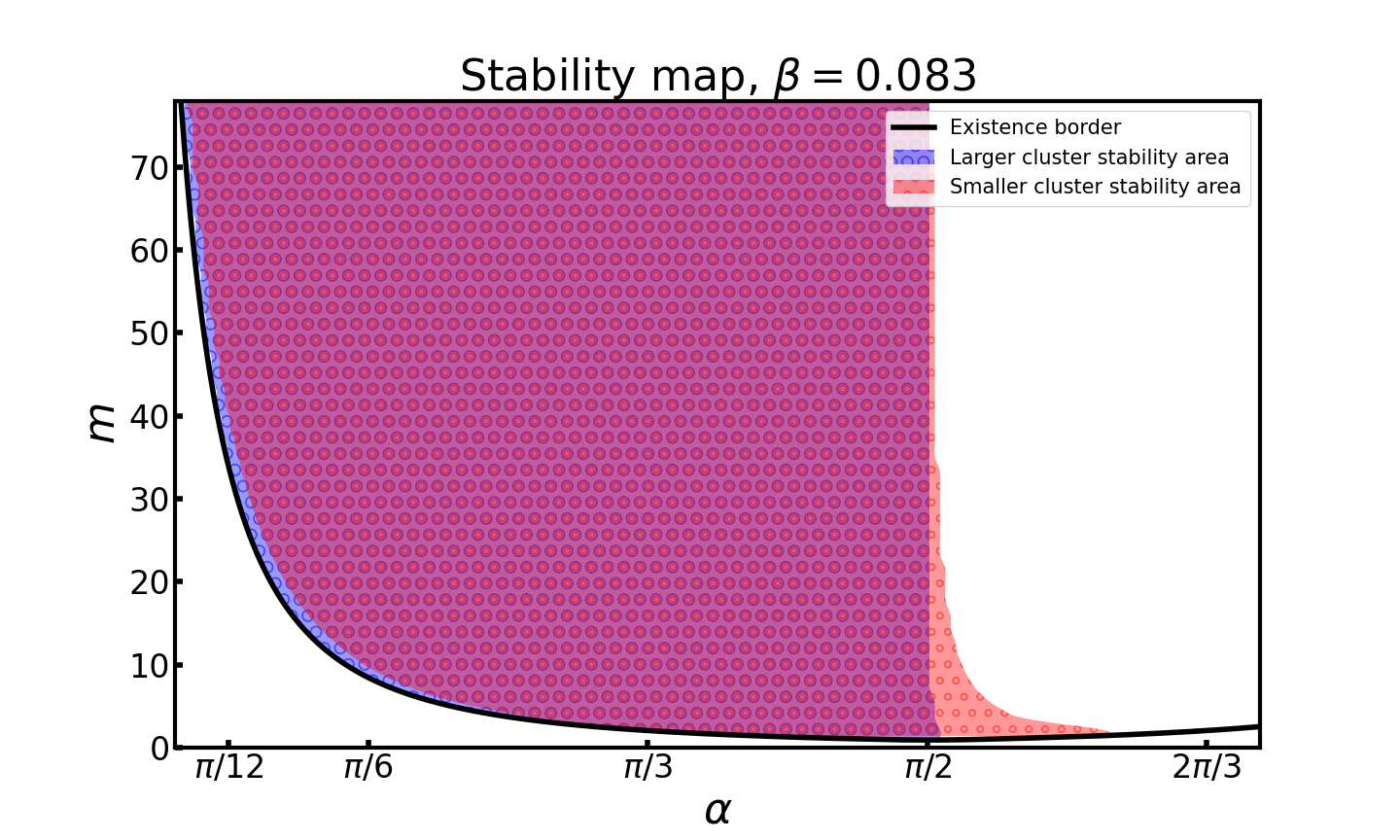
Карты устойчивости

Двухкластерный режим теряет устойчивость из-за потери устойчивости у одного из кластеров: как большего, так и меньшего

Карты устойчивости

Карты устойчивости

Область параметрической неустойчивости большого кластера. Развитие устойчивости в области отталкивающей связи

Карты устойчивости

Карты устойчивости

Развитие параметрической неустойчивости

Карты устойчивости

Разделение зоны устойчивости большого кластера на две несвязные компоненты. Развитие устойчивости в области отталкивающей связи

Карты устойчивости

пространственно временные диаграммы

пространственно временные диаграммы

пространственно временные диаграммы

пространственно временные диаграммы

пространственно временные диаграммы

ROTARY-STATES FRAMEWORK:

[7] Munyaev V. O. Khorkin, D., et al. Synchronization structures in the chain of rotating pendulums //Nonlinear Dynamics. – 2021. – Т. 104. – №. 3. – С. 2117-2125

[8] Munyaev V. O.  Khorkin D.,   et al. Appearance of chaos and hyperchaos in evolving pendulum network //Chaos: An Interdisciplinary Journal of Nonlinear Science. – 2021. – Т. 31. – №. 6. – С. 063106

[9] Khorkin, D., Bolotov, M., Smirnov, L. et al. Phase Control for the Dynamics of Connected Rotators. Autom Remote Control 81, 1499–1506 (2020)

Особенности:

  • just in time compilation (numba)
  • история разработки на github
  • тесты, настроенный CI
  • выложено в pypi

Предыдущие работы, использующие функциональность данного программного комплекса:

Спасибо за внимание

  • получено уравнение, описывающее границы областей существования интересующего вращательного движения
  • показано, что в системе существует два типа двухкластерных вращательных движений. Первый характеризуется постоянной расстройкой фаз, второй характеризуется вращающейся расстройкой фаз.
  • двухкластерное вращательное движение с постоянной расстройкой фаз является неустойчивым при любых значениях управляющих параметров
  • получена система независимо описывающая устойчивость каждого кластера
  • построены карты устойчивости двухкластерного режима в области параметров \(m\), \(\alpha\) в зависимости от параметра \(\beta = \frac{K}{N}\)
  • показано, что устойчивость двухкластерного режима часто может теряться из-за потери устойчивости у одного из кластеров, как малого, так и большого
  • разработан программный комплекс, позволяющий эффективно находить интересующие вращательные режимы и определять их устойчивость.

результаты:

Made with Slides.com