18/09/2018

3rd IPM Workshop, D. Vilsmeier

Resolving Profile Distortion
for Electron-based IPMs
using Machine Learning

D. Vilsmeier (GSI)
M. Sapinski (GSI)
R. Singh (GSI)

3rd IPM Workshop
J-PARC (Tokai, Japan)

18/09/2018

3rd IPM Workshop, D. Vilsmeier

What is Machine Learning?

Field of study that gives computers the ability to learn without being explicitly programmed.

- Arthur Samuel (1959)

"Classical"

approach:

+

=

Input

Algorithm

Output

Machine

Learning:

+

=

Input

Algorithm

Output

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Machine Learning Toolbox

Supervised Learning:

  • Artificial Neural Networks
  • Decision Trees
  • Linear Regression
  • k-Nearest Neighbor
  • Support Vector Machines
  • Random Forest
  • ... and many more

Unsupervised Learning:

  • k-Means Clustering
  • Autoencoders
  • Principal comp. analysis

Reinforcement Learning:

  • Q-Learning
  • Deep Deterministic Policy Gradient

18/09/2018

3rd IPM Workshop, D. Vilsmeier

IPM Profile Distortion

+V
-V

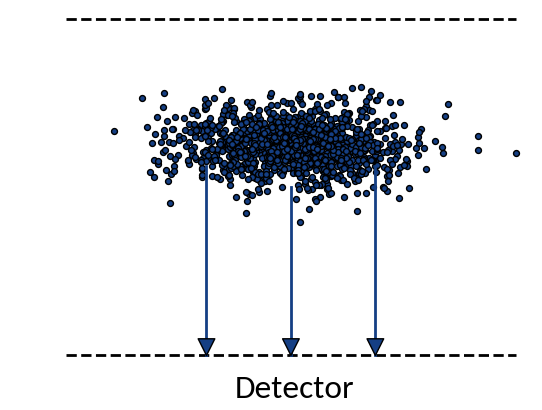
Ideal case

Particles move on straight lines towards the detector

Real case

Trajectories are influenced by initial momenta and by interaction with beam field

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Counteract via ...

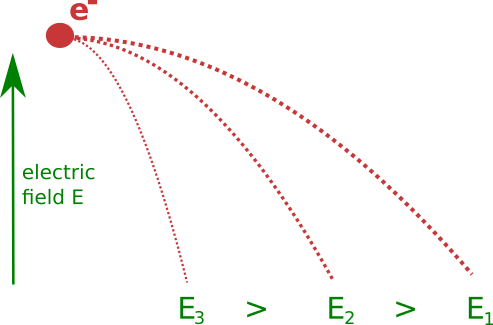
Increase of electric field

Resulting in smaller extraction times and hence smaller displacements; limit is quickly reached

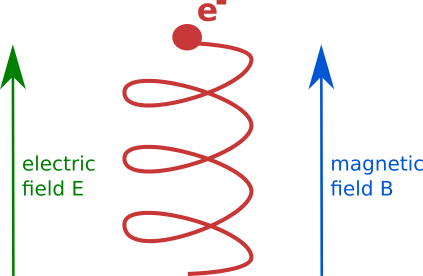
Additional magnetic field

Constrains the maximal displacement to the gyroradius of the resulting motion; usually an effective measure

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Distortion without magnetic field

  • Already observed in [W. DeLuca, IEEE 1969]
    (+ observation of focusing for electron collection)
  • R. E. Thern "Space-charge Distortion in the Brookhaven Ionization Profile Monitor" PAC 1987
    • Simulations + Measurements
    • Good agreement for nominal extraction voltages
    • Disagreement at lower extraction voltages
  • W. Graves "Measurement of Transverse Emittance in the Fermilab Booster" PhD 1994
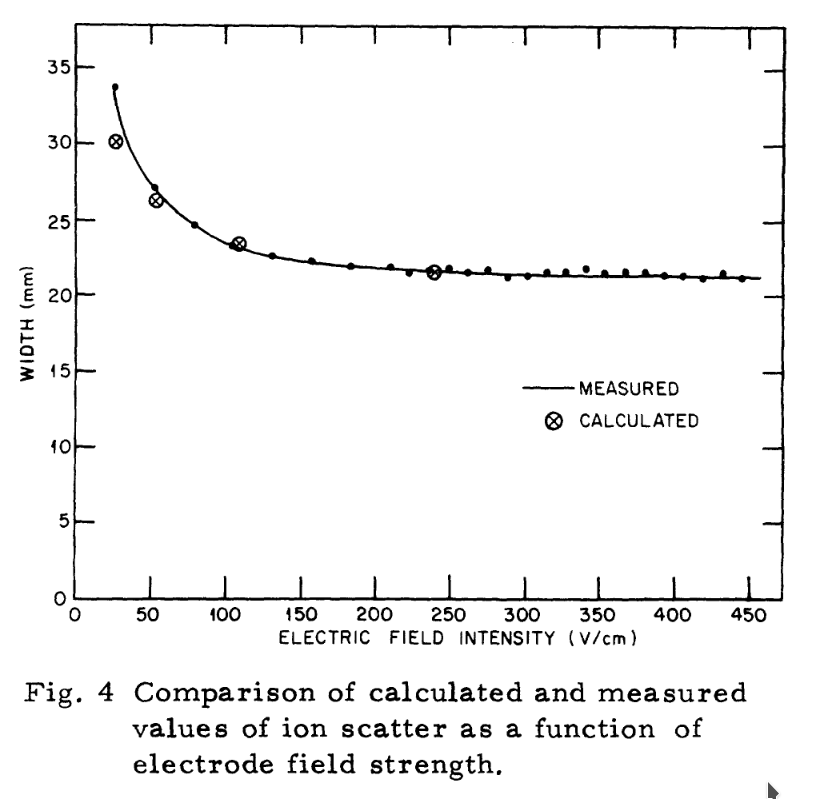
\sigma_{\textrm{beam}} = c_1 + c_2\sigma_{\textrm{measured}} + c_3N
\sigma_m = \sigma + 0.302\frac{N^{1.065}}{\sigma^{2.065}}\left(1 + 3.6\,R^{1.54}\right)^{-0.435}

+ other approaches, including non-Gaussian beam shapes via iterative procedures

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Distortion with magnetic field

  • More complex motion also due to the interaction with beam electric field
  • Capturing effects as well as different electromagnetic drifts play a role
  • Displacement from initial position can be mainly ascribed to three different effects:
    • Displacement of gyro-center due to initial velocities
    • Displacement of gyro-center due to space-charge interaction
    • Displacement due to gyro-motion above detector

Space-charge region

Detector region

(\Delta x_1)
(\Delta x_2)
(\Delta x_3)

🠖 Final motion is determined by effects in the "space-charge region"

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Electron trajectories

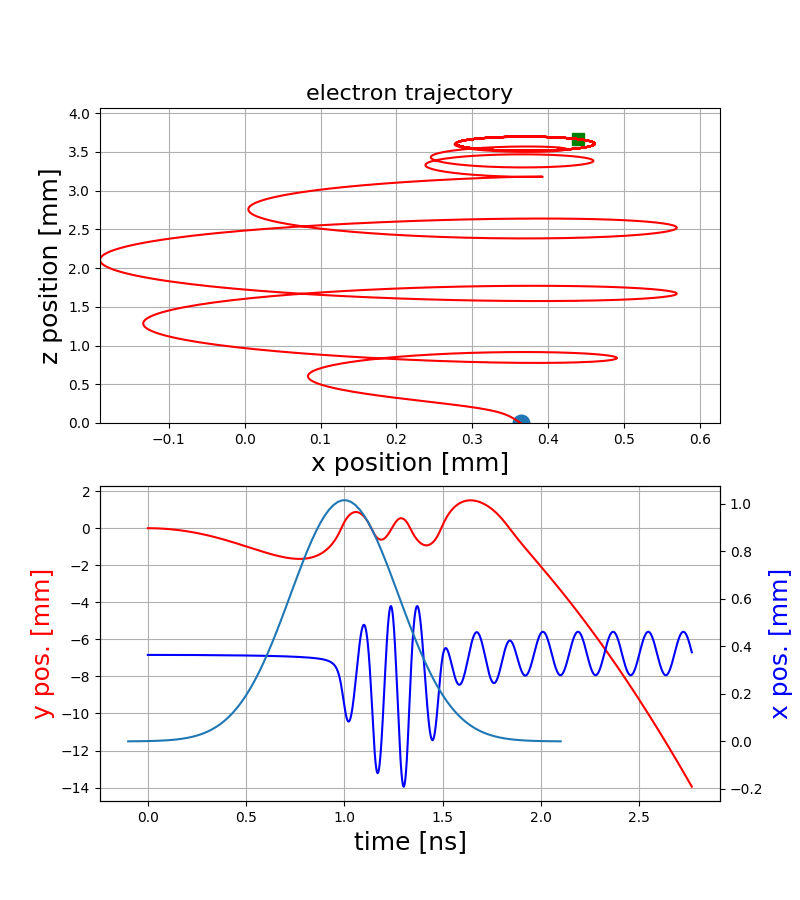
ExB-drift

Polarization drift

\left(\frac{d\vec{E}}{dt}\right)

Capturing

"Pure" gyro-motion

  • The resulting motion strongly depends on the starting position within the bunch and hence on the bunch shape itself
     
  • Various electromagnetic drifts / interactions create a complex dependence of the final gyro-motion on the initial conditions

p-bunch

Electron motion

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Gyro-radius increase

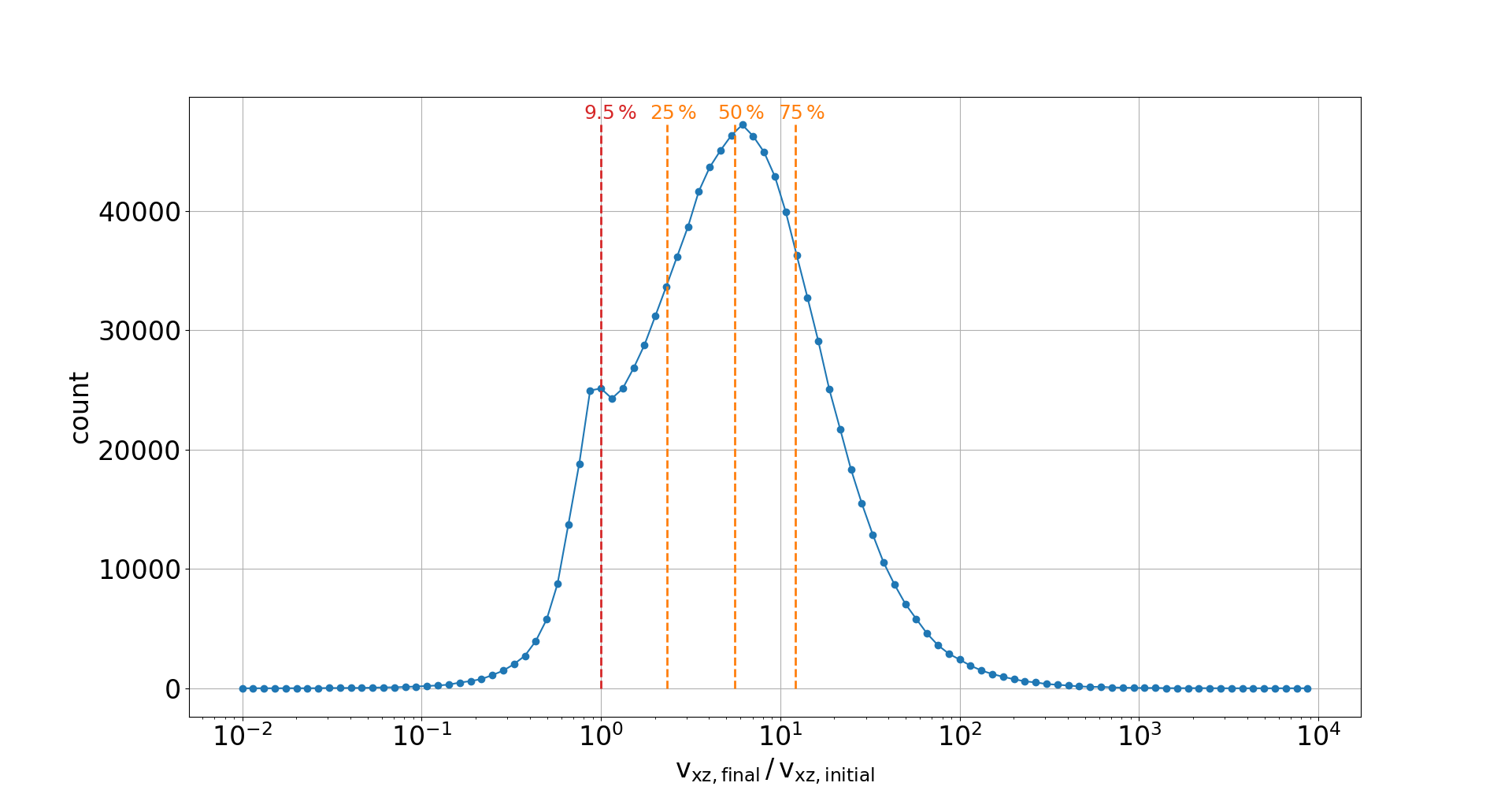
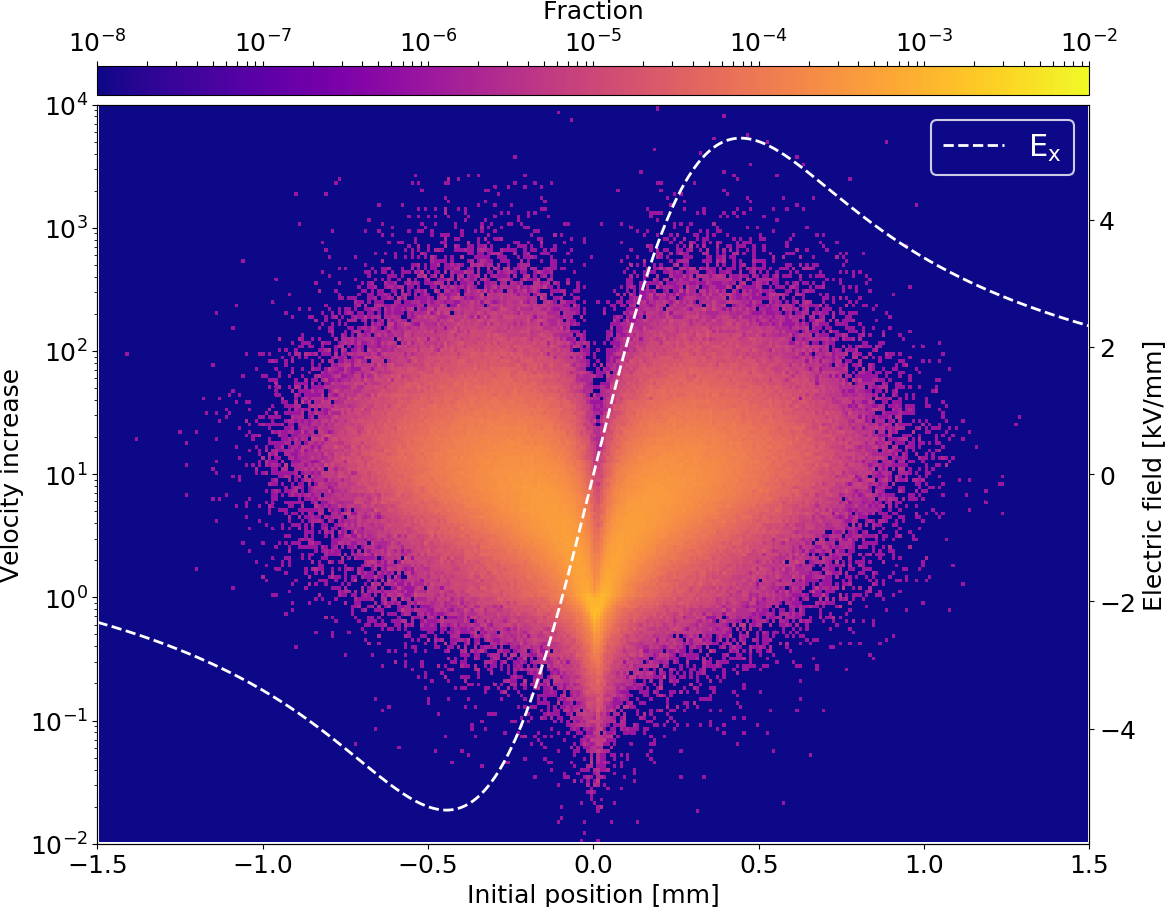
  • This interaction effectively results in an increase of gyro-radii which consequently determines the profile distortion

 

  • The increase itself depends on the starting position and thus on the bunch shape
    🠖 prevents usage of simple description by other beam parameters (e.g. point-spread functions)
     

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Profile distortion

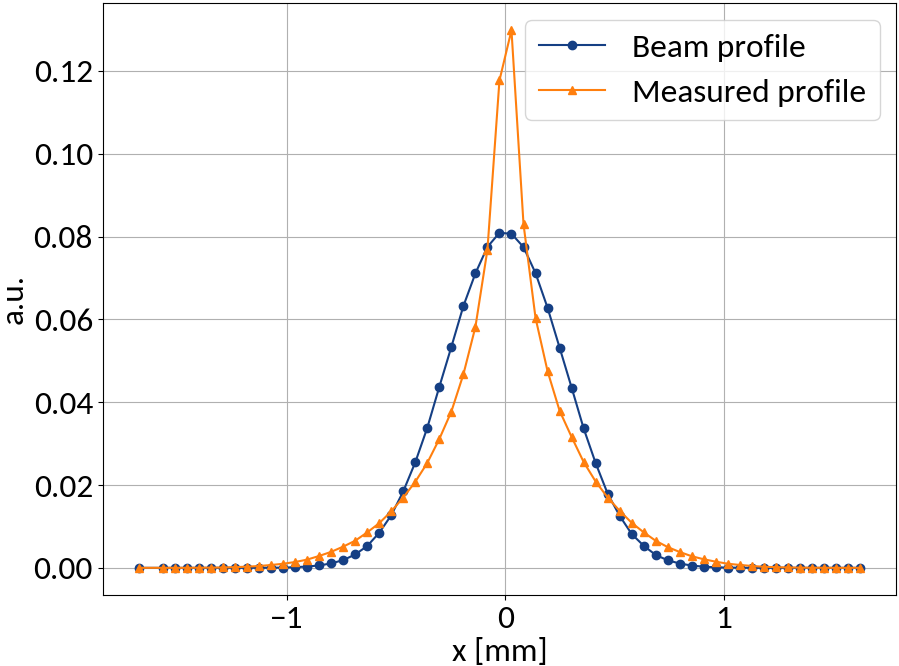
Ideally a one-dimensional projection the the transverse beam profile is measured, but...

\begin{aligned} & E \; & 6.5 \, \textrm{TeV} \\ & N_q \; & 2.1\cdot 10^{11} \\ & \sigma_x \; & 0.27 \, \textrm{mm} \\ & \sigma_y \; & 0.36 \, \textrm{mm} \\ & 4\sigma_z \; & 0.9 \, \textrm{ns} \end{aligned}

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Magnetic field increase

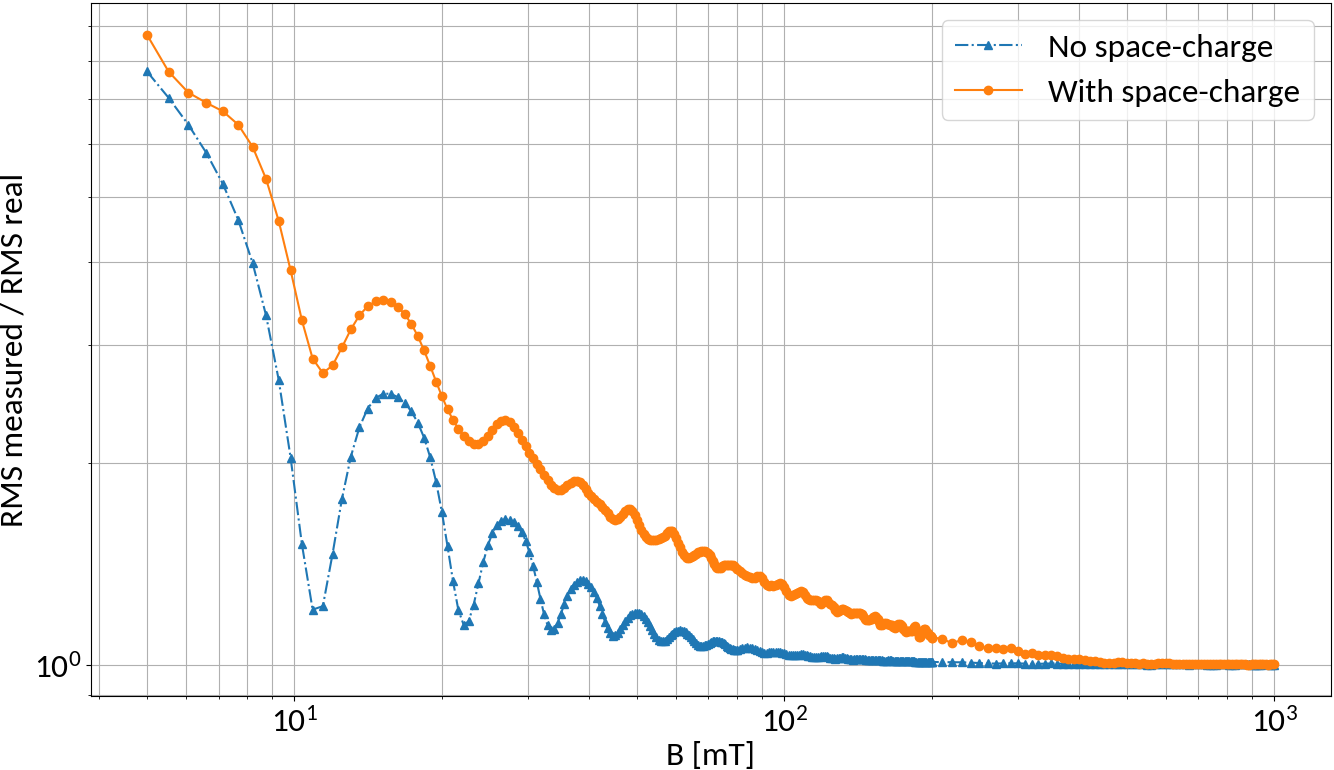
N-turn B-fields

Without space-charge electrons at the bunch center will perform exactly N turns for specific magnetic field strengths

Due to space-charge interaction only large field strengths are effective though

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Using Machine Learning

Parameter Range Step size
Bunch pop. [1e11] 1.1 -- 2.1 ppb 0.1 ppb
Bunch width (1σ) 270 -- 370 Ξm 5 Ξm
Bunch height (1σ) 360 -- 600 Ξm 20 Ξm
Bunch length (4σ) 0.9 -- 1.2 ns 0.05 ns

Protons

6.5 TeV

4kV / 85mm

0.2 T

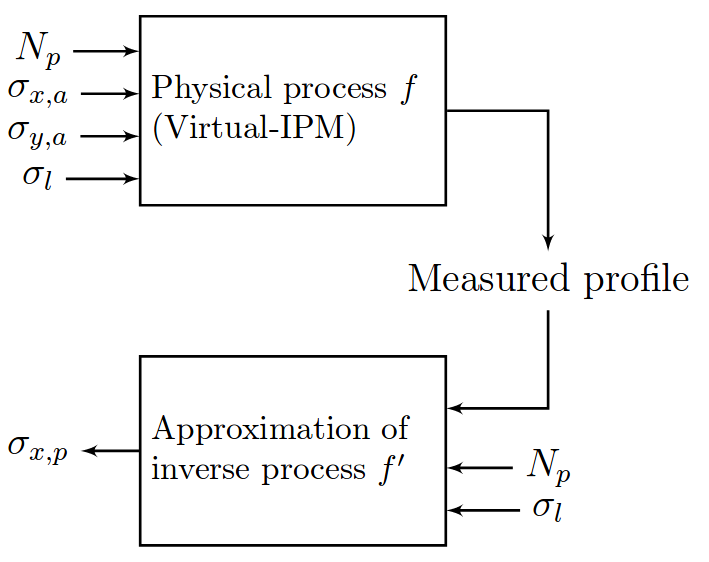
Training

Validation

Testing

Used to fit the model; split size ~ 60%.

Check generalization to unseen data; split size ~ 20%.

Evaluate final model performance; split size ~ 20%.

Consider 21,021 different cases

1

2

3

https://pypi.org/project/virtual-ipm

🠖 Evaluated on grid data and randomly sampled data

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Artificial Neural Networks

Input layer

Weights

Bias

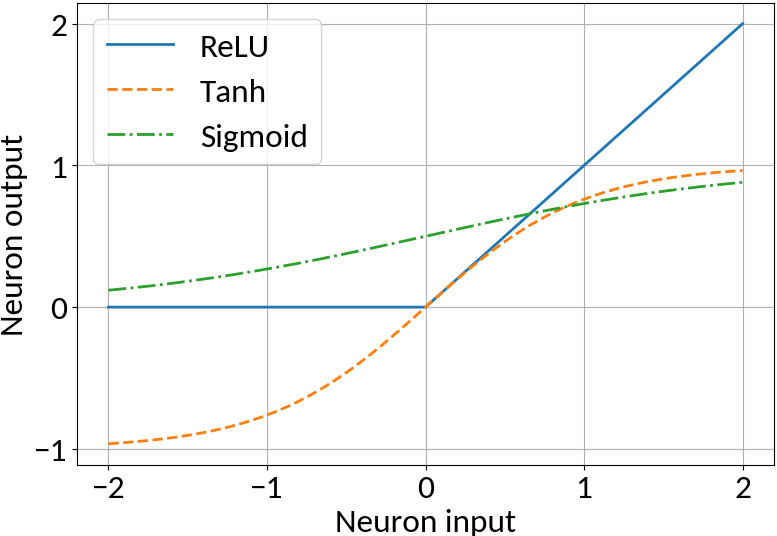
Apply non-linearity, e.g. ReLU, Tanh, Sigmoid

Perceptron

y(x) = \sigma\left( W\cdot x + b \right)

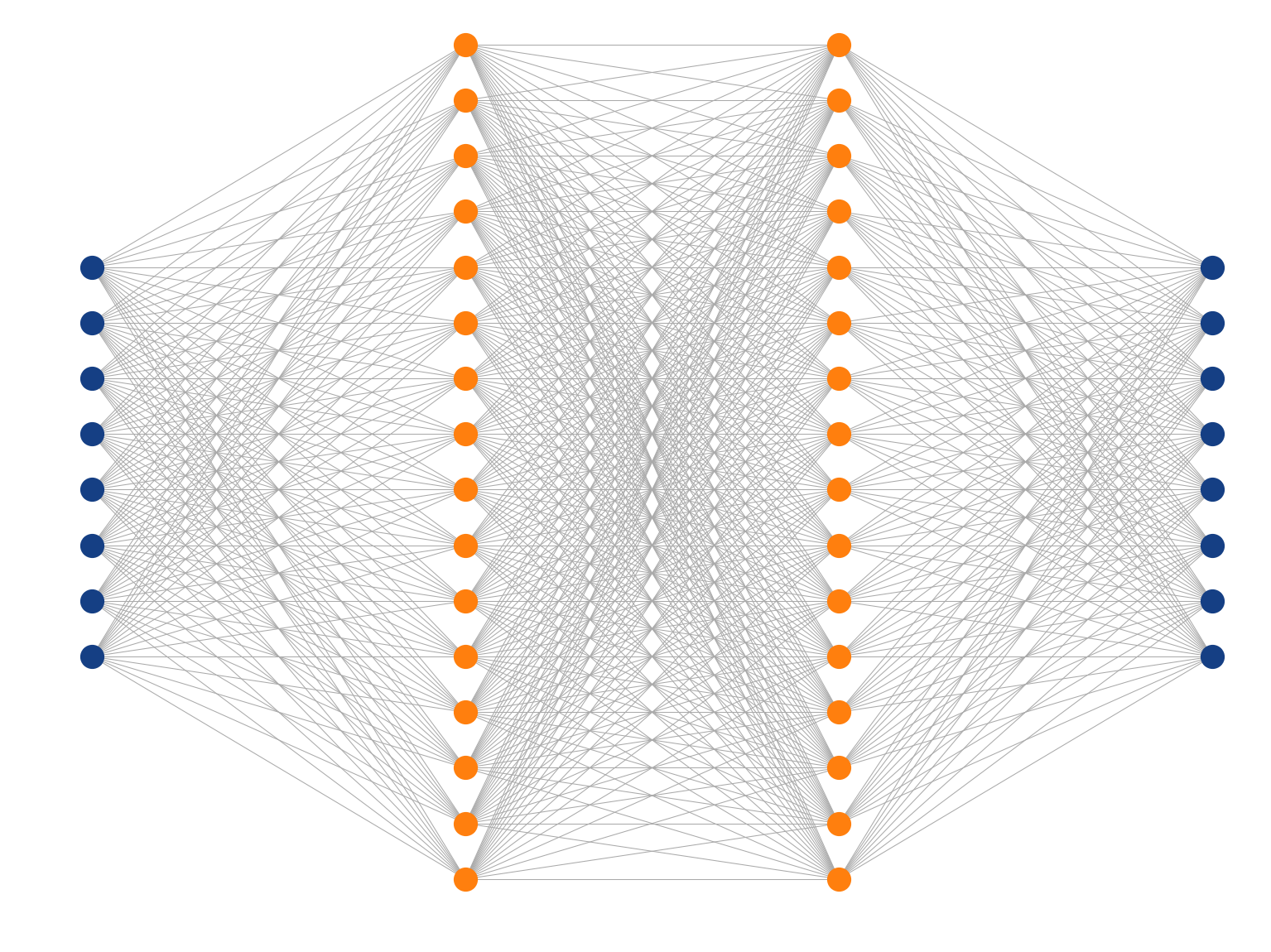
Multi-Layer Perceptron

Inspired by the human brain, many "neurons" linked together

Map non-linearities through non-linear activation functions

18/09/2018

3rd IPM Workshop, D. Vilsmeier

ANN Implementation 

IDense = partial(Dense, kernel_initializer=VarianceScaling())

# Create feed-forward network.
model = Sequential()

# Since this is the first hidden layer we also need to specify
# the shape of the input data (49 predictors).
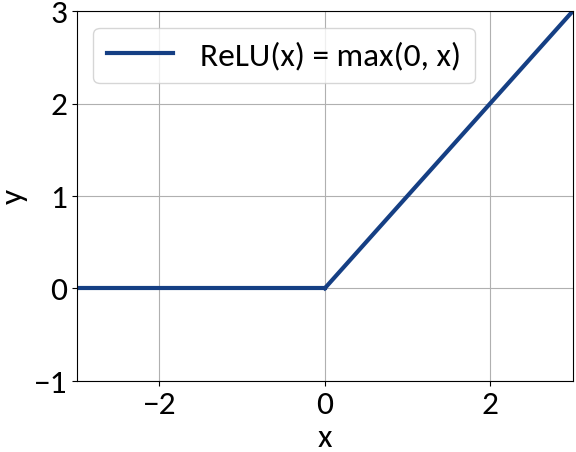
model.add(IDense(200, activation='relu', input_shape=(49,))
model.add(IDense(170, activation='relu'))
model.add(IDense(140, activation='relu'))
model.add(IDense(110, activation='relu'))

# The network's output (beam sigma). This uses linear activation.
model.add(IDense(1))
model.compile(
    optimizer=Adam(lr=0.001),
    loss='mean_squared_error'
)

model.fit(
    x_train, y_train,
    batch_size=8, epochs=100, shuffle=True,
    validation_data=(x_val, y_val)
)

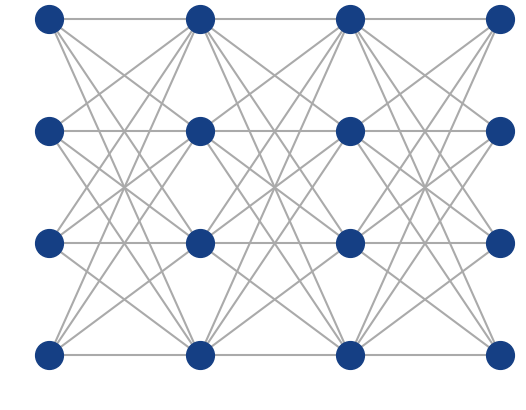
Fully-connected
feed-forward
network

with ReLU
activation
function

D. Kingma and J. Ba, "Adam: A Method for Stochastic Optimization", arXiv:1412.6980, 2014

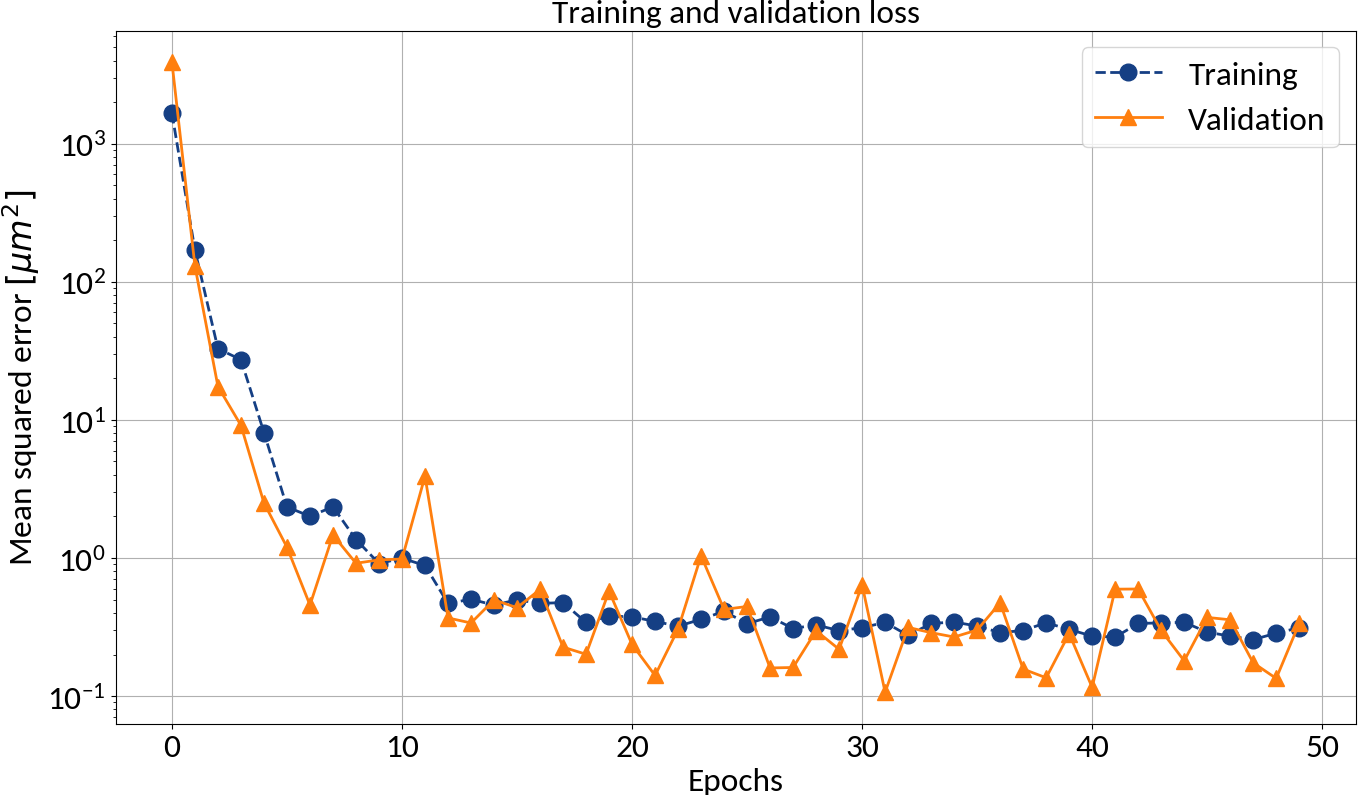
After each epoch compute loss on validation data in order to prevent "overfitting"

Batch learning
🠖 Iterate through training set multiple
times (= epochs)
🠖 Weight updates are performed in batches (of training samples)

keras

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Why ANNs?

Universal approximation theorem

Every finite continuous "target" function can be approximated with arbitrarily small error by feed-forward network with single hidden layer

[corresponding Cybenko 1989; Hornik 1991]

y = \sum_j^n w_j^o \cdot \sigma\left( \sum_k^d w_{jk}^h x_k + b_j \right)

\(n\) hidden units

activation function

\(d\) - dimensional domain

parameters to be "optimized"

Proof of existence, i.e. no universal optimization algorithm exists 🠖 "No free lunch theorem"

Works on compact subsets of \(\mathbb{R}^d\)

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Profile RMS Inference - Results

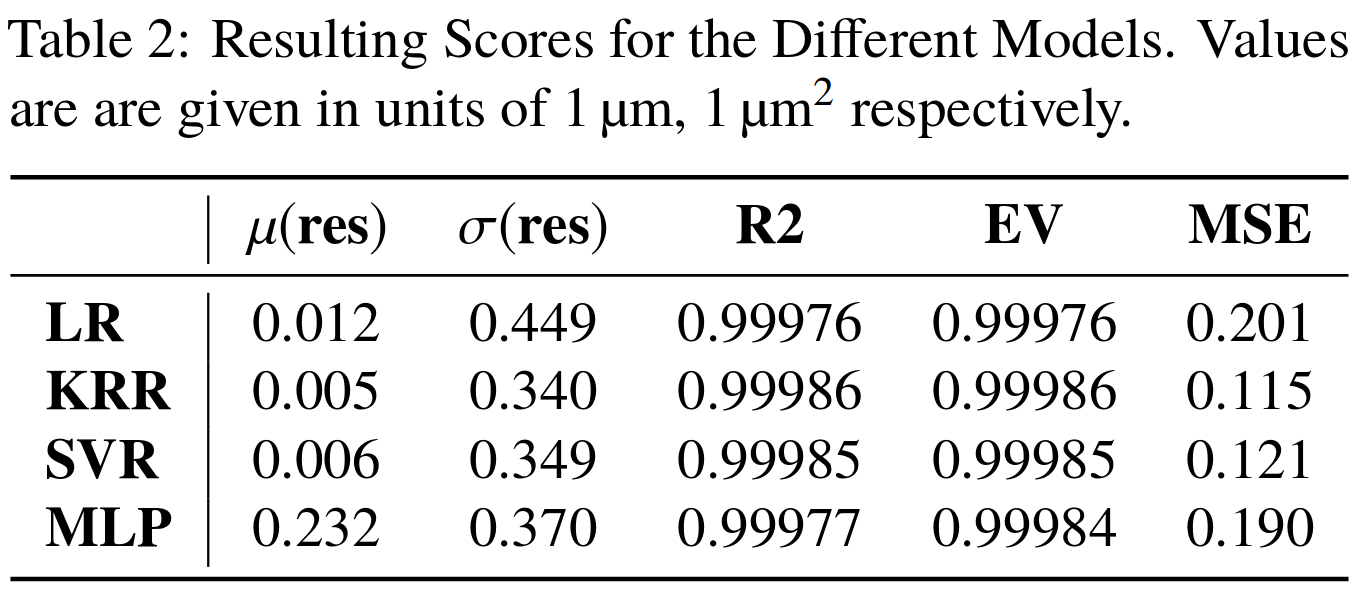
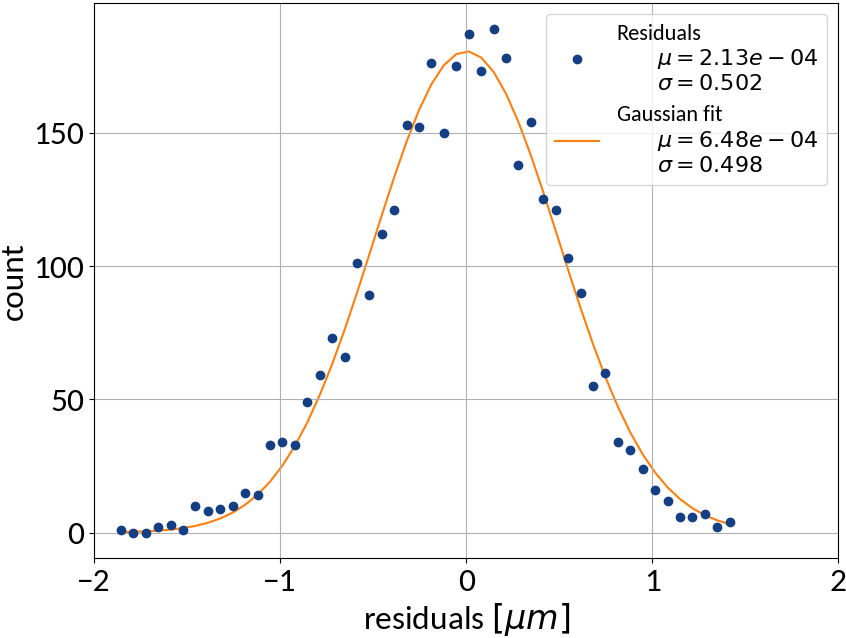
Tested also other machine learning algorithms:

â€Ē Linear regression (LR)
â€Ē Kernel ridge regression (KRR)
â€Ē Support vector machine (SVR)

Multi-layer perceptron (= ANN)

Very good results on simulation data 🠖 below 1% accuracy

Results are without consideration of noise on profile data

18/09/2018

3rd IPM Workshop, D. Vilsmeier

RMS Inference with Noise

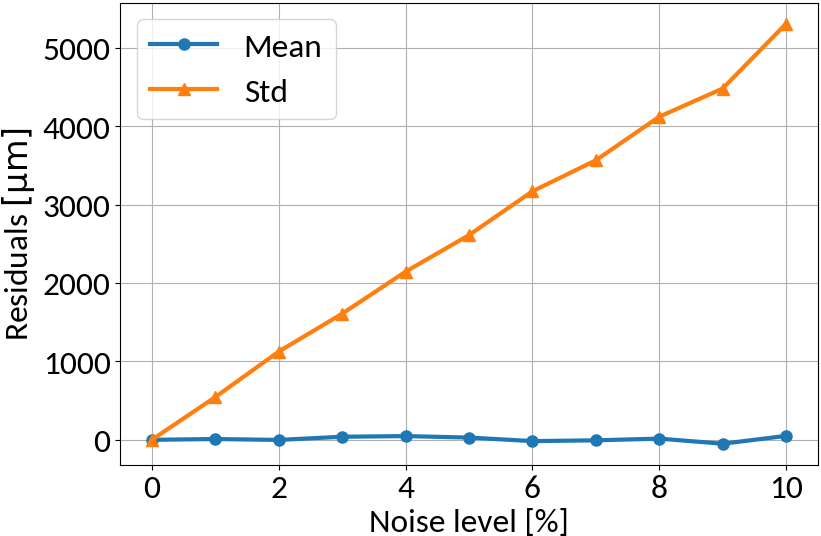
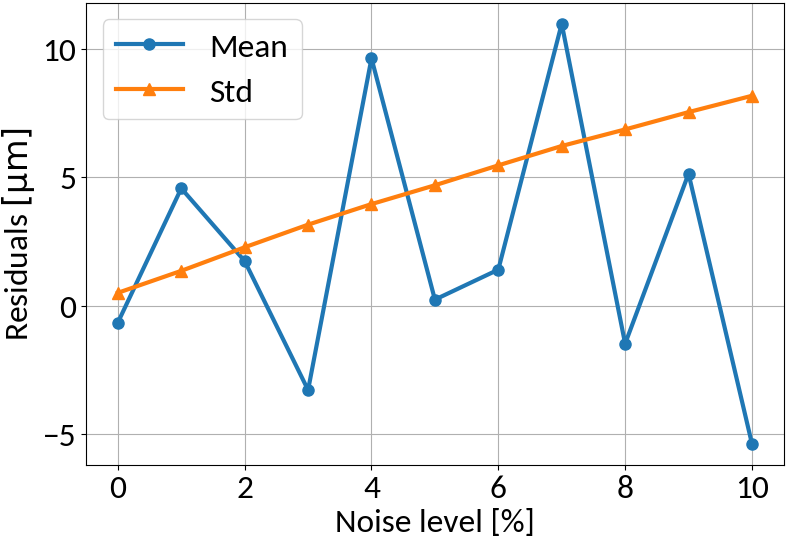
Linear regression model

no noise on training data

similar noise on training data

Linear regression amplifies noise in predictions if not explicitly trained

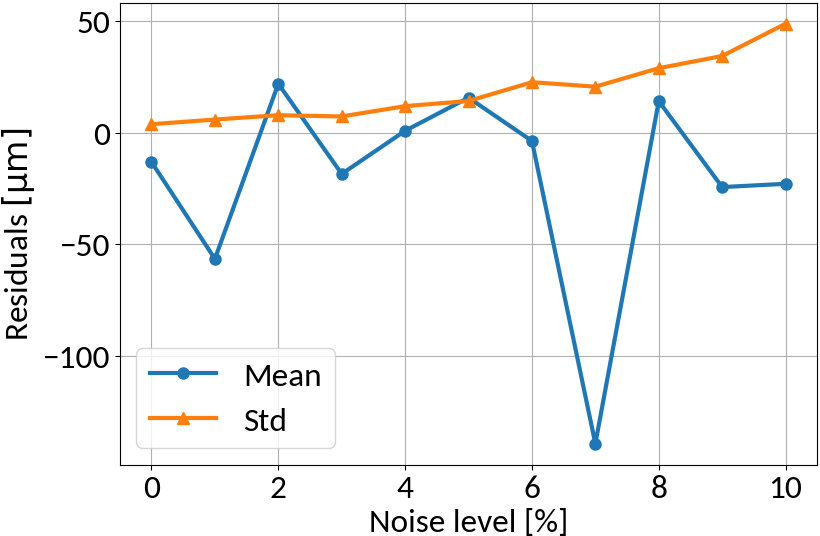
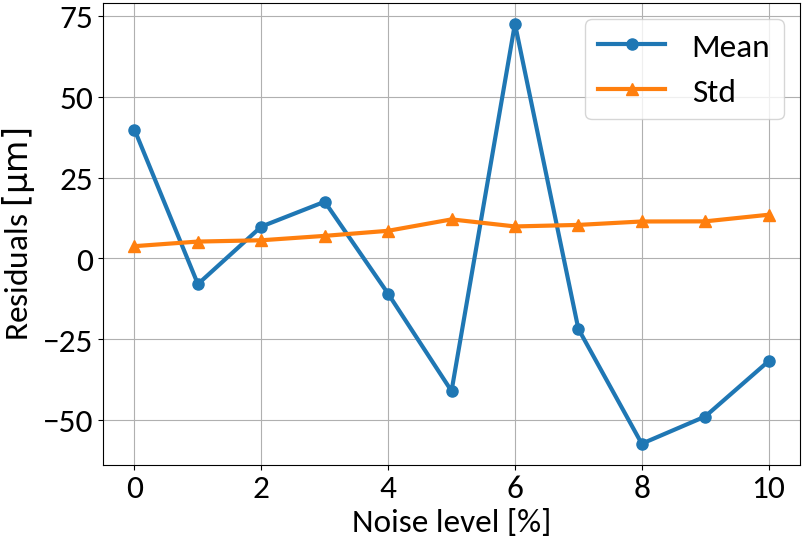
Multi-layer perceptron

MLP amplifies noise; bounded activation functions could help; as well as duplicating data before "noising"

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Full Profile Reconstruction

So far:

Machine Learning Model

\sigma_z
N
\sigma_x

Instead:

Machine Learning Model

\sigma_z
N

Compute beam RMS

Compute beam profile

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Gaussian bunch shape

MLP Architecture

  • 2 hidden layers, 88 nodes

  • tanh activation function

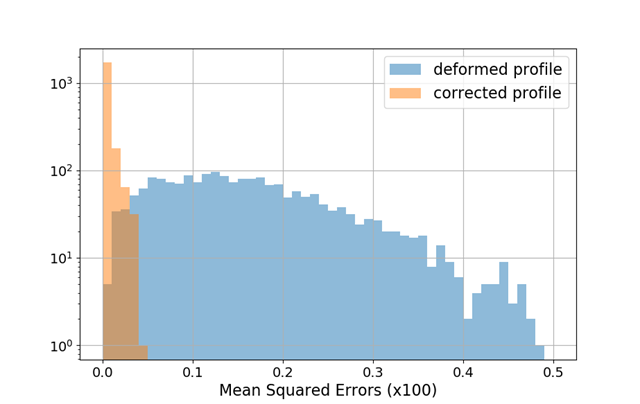
Performance measure

  • Mean squared error (MSE)
\textrm{MSE} = \frac{1}{N}\sum_{i=1}^{N}\left( y_{p,i} - y_{i} \right)^2

prediction

target

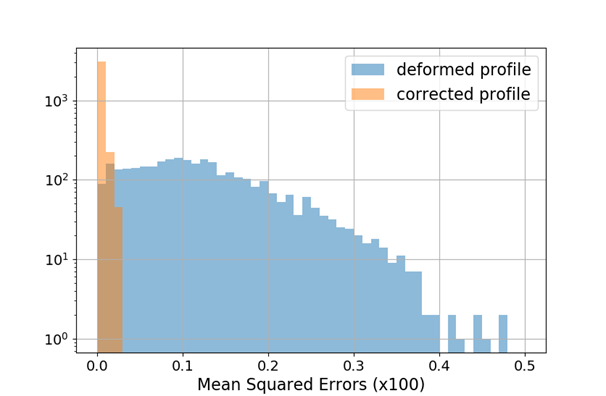
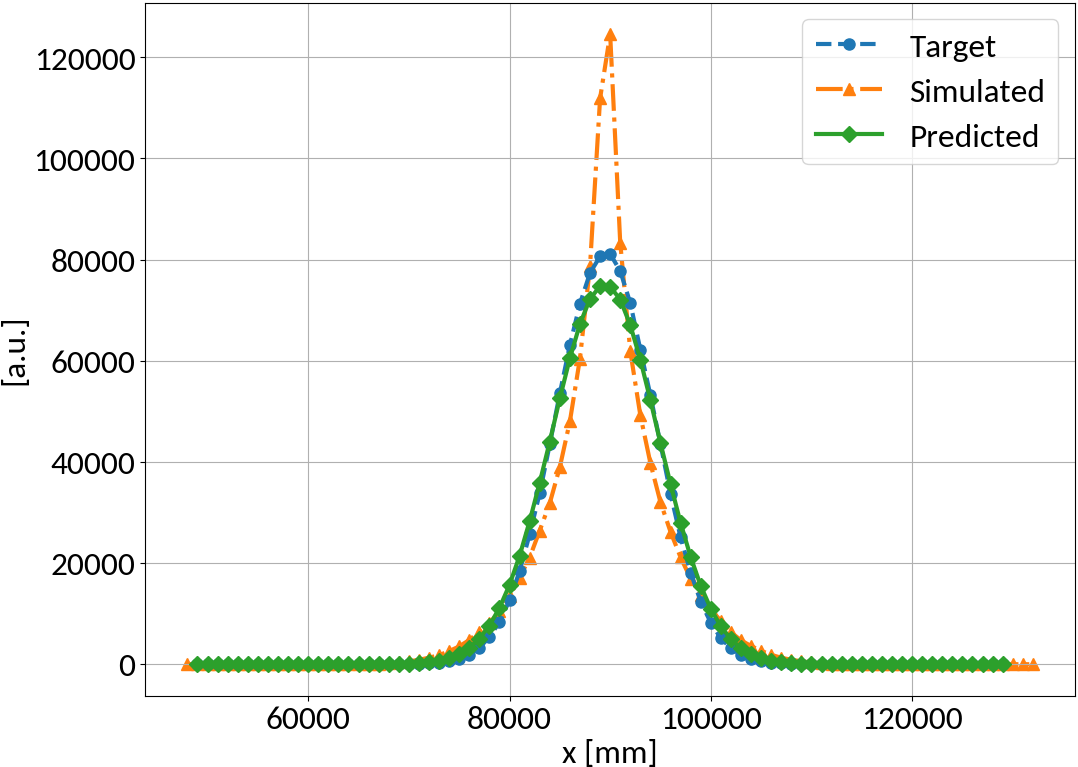
\begin{aligned} \textrm{mean} &= 0.1231 \\ \textrm{std} &= 0.0808 \end{aligned}
\begin{aligned} \textrm{mean} &= 0.0024 \\ \textrm{std} &= 0.0045 \end{aligned}

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Generalized Gaussian bunch shape

\frac{\beta}{2\alpha\Gamma(1/\beta)}e^{-\left(\lvert x-\mu\rvert/\alpha\right)^{\beta}}

Gen-Gauss used for testing while training (fitting) was performed with Gaussian bunch shape

\beta = 3
\beta = 1.5

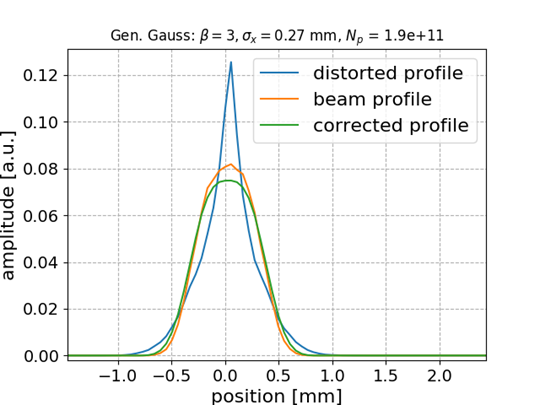
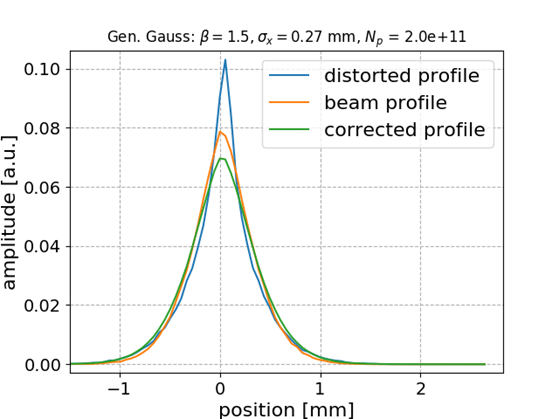
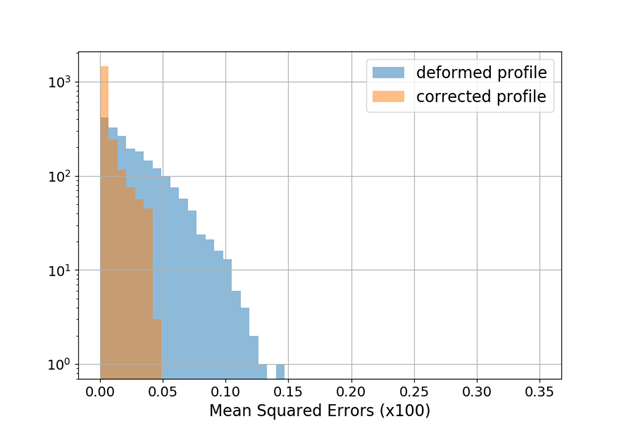
Smaller distortion in this case

\begin{aligned} \textrm{mean} &= 0.0278 \\ \textrm{std} &= 0.0237 \end{aligned}
\begin{aligned} \textrm{mean} &= 0.0068 \\ \textrm{std} &= 0.0087 \end{aligned}
\begin{aligned} \textrm{mean} &= 0.1638 \\ \textrm{std} &= 0.0974 \end{aligned}
\begin{aligned} \textrm{mean} &= 0.0051 \\ \textrm{std} &= 0.0064 \end{aligned}

ANN model generalizes to different beam shapes

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Q-Gaussian bunch shape

\frac{\sqrt{\beta}}{C_q}\left[1 - (1 - q)\beta x^2\right]^{\frac{1}{1-q}}

Q-Gauss used for testing while training (fitting) was performed with Gaussian bunch shape

q = 0.6
q = 2.0
\begin{aligned} \textrm{mean} &= 0.0013 \\ \textrm{std} &= 0.0003 \end{aligned}
\begin{aligned} \textrm{mean} &= 0.0042 \\ \textrm{std} &= 0.0038 \end{aligned}
\begin{aligned} \textrm{mean} &= 0.2034 \\ \textrm{std} &= 0.1034 \end{aligned}
\begin{aligned} \textrm{mean} &= 0.0057 \\ \textrm{std} &= 0.0068 \end{aligned}

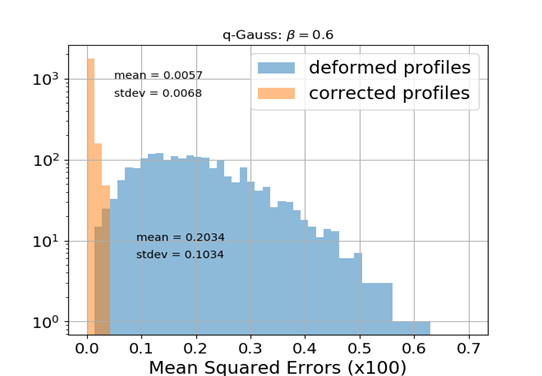
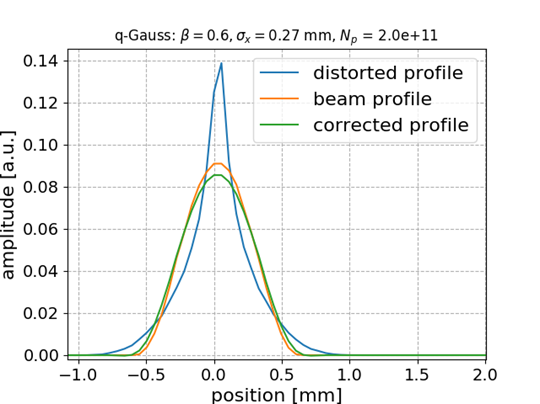
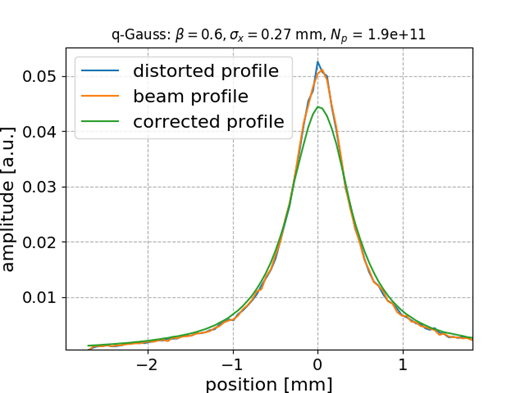
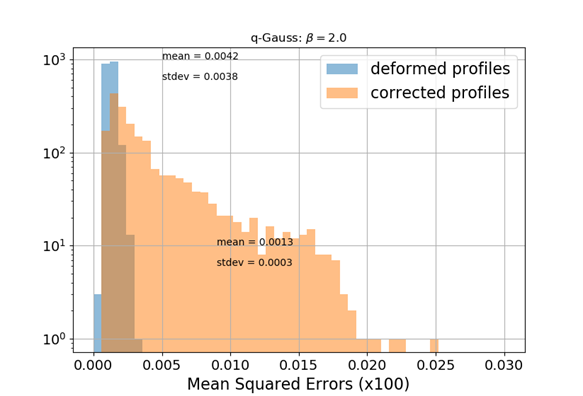
No distortion for this case
🠖 nothing to correct for; MLP preserves the state

ANN model generalizes to different beam shapes

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Model prediction uncertainty

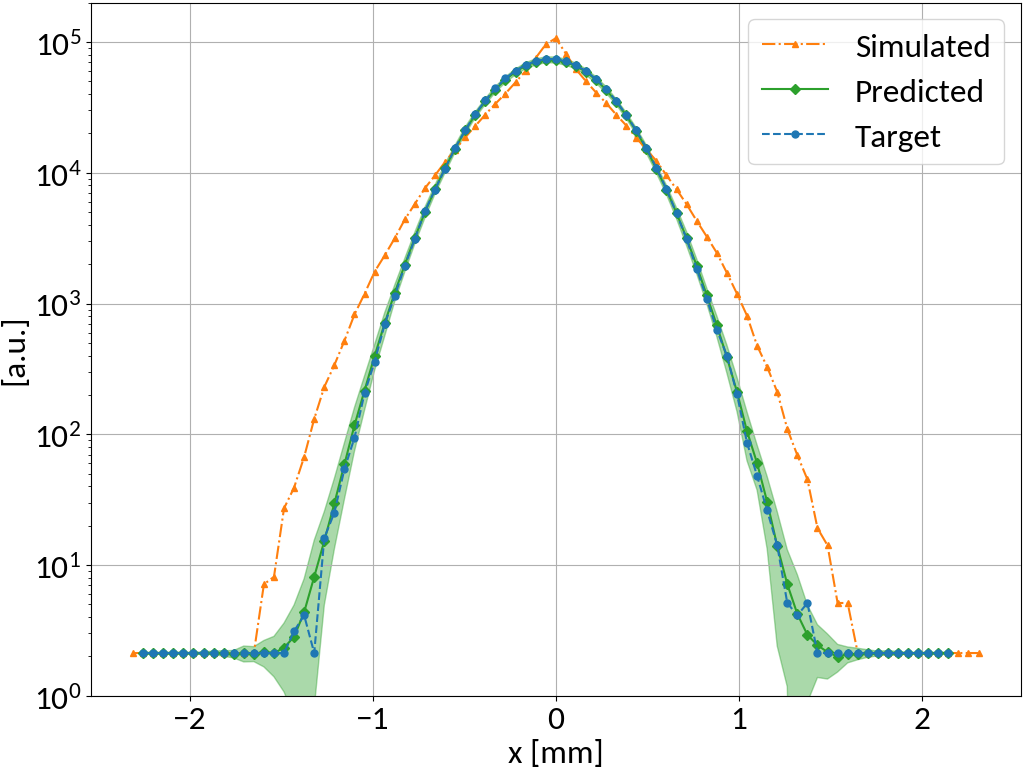
  • Could train multiple models with different initialization and different data presentation 🠖 ensemble of predictions
  • Emulate multi-model ensemble by using "Dropout" layers (also for predictions)

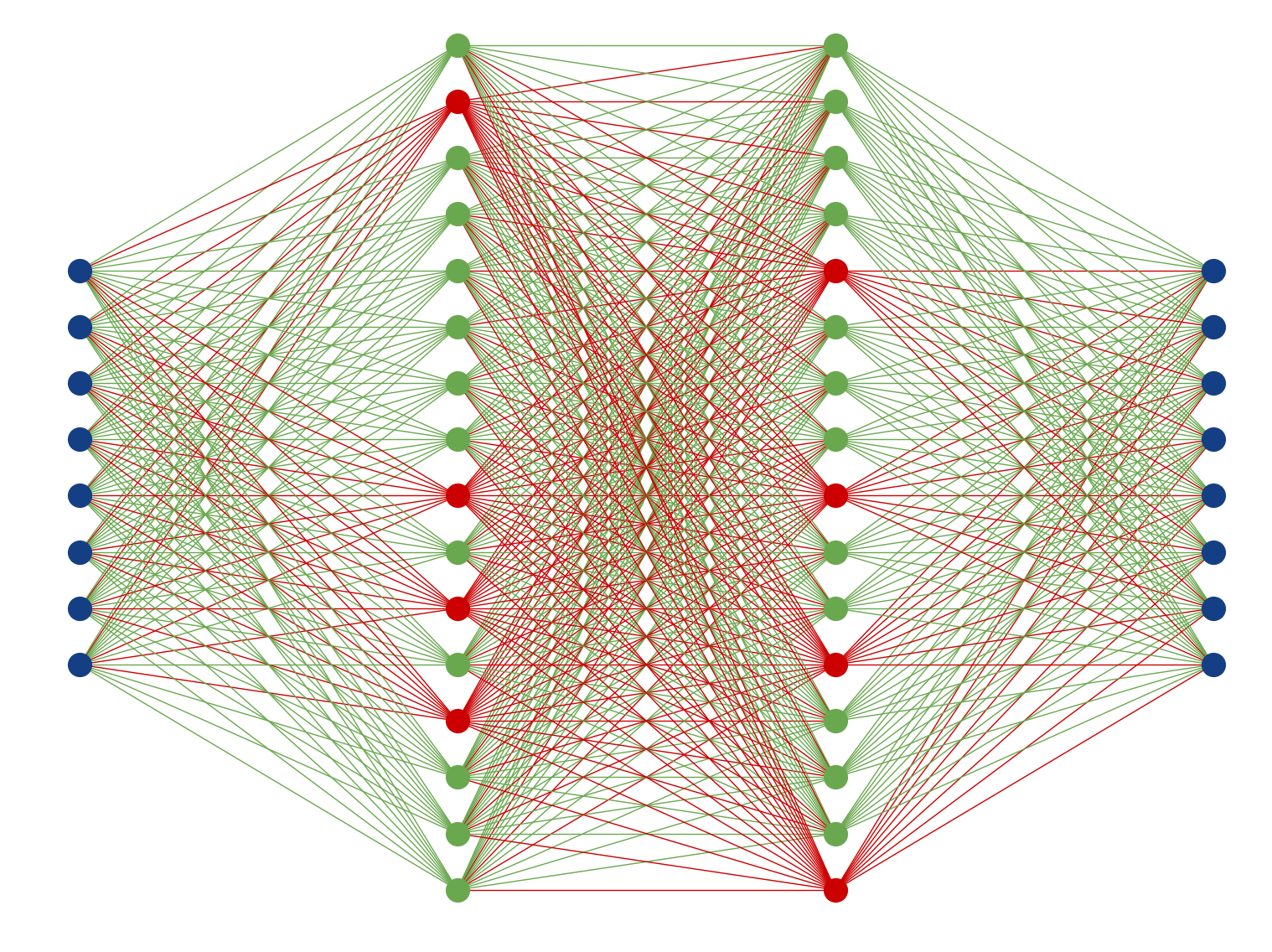
inactive

active

MLP shows very small standard deviation in predictions 🠖 the fitting converged well, small model uncertainty

\pm 1\sigma

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Sub-resolution measurements

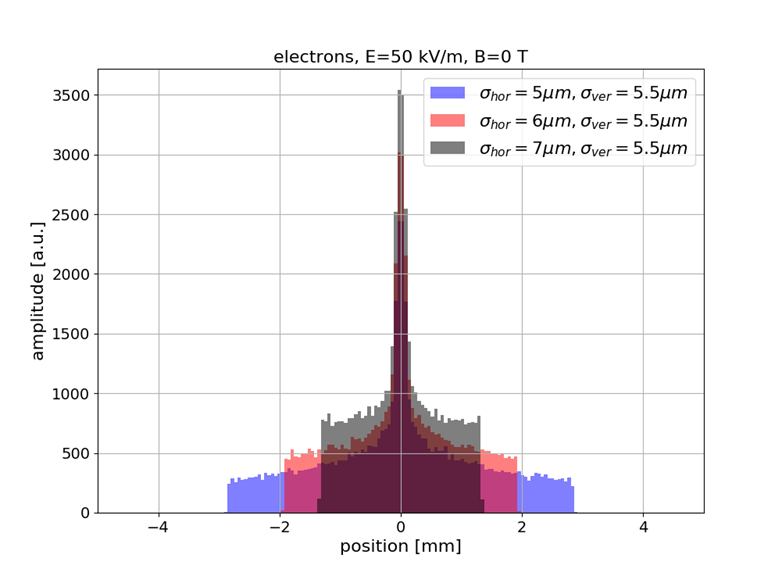
  • Understanding or (machine) "learning" beam profile deformation (and how to revert it), this information could be used to measure beams that are smaller than the resolution of the detector (by provoking a deformation / blow-up, then reverting it)
  • Example: SwissXFEL, 5.8 GeV electrons, 230 pC bunch charge, 21 fs bunch length, 5-7 Ξm transverse size
  • Bunch size is 1/10-th of detector resolution however the deformed profile is well above and strongly depends on the bunch size
  • Alternative to R. Tarkeshian et al. Phys. Rev. X 8, 021039 (reconstruction based on ion energies)

preliminary

18/09/2018

3rd IPM Workshop, D. Vilsmeier

Summary

  • Successful beam RMS reconstruction with various machine learning models
  • Reconstruction of complete profiles with multi-layer perceptron model
    • The mapping generalizes to different beam shapes
    • Model seems to "learn" the distortion mechanisms rather than specific beam shapes
  • Model uncertainty estimates show small variations
  • These methods could potentially be used to measure sub-resolution beam profiles

Icons by icons8.

Made with Slides.com